Next Article in Journal
Green Smart Technology for Water (GST4Water): Water Loss Identification at User Level by Using Smart Metering Systems
Next Article in Special Issue
Modeling and Practice of Erosion and Sediment Transport under Change
Previous Article in Journal
An Improved Method Constructing 3D River Channel for Flood Modeling
Previous Article in Special Issue
A Shear Reynolds Number-Based Classification Method of the Nonuniform Bed Load Transport
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 11
Issue 3
10.3390/w11030404
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Modelling of Soil Erosion and Accumulation in an Agricultural Landscape—A Comparison of Selected Approaches Applied at the Small Stream Basin Level in the Czech Republic

by
Jiří Jakubínský
1,*,
Vilém Pechanec
2,
Jan Procházka
2 and
Pavel Cudlín
1
1
Global Change Research Institute CAS, Bělidla 986/4a, 603 00 Brno, Czech Republic
2
Department of Geoinformatics, Palacký University Olomouc, 17. listopadu 50, 771 46 Olomouc, Czech Republic
*
Author to whom correspondence should be addressed.
Water 2019, 11(3), 404; https://doi.org/10.3390/w11030404
Submission received: 28 December 2018 / Revised: 18 February 2019 / Accepted: 20 February 2019 / Published: 26 February 2019
(This article belongs to the Special Issue Modeling and Practice of Erosion and Sediment Transport under Change)
Browse Figures
Versions Notes

Abstract

:
This article deals with the modelling of erosion and accumulation processes in the contemporary cultural landscape of Central Europe. The area of interest is the headwater part of the small stream catchment—the Kopaninský Stream in central Czech Republic. It is an agricultural and forest–agricultural landscape with a relatively rugged topography and riverbed slope, which makes the terrain very vulnerable to water erosion. The main aim of this article is to compare the results of four selected soil erosion and sediment delivery models, which are currently widely used to quantitate the soil erosion and sediment accumulation rates, respectively. The models WaTEM/SEDEM, USPED, InVEST and TerrSet work on several different algorithms. The model outputs are compared in terms of the total volume of eroded and accumulated sediment within the catchment per time unit, and further according to the spatial distribution of sites susceptible to soil loss or sediment accumulation. Although each model is based partly on a specific calculation algorithm and has different data pre-processing requirements, we have achieved relatively comparable results in calculating the average annual soil loss and accumulation. However, each model is distinct in identifying the spatial distribution of specific locations prone to soil loss or accumulation processes.

Graphical Abstract

1. Introduction

Soil erosion is a physical process occurring almost everywhere in the world, even in landscapes with low slopes. Its main cause is, in addition to natural terrain properties, the character of the soil substrate and local climatic conditions, especially the prevailing land-use type and intensity of the anthropogenic pressure to which the given landscape is subjected. According to Pimentel [1], about 10 million hectares of fertile land are eroded each year, and about 115 million hectares of soil are affected by erosion in Europe [2]. Generally, this topic has been dealt with in the long term by both the professional community and political decision makers – as evidenced by the fact that soil erosion, as the main soil degradation process, has been identified as a key priority within the Soil Thematic Strategy of the European Commission [3]. In Europe, a number of research projects have been carried out in the past focusing on soil erosion and its modelling, and the importance of the theme is also illustrated by the fact that the European Soil Data Centre (ESDAC) was established within the Joint Research Centre in Ispra, Italy [4].
It is obvious that humans—as the initiators of soil loss, increasing the susceptibility of the soil to erosion—act directly through specific anthropogenic influences most often connected with land-use changes, as well as indirectly, usually in connection with the impacts of climate change, which is also conditioned by human activities to a certain extent. Indirect impacts of human activities affecting the soil erosion rates are most often manifested in the form of extreme hydrometeorological phenomena (flash floods or drought episodes). The relationship between the impacts of climate change and the soil loss potential is being given increasing attention, e.g., [5,6,7,8]. This is also closely related to the evapotranspiration rates and plant biomass production, among other factors [9]—it is a mechanism to reduce biomass production that could lead to long-term increases in soil erosion due to sparser vegetation cover [10].
When the upper layer of the soil cover is dredged from the agricultural land, there is a rapid decrease in the fertility, which leads to an obvious decrease in the yields of the crops grown there. An easily erodible soil substrate on sloping areas also presents a certain risk during significant precipitation episodes, where specific flood events in the form of debris flow (a fast-moving landslide made up of liquefied, unconsolidated, and saturated sediment mass) may occur. De Vente et al. [11] consider such debris flow an off-site effect of soil erosion. This phenomenon is manifested, for example, in the clogging of riverbeds, increased flood risk, and reduced lifetime of water reservoirs [12]. This makes soil erosion a critical problem [13] that requires holistic solutions involving physical and socioeconomic approaches. For these reasons, accurate quantification of soil loss and sediment delivery rates is very important, and information on the spatial distribution of these phenomena in a given landscape is also crucial. In addition to processes characterizing the current state, the possibility of predicting soil erosion–accumulation rates in the near future also becomes significant. Modelling of these phenomena takes into account, in particular, the expected impacts of climate change on the current cultural landscape as well as locally specific conditions that usually reflect the decision-making of regional stakeholders—usually landowners or local governments. The outlined factors influencing the prediction of soil erosion are, on the practical level, reflected through the land-use changes.
The Universal Soil Loss Equation (USLE) [14] and its more recent version, the Revised Universal Soil Loss Equation (RUSLE), revised by Renard et al. [15], are applied for the purposes of determining the volume of soil erosion almost everywhere in the world. Algorithms of a large number of soil loss and sediment delivery models and procedures are based on these equations—the models applied in this study are no exception. In the long term, soil erosion issues are highly relevant, especially in the Mediterranean region [16], which is, according to de Vente et al. [17], particularly sensitive to erosion due to its climate characterized by dry summers followed by intense autumn rainfall and often a steep topography with fragile soils. These findings illustrate the soil erosion risk maps created, for example, in Italy [18], Greece [19] or Spain [20]. Similar conditions, when the erosion–accumulation phenomena in the landscape were additionally amplified by the impacts of climate change starting in the late 1980s, were analyzed and subsequently described also in North Africa, as exemplified by Hallouz et al. [21] in a case study from Algeria. In Central European conditions, the increased susceptibility of soil to erosion is still mainly due to the use of inappropriate farming methods on sloping land, but the influence of climatic conditions and extreme hydrometeorological situations is increasing, which greatly increases the area of cultivated land with potential for higher soil erosion risk (e.g., [22,23,24]). The choice of specific crops grown on those lands plays a key role in the erosion rate risk —in Central Europe, this issue was dealt with, e.g., by Jones et al. [25] or Lieskovský and Kenderessy [26].
In the Czech Republic, soil erosion is one of the most widespread types of soil degradation [27], with more than 50% of agricultural land at present being threatened by water erosion and more than 10% by wind erosion [28]. The modelling of erosion processes in the Czech landscape was dealt with, e.g., by Dostál et al. [29], Krása et al. [30], Van Rompaey et al. [31] or Konečná et al [32]. Although the currently used approaches allow relatively accurate identification of sites subject to erosion risk only based on modelling techniques (i.e., without the need for field measurements), there is still considerable uncertainty associated with the determination of the volume of sediment eroded. This is also evidenced by the relatively different results achieved by individual models applied to the same territory within this study. The aim of this article is to determine the main causes of the differences between four selected, commonly used soil loss and sediment delivery models. Specifically, it is a comparison of the models in terms of their ability to identify sites with the potential for soil erosion or accumulation, as well as the exact quantification of the volume of transported material within the analyzed area. Based on this information, it is possible to determine the range of the most suitable application tasks in which the models achieve the highest-quality results.

2. Materials and Methods

2.1. Case Study Area

Selected soil loss and sediment delivery models were applied to the study area located in central Czech Republic in the Bohemian‒Moravian Highlands, approximately 90 km southeast of Prague. This is the headwater area of the Kopaninský Stream (IV. order stream) with an average altitude of 565 m, with an area of 7.1 km2, diverting water to the Želivka River (the left-side tributary of the Sázava River). The exact position of the selected watershed is shown in the map in Figure 1. The area is characterized by rugged terrain and a stream from its headwater area to the final profile near Velký Rybník Village at a distance of 4.3 km, surpassing an elevation of 108 m. Long-term average discharge in the final profile (between 1991 and 2000) was 0.027 m3 s−1 [33]. The basin of the Kopaninský Stream is classified as a slightly warm and damp climatic area, characterized by an average annual temperature of 7.1 °C. In terms of precipitation totals, the study area is located in a rather drier region (average annual rainfall is 665 mm per year) under the influence of the continental climate.
The soil type is cambic hyperskeletic Leptosol, with extremely permeable shallow loamy sands. Along the streambed, there are mainly Gleysols and Pseudogleysols in terms of soil cover. From the granulometric point of view, clay soils predominate, supplemented with sandy loam along the watercourse. The catchment area is approximately half covered with forests, and the rest is agricultural land, which is prone to erosion due to the relatively rugged relief (see Figure 2). The erosive potential is increased by the fact that these are compact and large-scale blocks of soil cover, without fragmentation made by line vegetation cover, etc. When evaluating the vegetation cover, the most common are the “distance to nature habitats” and “alien habitats,” which together cover approximately 660 hectares. Selected hydrometeorological and geomorphological characteristics of the area, important also because of their influence on the formation of rainfall‒runoff processes in the landscape, are given in Table 1. For the catchment, an agricultural‒forest landscape is typical, with approximately 50% of forest stands—these are mainly coniferous forest with an area of nearly 260 hectares. The rest of the territory comprises non-irrigated arable land and also land principally occupied by agriculture, with significant areas of natural vegetation. The composition of agricultural crops corresponds to natural conditions. Grains and oilseed rape predominate; there is also a significant proportion of maize and peas, and some root crops.

2.2. Data Sources

The quality of soil loss and sediment accumulation model outputs is directly dependent on the spatial resolution of the topography used in the form of the digital elevation model (DEM). In particular, the identification of sites with significant terrain slope and their extent, as well as the selection of various relief microforms that can influence the drainage processes at a given river basin by their morphometry, are very important. Often, these are anthropogenic forms of relief, such as road and rail embankments, flood levees, various water passes and other forms of relief, which, moreover, often occur in an agricultural landscape. However, the location and spatial extent of these forms are now relatively easy and reliably identifiable due to the high accuracy of commonly available terrain models based on the application of modern Earth remote sensing methods (e.g., LIDAR). This study used the digital elevation model of the Czech Republic of the 5th generation (DEM 5G) with a spatial resolution of 5 × 5 m and an average height error of 0.18 m in the exposed terrain and 0.30 m in forest terrain. The model was created from data acquired by airborne laser scanning in 2009–2013 and the resulting data are provided by the Czech Office for Surveying, Mapping and Cadastre (COSMC). DEM is the basic input layer of all soil loss and sediment delivery models based on the USLE equation. Based on these altitudinal data, the slope length and steepness factor (LS factor) can be estimated, which is one of the most important input parameters affecting the results of erosion process calculations. All models used work with a DEM in the form of a raster file.
Another key input for erosion–accumulation models is the data on the nature of prevailing land-use types. In this study, data from the ZABAGED® dataset (COSMC), supplemented by data from the Land Parcel Identification System (LPIS), and subsequently verified on the basis of the current aerial images of the catchment and its field survey, were used for the purposes of characterizing the landscape coverage. The land cover was categorized based on the requirements of individual models applied in this study—because of different working requirements, each model worked with a different number of land-use categories. The values of the individual factors of the USLE equation are also crucial inputs of the models—they are commonly used in its basic (USLE) or revised form (RUSLE) for determining the vulnerability of agricultural soils to water erosion. This approach is given by the following equation [14]:
A = R × K × LS × C × P,
where A is the long-term average annual soil loss [t ha−1 year−1]; R is a rainfall erosivity factor expressed in terms of kinetic energy, total precipitations and intensity of high precipitations; K represents the soil erodibility factor expressed depending on the texture and structure of soil, organic matter content in the regolith layer and permeability of the soil profile; LS is the topographic factor expressing the effect of uninterrupted slopes and steepness on soil loss amount; C is cover and the management factor expressed depending on the state of vegetation cover and agricultural technologies used; and P represents the support practice factor.
These parameters are given in the form of raster files and in some cases as constant values for the entire area of interest. All models used in the study work on the basis of the RUSLE equation, but some parameters are not applicable for the conditions of the Czech Republic according to the RUSLE methodology because of a lack of data. The equations used are therefore a combination of RUSLE and USLE approaches. The specific values used for the individual equation factors and their sources are presented in Table 2. The spatial distribution of some factors (i.e., K, LS and C factor) within the basin is shown in the maps in Figure 3.

2.3. Approaches Used to Soil Loss and Sediment Accumulation Modelling

The following paragraphs provide basic information on the individual models applied within this article. However, this is not a detailed description of the algorithms and equations on which the models are based; this information is contained in the original studies published by authors of the given models or in the cited articles, the authors of which have also applied the models in practice. For the purposes of this study we selected a total of four models, which can be categorized as soil loss and sediment delivery models according to their official descriptions. According to available documentation, each model uses the (R)USLE equation parameters to calculate the soil loss amounts and other different algorithms to calculate the soil accumulation. In all the models applied, this is the basic USLE equation (see Equation (1)), which determines the potential soil loss from the area of 1 ha per year (it means the long-term average value valid at each site of the river basin). The USLE equation is modified for use in the GIS environment by replacing the “L” and “S” factors by the combined topographic “LS” factor derived directly from the digital elevation model. Modification of the “R” factor is not applicable here because all models consistently expect a direct input of the rainfall erosivity value, not a sub-calculation of the rain erosion efficiency based on meteorological measurements. For ease of comparison, the support practice factor “P” is not considered, the value 1 is explicitly used. An overview of the models used, their selected parameters and input data requirements is provided in the Table 3.

2.3.1. InVEST

InVEST is a large set of open-source tools (models) designed to map and evaluate ecosystems and natural processes. There is a wide range of tools such as models for carbon modelling, crop pollination modelling, sediment transport modelling, but also even for fisheries or recreation modelling. The individual tools are installed in the form of one package, but each is started separately. InVEST is developed within the Natural Capital Project, which is based on a partnership between several of the world’s leading academic institutions—Stanford University, the Chinese Academy of Sciences, the University of Minnesota, The Nature Conservancy and the World Wildlife Fund. InVEST is one of the few in the range of used models to be further developed [36]. Earlier versions of the entire InVEST package are also implemented in TerrSet model as an Ecosystem Service Modeler tool.
Outputs from the sediment transport model include the sediment load delivered to the stream at an annual time scale (i.e., “sediment accumulation”), as well as the amount of sediment eroded in the catchment and retained by vegetation and topographic features. The sediment delivery module (used for computation of the sediment accumulation amount) is a spatially explicit model working at the spatial resolution of the input digital elevation model raster. For each pixel, the model first computes the amount of annual soil loss from that pixel, and then computes the sediment delivery ratio (SDR), which is the proportion of soil loss actually reaching the stream. Once sediment reaches the stream, we assume that it ends up at the catchment outlet, thus no in-stream processes are modelled. This approach was proposed by Borselli et al. [37] and has received increasing interest in recent years [38,39,40]. The amount of annual soil loss on pixel is given by the revised universal soil loss equation (RUSLE).
Based on the work by Borselli et al. [37], the model first computes the connectivity index (IC) for each pixel. The connectivity index describes the hydrological linkage between sources of sediment (from the landscape) and sinks (like streams). Higher values of IC indicate that source erosion is more likely to make it to a sink (i.e., is more connected), which happens, for example, when there is sparse vegetation or higher slope. Lower values of IC (i.e., lower connectivity) are associated with more vegetated areas and lower slopes. The sediment delivery ratio for a pixel is then derived based on the connectivity index IC, maximum theoretical SDR and calibration parameters, defining the shape of the SDR-IC relationship (which is an increasing function). The value of sediment transport from a pixel is the amount of sediment eroded from that pixel that actually reaches the stream [38].

2.3.2. USPED

USPED (Unit Stream Power-Based Erosion/Deposition Model) is a two-dimensional model of erosion and accumulation based on the RUSLE equation. This model is oriented to the spatial distribution of areas with topographical potential for soil erosion and accumulation. The model was developed in the USA in collaboration with experts from the U.S. Army Construction Engineering Laboratories, Illinois Natural History Survey, and the Faculty of Science of Comenius University in Bratislava, Slovakia. The first results were obtained by using this model in Central Illinois and Yakima Ridge, Washington, USA [41]. USPED has been applied to the basins of various scales in the USA [42] and in Italy [43,44]. Unlike the one-dimensional revised universal soil loss equation (RUSLE) models, which assume erosion mainly depends on rainfall detachment capacity, USPED model assumes that soil erosion and accumulation mainly depend on the sediment transport capacity of the surface runoff. If soil particles are already detached by rain, but there is not enough runoff to transport the soil particles because of the terrain shape or vegetation effect, the actual amount of erosion will be significantly reduced. The total surface runoff through a given pixel determines the sediment transport capacity of this area. USPED assumes that both surface runoff and sediment transport are continuous variables. The net erosion/accumulation of sediment can be positive, indicating soil deposition, or negative, indicating soil loss. The sediment transport capacity calculation is approximated using a static sediment flow rate.
In the Central European conditions, the model was used, for example, in a Slovak study by Dotterweich et al. [45] or in the Czech Republic by Bek [46] or more recently by Vysloužilová and Kliment [47]. The major advantage of the USPED model is that it does not require the installation of any special software and can be easily implemented in common GIS environments. Generally, there are a number of interrelated raster data operations that were implemented in ESRI ArcGIS 10.2 (using Raster Calculator and Spatial Analyst Tools). The result is a raster file (the size of the grid corresponding to the input data parameters) giving information about the nature of the phenomena prevailing in each cell of the given raster—positive values indicate predominant sediment delivery and negative values indicate soil loss. A detailed procedure for implementing the USPED model is described in [47] or [43].

2.3.3. TerrSet

TerrSet is commercial raster-based software that includes a large number of individual modelling tools. It also includes tools for modelling the impacts of climate change, and integrates a whole set of InVEST models (older versions of tools) or tools for processing of the remote sensing data. The software is developed and distributed by Clark Labs at Clark University in Worcester, MA, USA [48]. The calculation of soil loss and sediment accumulation was done using the RUSLE model combination, followed by the SEDIMENTATION tool from the IDRISI GIS Analysis tool kit. The main differences from other software are based on the fact that the actual calculation is performed on raster data, but all the analyses take place on the most homogeneous surfaces, the parameters of which are chosen when starting the RUSLE model and are viewed as mutually isolated patches.
According to Clark Labs [48] the SEDIMENTATION tool utilizes patch-level output from the RUSLE modelling tool to evaluate the net soil movement (erosion or deposition) within patches. The Sediment Delivery Ratio (SDR) is determined from the average annual sediment yield. Sediment yield (as in the case of InVEST model) is the amount of soil loss (erosion) that reaches a stream and is transported within the waterway. Determining net erosion or deposition begins with the total soil loss by patch produced from the RUSLE module. To determine net soil loss or deposition in each patch, SEDIMENTATION tool first determines the average elevation for each patch. Then the highest elevation in the river basin or the highest elevation in each field is located. The direction of movement of the soil is then established by the relative elevation differences between contiguous patches. Movement is always in the downslope direction. The amount of soil loss that moves into the surrounding lower patches is proportional to the length of the common boundary between the higher patch and the lower patches. Next, the net soil loss or soil accumulation in all lower patches is calculated as follows. Using the output from RUSLE, the proportional soil loss for the higher patch is compared to the soil loss for the lower patch. The difference between the amounts of soil loss from the higher patch to the lower patch represents the net soil loss or accumulation in the lower patch.

2.3.4. WaTEM/SEDEM

WaTEM/SEDEM is a specific tool developed at KU Leuven in Belgium, designed for modelling soil erosion and transport processes. The software is freely distributed and is based on the IDRISI GIS analysis tool and also uses its RST file format, which is related to the need to convert input data. The model can be used to determine soil loss and accumulation values due to water erosion, to identify areas of agricultural land susceptible to water erosion processes or to simulate the effects of different soil conservation scenarios [49,50]. The water erosion component of WaTEM/SEDEM uses an adapted version of the Revised Universal Soil loss equation (RUSLE) to calculate mean annual soil loss values. Runoff patterns are calculated with a flow algorithm that takes into account field borders, tillage direction and road infrastructure. Sediment is routed along these flow paths to the nearest river using a transport capacity term that is proportional to the potential rill erosion rate. The boundaries of the land and the topology of the river network are taken into account, which makes it suitable for modelling larger river basins.
The sediment production values do not correspond with erosion values as calculated with RUSLE, the latter being higher. RUSLE only predicts soil loss per pixel, not sediment deposition. On pixels where sediment deposition is lower than RUSLE erosion, netto erosion will be the case. It is the latter value which is used to calculate sediment production (soil accumulation). If sediment accumulation is higher than RUSLE soil loss, there will be netto sediment accumulation and this value will be used to calculate the catchment’s total sediment accumulation value. This model uses the R, K, C and P factors of the RUSLE equation. The topographical L and S factors are automatically calculated from the DEM. In order to adapt the RUSLE to a two-dimensional landscape, the upslope length is replaced by the unit contributing area, i.e., the upslope drainage per unit of contour length. The use of contributing areas implies that the effects of flow convergence and divergence on topographically complex landscapes are explicitly accounted for [51].
The erosion rate is considered equal to the sum of the potential erosion unless the local transport capacity is exceeded. The transport capacity coefficient describes the proportionality between the potential for rill erosion and the transport capacity of the overland flow. The transport capacity is the maximum sediment mass that can be transported by the overland flow. If the sediment production is higher than this transport capacity, sediment will be deposited. Thus, the higher the transport capacity coefficient, the more sediment can be transported downslope. For each land use type, transport capacity can be different. The transport capacity on a given slope segment was considered to be directly proportional to the erosion potential. If the sediment inflow exceeds the transport capacity, deposition occurs, so that the amount of material equals the transport capacity. WaTEM/SEDEM version 2004, launched through the 2006 version, is used in this study, which brings together all available versions of the given software and corrects some of their errors. The algorithms used are listed in the program manual [52]. This software generally belongs to relatively frequently used tools—in Central Europe, its outputs were presented, for example, by Bezak et al. [53] or in the Czech Republic by Van Rompaey et al. [31] and by Krása [54], which describes in more detail the individual algorithms of the model.

3. Results

3.1. Analysis of Soil Loss Caused by Water Erosion

Selected models were applied within the area of interest to determine the soil loss amount caused by water erosion. Each model works on a slightly different principle of soil loss estimation. The WaTEM/SEDEM (W/S) model calculates the “netto erosion” (the results range from negative values indicating soil erosion to positive values that represent the sediment accumulation). This principle is also applied within the USPED model. The InVEST model provides results in the form of “average erosion,” which can be understood as a direct output from the USLE equation (the results range from zero to positive values that represent soil loss). In contrast, the TerrSet model calculates both of these options (“netto erosion” and “average erosion”). Comparison of the results of the four used models in terms of spatial distribution of erodible sites within the catchment is provided by the maps in Figure 4 and Figure 5. From these outputs, a different principle of calculation is again evident—whereas the TerrSet model refers to the soil erosion amounts on individual patches corresponding to the sites with a homogeneous land-use type (the basic spatial unit is therefore a unitary land-use category), the W/S predicts the resulting soil erosion in a resolution corresponding to the extent of the input data, i.e., individual pixels with an area of 100 m2. On the same principle as W/S, other applied models also work. For this reason, TerrSet’s results may be somewhat less accurate in terms of identifying specific sites with the potential to soil loss. It can be concluded that in terms of spatial distribution, comparable results are achieved in particular by InVEST and TerrSet model, which identify almost identical sites, but differ in the estimated soil erosion volumes slightly (with total soil loss in the whole basin ranging from 43.8 to 55.4 tonnes per year). In the case of the USPED model, it is obvious that, as well as sediment accumulation modelling, soil loss volumes are significantly higher than in the case of other models, although significant soil erosion is expected in only a few localities within the catchment. When comparing the results of all four applied models, we can conclude that the models differ especially in terms of the total soil erosion volumes expected throughout the catchment—the values vary from 42.0 to 76.0 tonnes per year. This variance is largely influenced by the different area of the sites with soil erosion potential (see Table 4), which is also the result of a different approach to the areas where soil erosion and sediment accumulation were not identified. While W/S assigns a “0” value and includes these areas in following calculations, all other models assigns a “No data” attribute to that territory and do not work with it in any further steps. The difference in the number of pixels included in the calculations for each model is a key factor affecting the overall results.
The calculated soil loss values and the respective areas of the sites where the erosion takes place are shown in the graph in Figure 6. In principle, this figure captures the dependence between the number of pixels and the corresponding soil erosion values of each output raster file. The resulting chart points to the fact that in terms of the nature of the relationship between the two variables studied, there are significant differences between the models applied. The W/S model achieves the lowest soil losses, with the values found in areas ranging from 0.01 ha to almost 10 hectares (according to the number of pixels with given values).
Relatively similar results are achieved by the InVEST model, which has slightly increased soil loss values and pixels with very low erosion values are not present in such amount as compared to W/S. The curve pattern of the InVEST model outputs indicates that there is almost the same number of pixels with heterogeneous values of soil loss. A similar situation with slightly higher values (with an area covering of about 3 ha) is also the case for the USPED model. Significantly different values that occur in the TerrSet model output are mainly due to the fact that the model works with larger patches characterized by a homogeneous and higher average value.

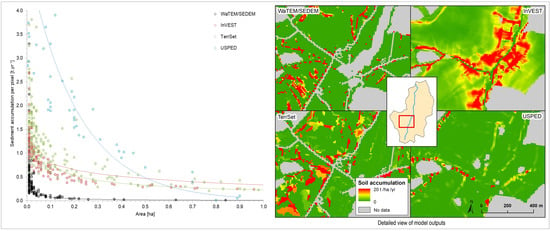
3.2. Analysis of Sediment Accumulation as a Consequence of Soil Loss by Water Erosion

In addition to the soil erosion, all of the applied models also allow the computation of sediment accumulation, and since the study area is a coherent catchment (its upper part)—a hydrologically correctly defined spatial unit—the volume of sediments should correlate with the amount of eroded material to some extent (taking into account that part of the sediment volume is transported outside the area of interest through the closing profile).
Each model has achieved relatively different results not only in terms of total volumes of the sediment accumulation (Table 5), but also when comparing the spatial distribution of the observed phenomenon (Figure 7 and Figure 8). The outputs of all the models have been unified for ease of interpretation in terms of the sediment accumulation amounts displayed, ranging from 0 to 20 tonnes per hectare per year. Although it is not obvious from map visualization, the highest values of sediment accumulation in the study area are predicted by the USPED model, which assumes soil accumulation of more than 0.11 tonnes per hectare per year. The main reason is the accumulation of extremely high amounts in the small area, which roughly corresponds to the results of the other models applied. In terms of total soil accumulation in the basin, the results of the InVEST and TerrSet models are relatively similar. However, since InVEST assumes sedimentation on a much larger area, it is clear from the comparison of average sedimentation (tonnes per hectare per year) that the outputs for InVEST and USPED are more comparable.
Based on the spatial pattern of soil accumulation values, a slightly different calculation algorithm is also apparent when comparing the three models—InVEST, USPED (in Figure 7) and WaTEM/SEDEM (on the right in Figure 8) with the TerrSet model outputs (on the left in Figure 8). While these three models counts soil accumulation (as well as soil loss) in each pixel alone and do not communicate with their surroundings (“per pixel” method), the remaining TerrSet model counts using “per patch” method. This means that at the beginning the area is divided into patches, defined on the basis of the homogeneous terrain properties and landscape cover. This approach creates a group of adjacent pixels that together make up one area in which the calculation takes place. The maximum length of drainage path is given by the user’s value or by landscape elements interrupting the drainage path. Individual patches communicate with each other, which mean that they are receiving information about computed values in adjacent areas. This aspect has a significant effect on the L factor (slope length factor), since in the case of patches the uninterrupted length of drainage path is much larger compared to the size of the per pixel models (i.e., the length of the drainage line in each pixel is always the same).
When assessing the spatial distribution of the sediment accumulation capacity of the catchment, it is obvious that large sediment accumulation-prone areas are predicted, especially by the InVEST and TerrSet model, which expects the sediment accumulation to occur at the foot of practically all slopes (this is also reflected in the sediment accumulation area, achieving the highest extent from all the models in case of the InVEST). However, based on the data in Table 5, it is evident that InVEST identifies large areas susceptible to sediment accumulation, but at the same time the model assigns relatively low values to those sites, compared to other models (up to 269 tonnes/hectare/year). By comparing the graphical outputs of all models, the influence of a different calculation algorithm is obvious. While the second pair of models (Figure 8) shows that the key factor for the prediction of the spatial distribution of sediment accumulation is the nature of land-use (the individual areas identified correspond to the extent and boundary position of the land-use units), for the first pair of models (Figure 7) the terrain characteristics play a crucial role—topography is projected onto the results, especially in the case of the InVEST model. Specific to the InVEST and USPED models, the calculation is also carried out on road surfaces, which the TerrSet and WaTEM/SEDEM models exclude from the calculation.
The above-described differences in the results of the analyzed models are evident, especially in the detailed view of the graphical outputs, showing the spatial distribution of the observed phenomena (Figure 9). The W/S model attribute high sediment accumulation values to only a few relatively small areas and minimal accumulation values that are homogeneous on a relatively large area. In contrast, the InVEST model allows for much more extensive areas, characterized by increased, but not extreme, sediment accumulation. From the anthropogenically conditioned forms of relief, the road network plays a very important role in soil erosion and sediment accumulation modelling. This element influences the results of the models by modifying the morphological parameters of the terrain, which is then reflected in input data for modelling (DEM), but also in the manner in which a given model processes this type of landscape cover. The TerrSet and WaTEM/SEDEM models used exclude the road network from calculation (they gave the “No data” attribute to the pixels), which is reflected especially when comparing the average sediment accumulation or soil loss for the whole catchment area—each model therefore calculates with a little different area affected by the number of pixels with the “No data” attribute.
For the efficient interpretation of differences in the results of the analyzed models, graph (Figure 10) was created. The graph show the course of the dependencies between the amount of sediment accumulation (i.e., soil accumulation per an area of one hectare) and an area that is characterized by given specific soil accumulation capabilities. Based on Figure 10 it is obvious that the analyzed models have different results in terms of their quality. From the distribution of values within the correlation plot, it can be stated that the greatest differences is observed between the W/S and the USPED model, where W/S assigns a large number of pixels with very low soil accumulation values, the USPED assumes the occurrence of pixels with significantly higher values. The TerrSet and InVEST models have a very similar distribution of values within the correlation plot.

4. Discussion and Conclusions

Based on the application of the four soil loss and sediment accumulation models on a selected small stream catchment in a typical Central European landscape, it can be stated that there are obvious differences between their outputs, both in terms of the total expected soil erosion and sedimentation volumes and spatial distribution of these phenomena within the catchment. Different model results, however, cannot be considered as a symptom of a certain error in the processing, but rather as a result of different algorithms and approaches used to process the input data (which were otherwise identical for each model). One of the main causes of differences in the results is the fact that each model actually works with a different number of pixels within the used raster files. This fact is dependent on different approaches to the classification of the land cover, for example, the W/S model also includes areas where there is no soil erosion (assigns a “0” value), whereas the other applied models refer to these areas as “No data” and exclude them. Furthermore, the TerrSetand W/S models also earmark the road network from the final calculation. This different fragmentation of the study area and the continuity of individual patches are key factors influencing the resulting soil erosion and sediment deposition values, respectively. Another factor influencing soil loss values is the runoff algorithm (flow accumulation algorithm) used—while W/S and TerrSet use the “Multiple Flow Direction” algorithm, USPED and InVEST have only a “Single Flow Direction” mechanism integrated. The details about their differences and influences on the runoff values are described in Wolock and McCabe [55].
Apart from the above-described differences between the results of each modelling process and its probable causes, it is also necessary to take into account the data input quality, which can greatly influence the overall accuracy of the results. It is mainly the spatial and temporal uncertainty of the input data that affects the quality of the result. An example is the “cover and management factor” (C factor), where the same value for each crop for the whole year was applied to all the models. These values are based on widely used tabular reports valid for the territory of the Czech Republic [34]. A similar principle is often used in other European countries. However, it is evident that the use of a single C factor value is largely inaccurate, especially in regions with alternating seasons, as it fluctuates during the course of the year, depending on the actual growth phase of vegetation. Much more accurate results that could subsequently be used for other decision-making processes in a given area can be achieved by determining the C factor value by means of a series of several soil erosion partial calculations, for different conditions, depending on a particular growing season (for more information on this issue, see Pechanec et al. [56]). However, to assess the quality of model outputs, the use of a single value is sufficient, especially with regard to the necessity of affecting the differences in the actual soil loss or sediment delivery calculation algorithm, not in the quality of input data.
The models used can be further compared according to their user requirements and input data requirements—in this regard, the InVEST model is probably the most user-friendly. It has a relatively purely processed user interface and has the lowest input and pre-processing requirements. The WaTEM/SEDEM model offers a fairly good user interface, but the need for high-quality input data and its pre-processing is considerable. Additionally, the need to work with data in IDRISI format can now be considered as a certain disadvantage. In contrast, the USPED model does not have any custom interface—it is essentially a series of calculations (mathematical operations with raster files) that can be done in any GIS software. Overall, this approach can be considered relatively easy; however, due to the large number of intermediate stages, it is a rather time-consuming process. The advantages and disadvantages of all analyzed models with respect to their practical applicability are summarized in Table 6.
Another possibility to evaluate the quality of the outputs of individual models is offered based on their comparison with real soil erosion values, observed and measured in the field directly within the area of interest. Since the field measurement process of soil loss is a relatively demanding issue, it is not always possible to perform such a comparison and thus verify the results of model simulations. The advantage of the area studied in this article is the fact that it is a long-term observation area, which has been investigated in the past by a number of other Czech authors (i.e., Doležal et al. [57] or Fučík et al. [58]—among other measurements, soil erosion has been measured over a certain time period. Pavlík et al. [59] carried out field measurements in the Kopaninský Stream catchment in 2005 and 2006 and found out that the average annual soil erosion amounts vary in the range between 3.4 and 4.4 t ha−1 year−1. According to the Czech Hydrometeorological Institute (CHMI) in the area of interest the average annual precipitation amounts recorded in these years (2005 and 2006) were 798 resp. 826 mm, which is a significantly above-average state (long-term average annual value is 665 mm year−1). The outputs can also be compared with the study realized by Panagos et al [8], which predicts a soil erosion of approximately 1.0–8.9 t ha−1 year−1 in the soil erosion map of Europe and soil database (ESDAC) for the given area of interest. Based on these results, it is evident that most models applied achieve highly underestimated values when compared with the outputs mentioned.
However, it is very important to emphasize that the comparison of the model outputs with the real values obtained by field measurements is only for the idea of how much the model outputs can differ from the real situation. But it is not possible to consider the models as inoperative because of the differences, as the main reason for these differences is the fact that the models do not capture the current conditions in the locality, but only the typical average values valid for a wider area. One of the key elements affecting significantly the outputs is the choice of the C factor (cover and management factor). In this study we were used year round constant value recommended for the Czech Republic by Janeček et al. [34]. Another reason for discrepancies between model outputs and the real situation may also be the unavailability of information on the existence of possible erosion control measures in the area of interest. For this reason, a constant value of "1" for the P factor (Support practice factor) is entered into the models, but for example, in the above-mentioned comparison, we do not have any detailed information on the particular state of the erosion control measures at the site where the measurements took place in the past. An important finding from the comparison of the four selected models is that all models achieve very similar results in assessing the overall average soil loss (the values found range from 0.125 to 0.156 tonnes per hectare per year). Thus, by applying these models, relatively similar results can be obtained, but in terms of the spatial distribution of the particular soil loss or accumulation areas, the outputs can vary considerably and they cannot be used for precise identification of specific locations. For the purposes of precise identification of such soil erosion-prone areas as is required for example in landscape planning or flood protection solutions, it is appropriate to use differently designed models, described, for example, in Pechanec et al. [60].
Overall, it can be summarized that for the purposes of application tasks the InVEST model is probably the most acceptable from the four models compared within this article. This model is less demanding in terms of claims on the input data and is characterized by a relatively high-quality user interface, which makes it usable even for less experienced users. The USPED model is also easy to apply, but the ease lies mainly in the fact that it is a sequence of operations feasible in any GIS software, therefore the steps are clear and the user can easily verify the quality of the partial results. The opposite is the W/S model, which works in the form of a black box (the user does not see the algorithms of the individual calculations) and the input data need to be entered in a specified format. However, all the models applied are characterized by the demands on a certain user experience in the field of environmental modelling and, in particular, the availability of the most accurate data, which completely determines the quality of the outputs.

Author Contributions

J.J. wrote the main paper and performed the USPED model computations. V.P. and J.P. performed the remaining model computations. V.P. also discussed the results and commented on the manuscript at all stages. P.C. discussed the results and commented on the manuscript in its initial phase.

Funding

This study was supported by the Ministry of Education, Youth and Sports of CR within the National Sustainability Program I (NPU I), grant number LO1415 and also by the project “LAND4FLOOD: Natural Flood Retention on Private Land”, grant number LTC18025 and project “Small watercourses and riparian ecosystem management to mitigate the impacts of environmental change (SMART2Envi),” grant number LTC18069.

Acknowledgments

The authors would like to thank Ing. Petr Fučík, Ph.D. for his initial idea to carry out this type of research in the given area of interest and also to Ing. Ondřej Cudlín, Ph.D. for providing photos from the area of interest shown in the article.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Pimentel, D. Soil erosion: A food and environmental threat. Environ. Dev. Sustain. 2006, 8, 119–137. [Google Scholar] [CrossRef]
  2. Kibblewhite, M.G.; Miko, L.; Montanarella, L. Legal frameworks for soil protection: Current development and technical information requirements. Curr. Opin. Environ. Sustain. 2012, 4, 573–577. [Google Scholar] [CrossRef]
  3. Communication from the Commission to the Council, the European Parliament, the European Economic and Social Committee and the Committee of the Regions—Thematic Strategy for Soil Protection. Brussels 2006. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX:52006DC0231 (accessed on 17 November 2018).
  4. Panagos, P.; Van Liedekerke, M.; Jones, A.; Montanarella, L. European Soil Data Centre (ESDAC): Response to European policy support and public data requirements. Land Use Policy 2012, 29, 329–338. [Google Scholar] [CrossRef]
  5. Morgan, R.P.C.; Quinton, J.N. Erosion modeling. In Landscape Erosion and Evolution Modeling; Springer: Boston, MA, USA, 2001; pp. 117–143. [Google Scholar]
  6. Nunes, J.P.; Seixas, J.; Pacheco, N.R. Vulnerability of water resources, vegetation productivity and soil erosion to climate change in Mediterranean watersheds. Hydrol. Process. Int. J. 2008, 22, 3115–3134. [Google Scholar] [CrossRef]
  7. Lorencová, E.; Frélichová, J.; Nelson, E.; Vačkář, D. Past and future impacts of land use and climate change on agricultural ecosystem services in the Czech Republic. Land Use Policy 2013, 33, 183–194. [Google Scholar] [CrossRef]
  8. Panagos, P.; Borrelli, P.; Poesen, J.; Ballabio, C.; Lugato, E.; Meusburger, K.; Montanarella, L.; Alewell, C. The new assessment of soil loss by water erosion in Europe. Environ. Sci. Policy 2015, 54, 438–447. [Google Scholar] [CrossRef] [Green Version]
  9. Nearing, M.A.; Pruski, F.F.; O’Neal, M.R. Expected climate change impacts on soil erosion rates: A review. J. Soil Water Conserv. 2004, 59, 43–50. [Google Scholar]
  10. Pruski, F.F.; Nearing, M.A. Runoff and soil-loss responses to changes in precipitation: A computer simulation study. J. Soil Water Conserv. 2002, 57, 7–16. [Google Scholar]
  11. De Vente, J.; Poesen, J.; Verstraeten, G.; Van Rompaey, A.; Govers, G. Spatially distributed modelling of soil erosion and sediment yield at regional scales in Spain. Glob. Planet. Chang. 2008, 60, 393–415. [Google Scholar] [CrossRef] [Green Version]
  12. Verstraeten, G.; Poesen, J. The nature of small-scale flooding, muddy floods and retention pond sedimentation in central Belgium. Geomorphology 1999, 29, 275–292. [Google Scholar] [CrossRef]
  13. Montgomery, D.R. Soil erosion and agricultural sustainability. Proc. Natl. Acad. Sci. USA 2007, 104, 13268–13272. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  14. Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion Losses—A Guide to Conservation Planning; Science and Education Administration, USDA: Hyattsville, MD, USA, 1978; 62p.
  15. Renard, K.G.; Foster, G.R.; Weesies, G.A.; McCool, D.K.; Yoder, D.C. Predicting Soil Erosion by Water: A Guide to Conservation Planning with the Revised Universal Soil Loss Equation (RUSLE); United States Department of Agriculture: Washington, DC, USA, 1997.
  16. Guerra, C.A.; Maes, J.; Geijzendorffer, I.; Metzger, M.J. An assessment of soil erosion prevention by vegetation in Mediterranean Europe: Current trends of ecosystem service provision. Ecol. Indic. 2016, 60, 213–222. [Google Scholar] [CrossRef] [Green Version]
  17. Grimm, M.; Jones, R.J.; Rusco, E.; Montanarella, L. Soil erosion risk in Italy: A revised USLE approach. Eur. Soil Bureau Res. Rep. 2003, 11, 23. [Google Scholar]
  18. Van Rompaey, A.; Bazzoffi, P.; Jones, R.J.; Montanarella, L. Modeling sediment yields in Italian catchments. Geomorphology 2005, 65, 157–169. [Google Scholar] [CrossRef] [Green Version]
  19. Kouli, M.; Soupios, P.; Vallianatos, F. Soil erosion prediction using the revised universal soil loss equation (RUSLE) in a GIS framework, Chania, Northwestern Crete, Greece. Environ. Geol. 2009, 57, 483–497. [Google Scholar] [CrossRef]
  20. García-Ruiz, J.M. The effects of land uses on soil erosion in Spain: A review. Catena 2010, 81, 1–11. [Google Scholar] [CrossRef]
  21. Hallouz, F.; Meddi, M.; Mahé, G.; Toumi, S.; Rahmani, S.E.A. Erosion, Suspended Sediment Transport and Sedimentation on the Wadi Mina at the Sidi M’Hamed Ben Aouda Dam, Algeria. Water 2018, 10, 895. [Google Scholar] [CrossRef]
  22. Boardman, J.; Poesen, J. Soil erosion in Europe: Major processes, causes and consequences. Soil Erosion Eur. 2006, 4, 477–487. [Google Scholar]
  23. Scholz, G.; Quinton, J.N.; Strauss, P. Soil erosion from sugar beet in Central Europe in response to climate change induced seasonal precipitation variations. Catena 2008, 72, 91–105. [Google Scholar] [CrossRef]
  24. Mullan, D. Soil erosion under the impacts of future climate change: Assessing the statistical significance of future changes and the potential on-site and off-site problems. Catena 2013, 109, 234–246. [Google Scholar] [CrossRef]
  25. Jones, R.J.; Spoor, G.; Thomasson, A.J. Vulnerability of subsoils in Europe to compaction: A preliminary analysis. Soil Tillage Res. 2003, 73, 131–143. [Google Scholar] [CrossRef]
  26. Lieskovský, J.; Kenderessy, P. Modelling the effect of vegetation cover and different tillage practices on soil erosion in vineyards: A case study in Vráble (Slovakia) using WATEM/SEDEM. Land Degrad. Dev. 2014, 25, 288–296. [Google Scholar] [CrossRef]
  27. Novotný, I. Příručka Ochrany Proti Vodní Erozi; Ministerstvo Zemědělství: Praha, Czech Republic, 2014; 73p. (In Czech)
  28. Novotný, I. Příručka Ochrany Proti Erozi Zemědělské Půdy; Ministerstvo Zemědělství a Výzkumný ÚSTAV MELIOrací a Ochrany Půdy, v.v.i.: Praha, Czech Republic, 2017; 86p. (In Czech)
  29. Dostál, T.; Krása, J.; Váška, J.; Vrána, K. The map of soil erosion hazard and sediment transport in scale of the Czech Republic. Vodní Hospodářství 2002, 52, 46–48. (In Czech) [Google Scholar]
  30. Krása, J.; Dostál, T.; Vrána, K.; Plocek, J. Predicting spatial patterns of sediment delivery and impacts of land-use scenarios on sediment transport in Czech catchments. Land Degrad. Dev. 2010, 21, 367–375. [Google Scholar] [CrossRef]
  31. Van Rompaey, A.; Krása, J.; Dostál, T. Modelling the impact of land cover changes in the Czech Republic on sediment delivery. Land Use Policy 2007, 24, 576–583. [Google Scholar] [CrossRef]
  32. Konečná, J.; Karásek, P.; Fučík, P.; Podhrázská, J.; Pochop, M.; Ryšavý, S.; Hanák, R. Integration of Soil and Water Conservation Measures in an Intensively Cultivated Watershed – A Case Study of Jihlava River Basin (Czech Republic). Europ. Countrys. 2017, 1, 17–28. [Google Scholar]
  33. Doležal, F.; Kvítek, T.; Soukup, M.; Kulhavý, Z.; Tippl, M. Czech highlands and peneplains and their hydrological role, with special regards to the Bohemo-Moravian Highland. IHP HWRP-Berichte 2004, 2, 41–56. [Google Scholar]
  34. Janeček, M. Ochrana Zemědělské Půdy Před Erozí. Metodika; Česká Zemědělská Univerzita, Fakulta Životního Prostředí: Praha, Czech Republic, 2012; 113p. (In Czech) [Google Scholar]
  35. Desmet, P.J.J.; Govers, G. A GIS procedure for automatically calculating the USLE LS factor on topographically complex landscape units. J. Soil Water Conserv. 1996, 51, 427–433. [Google Scholar]
  36. Natural Capital Project. Available online: https://www.naturalcapitalproject.org/ (accessed on 5 May 2018).
  37. Borselli, L.; Cassi, P.; Torri, D. Prolegomena to sediment and flow connectivity in the landscape: A GIS and field numerical assessment. Catena 2008, 75, 268–277. [Google Scholar] [CrossRef]
  38. Cavalli, M.; Trevisani, S.; Comiti, F.; Marchi, L. Geomorphometric assessment of spatial sediment connectivity in small Alpine catchments. Geomorphology 2013, 188, 31–41. [Google Scholar] [CrossRef]
  39. Lopez-Vicente, M.; Poesen, J.; Navas, A.; Gaspar, L. Predicting runoff and sediment connectivity and soil erosion by water for different land use scenarios in the Spanish Pre-Pyrenees. Catena 2013, 102, 62–73. [Google Scholar] [CrossRef] [Green Version]
  40. Sougnez, N.; Wesemael, B.; Van Vanacker, V. Low erosion rates measured for steep, sparsely vegetated catchments in southeast Spain. Catena 2011, 84, 1–11. [Google Scholar] [CrossRef]
  41. Mitášová, H.; Hofierka, J.; Zlocha, M.; Iverson, L.R. Modelling topographic potential for erosion and deposition using GIS. Int. J. Geogr. Inf. Syst. 1996, 10, 629–641. [Google Scholar] [Green Version]
  42. Warren, S.D.; Mitášová, H.; Hohmann, M.G.; Landsberger, S.; Iskander, F.Y.; Ruzycki, T.S.; Senseman, G.M. Validation of a 3-D enhancement of the Universal Soil Loss Equation for prediction of soil erosion and sediment deposition. Catena 2005, 64, 281–296. [Google Scholar] [CrossRef]
  43. Pistocchi, A.; Cassani, G.; Zani, O. Use of the USPED model for mapping soil erosion and managing best land conservation practices. In Proceedings of the1st International Congress on Environmental Modelling and Software, Lugano, Switzerland, 24–27 June 2002. [Google Scholar]
  44. Pelacani, S.; Märker, M.; Rodolfi, G. Simulation of soil erosion and deposition in a changing land use: A modelling approach to implement the support practice factor. Geomorphology 2008, 99, 329–340. [Google Scholar] [CrossRef]
  45. Dotterweich, M.; Stankoviansky, M.; Minár, J.; Koco, Š.; Papčo, P. Human induced soil erosion and gully system development in the Late Holocene and future perspectives on landscape evolution: The Myjava Hill Land, Slovakia. Geomorphology 2013, 201, 227–245. [Google Scholar] [CrossRef]
  46. Bek, S.; Chuman, T.; Šefrna, L. The Usability of Contours in Erosion Modelling: A Case Study on ZABAGED, Czech Republic. Acta Universitatis Carolinae 2008, 1–2, 77–86. [Google Scholar]
  47. Vysloužilová, B.; Kliment, Z. Modelování erozních a sedimentačních procesů v malém povodí. Geografie 2012, 2, 170–191. (In Czech) [Google Scholar]
  48. CLARK LABS. Available online: https://clarklabs.org/about/ (accessed on 12 May 2018).
  49. Verstraeten, G.; Van Oost, K.; Van Rompaey, A.; Poesen, J.; Govers, G. Evaluating an integrated approach to catchment management to reduce soil loss and sediment pollution through modelling. Soil Use Manag. 2002, 18, 386–394. [Google Scholar] [CrossRef]
  50. WaTEM/SEDEM Homepage. Available online: http://geo.kuleuven.be/geography/modelling/erosion/watemsedem/index.htm (accessed on 5 May 2018).
  51. Hamel, P.; Falinski, K.; Sharp, R.; Auerbach, D.A.; Sánchez-Canales, M.; Dennedy-Frank, P.J. Sediment delivery modeling in practice: Comparing the effects of watershed characteristics and data resolution across hydroclimatic regions. Sci. Total Environ. 2017, 580, 1381–1388. [Google Scholar] [CrossRef] [PubMed]
  52. Notebaert, B.; Vaes, B.; Verstraeten, G.; Govers, G. WaTEM/SEDEM Version 2006 Manual; KU Leuven, Physical and Regional Geography Research Group: Leuven, Belgium, 2006. [Google Scholar]
  53. Bezak, N.; Rusjan, S.; Petan, S.; Sodnik, J.; Mikoš, M. Estimation of soil loss by the WaTEM/SEDEM model using an automatic parameter estimation procedure. Environ. Earth Sci. 2015, 74, 5245–5261. [Google Scholar] [CrossRef]
  54. Krása, J. Hodnocení Erozních Procesů Ve Velkých Povodních za Podpory GIS. Dizertační Práce; České Vysoké Učení Technické v Praze, Fakulta Stavební, Katedra Hydromeliorací a Krajinného Inženýrství: Praha, Czech Republic, 2004; 176p. (In Czech) [Google Scholar]
  55. Wolock, D.M.; McCabe, G.J. Comparison of Single and Multiple Flow Direction Algorithms for Computing Topographic Parameters in TOPMODEL. Water Resour. Res. 1995, 5, 1315–1324. [Google Scholar] [CrossRef]
  56. Pechanec, V.; Mráz, A.; Benc, A.; Cudlín, P. Analysis of spatiotemporal variability of C-factor derived from remote sensing data. J. Appl. Remote Sens. 2018, 12, 016022. [Google Scholar] [CrossRef]
  57. Doležal, F.; Kulhavý, Z.; Kvítek, T.; Soukup, M.; Čmelík, P.; Fučík, P.; Novák, J.; Peterková, E.; Pilná, P.; Pražák, M.; et al. Hydrologický výzkum v malých zemědělských povodích. J. Hydrol. Hydromech. 2006, 54, 217–229. (In Czech) [Google Scholar]
  58. Fučík, P.; Kaplická, M.; Kvítek, T.; Peterková, J. Dynamics of Stream Water Quality during Snowmelt and Rainfall—Runoff Events in a Small Agricultural Catchment. Clean Soil Air Water 2012, 40, 154–163. [Google Scholar] [CrossRef]
  59. Pavlík, F.; Dumbrovský, M.; Podhrázská, J.; Konečná, J. The influence of water erosion processes on sediment and nutrient transport from a small agricultural catchment area. Acta Univ. Agric. Silvic. Mendel. Brun. 2012, 60, 155–165. [Google Scholar] [CrossRef]
  60. Pechanec, V.; Burian, J.; Kiliánová, H.; Němcová, Z. Geospatial analysis of the spatial conflicts of flood hazard in urban planning. Morav. Geogr. Rep. 2011, 19, 41–49. [Google Scholar]
Water 11 00404 g001 550
Figure 1. Kopaninský Stream catchment and its location within the Czech Republic.
Figure 1. Kopaninský Stream catchment and its location within the Czech Republic.
Water 11 00404 g001
Water 11 00404 g002 550
Figure 2. Typical agricultural landscape in the area of interest (photo: O. Cudlín, 2016).
Figure 2. Typical agricultural landscape in the area of interest (photo: O. Cudlín, 2016).
Water 11 00404 g002
Water 11 00404 g003 550
Figure 3. Spatial distribution of the K, LS and C factor values in the study area.
Figure 3. Spatial distribution of the K, LS and C factor values in the study area.
Water 11 00404 g003
Water 11 00404 g004 550
Figure 4. Soil loss in the study area based on the results of the InVEST and USPED models.
Figure 4. Soil loss in the study area based on the results of the InVEST and USPED models.
Water 11 00404 g004
Water 11 00404 g005 550
Figure 5. Soil loss in the study area based on the results of the TerrSet and WaTEM/SEDEM models.
Figure 5. Soil loss in the study area based on the results of the TerrSet and WaTEM/SEDEM models.
Water 11 00404 g005
Water 11 00404 g006 550
Figure 6. Relationship between the soil loss values and the corresponding number of pixels identified within the catchment where soil erosion takes place based on the results of the four models applied.
Figure 6. Relationship between the soil loss values and the corresponding number of pixels identified within the catchment where soil erosion takes place based on the results of the four models applied.
Water 11 00404 g006
Water 11 00404 g007 550
Figure 7. Sediment accumulation as a result of soil loss caused by water erosion in the study area—comparison of InVEST and USPED outputs.
Figure 7. Sediment accumulation as a result of soil loss caused by water erosion in the study area—comparison of InVEST and USPED outputs.
Water 11 00404 g007
Water 11 00404 g008 550
Figure 8. Sediment accumulation as a result of soil loss caused by water erosion in the study area—comparison of TerrSet and WaTEM/SEDEM outputs.
Figure 8. Sediment accumulation as a result of soil loss caused by water erosion in the study area—comparison of TerrSet and WaTEM/SEDEM outputs.
Water 11 00404 g008
Water 11 00404 g009 550
Figure 9. Detailed view on the selected site within the area of interest—comparison of the soil accumulation modelling results.
Figure 9. Detailed view on the selected site within the area of interest—comparison of the soil accumulation modelling results.
Water 11 00404 g009
Water 11 00404 g010 550
Figure 10. Relationship between the sediment accumulation values and the corresponding number of pixels (pixel area is 100 m2) identified within the area where the accumulation takes place based on the results of the four models applied.
Figure 10. Relationship between the sediment accumulation values and the corresponding number of pixels (pixel area is 100 m2) identified within the area where the accumulation takes place based on the results of the four models applied.
Water 11 00404 g010
Table
Table 1. Selected hydrometeorological and geomorphological characteristics of the study area.
Table 1. Selected hydrometeorological and geomorphological characteristics of the study area.
Average Annual ValuesAverage Terrain Slope (°)Average Stream Slope (°)
Precipitation (mm)Discharge in Closing Profile (m3 s−1)Specific Outflow (l.s−1 km-2)Air Temperature (°C)
665.00.0273.8027.118.32.6
Table
Table 2. Factors of the (R)USLE equation, its values and data sources used for the models applied.
Table 2. Factors of the (R)USLE equation, its values and data sources used for the models applied.
FactorFactor descriptionUsed ValuesUnitData Source
RRainfall erosivity factor40.00MJ ha−1 cm h−1Janeček et al. [34]
KSoil erodibility factor0.32–0.481t ha−1
LSTopographic factor (slope length and steepness)0.03–50.471-Own computation based on Desmet and Govers [35]
CCover and management factor0.00–0.651-Janeček et al. [34]
PSupport practice factor1.00-
1 The values of the given factor are spatially variable and the actual distribution within the area of interest is shown in Figure 3.
Table
Table 3. Selected parameters of the models applied.
Table 3. Selected parameters of the models applied.
ModelInVESTUSPEDTerrSetWaTEM/SEDEM
Basic input parametersDEMRaster fileRaster fileRaster fileRaster file
R factorRaster fileNumerical valueRaster fileNumerical value
K factorRaster fileRaster fileRaster fileRaster file or value
LS factorNumerical valueRaster fileNumerical valueNumerical value
C factorNumerical values
(for each land-use category)		Raster fileRaster fileRaster file or value
P factorNumerical valueNumerical valueRaster fileNot included
Other inputs (compulsory)River basin layer (shapefile), Biophysical parameters,
Land-use and land cover data,
Flow accumulation threshold, Calibration parameters		Not includedTerrain properties to identify areas with similar erosion rates, SDR valuesWatercourse layer (shapefile),
Land-use and land cover data,
Ptef,
Parcel Connectivity Data, Calibration parameters
Optional inputsInformation on drainage systemsCalibration parametersNo data value,
Units used,
Land fragmentation		Algorithm of LS factor computation,
Retention ponds,
Ploughing direction,
Soil roughness,
Units used
Geodata formatCommon raster file, Shapefile (.SHP),
.CSV file (biophysical parameters only)		Common raster fileIdrisi file (.RST)Idrisi file (.RST)
Table
Table 4. Comparison of the basic soil loss characteristics of the four models applied.
Table 4. Comparison of the basic soil loss characteristics of the four models applied.
Model UsedInVESTUSPEDTerrSetWaTEM/SEDEM
Total soil loss in the basin (t year−1)43.7876.0355.3841.96
Total area with soil loss (ha)349.38186.2354.77305.10
Average soil loss (t ha−1 year−1)0.0620.1070.0780.059
Table
Table 5. Comparison of the basic soil accumulation characteristics of the four models applied.
Table 5. Comparison of the basic soil accumulation characteristics of the four models applied.
Model UsedInVESTUSPEDTerrSetWaTEM/SEDEM
Total soil accumulation in the basin (t year−1)21.2480.8422.4239.86
Total area with accumulation (ha)320.58123.8793.1046.65
Average soil accumulation (t ha−1 year−1)0.0300.1140.0320.056
Table
Table 6. Rating of the models in terms of their demands on the input data and previous user experiences. “++” means the most positive rating – user-friendly model, low input data requirements, etc.; “--“ indicates the most negative rating; and 0 means that the model does not have a user interface.
Table 6. Rating of the models in terms of their demands on the input data and previous user experiences. “++” means the most positive rating – user-friendly model, low input data requirements, etc.; “--“ indicates the most negative rating; and 0 means that the model does not have a user interface.
Model UsedInVESTUSPEDTerrSetWaTEM/SEDEM
Data pre-processing requirements++-+--
User-friendly interface++0++
Claims for prior user experiences+++--
Failure sensitivity (including the difficulty of error detecting)++--

Share and Cite

MDPI and ACS Style

Jakubínský, J.; Pechanec, V.; Procházka, J.; Cudlín, P. Modelling of Soil Erosion and Accumulation in an Agricultural Landscape—A Comparison of Selected Approaches Applied at the Small Stream Basin Level in the Czech Republic. Water 2019, 11, 404. https://doi.org/10.3390/w11030404

AMA Style

Jakubínský J, Pechanec V, Procházka J, Cudlín P. Modelling of Soil Erosion and Accumulation in an Agricultural Landscape—A Comparison of Selected Approaches Applied at the Small Stream Basin Level in the Czech Republic. Water. 2019; 11(3):404. https://doi.org/10.3390/w11030404

Chicago/Turabian Style

Jakubínský, Jiří, Vilém Pechanec, Jan Procházka, and Pavel Cudlín. 2019. "Modelling of Soil Erosion and Accumulation in an Agricultural Landscape—A Comparison of Selected Approaches Applied at the Small Stream Basin Level in the Czech Republic" Water 11, no. 3: 404. https://doi.org/10.3390/w11030404

APA Style

Jakubínský, J., Pechanec, V., Procházka, J., & Cudlín, P. (2019). Modelling of Soil Erosion and Accumulation in an Agricultural Landscape—A Comparison of Selected Approaches Applied at the Small Stream Basin Level in the Czech Republic. Water, 11(3), 404. https://doi.org/10.3390/w11030404

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop