Flow Division Dynamics in the Mekong Delta: Application of a 1D-2D Coupled Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Approach
- (1)
- Studying the role of the irrigation channels:
- (a)
- For sensitivity analysis, the irrigation channels were excluded from the 1D domain to see the immediate effect on tidal propagation and prism.
- (b)
- By increasing roughness along different channels, the model was re-calibrated to quantify the irrigation system contribution to tidal propagation and prism.
- (2)
- The complete domain was then used to study cumulative freshwater distribution during the dry season.
- (3)
- Temporal variation of subtidal water level and discharge was then related to other physical processes such as wind and surge level in the sea.
- (4)
- To isolate the role of different physical processes, we exclude all the sink terms (water demand and evaporation) and zoomed in on the Hau River and its two distributaries (see Table 1 and Figure 1a). Following a method of factors separation (e.g., see Reference [29,34]), various forcings in the model were one-by-one included or excluded to examine their individual impact and their interaction with other forcings.
2.2. Model Description
2.3. Model Set Up
2.4. Time Series Analysis
2.5. Mekong Model Calibration and Validation
3. Results
3.1. Tidal Propagation and the Role of the Irrigation/Navigation System
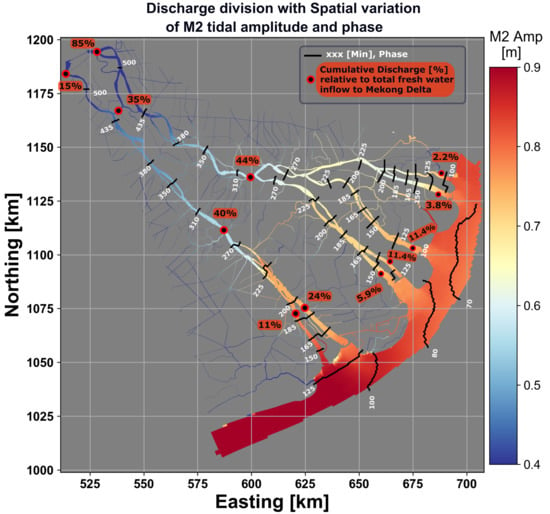
3.2. Cumulative Freshwater Distribution
3.3. Temporal Freshwater Distribution
3.4. Physical Processes and Sensitivity Analysis
4. Discussion
4.1. Effect of Primary and Secondary Channels
4.2. Temporal and Cumulative and Temporal Discharge Division
4.3. Limitations and Uncertainties
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Data Availability
References
- Anthony, E.J.; Brunier, G.; Besset, M.; Goichot, M.; Dussouillez, P.; Nguyen, V.L. Linking rapid erosion of the Mekong River delta to human activities. Sci. Rep. 2015, 5, 14745. [Google Scholar] [CrossRef]
- ICEM Mekong Delta Climate Change Forum 2009; ICEM: Seoul, Korea, 2009.
- Käkönen, M. Mekong Delta at the Crossroads: More Control or Adaptation? Ambio 2008, 37, 205–212. [Google Scholar] [CrossRef]
- GSO Statistical Handbook of Vietnam 2015; GSO: Hanoi, Vietnam, 2015.
- Mekong River Commission. Overview of the Hydrology of the Mekong Basin; Mekong River Commission: Vientiane, Laos, 2005. [Google Scholar]
- Mekong River Commission. State of the Basin Report 2010; Mekong River Commission: Vientiane, Laos, 2010. [Google Scholar]
- Syvitski, J.P.M.; Kettner, A.J.; Overeem, I.; Hutton, E.W.H.; Hannon, M.T.; Brakenridge, G.R.; Day, J.; Vörösmarty, C.; Saito, Y.; Giosan, L.; et al. Sinking deltas due to human activities. Nat. Geosci. 2009, 2, 681–686. [Google Scholar] [CrossRef]
- Smajgl, A.; Toan, T.Q.; Nhan, D.K.; Ward, J.; Trung, N.H.; Tri, L.Q.; Tri, V.P.D.; Vu, P.T. Responding to rising sea levels in the Mekong Delta. Nat. Clim. Chang. 2015, 5, 167–174. [Google Scholar] [CrossRef]
- Minderhoud, P.S.J.; Erkens, G.; Pham, V.H.; Bui, V.T.; Erban, L.; Kooi, H.; Stouthamer, E. Impacts of 25 years of groundwater extraction on subsidence in the Mekong delta, Vietnam. Environ. Res. Lett. 2017, 12, 064006. [Google Scholar] [CrossRef]
- Van, P.D.T.; Popescu, I.; Van Griensven, A.; Solomatine, D.P.; Trung, N.H.; Green, A. A study of the climate change impacts on fluvial flood propagation in the Vietnamese Mekong Delta. Hydrol. Earth Syst. Sci. 2012, 16, 4637–4649. [Google Scholar] [CrossRef]
- Kuenzer, C.; Guo, H.; Huth, J.; Leinenkugel, P.; Li, X.; Dech, S. Flood Mapping and Flood Dynamics of the Mekong Delta: ENVISAT-ASAR-WSM Based Time Series Analyses. Remote Sens. 2013, 5, 687–715. [Google Scholar] [CrossRef]
- Nguyen Van Khanh, T.; Nguyen Viet, D.; Fujii, H.; Kummu, M.; Merz, B.; Apel, H. Has dyke development in the Vietnamese Mekong Delta shifted flood hazard downstream? Hydrol. Earth Syst. Sci. 2017, 21, 3991–4010. [Google Scholar]
- ICEM Mekong Delta Central Connectivity Project: Rapid Climate Change, Threat and Vulnerability Assessment; ICEM: Seoul, Korea, 2012.
- Mekong Delta Plan, Long-Term Vision and Strategy for a Safe, Prospersous and Sustainable Delta. 2013. Available online: https://www.mekongdeltaplan.com (accessed on 19 April 2019).
- Minderhoud, P.S.J. The Sinking Mega-Delta—Present and Future Subsidence of the Vietnamese Mekong Delta; Utrecht Studies in Earth Sciences: Utrecht, The Netherlands, 2019. [Google Scholar]
- Kummu, M.; Tes, S.; Yin, S.; Adamson, P.; Józsa, J.; Koponen, J.; Richey, J.; Sarkkula, J. Water balance analysis for the Tonle Sap Lake-floodplain system. Hydrol. Process. 2014, 28, 1722–1733. [Google Scholar] [CrossRef]
- Gugliotta, M.; Saito, Y.; Nguyen, V.L.; Ta, T.K.O.; Nakashima, R.; Tamura, T.; Uehara, K.; Katsuki, K.; Yamamoto, S. Process regime, salinity, morphological, and sedimentary trends along the fluvial to marine transition zone of the mixed-energy Mekong River delta, Vietnam. Cont. Shelf Res. 2017, 147, 7–26. [Google Scholar] [CrossRef]
- Nguyen, A.D.; Savenije, H.H.G. Salt intrusion in multi-channel estuaries: A case study in the Mekong Delta, Vietnam. HESS 2006, 10, 743–754. [Google Scholar]
- Nowacki, D.J.; Ogston, A.S.; Nittrouer, C.A.; Fricke, A.T.; Van, P.D.T. Sediment dynamics in the lower Mekong River: Transition from tidal river to estuary. J. Geophys. Res. C Ocean. 2015, 120, 6363–6383. [Google Scholar] [CrossRef]
- Manh, N.V.; Dung, N.V.; Hung, N.N.; Merz, B.; Apel, H. Large-scale suspended sediment transport and sediment deposition in the Mekong Delta. Hydrol. Earth Syst. Sci. 2014, 18, 3033–3053. [Google Scholar] [CrossRef]
- Van Manh, N.; Dung, N.V.; Hung, N.N.; Kummu, M.; Merz, B.; Apel, H. Future sediment dynamics in the Mekong Delta floodplains: Impacts of hydropower development, climate change and sea level rise. Glob. Planet. Chang. 2015, 127, 22–33. [Google Scholar] [CrossRef]
- Phi Hoang, L.; Lauri, H.; Kummu, M.; Koponen, J.; Vliet, M.T.H.V.; Supit, I.; Leemans, R.; Kabat, P.; Ludwig, F. Mekong River flow and hydrological extremes under climate change. Hydrol. Earth Syst. Sci. 2016, 20, 3027–3041. [Google Scholar] [CrossRef]
- Xing, F.; Meselhe, E.A.; Allison, M.A.; Weathers, H.D. Analysis and numerical modeling of the flow and sand dynamics in the lower Song Hau channel, Mekong Delta. Cont. Shelf Res. 2017, 147, 62–77. [Google Scholar] [CrossRef]
- Thanh, V.Q.; Reyns, J.; Wackerman, C.; Eidam, E.F.; Roelvink, D. Modelling suspended sediment dynamics on the subaqueous delta of the Mekong River. Cont. Shelf Res. 2017, 147, 213–230. [Google Scholar] [CrossRef]
- Nguyen, A.D.; Savenije, H.H.G.; Pham, D.N.; Tang, D.T. Using salt intrusion measurements to determine the freshwater discharge distribution over the branches of a multi-channel estuary: The Mekong Delta case. Estuar. Coast. Shelf Sci. 2008, 77, 433–445. [Google Scholar] [CrossRef]
- Savenije, H.H.G. Salinity and Tides in Alluvial Estuaries; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Godin, G.; Martinez, A. Friction on the Propagation O F Tides in a Channel. Cont. Shelf Res. 1994, 14, 723–748. [Google Scholar] [CrossRef]
- Henrie, K.; Valle-Levinson, A. Subtidal variability in water levels inside a subtropical estuary. J. Geophys. Res. Ocean. 2014, 119, 7483–7492. [Google Scholar] [CrossRef]
- Sassi, M.G.; Hoitink, A.J.F.; De Brye, B.; Vermeulen, B.; Deleersnijder, E. Tidal impact on the division of river discharge over distributary channels in the Mahakam Delta. Ocean Dyn. 2011, 61, 2211–2228. [Google Scholar] [CrossRef]
- Wang, Z.B.; De Vries, M.; Fokkink, R.J.; Langerak, A. Stability of river bifurcations in ID morphodynamic models. J. Hydraul. Res. 1995, 33, 739–750. [Google Scholar] [CrossRef]
- Bolla Pittaluga, M.; Repetto, R.; Tubino, M. Channel bifurcation in braided rivers: Equilibrium configurations and stability. Water Resour. Res. 2003, 39, 1–13. [Google Scholar] [CrossRef]
- Ramamurthy, A.S.; Qu, J.; Vo, D. Numerical and experimental study of dividing open-channel flows. J. Hydraul. Eng. 2007, 133, 1135–1144. [Google Scholar] [CrossRef]
- Kleinhans, M.G.; Jagers, H.R.A.; Mosselman, E.; Sloff, C.J. Bifurcation dynamics and avulsion duration in meandering rivers by one-dimensional and three-dimensional models. Water Resour. Res. 2008, 44, 1–31. [Google Scholar] [CrossRef]
- Buschman, F.A.; Hoiting, A.J.F.; van der Vegt, M.; Hoekstra, P. Subtidal flow division at a shallow tidal junction. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Hidayat, H.; Vermeulen, B.; Sassi, M.G.; Torfs, P.J.J.F.; Hoitink, A.J.F. Discharge estimation in a backwater affected meandering river. Hydrol. Earth Syst. Sci. 2011, 15, 2717–2728. [Google Scholar] [CrossRef]
- Sassi, M.G.; Hoitink, A.J.F. River flow controls on tides and tide-mean water level profiles in a tidal freshwater river. J. Geophys. Res. Ocean. 2013, 118, 4139–4151. [Google Scholar] [CrossRef]
- Kernkamp, H.W.J.; Van Dam, A.; Stelling, G.S.; De Goede, E.D. Efficient scheme for the shallow water equations on unstructured grids with application to the Continental Shelf. Ocean Dyn. 2011, 61, 1175–1188. [Google Scholar] [CrossRef]
- Kramer, S.C.; Stelling, G.S. A conservative unstructured scheme for rapidly varied flows. Int. J. Numer. Methods Fluids 2008, 58, 183–212. [Google Scholar] [CrossRef]
- Arias, M.E.; Piman, T.; Lauri, H.; Cochrane, T.A.; Kummu, M. Dams on Mekong tributaries as significant contributors of hydrological alterations to the Tonle Sap Floodplain in Cambodia. Hydrol. Earth Syst. Sci. 2014, 18, 5303–5315. [Google Scholar] [CrossRef]
- Cochrane, T.A.; Arias, M.E.; Piman, T. Historical impact of water infrastructure on water levels of the Mekong River and the Tonle Sap system. Hydrol. Earth Syst. Sci. 2014, 18, 4529–4541. [Google Scholar] [CrossRef]
- Godin, G. The Analysis of Tides; University of Toronto: Toronto, ON, USA, 1972. [Google Scholar]
- Kumiko, T.; Takao, M.; Toru, M. Seasonal changes in radiation and evaporation implied from the diurnal distribution of rainfall in the Lower Mekong. Hydrol. Process. 2008, 22, 1257–1266. [Google Scholar]
- Pugh, D.; Woodworth, P. Sea-Level Science: Understanding Tides, Surges, Tsunamis and Mean Sea-Level Changes; Cambridge University Press: Cambridge, UK, 2014; ISBN 9781139898706. [Google Scholar]
- Lewis, R.E.; Lewis, J.O. The principal factors contributing to the flux of salt in a narrow, partially stratified estuary. Estuar. Coast. Shelf Sci. 1983, 16, 599–626. [Google Scholar] [CrossRef]
- Díez-Minguito, M.; Contreras, E.; Polo, M.J.; Losada, M.A. Spatio-temporal distribution, along-channel transport, and post-riverflood recovery of salinity in the Guadalquivir estuary (SW Spain). J. Geophys. Res. Ocean. 2013, 118, 2267–2278. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting Through Conceptual Models Part I-a Discussion of Principles*. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Dang, T.D.; Cochrane, T.A.; Arias, M.E.; Tri, V.P.D. Future hydrological alterations in the Mekong Delta under the impact of water resources development, land subsidence and sea level rise. J. Hydrol. Reg. Stud. 2018, 15, 119–133. [Google Scholar] [CrossRef]
- Chow, V.T. Open Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Ritter, A.; Muñoz-Carpena, R. Performance evaluation of hydrological models: Statistical significance for reducing subjectivity in goodness-of-fit assessments. J. Hydrol. 2013, 480, 33–45. [Google Scholar] [CrossRef]
- Dyer, K. Estuaries, a Physical Introduction, 2nd ed.; John Wiley & Sons Ltd.: New York, NY, USA, 1997; ISBN 0-471-97471-4. [Google Scholar]
- Brunier, G.; Anthony, E.J.; Goichot, M.; Provansal, M.; Dussouillez, P. Recent morphological changes in the Mekong and Bassac river channels, Mekong delta: The marked impact of river-bed mining and implications for delta destabilisation. Geomorphology 2014, 224, 177–191. [Google Scholar] [CrossRef]
- Stein, U.; Alpert, P. Factor Separation in Numerical Simulations. J. Atmos. Sci. 1993, 50, 2107–2115. [Google Scholar] [CrossRef]
- Alebregtse, N.C.; de Swart, H.E. Effect of river discharge and geometry on tides and net water transport in an estuarine network, an idealized model applied to the Yangtze Estuary. Cont. Shelf Res. 2016, 123, 29–49. [Google Scholar] [CrossRef]
- LeBlond, P.H. On tidal propagation in shallow rivers. J. Geophys. Res. 1978, 83, 4717. [Google Scholar] [CrossRef]
- Lighhill, J. Waves in Fluids; Cambridge University Press: Cambridge, UK, 1978. [Google Scholar]
- Kinsler, L.E.; Frey, A.R.; Coppens, A.B.; Sanders, J.V. Fundamentals of Acoustics, 4th ed.; John Wiley & Sons lnc.: Hoboken, NJ, USA, 2000. [Google Scholar]
- Alebregtse, N.C.; de Swart, H.E. Effect of a secondary channel on the non-linear tidal dynamics in a semi-enclosed channel: A simple model. Ocean Dyn. 2014, 64, 573–585. [Google Scholar] [CrossRef]
- Alebregtse, N.C.; de Swart, H.E.; Schuttelaars, H.M. Resonance characteristics of tides in branching channels. J. Fluid Mech. 2013, 728, 1–11. [Google Scholar] [CrossRef]
- Thi Ha, D.; Ouillon, S.; Van Vinh, G. Water and Suspended Sediment Budgets in the Lower Mekong from High-Frequency Measurements (2009–2016). Water 2018, 10, 846. [Google Scholar] [CrossRef]
- Allison, M.A.; Weathers, D.H.; Meselhe, E.A. Bottom morphology in the Song Hau distributary channel, Mekong River Delta, Vietnam. Cont. Shelf Res. 2017, 147, 51–61. [Google Scholar] [CrossRef]
- Eslami, A.S.; Trung, N.N. Water Level and Discharge Data in the Mekong Delta 2018. Available online: https://doi.org/10.5281/zenodo.1478608 (accessed on 19 April 2019).













| Study | Fraction of Song Hau Discharge | Approach | |
|---|---|---|---|
| Dinh An (DA) | Tran De (TD) | ||
| Nguyen et al. [25] | 70% | 30% | Analytical salt intrusion model [26] |
| Nowacki et al. [19] | 40% | 60% | 25-h field measurements (calculating percentage of DA+TD discharge) |
| Xing et al. [23] | 94% | 6% | 2DH numerical modeling of lower Song Hau distributary channel |
| Input data | Source | Description |
|---|---|---|
| River network, channel geometry and profile definitions | SIWRP | Mainly from 2008 and updated when possible |
| Lower Hau River bathymetry | from Nowacki et al. [19] | multiple cross-sections along Hau River and DA channel |
| 2DH model grid and bathymetry of TSL and the continental shelf | Vo et al. [24] | published in 2018 |
| Water level data within VMD | SRHMC | Hourly time-series |
| Discharge data within VMD | SRHMC | Hourly time-series |
| Water level at Cambodian stations | SIWRP | Once a day at 7:00AM |
| Discharge at Kratie | MRC | Daily averaged discharge |
| Offshore wind | Climate Forecast System Reanalysis (CSFR), originally published by NCEP NOAA downloaded from online DHI metocean data portal | The hourly wind parameters at 10 m |
| Evaporation | Literature [16,42] | Daily [mm/day], in consultation with SIWRP |
| Water demand | SIWRP | Per region [m3/s] |
| Offshore Tidal constituents | TOPEX/Poseidon global inverse tide model (TPXO 8.0) | Amplitude and phase of tidal constituents (M2, S2, N2, K2, K1, O1, P1, Q1, MF, MM, M4, MS4, MN4) |
| Obs. Stations | Correlation Coefficient (R2) | Nash-Sutcliffe Efficiency (NSE) | ||||||
|---|---|---|---|---|---|---|---|---|
| Water Level | Discharge | Water Level | Discharge | |||||
| 2010 | 2012 | 2010 | 2012 | 2010 | 2012 | 2010 | 2012 | |
| Ba Nho | 0.87 | - | 0.91 | - | 0.86 | - | 0.83 | - |
| Vam Kenh | 0.97 | 0.97 | - | - | 0.97 | 0.97 | - | - |
| Tan An | 0.82 | - | - | - | 0.82 | - | - | - |
| Chau Doc | 0.77 | 0.78 | 0.9 | 0.88 | 0.66 | 0.65 | 0.35 | 0.4 |
| Can Tho | 0.96 | 0.96 | 0.92 | 0.93 | 0.96 | 0.95 | 0.92 | 0.92 |
| My Hoa | 0.97 | - | - | - | 0.96 | - | - | - |
| An Thuan | 0.97 | 0.98 | - | - | 0.97 | 0.97 | - | - |
| My Thuan | 0.92 | 0.93 | 0.92 | 0.93 | 0.92 | 0.93 | 0.92 | 0.92 |
| Tan Chau | 0.92 | - | 0.9 | 0.91 | 0.88 | - | 0.9 | 0.9 |
| Ben Trai | 0.97 | 0.81 | - | - | 0.97 | 0.8 | - | - |
| My Tho | 0.91 | - | - | - | 0.91 | - | - | - |
| Vam Nao | 0.96 | - | 0.88 | 0.89 | 0.64 | - | 0.87 | 0.88 |
| Sim. Name | Physics Included | Outcome |
|---|---|---|
| Reference | R + T + S | N.A. |
| No Surge | R + T | Surge drives large discharge variations. |
| No River Discharge | T + S | River discharge moderates the effect of event-like wind-driven ocean surge levels |
| No Tide | R + S | Tides, along with surge, influence subtidal discharge and its division, but less significant compared to surge |
| Only Discharge | R | In absence of downstream processes (e.g., tide and surge), flow division, independent of river discharge, only depends on distributary channel properties |
| Only Surge | S | In absence of varying upstream discharge and downstream tidal forcing, discharge division depends on channel geometry (similar to Only Discharge) |
| Only Tide | T | development of a fortnightly tidal wave due to fortnightly oscillation of frictional forces |
| Study | Dinh An | Tran De | Tieu | Dai |
|---|---|---|---|---|
| Nguyen et al. [25] | 70% of Can Tho, 27.4% of total VMD freshwater inflow | 30% of Can Tho, 11.5% of total VMD freshwater inflow | 10.7% of total VMD freshwater inflow | 20.8% of total VMD freshwater inflow |
| Nowacki et al. [19] | 40% of the sum of DA and TD | 60% of the sum of DA and TD | N.A. | N.A. |
| Xing et al. [23] | 94% of Can Tho | 6% of Can Tho | N.A. | N.A. |
| Present study | 60% of Can Tho, 23.8% of total VMD freshwater inflow | 28% of Can Tho, 10.8% of total VMD freshwater inflow | 2.1% of total VMD freshwater inflow | 3.1% of total VMD freshwater inflow |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eslami, S.; Hoekstra, P.; Kernkamp, H.; Nguyen Trung, N.; Do Duc, D.; Tran Quang, T.; Februarianto, M.; Van Dam, A.; van der Vegt, M. Flow Division Dynamics in the Mekong Delta: Application of a 1D-2D Coupled Model. Water 2019, 11, 837. https://doi.org/10.3390/w11040837
Eslami S, Hoekstra P, Kernkamp H, Nguyen Trung N, Do Duc D, Tran Quang T, Februarianto M, Van Dam A, van der Vegt M. Flow Division Dynamics in the Mekong Delta: Application of a 1D-2D Coupled Model. Water. 2019; 11(4):837. https://doi.org/10.3390/w11040837
Chicago/Turabian StyleEslami, Sepehr, Piet Hoekstra, Herman Kernkamp, Nam Nguyen Trung, Dung Do Duc, Tho Tran Quang, Mochamad Februarianto, Arthur Van Dam, and Maarten van der Vegt. 2019. "Flow Division Dynamics in the Mekong Delta: Application of a 1D-2D Coupled Model" Water 11, no. 4: 837. https://doi.org/10.3390/w11040837
APA StyleEslami, S., Hoekstra, P., Kernkamp, H., Nguyen Trung, N., Do Duc, D., Tran Quang, T., Februarianto, M., Van Dam, A., & van der Vegt, M. (2019). Flow Division Dynamics in the Mekong Delta: Application of a 1D-2D Coupled Model. Water, 11(4), 837. https://doi.org/10.3390/w11040837