Copula-Based Research on the Multi-Objective Competition Mechanism in Cascade Reservoirs Optimal Operation
Abstract
:1. Introduction
2. Study Area and Data
3. Research Methodology
3.1. Description of Multi-Objective Model of the Heihe Cascade Reservoirs Operation
Objective Function
3.2. ICGC-NSGA-II Algorithm
3.3. Normalization of Objective Sequence
3.4. Copulas Theory
- Dependence measurement. Before constructing multivariate joint distribution, it is necessary to measure the correlation between different random variables according to the correlation index.
- Marginal distribution fitting. The marginal distribution of each single variable should be fitted to find the appropriate distribution type. Since all the parametric methods in this study have not passed the test, the non-parametric method is adopted here. In this paper, a non-parametric empirical frequency determination method based on the Gringorten formula [43,44] is introduced.
- Parameter estimation of copula function. In this paper, the maximum likelihood estimation method [45] is used to estimate parameters.
- Goodness of fit evaluation. The goodness-of-fit evaluation is an important way of comparing and analyzing the goodness-of-fit evaluation indices of different types of copula functions, so as to optimize the most suitable distribution of copula functions.
- 5.
- Computation of Joint Distribution Sequence Values. In order to find a new sequence that reflects the overall characteristics of the two variables, it needs to inverse the frequency sequence obtained above and then get the joint sequence value of the two variables. In this study, the inverse function, that is, NORMINV for the normal cumulative distribution function in the MATLAB software is used to derive the sequence values of the joint probability distribution of the copula function.
4. Results and Discussions
4.1. Optimal Results of the ICGC-NSGA-II
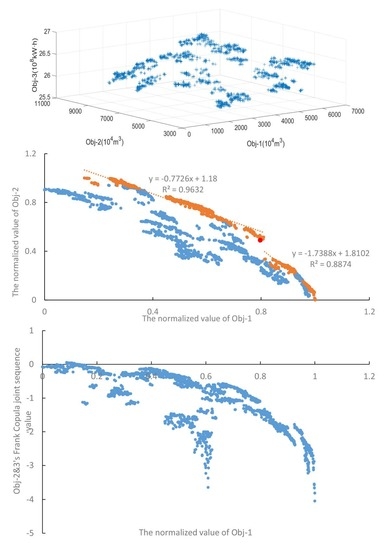
4.2. Analysis of Two-Objective Competition Mechanism
4.3. Analysis of Three-Objective Competition Mechanism
5. Conclusions
- The three-dimensional and two-dimensional spatial distributions of the Pareto solutions prove that there are mutual restrictions and influences among the three objectives. In order to avoid the disadvantage of choosing only a limited number of representative solutions and being too arbitrary, the long series of non-inferior solutions obtained are adopted to study the competition mechanism in this study. On the premise of sufficient optimization, there is a macro-rule of ’one falls another rises.’ When one objective solution is inferior, then the other two targets show the strongest regularity and optimum.
- In the analysis of the two-objective competition mechanism, the functional formulas between the sequences of two objects are given, which can quantitatively describe the relationship and interactions. It was found that when the irrigation water shortage was large, with it decreasing, the ecological water shortage increased slowly, which indicates that the two are inversely correlated. In addition, there is a positive correlation between the multi-year average irrigation water shortage and the average power generation, as there is between ecological water shortage and power generation.
- This study first applied the two-variable joint copula function to the study of the multi-objective competition mechanism. Based on the advantage that copula function cannot produce information distortion in the process of connecting the marginal distribution of two sub-sequences, a new sequence containing the comprehensive information of the two targets is generated by using the joint copula function of two variables to combine the sequence values of any two objectives and the competition mechanism between the remaining target sequence and the joint sequence of two targets is studied. A new way is provided for studying the influence of a single sequence on the compound sequence of two sequences.
- The three-objective competition mechanism infers that the competition between power generation and other objectives is the least and the change of power generation has the least influence on the other two as a whole. Specifically, the recommended annual average water shortage for irrigation is about 1492 × 104 m3. When it is less than this value, with decreasing irrigation water shortage, the overall impact of ecological water and power generation is greater. Only when the irrigation water shortage is less than 3193 × 104 m3, will there be a strong impact on other objectives. Additionally, the average annual ecological water shortage is about 4951 × 104m3, when it is less than this value, the overall impact of the irrigation water and power generation will be greater as the ecological water shortage decreases. After the average generation capacity has been more than 26.48 × 108 kW h for many years, the objective of power generation has a strong influence on the other targets.
Author Contributions
Funding
Conflicts of Interest
References
- Asvini, M.S.; Amudha, T. Design and development of bio-inspired framework for reservoir operation optimization. Adv. Water Resour. 2017, 110, 193–202. [Google Scholar] [CrossRef]
- Guan, J.; Kentel, E.; Aral, M.M. Genetic Algorithm for Constrained Optimization Models and Its Application in Groundwater Resources Management. J. Water Resour. Plan. Manag. 2008, 134, 64–72. [Google Scholar] [CrossRef]
- Mathur, Y.P.; Nikam, S.J. Optimal Reservoir Operation Policies Using Genetic Algorithm. Int. J. Eng. Technol. 2009, 1, 184–187. [Google Scholar] [CrossRef]
- Rodrigues, D.; Pereira, L.A.M.; Nakamura, R.Y.M.; Costa, K.A.P.; Yang, X.-S.; Souza, A.N.; Papa, J.P. A wrapper approach for feature selection and optimum-path forest based on bat algorithm. Expert Syst. Appl. 2014, 41, 2250–2258. [Google Scholar] [CrossRef]
- Jiang, Z.; Ji, C.; Qin, H.; Feng, Z. Multi-stage progressive optimality algorithm and its application in energy storage operation chart optimization of cascade reservoirs. Energy 2018, 148, 309–323. [Google Scholar] [CrossRef]
- Yang, T.; Hsu, K.; Duan, Q.; Sorooshian, S.; Wang, C. Method to Estimate Optimal Parameters; Springer Nature: Basingstoke, UK, 2018; pp. 1–39. [Google Scholar]
- Reddy, M.J.; Kumar, D.N. Optimal reservoir operation using multi-objective evolutionary algorithm. Water Resour. Manag. 2006, 20, 861–878. [Google Scholar]
- Tauxe, G.W.; Inman, R.R.; Mades, D.M. Multiobjective dynamic programing with application to a reservoir. Water Resour. Res. 1979, 15, 1403–1408. [Google Scholar] [CrossRef]
- Liang, Q.; Johnson, L.E.; Yu, Y.S. A Comparison of two methods for multiobjective optimization for reservoir operation 1. JAWRA J. Am. Water Resour. Assoc. 1996, 32, 333–340. [Google Scholar] [CrossRef]
- Momtahen, S.; Dariane, A.B. Direct Search Approaches Using Genetic Algorithms for Optimization of Water Reservoir Operating Policies. J. Water Resour. Plan. Manag. 2007, 133, 202–209. [Google Scholar] [CrossRef]
- Yuan, X.; Zhang, Y.; Yuan, Y. Improved self-adaptive chaotic genetic algorithm for hydrogenation scheduling. J. Water Resour. Plan. Manag. 2008, 134, 319–325. [Google Scholar] [CrossRef]
- Yang, X. A new metaheuristic bat-inspired algorithm. In Nature Inspired Cooperative Strategies for Optimization; Studies in Computational Intelligence, NISCO; Springer: Berlin/Heidelberg, Germany, 2010; Volume 284. [Google Scholar]
- Yang, T.; Gao, X.; Sellars, S.L.; Sorooshian, S. Improving the multi-objective evolutionary optimization algorithm for hydropower reservoir operations in the California Oroville–Thermalito complex. Environ. Model. Softw. 2015, 69, 262–279. [Google Scholar] [CrossRef]
- Goyal, M.K.; Ojha, C.S.P.; Singh, R.D.; Swamee, P.K.; Nema, R.K. Application of ANN, fuzzy logic and decision tree algorithms for the development of reservoir operating rules. Water Resour. Manag. 2013, 27, 911–925. [Google Scholar]
- Kim, T.; Heo, J.H.; Jeong, C.S. Multi-reservoir system optimization in the Han River basin using multi-objective genetic algorithms. Hydrol. Process. Int. J. 2006, 20, 2057–2075. [Google Scholar] [CrossRef]
- Ming, B.; Chang, J.-X.; Huang, Q.; Wang, Y.-M.; Huang, S.-Z. Optimal Operation of Multi-Reservoir System Based-On Cuckoo Search Algorithm. Water Resour. Manag. 2015, 29, 5671–5687. [Google Scholar] [CrossRef]
- Ostadrahimi, L.; Mariño, M.A.; Afshar, A. Multi-reservoir operation rules: Multi-swarm PSO-based optimization approach. Water Resour. Manag. 2012, 26, 407–427. [Google Scholar] [CrossRef]
- Ming, B.; Liu, P.; Cheng, L.; Zhou, Y.; Wang, X. Optimal daily generation scheduling of large hydro–photovoltaic hybrid power plants. Energy Convers. Manag. 2018, 171, 528–540. [Google Scholar] [CrossRef]
- Reddy, J.M.; Kumar, N.D. Multi-objective differential evolution with application to reservoir system optimization. J. Comput. Civ. Eng. 2007, 21, 136–146. [Google Scholar] [CrossRef]
- Reddy, M.J.; Kumar, D.N. Performance evaluation of elitist-mutated multi-objective particle swarm optimization for integrated water resources management. J. Hydroinform. 2009, 11, 79–88. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Chang, J.; Meng, X.; Wang, Y. Research on multi-objective operation based on improved NSGA-II for lower Yellow River. J. Hydraul. Eng. 2017, 48, 135–145. [Google Scholar]
- Yang, W. Study on Multi-Objective Conversion Law of Joint Operation of Heihe Cascade Reservoir Group; Xi’an University of Technology: Xi’an, China, 2018. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas; Springer: New York, NY, USA, 2006. [Google Scholar]
- Li, J.; Zhang, Q.; Chen, Y.D.; Singh, V.P. Future joint probability behaviors of precipitation extremes across China: Spatiotemporal patterns and implications for flood and drought hazards. Planet. Chang. 2015, 124, 107–122. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Zhang, Q.; Xiao, M.; Singh, V.P.; Zhang, S. Probabilistic forecasting of seasonal droughts in the Pearl River basin, China. Stoch. Environ. Res. Risk Assess. 2016, 30, 2031–2040. [Google Scholar] [CrossRef]
- Goswami, U.P.; Bhargav, K.; Hazra, B.; Goyal, M.K. Spatiotemporal and joint probability behavior of temperature extremes over the Himalayan region under changing climate. Theor. Appl. Climatol. 2018, 134, 477–498. [Google Scholar] [CrossRef]
- Sraj, M.; Bezak, N.; Brilly, M. Bivariate flood frequency analysis using the copula function: A case study of the Litija station on the Sava River. Hydrol. Process. 2015, 29, 225–238. [Google Scholar] [CrossRef]
- Huang, S.; Chang, J.; Huang, Q.; Chen, Y. Spatio-temporal changes and frequency analysis of drought in the Wei River Basin, China. Water Resour. Manag. 2014, 28, 3095–3110. [Google Scholar] [CrossRef]
- Fang, W.; Huang, S.; Huang, G.; Huang, Q.; Wang, H.; Wang, L.; Zhang, Y.; Li, P.; Ma, L. Copulas-based risk analysis for inter-seasonal combinations of wet and dry conditions under a changing climate. Int. J. Climatol. 2019, 39, 2005–2021. [Google Scholar] [CrossRef]
- Chen, F.; Huang, G.; Fan, Y.; Chen, J. A copula-based fuzzy chance-constrained programming model and its application to electric power generation systems planning. Appl. Energy 2017, 187, 291–309. [Google Scholar] [CrossRef]
- Yu, L.; Li, Y.; Huang, G.; Fan, Y.; Nie, S. A copula-based flexible-stochastic programming method for planning regional energy system under multiple uncertainties: A case study of the urban agglomeration of Beijing and Tianjin. Appl. Energy 2018, 210, 60–74. [Google Scholar] [CrossRef]
- Kong, X.M.; Huang, G.H.; Li, Y.P.; Fan, Y.R.; Zeng, X.T.; Zhu, Y. Inexact Copula-Based Stochastic Programming Method for Water Resources Management under Multiple Uncertainties. J. Water Resour. Plan. Manag. 2018, 144, 04018069. [Google Scholar] [CrossRef]
- Fan, Y.R.; Huang, G.H.; Baetz, B.W.; Li, Y.P. Development of a copula-based particle filter (CopPF) approach for hydrologic data assimilation under consideration of parameter interdependence. Water Resour. 2017, 53, 4850–4875. [Google Scholar] [CrossRef]
- Guo, S.; Yan, B.; Xiao, Y.; Fang, B.; Zhang, N. Application and research progress of Copula function in multivariate hydrological analysis and computation. J. China Hydrol. 2008, 28, 1–7. [Google Scholar]
- Zhao, J.; Xu, Z.-X.; Zuo, D.-P.; Wang, X.-M. Temporal variations of reference evapotranspiration and its sensitivity to meteorological factors in Heihe River Basin, China. Water Sci. Eng. 2015, 8, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Min, L.; Yu, J.; Liu, C.; Zhu, J.; Wang, P. The spatial variability of streambed vertical hydraulic conductivity in an intermittent river, northwestern China. Environ. Earth Sci. 2013, 69, 873–883. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, Q.; Chen, L.; Yu, T. Significance and Effect of Ecological Rehabilitation Project in Inland River Basins in Northwest China. Environ. Manag. 2013, 52, 209–220. [Google Scholar] [Green Version]
- Goldberg, D.E.; Deb, K. A Comparative Analysis of Selection Schemes Used in Genetic Algorithms. Found. Genet. Algorithms 1991, 1, 69–93. [Google Scholar] [Green Version]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Paris, France, 18–20 September 2000; Springer: Berlin/Heidelberg, Germany, 2000; pp. 849–858. [Google Scholar]
- Sklar, M. Fonctions de repartition an dimensions et leurs marges. Publ. Inst. Statist. Univ. Paris 1959, 8, 229–231. [Google Scholar]
- Shiau, J.-T. Fitting Drought Duration and Severity with Two-Dimensional Copulas. Water Resour. Manag. 2006, 20, 795–815. [Google Scholar] [CrossRef]
- Guo, Y.; Huang, S.; Huang, Q.; Wang, H.; Fang, W.; Yang, Y.; Wang, L. Assessing socioeconomic drought based on an improved Multivariate Standardized Reliability and Resilience Index. J. Hydrol. 2019, 568, 904–918. [Google Scholar] [CrossRef]
- Yue, S.; Ouarda, T.; Bobée, B.; Legendre, P.; Bruneau, P. The Gumbel mixed model for flood frequency analysis. J. Hydrol. 1999, 226, 88–100. [Google Scholar] [CrossRef]
- Zhao, M.; Huang, S.; Huang, Q.; Wang, H.; Leng, G.; Xie, Y. Assessing socio-economic drought evolution characteristics and their possible meteorological driving force. Geomat. Hazards Risk 2019, 10, 1084–1101. [Google Scholar] [CrossRef]
- Guindon, S.; Gascuel, O. A Simple, Fast, and Accurate Algorithm to Estimate Large Phylogenies by Maximum Likelihood. Syst. Biol. 2003, 52, 696–704. [Google Scholar] [CrossRef] [Green Version]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Yang, T.; Tao, Y.; Li, J.; Zhu, Q.; Su, L.; He, X.; Zhang, X. Multi-criterion model ensemble of CMIP5 surface air temperature over China. Theor. Appl. Clim. 2017, 132, 1057–1072. [Google Scholar] [CrossRef]












| No. | Annual Water Shortage in Irrigation (104 m3) | Annual Water Shortage in Ecological (104 m3) | Annual Generation Capacity (108 kW·h) |
|---|---|---|---|
| 1 | 925 | 9058 | 25.95 |
| 2 | 926 | 9010 | 25.94 |
| 3 | 935 | 9000 | 25.96 |
| … | … | … | … |
| 1998 | 6580 | 4396 | 26.34 |
| 1999 | 6584 | 4400 | 26.34 |
| 2000 | 6595 | 4424 | 26.35 |
| Objective Combination | Clayton Copula | Frank Copula | Gumbel Copula | Gaussian Copula | Student Copula |
|---|---|---|---|---|---|
| Obj-1&2 | −8635.43 | −16,051.64 | −8635.43 | −16,435.24 | −16,437.86 |
| Obj-1&3 | −10,140.03 | −10,629.38 | −10,140.03 | −10,671.15 | −10,669.85 |
| Obj-2&3 | −10,075.94 | −11,292.73 | −10,075.93 | −11,282.21 | −11,281.74 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, M.; Huang, S.; Huang, Q.; Wang, H.; Leng, G.; Liu, S.; Wang, L. Copula-Based Research on the Multi-Objective Competition Mechanism in Cascade Reservoirs Optimal Operation. Water 2019, 11, 995. https://doi.org/10.3390/w11050995
Zhao M, Huang S, Huang Q, Wang H, Leng G, Liu S, Wang L. Copula-Based Research on the Multi-Objective Competition Mechanism in Cascade Reservoirs Optimal Operation. Water. 2019; 11(5):995. https://doi.org/10.3390/w11050995
Chicago/Turabian StyleZhao, Menglong, Shengzhi Huang, Qiang Huang, Hao Wang, Guoyong Leng, Siyuan Liu, and Lu Wang. 2019. "Copula-Based Research on the Multi-Objective Competition Mechanism in Cascade Reservoirs Optimal Operation" Water 11, no. 5: 995. https://doi.org/10.3390/w11050995
APA StyleZhao, M., Huang, S., Huang, Q., Wang, H., Leng, G., Liu, S., & Wang, L. (2019). Copula-Based Research on the Multi-Objective Competition Mechanism in Cascade Reservoirs Optimal Operation. Water, 11(5), 995. https://doi.org/10.3390/w11050995