Next Article in Journal
Aeroelastic Performance Analysis of Wind Turbine in the Wake with a New Elastic Actuator Line Model
Next Article in Special Issue
Effects of Land Use Changes on Streamflow and Sediment Yield in Atibaia River Basin—SP, Brazil
Previous Article in Journal
Spatial and Temporal Characterization of Escherichia coli, Suspended Particulate Matter and Land Use Practice Relationships in a Mixed-Land Use Contemporary Watershed
Previous Article in Special Issue
Impacts of Climate Change and Land Use/Cover Change on Streamflow in Beichuan River Basin in Qinghai Province, China
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 12
Issue 5
10.3390/w12051232
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Laser Diffraction as An Innovative Alternative to Standard Pipette Method for Determination of Soil Texture Classes in Central Europe

by
Dušan Igaz
1,*,
Elena Aydin
1,*,
Miroslava Šinkovičová
1,
Vladimír Šimanský
2,
Andrej Tall
3 and
Ján Horák
1
1
Department of Biometeorology and Hydrology, Slovak University of Agriculture, 94976 Nitra, Slovakia
2
Department of Soil Science, Slovak University of Agriculture, 94901 Nitra, Slovakia
3
Institute of Hydrology Slovak Academy of Sciences, 84104 Bratislava, Slovakia
*
Authors to whom correspondence should be addressed.
Water 2020, 12(5), 1232; https://doi.org/10.3390/w12051232
Submission received: 24 March 2020 / Revised: 21 April 2020 / Accepted: 22 April 2020 / Published: 26 April 2020
(This article belongs to the Special Issue Hydrological Impacts of Climate Change and Land Use)
Browse Figures
Versions Notes

Abstract

:
The paper presents the comparison of soil particle size distribution determined by standard pipette method and laser diffraction. Based on the obtained results (542 soil samples from 271 sites located in the Nitra, Váh and Hron River basins), regression models were calculated to convert the results of the particle size distribution by laser diffraction to pipette method. Considering one of the most common soil texture classification systems used in Slovakia (according to Novák), the emphasis was placed on the determination accuracy of particle size fraction <0.01 mm. Analysette22 MicroTec plus and Mastersizer2000 devices were used for laser diffraction. Polynomial regression model resulted in the best approximation of measurements by laser diffraction to values obtained by pipette method. In the case of particle size fraction <0.01 mm, the differences between the measured values by pipette method and both laser analyzers ranged in average from 3% up to 9% and from 2% up to 11% in the case of Analysette22 and Mastersizer2000, respectively. After correction, the differences decreased to average 3.28% (Analysette22) and 2.24% (Mastersizer2000) in comparison with pipette method. After recalculation of the data, laser diffraction can be used alongside the sedimentation methods.

Graphical Abstract

1. Introduction

The mineral constituent of the soil’s solid phase is composed of differently sized fundamental particles. These mineral soil particles of defined size are divided into groups, which are referred to as particle size fractions, and which, in addition to their similar dimensions, have more or less the same basic physical and physical-chemical properties. The amount and speed of processes taking place in the soil are influenced by the proportion of individual particle size fractions. Particle size distribution is regarded as one of the basic physical characteristics, and therefore soil studies should begin by determining it [1,2,3]. The knowledge about the particle size distribution of soils is of fundamental importance in terms of soil genesis, agronomy, and soil hydrology [4,5,6,7]. From the genetic point of view, it is possible to evaluate the soil-forming processes and the soil profile heterogeneity. From the agronomic point of view, the importance of soil texture is associated with the implementation of various amelioration measures, such as drainage, irrigation, compaction of coarse soils, aeration, and increasing of permeability of fine soils. From the hydrological point of view, the soil particle size distribution is essential for water movement in the soil profile as it influences infiltration rate, water holding capacity, water content constants, and hydraulic conductivity, and the overall hydrological balance of the area [8,9,10]. The results of the particle size analyses are of key importance for plant fertilization and liming, and also for the actual cultivation of the soil, e.g., determination of difficultness and effortfulness of agronomical interventions.
The size of soil particles plays the most important role in their distribution in the soil. The representation of individual particle size fractions can be obtained in several ways. The most common method of particle size determination is sieving of soil using the set of sieves [11], finer fractions are obtained using sedimentation methods. Sedimentation methods are based on the Stokes’ Law—formulated in 1851: “The resistance of liquid to the fall of solid spherical particles varies according to the particle radiuses not their surface” [12,13]. Sedimentation methods are based on the principle that the particle sedimentation drop velocity in water suspension depends on the particle size and the liquid properties. Pipette method (PM) belongs to the group of methods using nonrepetitive sedimentation of soil particles, which is considered to be one of the least demanding, but the most accurate (accuracy of 2.3%), methods in soil science ever. However, a rather lengthy duration of the particle size analysis is its disadvantage [5,14]. In Slovakia and abroad, the pipette method is still the most commonly used method in soil science practice [5,14,15]. Additionally, with the development of sophisticated instrumentation, direct (such as microscopy) and indirect optical methods (such as laser diffraction) have been used, especially in recent decades. Rather recently, Allen [16] has started to use the laser diffraction method (LD) for particle size distribution determination in soil science, and its applicability in soil science and related fields has begun to increase in the recent years [1,3,17,18]. Laser diffraction analysis determines the particle size indirectly based on the angle of the reflected laser beam from the particle with inverse proportionality [19]. It is a relatively simple and fast method [20,21], but there is no uniform standard methodology for soil sample preparation and the analysis itself. Although ISO 13320:2009 [22] recommends preparing a sample of the analyzed material by adding a dispersing agent dropwise, the consistency of the resulting paste is strongly left to subjective opinion and experience of the operating staff. Moreover, the results on particle size distribution for the same sample determined by laser diffraction and pipette method are not equal due to the different physical principles on which the methods are based. This incompatibility in the results can limit the applicability of laser diffraction soil analysis in engineering and computer modelling [19,22,23,24,25,26].
In the past decade, several authors have been involved in the determination of particle size distribution by LD, trying to unify the obtained results with the standard PM in soil science [1,3,27,28,29,30,31,32]. The differences in their results and methodologies are based mainly on the different methods of soil sample preparation prior to analysis (such as different amounts of soil and dispersion agents used), different LD devices and their settings. Since the conversion of results from LD to PM is influenced by a number of factors and the results cannot be compared without further processing [27,33,34,35], there is an effort to create regression models that allow recalculation of the LD results to values comparable to sedimentation methods. Statistical analysis of the results obtained by LD and PM has been performed abroad by several authors [23,28,29,36,37,38]. However, statistical relationships derived by one author are rarely applicable to other authors due to differences in LD instrumentation, measurement range, use of Mie or Fraunhofer calculation theory, and, last but not least, interpretation of the obtained results in different particle size and soil texture classification systems.
Soil texture classes are determined based on the percentage representation of individual particle size fractions, using different classification systems worldwide. One of the most commonly used is the soil texture triangle classification according to United States Department of Agriculture (USDA) [39] that uses the representation of the three basic particle size fractions of sand (0.005–2 mm), silt (0.002–0.005 mm), and clay (particles below 0.002 mm). According to Bedrna and Ofránus [40], the usage of USDA triangle classification in Slovakia is only recent and primarily used for specification of particle size distribution of mineral soils in the morphogenetic soil classification [41]. However, there are also other particle size fraction classification systems used alongside USDA (Table S1), and while some are at least partially compatible with the USDA system [42,43], the rest is hardly comparable due to focus on different particle size fractions. Many countries in Central and Eastern Europe (e.g., Czech Republic, Slovakia, Bulgaria) as well as countries of former USSR and China adopted the classification of particle size fractions according to Kachinski [44,45]. The simplified classification according to Kachinski was also adopted for the purposes of past soil surveys done on the national level in Slovakia. The soil texture classification system of Slovakia (Novak’s classification) originates in the Kachinski system, and soil texture is evaluated according to the percentage particles below 0.01 mm [5] (Table 1). General soil texture classes (light, medium heavy, and heavy soils) refer to easiness in cultivation and the impact of cultivation tools on the soil [44]. A complex soil survey (CSS) (1960–1970) collected information on soil texture and other basic soil properties in the agricultural soils in the former Czechoslovakia. The subsequent soil quality evaluation (soil bonitation) (1972–1978) [46] used the collected information, along with other purposes, to elaborate maps of evaluated (bonitated) soil-ecological units (ESEU). Up till now, the maps of ESEU have been widely used for land consolidation and landscape conservation projects [47,48]. This system also provides data for legislation, determination of land tax, for exchange of land, and for decision-making by authorities in cases of interest to use agricultural land for nonagricultural purposes [49].
As it was mentioned before, the USDA classification was already introduced in Slovakia, however, its usage is still very limited. One of the main reasons is that the soil-related studies done in Slovakia in the past mostly refer to Novak’s classification of soil texture and provide relevant data such as bulk density, hydrolimits (water content constants), permeability of soil, level of maintenance, and other for soil texture classes according to this classification. Moreover, this assessment is still commonly used in the agronomic practice.
It is obvious that the use of different methods for the determination of particle size distribution has its limitations, starting from different sample preparation prior to analysis and ending with different determination principles, which makes the interpretation and evaluation of results considerably more difficult. If the results are to be obtained as quickly as possible with satisfactory quality to conventional agronomy, hydrology, and soil science, it is necessary to focus on comparing results obtained by PM and LD. Because of differences in size fractions between the USDA soil texture triangle and Novak’s soil classification system, the findings already published abroad are not applicable to the conditions of Slovakia.
Therefore, the aim of this work was (i) to compare the results of the particle size analysis obtained by the standard pipette method and the laser diffraction method, (ii) based on the obtained results, to create a regression model that would convert laser diffraction results into a pipette method with at least 95% accuracy. We aimed especially at fraction <0.01 mm, because it is the fundamental fraction for soil texture determination in countries implementing the classification system of particle size fractions according to Kachinski and Novák’s classification of soil texture classes.

2. Materials and Methods

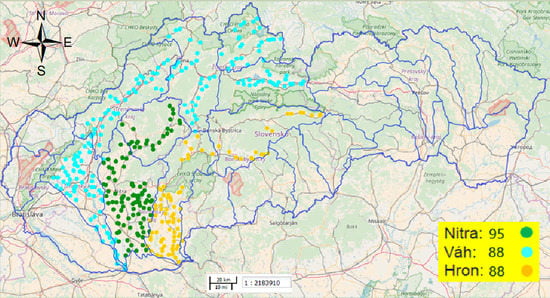
2.1. Study Area

The area of interest (total area 24,234 km2) consisted of three neighboring basins of Váh River (total area = 14,268 km2), Nitra River (total area = 4501 km2), and Hron River (total area = 5465 km2) located in the western and central part of Slovakia (Figure 1). According to the orographic division, the territory is located in the orographic sub-system of the Carpathian Mountains and the Pannonian Basin [51].
The terrain of Váh River basin is very complex and includes all types of relief, from the plains and hills up to the mountains of high altitude. The majority of the basin’s altitude ranges from 400 m up to 800 m. In terms of climatic conditions, the basin belongs to a warm, moderate, and cold climatic area. Long-term average annual air temperature in warm lowland areas ranges from 11 up to 12 °C, in moderate area with rising altitude it decreases to 9–10 °C, and it reaches 4–7 °C in cold climatic area. The average annual rainfall in the warm area is around 500–550 mm, in the moderate area 800 mm, in the highest positions from 1200–1600 mm, and in the ridges of the Tatras up to 2000 mm. From the pedological point of view, there are Chernozems, Luvisols in the lower part of the basin and Fluvisols along the river body. Skeletic, Lithic and Rendzic Leptosols, Cambisols, Stagnosols, and Podzols are located in the mountain ranges. Agricultural land accounts for 38.3% of the river basin area.
The Nitra River basin is located between the Váh River basin from the north and the Hron River basin from the west. The average altitude of the basin is 326 m. In terms of climatic conditions, the basin belongs to three climatic areas. The warm climatic area occupies two-thirds of the territory and is located in the Danube Lowland, and in hollows and river sub-basins. The central part of the basin is located in the temperate climate area. The cold climate area has very little representation. Long-term average annual precipitation of the whole basin area is 733 mm. Areas with a higher altitude have the average annual rainfall in the range of 1200–1500 mm. Fluvisols, Cambisols, and Chernozems are the most represented soil types in the river basin, followed by Luvisols and Podzols. Agricultural land accounts for 69.1% of the river basin area.
The Hron River basin is very rugged, with the largest part of the basin located in highlands with an altitude of 300–800 m. All types of relief—from plains, uplands, to highlands—can be found in the river basin. The basin is located in three climatic areas. Warm climate area is represented from the altitudes of 200–250 m where the average annual air temperature 9.5 °C with an annual rainfall in the range of 550–700 mm. The moderate climate area is represented from the altitudes of 750–800 m where the average annual air temperature reaches 6–8 °C and average annual rainfall is 700–900 mm. The higher altitudes belong to a cold climate area with an average annual air temperature of 4–5 °C and rainfall of more than 900 mm. The soils in the basin are mainly Chernozems and Luvisols; Rendzic Leptosols, Calcaric Cambisols, Fluvisols, Podzols, and Stagnosols are represented less often. Agricultural land accounts for 47.2% of the river basin area.
Soil sampling in the above-mentioned basins was conducted as a part of a bigger study, in which the disturbed and undisturbed soil samples were taken from specific locations and were used for soil analysis of the basic physical and hydrophysical properties. The results were reported in the scientific monograph by Skalová et al. [51]. The location of sampling areas was determined according to maps of ESEU to obtain a network of sampling locations representing approximately the area of 6 × 6 km2. The sampling point was chosen at least 300 m aside from the expected border of specific ESEU (there is a potential of its shifting within a year due to tillage etc.). Information of soil texture classes from maps of ESEU was used to ensure that the general percentage distribution of soil texture classes on the agricultural land in the basins would correspond to the representation of soil texture classes at the sampling sites. For the purposes of soil texture analysis by pipette method, disturbed soil samples were taken only from agricultural land from two depths, 15–20 cm and 40–45 cm (Figure S1). In total, 542 samples were taken from 271 sampling sites (Figure 1), consisting of 190, 176, and 176 samples from the Nitra, Váh, and Hron River basins, respectively (Figures S2–S4). Subsequently, for the purposes of our study, the same soil samples were analyzed by the particle size analyzers using laser diffraction method.

2.2. Soil Analysis by Pipette Method

Carbonates (CaCO3) were removed from a representative soil sample prepared from air-dried and sieved fine soil (particles <2 mm) using 2 mol·dm−3 HCl. Organic substances were removed by 6% hydrogen peroxide (H2O2). After repeated washing, soil samples were dispersed with a solution of 0.06 mol·dm−3 sodium hexaphosphate (NaPO3)6 and 0.075 mol·dm−3 sodium carbonate (Na2CO3). Using the pipette method, the proportion of five particle size fractions used in the complex soil survey (CSS) was determined in the soil sample as described in Hrivňáková et al. [14]. The obtained particle size fractions were coarse sand (0.25–2 mm), medium and fine sand (0.05–0.25 mm), coarse silt (0.01–0.05 mm), medium and fine silt (0.001–0.01 mm), and clay fraction (<0.001 mm). Content of particles with diameter <0.01 mm was calculated as the sum of the medium silt, fine silt, and clay fraction.

2.3. Soil Analysis by Laser Diffraction Method

Representative soil samples (10 g) were prepared by quartering air-dried sieved fine soil (particles <2 mm). Next, soil samples were mixed with 10 mL of 0.05 M sodium polyphosphate (Graham’s salt (NaPO3)n). After dispersing for 24 h, prior to laser diffraction analysis, the samples were treated with ultrasound for the duration of 5 min to completely break the soil aggregates in the suspension [5]. Measurements by laser diffraction method (LD) were conducted using two laser analyzers: Analysette22 MicroTec plus and Mastersizer2000.
The laser analyzer Analysette22 MicroTec plus (Fritsch, Germany) (LD 22) (Figure S5) was operated by the MaScontrol software, which provided control and evaluation functions and performed extensive calculations of the measured data stored in the database. The measurement was conducted in the full measuring range of the device (0.08–2000 μm), at the ultrasound intensity of 2, and the sample was mixed by built-in stirrer for 3 min prior to measurement [5]. Considering the heterogeneity of the soil of different origin from three studied river basins, Fraunhofer calculation model was chosen for the particle size distribution calculation. This model does not require the information on the light refraction index of dispersion fluid, neither the refraction of light by the soil particles nor the absorption index [34]. The Mastersizer2000 laser analyzer (Malvern, UK) (LD_2000) (Figure S6) was operated by the Malvern SOP software, and some tasks were also performed manually. The measurements were conducted in the full measuring range of the device (0.02–2000 μm). The instrument settings were the same as in the case of the former analyzer.
Each sample was measured at least three times until the differences in the percentage of clayey fraction for three individual measurements were less than 2%. Results on soil particle size distribution were reported in the cumulative particle size fractions according to CSS classification: <0.001 mm; <0.01 mm; <0.05 mm; <0.25 mm, and <2 mm.

2.4. Statistical Analyses

The results were evaluated using Statgraphics Centurion XV.I statistical software (Statpoint Technologies, Inc., Warrenton, VA, USA). To determine the statistical dependence between the PM and LD, 271 samples were randomly selected from a set of total 542 soil samples. Results obtained for the same soil samples by PM and LD were input data for regression analyses using linear, exponential, polynomial, power, and logarithmic models with focus on Pearson’s correlation coefficient between dependent variable Y (PM) and independent variable X (LD). We worked with 95% reliability, where the error of estimation was 5%.
The remaining 271 soil samples were used for verification of the observed dependence expressed by regression equations. The measured values by LD were substituted for term X in the regression equations for three models with the highest reliability (linear model (LM), exponential model (EM), and polynomial model (PM)) to calculate the estimated value on particle size distribution by PM (PMestLM, PMestEM, and PMestPM, respectively). Measured values by pipette method (PMme) were then deducted from the estimated values. The mean values of these differences were used for the statistical comparison of the original (PMme) and calculated (PMestLM, PMestEM and PMestPM) results.

3. Results

3.1. Distribution of the Soil Texture Classes in the Study Area

According to the results on particle size distribution by PM for soil samples from all basins and both depths, medium heavy soils (according to Novak’s classification of soil texture classes) was the most represented soil texture class (73%) (Figure S7; Table S2). Heavy soils were represented by 17% and light soils by 10% in whole sample dataset. The proportion of soil texture classes in the individual basins was approximately the same, with two exceptions. In the Nitra River basin area, medium heavy loamy soils were more prominent (up to 120 samples), representing 63% of the samples from this river basin. In the Váh River and Hron River basins, loamy soils were less prevalent (43% and 23%, respectively). On the other hand, light loam-sandy soils were more represented in the Hron River basin (18%) when compared with the Váh River and Nitra River basins (7% and 4%, respectively). According to mean percentage distribution of particle size fractions in the individual basins determined by PM, the representation of particle size fractions was very similar in every basin (Table S3).

3.2. Developing the Relationships between the Results of PM and LD

As mentioned in the methodology part, 50% of the soil samples were used for determination of the regression models between the representation of cumulative particle size fractions determined by two types of laser analyzers and PM (Figure 2). When comparing the cumulative values on particle size fraction distribution determined by LD and PM in the ratio 1:1, it was found that LD generally underestimated representation of fraction <0.001 mm and overestimated representation of fractions <0.01 mm, <0.05 mm, and <0.25 mm.
Figure 3, Figure 4 and Figure 5 present the relationships for three regression models with the highest values of the determination coefficient R2 between the particle size distribution as observed by LD and PM analyses. The regression function for the polynomial trend has the following general form:
Y = b2 × X2 + b1 × X1 + b0,
where
  • Y—dependent variable.
  • b2—coefficient 2.
  • X2—independent variable 2.
  • b1—coefficient 1.
  • X1—independent variable 1.
  • b0—constant.
The polynomial regression model appeared to be the best fitting, when the coefficient of determination at the selected level of significance alpha = 0.05 was 0.7664 for Analysette22 MicroTec plus and 0.8467 for Mastersizer2000 (Figure 5). These values indicate that the selected regression model explained the variability to approximately 76.64% and 84.67% for Analysette22 MicroTec plus and Mastersizer2000, respectively, while the rest was related to unexplained variability, the effect of random factors and other unspecified effects.
The selected models were statistically verified with 95% reliability for both used laser analyzers (Table 2). In the one-way ANOVA section, we tested the null hypothesis, whether the model was appropriate, and whether the variables of the model were correlated with the dependent variable. The F test was used to evaluate this claim, where the overall Significance F values were <0.05, which meant that the models were chosen correctly. In case of Analysette22 MicroTec plus, the polynomial regression model was overall statistically significant (Significance F = 0 <0.05), including the constant (p-value for intercept = 0 <0.05) and regression coefficients (p-values for X variables were 0.0342 for b1 and 0 for b2). The polynomial model for Mastersizer2000 was also statistically significant overall (Significance F = 0 <0.05), including the constant (p-value for intercept = 0 <0.05) and regression coefficients (p-values for X variables were 0.0218 for b1 and 0 for b2). Similarly, the suitability of the linear and exponential models was verified (Table 2).

3.3. Verification of the Relationship between PM and LD

Table 3 shows the verification of the results according to comparison of the calculated values using LD and different regression models—estimates (PMestLM, PMestEM, and PMestPM) with originally measured PM values (PMme) for the second group of soil data (not used for determination of the regression models). When validating the results, the differences (absolute values) between the estimated and measured values (Analysette22 MicroTec plus vs. PM) ranged from 0.75% up to 5.18%, from 2.31% up to 14.99%, and from 0.98% up to 3.8% for cumulative particle size fractions <0.001 mm, <0.01 mm, and <0.25 mm, respectively. Estimates of the representation of particle size fraction <2 mm according to LD regression models were lower by 11.91% up to 15.11%. When considering the results obtained by LD, Mastersizer2000 vs. PM, the differences (absolute values) between the estimated and measured PM values were generally smaller than in the case of Analysette22 MicroTec plus. The mean absolute differences for cumulative particle size fractions <0.001 mm, <0.01 mm, <0.05, and <0.25 mm ranged from 1.92% to 4.28%, from 0.79% to 11.43%, from 0.95% to 1.36%, and from 2.25% to 8.29%, respectively. However, high underestimation of the particle size distribution was observed for LD estimate of the fraction <2 mm, with values ranging from 6.16% up to 10.89% (Table 3).
In general, estimated values obtained by LD resulted in underestimation of the particle size distribution of the fraction <0.001 mm and overestimation for the fractions <0.01 mm, <0.05 mm, and <0.25 mm when compared with PMme. Taking into account soil samples from all basins analyzed by both analyzers, the differences between the estimated values for PMestPM (polynomial model) and measured values (PMme) were relatively small (up to 6%) for fractions <0.001 mm, <0.01 mm, <0.05 mm, and <0.25 mm. Determination accuracy of particle size fractions <0.25 mm and <2 mm was lower (up to 12%).

3.4. Aproximation of LD Results to PM

Using Analysette22 MicroTec plus laser analyzer, the approximate value of the required particle size fraction (<0.01 mm) for the pipette method can be calculated according to the following equation:
Y = 0.00775 × X2 − 0.12095 × X + 22.7716,
where Y—estimated representation of specific particle size fraction for pipette method (%).
X—measured representation of specific particle size fraction by Analysette22 MicroTec plus (%).
Using Mastersizer2000 laser analyzer, the approximate value of the required particle size fraction can be calculated according to the following equation:
Y = 0.0065 × X2 − 0.095 × X + 18.889,
where Y—estimated representation of specific particle size fraction for pipette method (%).
X—measured representation of specific particle size fraction by Mastersizer2000 (%).
The above-mentioned equations are recommended for estimation of the content of particle size fraction <0.01 mm. In the case of this particle size fraction, the average differences between the estimated values (PMestPM) using LD and the real measured values (PMme) were 3.28% and 2.24% in the case of laser analyzers Analysette 22 MicroTech plus and Mastersizer2000, respectively (Table 3). This difference can be considered as acceptable for repeated measurements conducted for heterogeneous matter such as soil. Moreover, the obtained differences are comparable with the pipette method.
In addition, the derived equations can be also used for estimation of cumulative particle size fractions <0.001 mm and <0.25 mm in the case of Mastersizer2000 and <0.25 mm in the case of Analysette22. On the other hand, the same relationships are less suitable for estimation of particle size fractions (and fractions in their proximity) <0.05 mm and above 0.25 mm, and other approaches must be sought for reliable conversion of the representation from LD to PM.

4. Discussion

4.1. Comparison of Results by PM and LD Analysis

Many teams have been working on the development of unified methodology and regression models that allow conversion of results by LD to the values comparable to sedimentation methods [2,27,28,29]. So far, the comparison of the standard methods with LD has been done by means of regression analysis for the whole dataset [53] or specific particle size fractions [30,38,54,55]. Other approaches involved methods such as network analysis [55], regression tree, and Random Forest [54].
Although relationships were found between the LD-derived and the PM-derived data for the soil samples in our study, there were differences observed for both LD devices. This type of dissimilarity implies that attempts to convert LD-derived volume percentage of a given size fraction to mass percentage by PM (or vice versa) will not be accurate and thus be of limited value [38]. Since the purpose of this study was to find alternative methodology of particle size distribution determination using LD (including the specific sample preparation method) to be used also in praxis for analysis of samples of unknown soil texture, we used whole dataset. Dividing the soil sample dataset according to distribution of soil texture classes in the study area would lead to less samples for studying the relationship for a specific soil texture class. Since medium heavy soils are apparently prevailing in our dataset, we conclude that the best fit will be therefore obtained for medium heavy soils using our methodology. However, considering the fact that we kept the percentage distribution of soil textural classes occurring in the basins similar to the representation of soil samples in the dataset, we assume that the methodology can be used for soil texture analysis in the mentioned basins as well as in areas with similar conditions. In total, 542 soil samples were used in this study, of which 271 were used for determining the relationship between PM and LD measurements. Some other published studies are based on a dataset of 10–37 samples [30,53,55,56]. Miller and Schaetzl [57] published a study with 1485 samples, however those were analyzed only by LD as the study was aimed to precision of soil particle size analysis using LD.
Konert and Vandenberghe [58] published a study comparing the PM with the LD and found that while there was only a slight difference between the representation of sand fraction determined by both methods, the representation of clay fraction (<0.002 mm) was significantly underestimated by LD. This observation corresponds with our findings, although in our study, particle size fraction <0.001 mm was determined (Figure 2).
When comparing LD with PM, Kun et al. [28] found the greatest difference for clay fraction content (<0.002 mm), which also increased the error and likelihood of underestimation in LD [58,59]. In case of high clay content in the soil sample, LD seemed to underestimate the clay fraction content in favor of the silt fraction (0.002–0.02 mm). At the same time, PM seemed to overestimate the clay fraction due to the assumed spherical shape of the clay particles [28]. Konert and Vandenberghe [58] tried to correct the representation of overestimated silt fraction. Kun et al. [28] suggested that PM systematically overestimated the sand fraction (0.02–2000 mm) when compared with LD. The same authors also assumed, that LD underestimated the sand fraction in favor of the silt fraction due to the rough surface of the sand particles. Due to usage of different particle size fraction classification (USDA) in foreign studies, comparison of our observations with the published findings can only be approximate. However, the findings by Kun et al. [28] can also be observed as a trend in our study (applies to both LD devices). Similar to underestimation of the sand fraction (0.02–2000 mm) in their study, the content of particles with diameter above 0.25 mm was also underestimated in our study. This deviation is proportional to the particle diameter in the range indicated above.
Deviations from the spherical shape of mineral particles and deviations in their particle density could be the main reason for these differences [30]. According to Eshel et al. [38], the mere assumption of a single value (of quartz) for particle density in soils, as is presumed for the purpose of particle size determinations by the pipette method, is an obvious source of error. Particle density of soil components may vary between soils and even among different size fractions in specific soil.

4.2. Comparison of Results by Two LD Devices

Differences in results were also observed for the two particle size analyzers used in this study (Figure 3, Figure 4 and Figure 5), although the measurement was based on the same principle. The outlying results in our study are related to the representation of cumulative particle size fraction ˂0.25 mm mainly in the Nitra River basin (one sample is located in the Hron River basin). Laser diffraction analysis by wet method can be problematic for soils with high content of heavier particles, such as sandy, loam-sandy and sandy-loam soils, similar to our case. Excluding the potential of human error in the measurements, the differences in construction and operation still could play a role, although the same methodology was used. In case of Analysette22 MicroTec plus, the dispersion unit is filled and emptied under the command from the software, and the tank for dispersion liquid and sample is built into the device. Contrary to this, in case of Hydro MU wet dispersion unit of Mastersizer2000, the transparent glass beaker with volume 1000 mL is filled manually. If the sedimentation of the sample occurs in spite of mixing, it can be observed more easily. We also concluded that in case of Analysette22 MicroTec plus, the pump speed should be higher, because the sample circulates in the system (dispersion unit-measuring cell-dispersion unit) with higher vertical difference. However, in this study, we tried to use the same settings since we wanted to test the applicability of our methodology (of sample preparation and measurement by laser diffraction) also on a device by another manufacturer. Nevertheless, it is not surprising to obtain different results [38], since differences in measurements were observed even for the laser analyzers made by the same producer (e.g., Sochan et al. [60]). Finally, Mastersizer2000 has a wider measuring range (0.02–2000 μm) in comparison with Analysette22 MicroTec plus (0.08–2000 μm) and it results in different detection limits [38].

4.3. Comparison of PM and LD Method

Eshel et al. [38] suggest that the choice between the particle size analysis methods should be balanced depending on their pros and cons. The advantage of LD in comparison with PM in general is the considerably shorter time of analysis, need of a small sample for analysis, and that distribution of group of size fractions is evaluated at the same time. Thus, elaborating the particle size distribution curve is not limited. In contrary, according to Eshel et al. [38] the disadvantage of LD is the high cost of the instrumentation and the lack of a database that would correlate LD-derived distribution of particle sizes with soil properties, similarly to the extensive database existing for PM. Moreover, every laboratory aiming to use LD for particle size distribution of soil samples or samples of similar heterogenic composition must firstly solve the issue of correlating the LD measurements by specific instrument with standard methods. Otherwise, the LD measurements have only limited usage (such as monitoring the change in particle size distribution over time) and should not be used directly for soil texture classification.
Varga et al. [55] also pointed out the lack of studies about the performance of commercially available LD devices. The authors further added that robustness, reproducibility, and comparability of grain size data obtained with various devices is a basic issue and associated uncertainties are rarely considered. Dumbrovský et al. [53], along with other authors, mentioned the possibility of LD analysis to calculate the results for any soil fraction classification. Of course, this can be done also for PM as there are various soil classification systems used worldwide, however the classification needs to be specified prior to the measurement because of different particle settling times. In case of LD, as the results are stored in the database, they can be recalculated post-measurement without the need of additional measurements. The only limitation for LD in this way is the measurement range. While in the past, due to the limited measuring range, LD had to be combined with another method of particle size distribution (such as sieving), it is not an issue nowadays as the devices reach the upper threshold of 2 mm. As the technology develops further, the measuring range of LD devices is extending up to 0.01–3000 µm in case of Mastersizer3000 with a Hydro Lv and Horiba Partica La-950 v 2 used in the study of Varga et al. [55]. We assume that the wide range of measurement and the short time of analysis (approximately 6 min for one cycle including cleaning) can also contribute to more accurate analyses, since more repetitive measurements can be done in considerably shorter time in comparison with sedimentation methods.

5. Conclusions

Determination of particle size distribution and the subsequent soil texture class is one of the most fundamental soil analyses. Although laser diffraction has a big potential in soil science applications, our study also confirmed the necessity of comparison with standard methods.
Our investigations focused on the particle size distribution of fractions according to simplified classification by Kachinski that was used in complex soil survey in former Czechoslovakia and comparison of the results. In total, 542 soil samples from two depths (15–20 cm and 40–45 cm) collected in Nitra, Hron, and Váh River basins in Slovakia were analyzed by pipette method and two state-of-the-art laser diffraction devices—Analysette22 MicroTec plus and Mastersizer2000.
We aimed especially at fraction <0.01 mm, because it is the fundamental fraction for soil texture determination in countries implementing the classification system of particle size fractions according to Kachinski and Novák’s classification of soil texture classes.
It was found that LD generally underestimated representation of fraction <0.001 mm and above 0.25 mm and overestimated representation of fractions <0.01 mm, <0.05 mm, and <0.25 mm. Considering one of the most common soil texture classification systems used in Slovakia (according to Novák), the emphasis was placed on the determination accuracy of particle size fraction <0.01 mm.
One of the most important findings of the study is the calculated conversion equations of LD results to PM recommended for estimation of the content of particle size fractions <0.001 mm, <0.01 mm, and <0.25 mm in case of Mastersizer2000 and <0.01 mm and <0.25 mm in the case of Analysette22. On the other hand, the same relationships are less suitable for estimation of particle size fractions (and fractions in their proximity) <0.05 mm and above 0.25 mm, and other approaches must be sought for reliable conversion of the representation from LD to PM. Moreover, according to the representation of soil texture classes in our soil sample dataset, the best fit is expected for medium heavy soils.
Considering the advantages of LD, it is necessary to work on developing a faster equivalent analysis method to standard pipette method (such as LD) that could potentially replace it in the future. Moreover, the attention should be paid to approaches of LD data conversion to PM or other standard sedimentation methods especially for light and heavy soils. Development of relationships related to other classifications of particle size fractions and soil texture classes commonly used worldwide can increase the comparability with other studies and contribute to building up the database of LD measurements around the world.

Supplementary Materials

The following are available online at https://www.mdpi.com/2073-4441/12/5/1232/s1, Figure S1: taking disturbed samples in the arable land during the field campaign, Figure S2: agricultural land in the Nitra River basin, Figure S3: agricultural land in the Váh River basin, Figure S4: agricultural land in the Hron River basin, Figure S5: particle size laser analyzer Analysette22 MicroTec plus (Fritsch, Germany), Figure S6: particle size laser analyzer Mastersizer2000 (Marlvern, UK), Figure S7: representation of the soil texture classes in the whole study area, Table S1: different classification systems of particle size fractions mentioned in this study, Table S2: percentage distribution of soil texture classes in the Nitra, Váh and Hron River basins, Slovakia according to Novák’s classification, Table S3: results on statistical analysis of cumulative percentage distribution of particle size fractions determined by pipette method.

Author Contributions

Conceptualization, D.I., E.A. and V.Š; methodology, D.I. and E.A.; investigation, D.I., E.A., M.Š., A.T. and J.H.; resources, D.I. and E.A.; data curation, D.I., E.A. and A.T.; writing—original draft preparation, M.Š. and D.I.; writing—review and editing, V.Š. and E.A., visualization, M.Š.; supervision, D.I.; funding acquisition, D.I. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the SCIENTIFIC GRANT AGENCY, grant number VEGA 1/0747/20 and VEGA 1/0064/19 and CULTURAL AND EDUCATIONAL GRANT AGENCY, grant number KEGA 026SPU-4/2017 and KEGA 019SPU-4/2020.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

References

  1. Bieganowski, A.; Ryżak, M.; Sochan, A.; Makó, A.; Barna, G.; Hernádi, H.; Beczek, M.; Polakowski, C. Laser diffractometry in the measurements of soil and sediment particle size distribution. Adv. Agron. 2018, 151, 215–279. [Google Scholar]
  2. Makó, A.; Szabó, B.; Rajkai, K.; Szabó, J.; Bakacsi, Z.; Labancz, V.; Hernádi, H.; Barna, G. Evaluation of soil texture determination using soil fraction data resulting from laser diffraction method. Int. Agrophys. 2019, 33, 445–454. [Google Scholar] [CrossRef]
  3. Yang, Y.; Wang, L.; Wendroth, O.; Liu, B.; Cheng, C.; Huang, T.; Shi, Y. Is the laser diffraction method reliable for soil particle size distribution analysis? Soil Sci. Soc. Am. J. 2019, 83, 276–287. [Google Scholar] [CrossRef]
  4. Fulajtár, E. Fyzikálne Vlastnosti Pôdy [Physical Properties of Soil], 1st ed.; VÚPOP: Bratislava, Slovakia, 2006. (In Slovak) [Google Scholar]
  5. Igaz, D.; Aydin, E.; Horák, J.; Čimo, J.; Tárník, A.; Bárek, V. Základné Merania v Hydropedológii [Basic Measurements in Hydropedology], 1st ed.; Slovak University of Agriculture: Nitra, Slovakia, 2017. (In Slovak) [Google Scholar]
  6. Šimanský, V.; Polláková, N.; Chlpík, J.; Kolenčík, M. Pôdoznalectvo [Soil Science], 1st ed.; Slovak University of Agriculture: Nitra, Slovakia, 2018. (In Slovak) [Google Scholar]
  7. Fotyma, M.; Igras, J.; Tkaczyk, P.; Pikuła, D. Soil testing methods and fertilizer recommendations in Central–Eastern European countries. Monography. Fertil. Fertil. 2008, 30, 1–110. Available online: http://nawfert.iung.pulawy.pl/zeszyty/pelne/30%202008.pdf (accessed on 14 April 2020).
  8. Bárek, V.; Halaj, P.; Igaz, D. The influence of climate change on water demands for irrigation of special plants and vegetables in Slovakia. In Bioclimatology and Natural Hazards; Springer: Dordrecht, The Netherlands, 2009; pp. 271–282. [Google Scholar]
  9. Tárník, A.; Igaz, D. Quantification of soil water storage available to plants in the Nitra river basin. Acta Sci. Pol. 2015, 14, 209–216. [Google Scholar] [CrossRef]
  10. Mikloš, M.; Igaz, D.; Šinka, K.; Škvareninová, J.; Jančo, M.; Vyskot, I.; Škvarenina, J. Ski piste snow ablation versus potential infiltration (Veporic Unit, Western Carpathians). J. Hydrol. Hydromech. 2020, 68, 28–37. [Google Scholar] [CrossRef] [Green Version]
  11. Gee, G.W.; Bauder, J.W. Particle-size analysis. In Methods of Soil Analysis, Part 1 Physical and Mineralogical Methods, 2nd ed.; Klute, A., Ed.; SSSA: Madison, WI, USA, 1986; pp. 383–409. [Google Scholar]
  12. Muggler, C.C.; Pape, T.; Buurman, P. Laser grain-size determination in soil genetic studies 2. Clay content, clay formation, and aggregation in some Brazilian oxisols. Soil Sci. 1997, 162, 219–228. [Google Scholar] [CrossRef]
  13. Lal, R.; Shukla, M.K. Principles of Soil Physics; Marcel Dekker: New York, NY, USA, 2004. [Google Scholar]
  14. Hrivňáková, K.; Makovníková, J.; Barančíková, G.; Bezák, P.; Bezáková, Z.; Dodok, R.; Grečo, V.; Chlpík, J. Jednotné Pracovné Postupy Rozborov Pôd [Uniform Working Procedures for Soil Analyzes]; VUPOP: Bratislava, Slovakia, 2011. (In Slovak) [Google Scholar]
  15. Soil Survey Staff. Soil Survey Field and Laboratory Methods Manual; Soil Survey Investigations Report No. 51, Version 2.0; Burt, R., Soil Survey Staff, Eds.; U.S. Department of Agriculture, Natural Resources Conservation Service: Lincoln, NE, USA, 2014. Available online: https://www.nrcs.usda.gov/Internet/FSE_DOCUMENTS/stelprdb1244466.pdf (accessed on 2 February 2020).
  16. Allen, T.A. Particle Size Measurement, 4th ed.; Chapman and Hall: London, UK, 1990. [Google Scholar]
  17. Vendelboe, A.L.; Moldrup, P.; Schjønning, P.; Oyedele, D.J.; Jin, Y.; Scow, K.M.; De Jonge, L.W. Colloid release from soil aggregates: Application of laser diffraction. Vadose Zone J. 2012, 11, 1539–1663. [Google Scholar] [CrossRef]
  18. Zumr, D.; Mützenberg, D.V.; Neumann, M.; Jeřábek, J.; Laburda, T.; Kavka, P.; Johannsen, L.L.; Zambon, N.; Klik, A.; Strauss, P.; et al. Experimental setup for splash erosion monitoring—Study of silty loam splash characteristics. Sustainability 2020, 12, 157. [Google Scholar] [CrossRef] [Green Version]
  19. Kondrlová, E.; Igaz, D.; Horák, J. Principles of soil particle size analysis by indirect optical method: Advantages and disadvantages of laser diffraction analysis. Mater. Methods Technol. 2013, 7, 492–501. [Google Scholar]
  20. Goossens, D.; Buck, B. Dust emission by off-road driving: Experiments on 17 arid soil types Nevada, USA. Geomorphology 2009, 107, 118–138. [Google Scholar] [CrossRef]
  21. Stanley, K.E.; Schaetzl, R.J. Characteristics and paleoenvironmental significance of a thin, dual-sourced loess sheet, north-central Wisconsin. Aeolian Res. 2011, 2, 241–251. [Google Scholar] [CrossRef]
  22. ISO 13320:2009 (BS ISO 13320:2009). Particle Size Analysis-Laser Diffraction Methods; International Organization for Standardization: Geneva, Switzerland, 2009. [Google Scholar]
  23. Vandecasteele, B.; De Vos, B. Relationship between soil textural fractions determined by the sieve-pipette method and laser diffractometry. IBW Bb R 2003, 1–19. Available online: https://www.researchgate.net/publication/273948901_Relationship_between_soil_textural_fractions_determined_by_the_sieve-pipette_method_and_laser_diffractometry (accessed on 14 April 2020).
  24. Šinkovičová, M.; Igaz, D.; Čimo, J.; Halaj, P. Preparation methodology of soil samples for laser diffraction. Mater. Methods Technol. 2016, 10, 191–197. [Google Scholar]
  25. Šinkovičová, M.; Igaz, D.; Kondrlová, E.; Jarošová, M. Soil particle size analysis by laser diffractometry: Result comparison with pipette method. IOP Conf. Ser. Mater. Sci. Eng. 2017, 245, 072025. [Google Scholar] [CrossRef]
  26. Kondrlová, E.; Igaz, D.; Grešová, L.; Horák, J. Porovnanie spôsobov prípravy pôdnych vzoriek a metód merania distribúcie zrnitostných frakcií pôd v povodí rieky Nitra [Comparison of methods of soil samples preparation and methods of measurement of grain size fractions of distribution in Nitra River basin]. Acta Hortic. Regiotect. 2012, 15, 27–30. (In Slovak) [Google Scholar]
  27. Kondrlová, E.; Igaz, D.; Horák, J.; Čimo, J. Comparison of sample preparation methods for laser diffraction to determine the particle size distribution of medium fine soils. In Proceedings of the Land Degradation and Challenges in Sustainable Soil Management: 8th International Soil Science Congress, Izmir, Turkey, 15–17 May 2012; pp. 432–437. [Google Scholar]
  28. Kun, Á.; Katona, O.; Sipos, G.; Barta, K. Comparison of pipette and laser diffraction methods in determining the granulometric content of fluvial sediment samples. J. Environ. Geogr. 2013, 6, 49–54. [Google Scholar] [CrossRef] [Green Version]
  29. Yang, X.; Zhang, Q.; Li, X.; Jia, X.; Wei, X.; Shao, M. Determination of soil texture by laser diffraction method. Soil Phys. Hydrol. Soil Sci. Soc. Am. J. 2015, 79, 1556–1566. [Google Scholar] [CrossRef] [Green Version]
  30. Taubner, H.; Roth, B.; Tippkötter, R. Determination of soil texture: Comparison of the sedimentation method and the laser-diffraction analysis. J. Plant Nutr. Soil Sci. 2009, 172, 161–171. [Google Scholar] [CrossRef]
  31. Mihalache, D.; Ilie, L.; Marin, D.I.; Calciu, I. The new methods for measuring soil texture. In Seria Agricultură-Montanologie-Cadastru; Analele Universităţii: Craiova, Romania, 2010; Volume 40, pp. 486–490. [Google Scholar]
  32. Jena, R.; Jagadeeswaran, R.; Sivasamy, R. Analogy of soil parameters in particle size analysis through laser diffraction techniques. Indian J. Hill Farm. 2013, 26, 78–83. [Google Scholar]
  33. Kondrlová, E.; Igaz, D.; Horák, J. Effect of calculation models on particle size distribution estimated by laser diffraction. J. Ege Univ. Fac. Agric. 2015, 52, 21–27. [Google Scholar]
  34. FRITSCH. Laser Equipment for Particle Analyzer 2016. Available online: http://www.ilabo.cz/UserFiles/File/eshop/672/d_ANALYSETTE%2022%20CZ.pdf (accessed on 1 February 2020).
  35. Kerry, R.; Rawlins, B.G.; Oliver, M.A.; Lacinska, A.M. Problems with determining the particle size distribution of chalk soil and some of their implications. Geoderma 2009, 152, 324–337. [Google Scholar] [CrossRef] [Green Version]
  36. Di Stefano, C.; Ferro, V.; Mirabile, S. Testing the grain-size distribution determined by laser diffractometry for sicilian soils. J. Agric. Eng. 2011, 42, 39–46. [Google Scholar] [CrossRef]
  37. Kowalenko, C.G.; Babuin, D. Inherent factors limiting the use of laser diffraction for determining particle size distributions of soil and related samples. Geoderma 2013, 193–194, 22–28. [Google Scholar] [CrossRef]
  38. Eshel, G.; Levy, G.J.; Mingelgrin, U.; Singer, M.J. Critical evaluation of the use of laser diffraction method for particle-size distribution analysis. Soil Sci. Am. J. 2004, 68, 736–743. [Google Scholar] [CrossRef]
  39. Soil Survey Staff. Soil Taxonomy: A Basic System of Soil Classification for Making and Interpreting Soil Surveys; Natural Resources Conservation Service: Washington, DC, USA, 2010. [Google Scholar]
  40. Bedrna, Z.; Ofránus, T. Aplikácia novej klasifikácie textúry v geografii pôd Slovenska. [Application of new soil texture classification in geography of Slovakia]. Geogr. J. 2013, 65, 161–169. (In Slovak) [Google Scholar]
  41. Balkovič, J.; Bedrna, Z.; Bublinec, E.; Čurlík, J.; Dlapa, P.; Fulajtár, E.; Gregor, J. Morfogenetický Klasifikačný Systém Pôd Slovenska. Bazálna Referenčná Taxonómia [Morphogenetic Soil Classification System of Slovakia], 2nd ed.; NPPC VÚPOP: Bratislava, Slovakia, 2014. (In Slovak) [Google Scholar]
  42. Gleboznawcze, P.T. Particle size distribution and textural classes of soils and mineral materials - classification of Polish Society of Soil Science 2008. Pol. Soil Sci. Annu. 2009, 60, 5–16. [Google Scholar]
  43. IUSS Working Group WRB. World Reference Base for Soil Resources 2014, Update 2015. International Soil Classification System for Naming Soils and Creating Legends for Soil Maps; World Soil Resources Reports No. 106; FAO: Rome, Italy, 2015. [Google Scholar]
  44. Hristov, B. The importance of soil texture in soil classification systems. J. Balk. Ecol. 2013, 16, 137–139. [Google Scholar]
  45. Deng, J.; Ma, C.; Yu, H. Different soil particle-size classification systems for calculating volume fractal dimension—A case study of Pinus sylvestris var. Mongolica in Mu Us Sandy Land, China. Appl. Sci. 2018, 8, 1872. [Google Scholar] [CrossRef] [Green Version]
  46. Ilavská, B. Využitie údajov VUPOP pri pozemkových úpravách. [Use of SSCRI Data for Land Consolidation]. In Workshop of Land Consolidation; SZG: Bratislava, Slovakia, 2001. (In Slovak) [Google Scholar]
  47. Petrovič, F.; Stranovsky, P.; Muchová, Z.; Falťan, V.; Skokanová, H.; Havlíček, M.; Gábor, M.; Spulerová, J. Landscape-ecological optimization of hydric potential in foothills region with dispersed settlements—A case study of Nová Bošáca, Slovakia. Appl. Ecol. Environ. Res. 2017, 15, 379–400. Available online: http://www.aloki.hu/pdf/1501_379400.pdf (accessed on 20 February 2020). [CrossRef]
  48. Súľovský, M.; Falťan, V.; Skokanová, H.; Havlíček, M.; Petrovič, F. Spatial analysis of long-term land-use development in regard to physiotopes: Case studies from the Carpathians. Phys. Geogr. 2017, 38, 470–488. [Google Scholar] [CrossRef]
  49. VÚMOP. Research Institute for Soil and Water Conservation, Praha: An Overview of Performance and Results Obtained in 1993 with a Short Account of History; Výzkumný Ústav Meliorací a Ochrany Půdy: Praha, Czech Republic, 1994. [Google Scholar]
  50. Šimanský, V.; Polláková, N.; Chlpík, J.; Kolenčík, M. Návody na Cvičenia z Pôdoznalectva [Guidelines for Soil Science Practicals]; Slovenská Poľnohospodárska Univerzita v Nitre: Nitra, Slovakia, 2017. (In Slovak) [Google Scholar]
  51. Skalová, J.; Kotorová, D.; Igaz, D.; Gomboš, M.; Nováková, K. Regionalizácia Pedotransferových Funkcií Vlhkostných Retenčných Kriviek Pôdy [Regionalization of Pedotransfer Functions of Soil Moisture Retention Curves]; STU: Bratislava, Slovakia, 2015. (In Slovak) [Google Scholar]
  52. Hydrophysics Web Server. 2020. Available online: http://fzki.uniag.sk/hydrophysics/ (accessed on 10 February 2020).
  53. Dumbrovský, M.; Larišová, L.; Sobotková, V.; Kulihová, M. Comparison of different texture analysis for soil erodibility calculations of loamy and sandy-loam soils in Moravian regions. Acta Univ. Agric. Silvic. Mendel. Brun. 2019, 67, 383–393. [Google Scholar] [CrossRef] [Green Version]
  54. Ließ, M.; Glaser, B.; Huwe, B. Uncertainty in the spatial prediction of soil texture. Comparison of regression tree and Random Forest models. Geoderma 2012, 170, 70–79. [Google Scholar] [CrossRef]
  55. Varga, G.; Gresina, F.; Újvári, G.; Kovács, J.; Szalai, Z. On the reliability and comparability of laser diffraction grain size measurements of paleosols in loess records. Sediment. Geol. 2019, 389, 42–53. [Google Scholar] [CrossRef]
  56. Orzechowski, M.; Smólczyński, S.; Długosz, J.; Poźniak, P. Measurements of texture of soils formed from glaciolimnic sediments by areometric method, pipette method and laser diffraction method. Sci. Annu. 2014, 65, 72–79. [Google Scholar] [CrossRef]
  57. Miller, B.A.; Schaetzl, R.J. Precision of soil particle analysis using laser diffractometry. Soil Sci. Am. J. 2011, 76, 1719–1727. [Google Scholar] [CrossRef] [Green Version]
  58. Konert, M.; Vandenberghe, J. Comparison of laser grain size analysis with pipette and sieve analysis: A solution for the underestimation of the clay fraction. Sedimentology 1997, 44, 523–535. [Google Scholar] [CrossRef] [Green Version]
  59. Beuselinck, L.; Govers, G.; Poesen, J.; Degraer, G.; Froyen, L. Grain-size analysis by laser diffractometry: Comparison with the sieve-pipette method. Catena 1998, 32, 193–208. [Google Scholar] [CrossRef]
  60. Sochan, A.; Bieganowski, A.; Ryżak, M.; Dobrowolski, R.; Bartmiñski, P. Comparison of soil texture determined by two dispersion units of Mastersizer 2000. Int. Agrophys. 2012, 26, 99–102. [Google Scholar] [CrossRef]
Water 12 01232 g001 550
Figure 1. Location and the number of sampling sites in the Nitra, Váh, and Hron River basins [52].
Figure 1. Location and the number of sampling sites in the Nitra, Váh, and Hron River basins [52].
Water 12 01232 g001
Water 12 01232 g002 550
Figure 2. Comparison of cumulative particle size fractions representation determined by Analysette22 MicroTec plus (LD_22) and Mastersizer2000 (LD_2000) and pipette method (PM) for soil samples from three river basins. LD, laser diffraction.
Figure 2. Comparison of cumulative particle size fractions representation determined by Analysette22 MicroTec plus (LD_22) and Mastersizer2000 (LD_2000) and pipette method (PM) for soil samples from three river basins. LD, laser diffraction.
Water 12 01232 g002
Water 12 01232 g003 550
Figure 3. Linear regression correlation between pipette method (PM) and laser diffraction method for all soil samples as determined by Analysette22 MicroTec plus (LD_22) and Mastersizer2000 (LD_2000).
Figure 3. Linear regression correlation between pipette method (PM) and laser diffraction method for all soil samples as determined by Analysette22 MicroTec plus (LD_22) and Mastersizer2000 (LD_2000).
Water 12 01232 g003
Water 12 01232 g004 550
Figure 4. Exponential regression correlation between pipette method (PM) and laser diffraction method for all soil samples as determined by Analysette22 MicroTec plus (LD_22) and Mastersizer2000 (LD_2000).
Figure 4. Exponential regression correlation between pipette method (PM) and laser diffraction method for all soil samples as determined by Analysette22 MicroTec plus (LD_22) and Mastersizer2000 (LD_2000).
Water 12 01232 g004
Water 12 01232 g005 550
Figure 5. Polynomial regression correlation between pipette method (PM) and laser diffraction method for all soil samples as determined by Analysette22 MicroTec plus (LD_22) and Mastersizer2000 (LD_2000).
Figure 5. Polynomial regression correlation between pipette method (PM) and laser diffraction method for all soil samples as determined by Analysette22 MicroTec plus (LD_22) and Mastersizer2000 (LD_2000).
Water 12 01232 g005
Table
Table 1. Classification of soil texture classes according to Novák [50].
Table 1. Classification of soil texture classes according to Novák [50].
Particles with Diameter ˂0.01 mm (% Mass)Soil Texture ClassGeneral Soil Texture Class
<10Sandy soilLight soils
10–20Loam-sandy soil
20–30Sand-loamy soilMedium heavy soils
30–45Loamy soil
45–60Clay-loamy soilHeavy soils
60–75Clay soil
>75Clay
Table
Table 2. Statistical verification of the regression models with the highest determination coefficient, R2 (n = 271).
Table 2. Statistical verification of the regression models with the highest determination coefficient, R2 (n = 271).
TrendDetermination Coefficient R2 (%)Statistical Significance FConstant (p-Value for Intercept)Regression Coefficient (p-Value for X Variables)
Analysette22 (LD_22)Linear72.69000
Exponential70.34000
Polynomial76.6400b1 = 0.0342; b2 = 0
Mastersizer2000 (LD_2000)Linear81.34000
Exponential75.87000
Polynomial84.6700b1 = 0.0218; b2 = 0
Table
Table 3. Verification of the results. Differences (%) between calculated estimated values using laser diffraction and different regression models (PMestLM, PMestEM, and PMestPM) and originally measured PM values (PMme) present as mean values ± standard error.
Table 3. Verification of the results. Differences (%) between calculated estimated values using laser diffraction and different regression models (PMestLM, PMestEM, and PMestPM) and originally measured PM values (PMme) present as mean values ± standard error.
Fractions<0.001 mm<0.01 mm<0.05 mm<0.25 mm<2 mm
Analysette22 (LD_22)PMestLM 1–PMme 2−0.75 ± 0.5914.99 ± 0.8611.23 ± 0.93−3.80 ± 0.84−15.11 ± 0.02
PMestEM 3–PMme−1.05 ± 0.582.31 ± 0.828.56 ± 1.02−3.08 ± 0.88−14.00 ± 0.04
PMestPM 4–PMme5.18 ± 0.583.28 ± 0.8210.87 ± 1.02−0.98 ± 0.88−11.91 ± 0.04
Mastersizer2000 (LD_2000)PMestLM–PMme−4.28 ± 0.5811.43 ± 0.848.29 ± 0.80−1.06 ± 0.72−10.89 ± 0.00
PMestEM–PMme−1.92 ± 0.58−0.79 ± 0.802.25 ± 0.900.95 ± 0.85−6.16 ± 0.00
PMestPM–PMme1.94 ± 0.582.24 ± 0.805.10 ± 0.881.36 ± 0.81−6.61 ± 0.00
1 calculated from LD, linear model, 2 measured by pipette method, 3 calculated from LD, exponential model, 4 calculated from LD, polynomial model.

Share and Cite

MDPI and ACS Style

Igaz, D.; Aydin, E.; Šinkovičová, M.; Šimanský, V.; Tall, A.; Horák, J. Laser Diffraction as An Innovative Alternative to Standard Pipette Method for Determination of Soil Texture Classes in Central Europe. Water 2020, 12, 1232. https://doi.org/10.3390/w12051232

AMA Style

Igaz D, Aydin E, Šinkovičová M, Šimanský V, Tall A, Horák J. Laser Diffraction as An Innovative Alternative to Standard Pipette Method for Determination of Soil Texture Classes in Central Europe. Water. 2020; 12(5):1232. https://doi.org/10.3390/w12051232

Chicago/Turabian Style

Igaz, Dušan, Elena Aydin, Miroslava Šinkovičová, Vladimír Šimanský, Andrej Tall, and Ján Horák. 2020. "Laser Diffraction as An Innovative Alternative to Standard Pipette Method for Determination of Soil Texture Classes in Central Europe" Water 12, no. 5: 1232. https://doi.org/10.3390/w12051232

APA Style

Igaz, D., Aydin, E., Šinkovičová, M., Šimanský, V., Tall, A., & Horák, J. (2020). Laser Diffraction as An Innovative Alternative to Standard Pipette Method for Determination of Soil Texture Classes in Central Europe. Water, 12(5), 1232. https://doi.org/10.3390/w12051232

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop