1. Introduction
Electrospinning is a technique utilizing high-voltage (HV) electric fields to produce nanofibrous materials from polymer solutions or, less commonly, polymer melts [
1]. In the electrospinning device (for a schematics see
Figure 1), the strong electric field destabilizes the surface of the liquid connected to a terminal of a high-voltage power supply, and the liquid subsequently forms a pointed meniscus, the Taylor cone. A discharge in the form of a thin liquid jet then emanates from the tip of the cone. The liquid jet is not always stable and may disintegrate into liquid aerosol leading to an electrospray, which is itself an important phenomenon in applied physics [
2,
3]. When the jet arrives at the counter-electrode, a collector, it deposits as a solid nanofiber. In the case of solution spinning (which is the most common one), solidification is facilitated by rapid evaporation of the solvent. Bending, or whipping, instability occurring after a short linear path of the jet significantly contributes to elongation and thinning of the jet [
4,
5]. By depositing many layers of nanofibers, a non-woven fabric is created on the collector showing exceptional porosity and surface-area-to-volume ratio [
6]. Owing to their unique properties and versatility of their preparation, electrospun nanofabrics find a wide variety of applications, such as air filtration [
7,
8], oil/water separation [
9], drug delivery [
10,
11], or tissue engineering [
12]. With the outbreak of the novel coronavirus pandemic (COVID-19) in 2020, electrospun materials have gained attention as a promising active layer for protective face masks [
13].
The theoretical description of electrospinning and related phenomena has predominantly relied on electrohydrodynamic models formulated within continuum mechanics [
5,
15,
16]. The fundamentals of theoretical understanding of the field-induced phenomena at liquid interfaces related to electrospray and electrospinning were laid by Lord Rayleigh [
17], John Zeleny [
18], and most notably sir Geoffrey Ingram Taylor [
19,
20,
21], who studied a conical formation occurring on liquid surfaces in strong electric fields, the formation which today bears his name: the Taylor cone. Conventional electrohydrodynamic approach to weakly conducting fluids in electric fields, the Taylor–Melcher leaky dielectric model [
16], incorporates both dielectric polarization and ionic conduction in terms of the Maxwell stress tensor and conservation equations. If the charge relaxation time,
, is much lower than the hydrodynamic relaxation time,
, the behavior of a leaky dielectric liquid approaches that of a perfect conductor, and when the opposite is true, i.e.,
, the liquid behaves as an insulator. The former situation is assumed to take place when the Taylor cone builds, whereas the latter is believed to exist in a flying jet [
5]. For a modern review on continuum modeling of electrospinning, we refer the reader to the monograph of Ko and Wan [
22] or the chapter by Rafiei [
23].
Apart from the conventional continuum modeling one can also find reports on methods involving discrete macro- or mesoscopic elements. The entire jet can be modeled as a chain of charged particles connected by visco-elastic links with one another as, e.g., in works of Reneker et al. [
4] or Lauricella et al. [
24,
25]. Mesoscopic modeling incorporating individual polymer chains was performed by Liu et al. [
26,
27,
28,
29], who employed the dissipative particle dynamics to model polymer melt electrospinning using a coarse-grained model of chains. The dissipative particle dynamics was also applied by Joulaian et al. [
30] to model the initial stages of the formation of the Taylor cone.
Truly atomistic simulations of electrospinning with explicit solvent are scarce in the literature. Jirsák et al. published several works [
31,
32,
33,
34,
35] developing and applying an approach to model electrospinning by atomistic molecular simulations in several geometries of the simulation cell using the rigid water model, simple sodium chloride ions and model poly(ethylene glycol) (PEG) chains. Jirsák et al. concluded that even a perfect dielectric (model water) was able to jet in electric field and revealed a link between liquid jetting and bridging. In a similar, independent study, Wang et al. [
36] investigated the behavior of a polymer solution droplet in the electric field and the influence of ions on spinnability.
The above-mentioned previous works [
31,
32,
33,
34,
35] co-authored by the first author represent a continuing effort to tackle the atomistic modeling of electrospinning methodologically and to understand the process on a fundamental, molecular level. In the first article [
31], Jirsák et al. partitioned the process of electrospinning into zones accessible to modeling (free liquid surface, the tip of the Taylor cone, and the linear segment of the liquid jet) and proposed several strategies for implementation of molecular simulation in the respective zones. Application of the developed methodology to pure water and aqueous sodium chloride revealed that at atomic scale ions play only a marginal role in jet initiation; nevertheless, their presence destabilizes the jet. In the subsequent paper [
32], the authors noticed an interesting analogy between the liquid jet in electrospinning and a cylindrical structure created by water in electric field, the ‘floating water bridge’ [
37]. In paper [
33], the authors further investigated the influence of ions on the stability of field-induced liquid cylinders, monitored the mass flow in jets and added a model of polymer to the system (PEG). In Ref. [
34], Jirsák et al. analyzed polymer conformation and solvation during jetting. They concluded that polymer chains unfolded when entering the jet and that they remained well solvated despite progressing fragmentation of the solvent. The invited chapter [
35] presented an comprehensive overview of the developed methodology and summarized the achieved results.
In the present contribution, the authors work further towards understanding the molecular mechanism of electrospinning, especially its initial stages: formation of the Taylor cone and the onset of jetting. Following the methodology developed earlier [
31,
32,
33,
34,
35], systematic simulations of saline aqueous solutions of PEG are performed and analyzed with respect to a wide range of dynamic and structural properties. Unlike the previous studies, the present work adds laboratory experiments performed on the solutions of composition comparable to that used in simulations. An oscilloscopic method developed by P. Pokorný and coworkers at the Technical University of Liberec [
38,
39] is used to measure the latency time before the first Taylor cone builds and discharges.
The remaining part of the article is organized as follows. In the next section, methods utilized in molecular simulations and experiments are described along with all parameters necessary for reproduction. The following section, Results and Discussion, compiles the data produced by simulations and experiments, offers the interpretation of the data, and finally discusses how molecular and macroscopic observations might be related. Limitations of the present study are also discussed. The last section, Conclusions, summarizes main findings of the work and outlines challenges for future research.
4. Conclusions
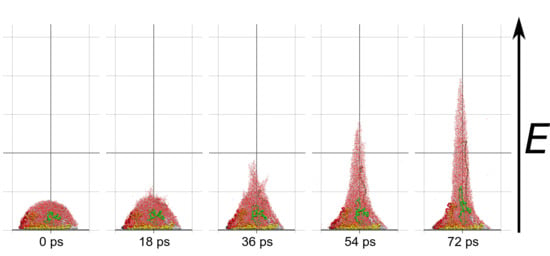
Molecular dynamics simulations of a nanosized droplet of polymer solution subjected to strong electric fields were performed. Formation of the Taylor cone and subsequent jetting accompanied by rapid evaporation of solvent was observed. The results indicate that at molecular scale, the formation of the cone and the onset of jetting is governed by dielectric forces, in apparent contrast with macroscopic continuum models. Ions do not significantly affected the nature of the process but facilitated the transport of polymer chains into the jet and enhanced the evaporation of solvent.
Experiments were performed with similar composition of solutions as in the simulations. A weaker-than-expected effect of ions on the time of formation of the Taylor cone was found—onset times slightly decreased with increasing ionic concentration, with the exception of the highest polymer concentration where no trend was discernible. High-speed photographs show that the solution did not actually spin, which was expected. The observations are consistent with electrospray in different modes (corona discharge, cone–jet, spindle). There is not enough data to assess the effect of ions on the morphology of the process.
Apparent discord between governing mechanisms, i.e., conductive in macroscale models vs. dielectric in molecular models might be upsetting, but creates an opportunity to grasp better understanding of the underlying physics in its full complexity. Simple considerations on the time and length scales involved in experiments and in simulations might bring a relief that there is nothing fundamentally wrong with either, but only after attempting to bridge the vast space between nano- and macroscale we may truly learn something new. That is the path the present authors strive to follow in future research.