Water Purification from Heavy Metals Due to Electric Field Ion Drift
Abstract
:1. Introduction
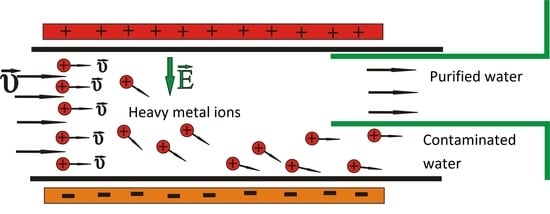
2. Materials and Methods
- (1)
- Two electrodes charged by a voltage V, producing between them an almost homogeneous and constant electric field with direction going from positive to negative;
- (2)
3. General Study of the Final State for the Stern Model
3.1. Boundary Conditions
3.2. Accurate Solution for the Final State
3.3. Validity of the Model
4. PNP Equations for the Stern Model
4.1. Linearized Solution of the PNP Equations
4.2. Long Time Behavior of the Linearized Approximation
4.3. Time Prediction with the Linear Approach
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Concentration | mole/m3 | |
| D | Diffusion coefficient | /s |
| J | Ionic flux | |
| i | Current density | |
| T | Absolute temperature | K |
| z | Number of overflow protons or electrons | |
| E | Electric field intensity | V/m |
| y | y axis coordinate | m |
| L | Width of the duct | m |
| c | Capacity | F |
| t | Time | s |
| Greek symbols | ||
| electric permittivity | F/m | |
| φ | Electric potential | V |
| ρ | Charge density | |
| ν | Dymanic viscocity | Pa s |
| σ | Surface charge density | C/m2 |
| μ | Mobility | s/Kg |
| τ | Time constant | s |
| Width of Stern layer | m | |
| λ | Width of the diffuse layer | m |
| α | Ion size | m |
| Subscripts | ||
| y | Along y axis | |
| bef | Before | |
| after | After | |
| M | Middle | |
| Constants | ||
References
- Bakarat, Μ.A. New trents in removing heavy metals from industrial wastewater. Arab. J. Chem. 2011, 4, 361–377. [Google Scholar] [CrossRef] [Green Version]
- Babel, S.; Kurniawan, T.A. Low-cost adsorbents for heavy metals uptake from contaminated water: A review. J. Hazard. Mater. 2003, B97, 219–243. [Google Scholar] [CrossRef]
- Babel, S.; Kurniawan, T.A. Various treatment technologies to remove arsenic and mercury from contaminated groundwater: An overview. In Proceedings of the First International Symposium on Southeast Asian Water Environment, Bangkok, Thailand, 24–25 October 2003; pp. 433–440. [Google Scholar]
- Babel, S.; Kurniawan, T.A. Cr (VI) removal from synthetic wastewater using coconut shell charcoal and commercial activated carbon modified with oxidizing agents and/or chitosan. Chemosphere 2004, 54, 951–967. [Google Scholar] [CrossRef] [PubMed]
- Alves-Junior, C.; Rodrigues-Junior, F.E.; Vitoriano, J.O.; Barauna, J.B.F.O. Investigating the Influence of the Pulsed Corona Discharge over Hypersaline Water. Mater. Res. 2021, 24, e20210261. [Google Scholar] [CrossRef]
- Abdelmoaty, H.M.; Mahgoub, A.U.; Abdeldayem, A.W. Performance analysis of salt reduction levels in indirect freeze desalination system with and without magnetic field exposure. Desalination 2021, 508, 115021. [Google Scholar] [CrossRef]
- Wang, L.K.; Vaccari, D.A.; Li, Y.; Shammas, N.K. Chemical Precipitation Physicochemical Treatment Processes; Humana Press: Totowa, NJ, USA, 2004; Volume 3, pp. 141–198. [Google Scholar]
- Aziz, H.A.; Adlan, M.N.; Ariffin, K.S. Heavy metals (Cd, Pb, Zn, Ni, Cu and Cr (III)) removal from water in Malaysia: Post treatment by high quality limestone. Bioresour. Technol. 2008, 99, 1578–1583. [Google Scholar] [CrossRef] [PubMed]
- Igwe, J.C.; Ogunewe, D.N.; Abia, A.A. Competitive adsorption of Zn (II), Cd (II) and Pb(II) ions from aqueous and non-aqueous solution by maize cob and husk. Afr. J. Biotechnol. 2005, 4, 1113–1116. [Google Scholar]
- Ajmal, M.; Rao, R.; Ahmad, R.; Ahmad, J. Adsorption studies on Citrus reticulata (fruit peel of orange) removal and recovery of Ni (II) from electroplating wastewater. J. Hazard. Mater. 2000, 79, 117–131. [Google Scholar] [CrossRef]
- Bansode, P.R.; Losso, J.N.; Marshall, W.E.; Rao, R.M.; Portier, R.J. Adsorption of metal ions by pecan shell-based granular activated carbons. Bioresour. Technol. 2003, 89, 115–119. [Google Scholar] [CrossRef]
- Tang, P.; Lee, C.K.; Low, K.S.; Zainal, Z. Sorption of Cr (VI) and Cu(II) in aqueous solution by ethylenediamine modified rice hull. Environ. Technol. 2003, 24, 1243–1251. [Google Scholar] [CrossRef] [PubMed]
- Fenga, D.; Aldrich, C. Adsorption of heavy metals by biomaterials derived from the marine alga Ecklonia maxima. Hydrometallurgy 2004, 73, 1–10. [Google Scholar] [CrossRef]
- Uysal, M.; Ar, I. Removal of Cr (VI) from industrial wastewaters by adsorption: Part I: Determination of optimum conditions. J. Hazard. Mater. 2007, 149, 482–491. [Google Scholar] [CrossRef] [PubMed]
- Deliyanni, E.A.; Peleka, E.N.; Matis, K.A. Removal of zinc ion from water by sorption onto iron-based nanoadsorbent. J. Hazard. Mater. 2007, 141, 176–184. [Google Scholar] [CrossRef] [PubMed]
- Barakat, M.A. Adsorption behavior of copper and cyanide ions at TiO2–solution interface. J. Colloid Interface Sci. 2005, 291, 345–352. [Google Scholar] [CrossRef]
- Bose, P.; Bose, M.A.; Kumar, S. Critical evaluation of treatment strategies involving adsorption and chelation for wastewater containing copper, zinc, and cyanide. Adv. Environ. Res. 2002, 7, 179–195. [Google Scholar] [CrossRef]
- Barakat, M.A. Adsorption of heavy metals from aqueous solutions on synthetic zeolite. Res. J. Environ. Sci. 2008, 2, 13–22. [Google Scholar]
- Solenera, M.; Tunalib, S.; Ozcan, A.S.; Ozcanc, A.; Gedikbey, T. Adsorption characteristics of lead (II) ions onto the clay/poly(methoxyethyl) acrylamide (PMEA) composite from aqueous solutions. Desalination 2008, 223, 308–322. [Google Scholar] [CrossRef]
- Crini, G. Recent developments in polysaccharide-based materials used as adsorbents in wastewater treatment. Prog. Polym. Sci. 2005, 30, 38–70. [Google Scholar] [CrossRef]
- Lee, S.T.; Mi, F.L.; Shen, Y.J.; Shyu, S.S. Equilibrium and kinetic studies of copper (II) ion uptake by chitosan–tripolyphosphate chelating resin. Polymer 2001, 42, 1879–1892. [Google Scholar] [CrossRef]
- Kurniawan, T.A.; Chan, G.Y.S.; Lo, W.H.; Babel, S. Physicochemical treatment techniques for wastewater laden with heavy metals. Chem. Eng. J. 2006, 118, 83–98. [Google Scholar] [CrossRef]
- Vigneswaran, S.; Ngo, H.H.; Chaudhary, D.S.; Hung, Y.T. Physico-chemical treatment processes for water reuse. In Physicochemical Treatment Processes; Humana Press: Totowa, NJ, USA, 2004; Volume 3, pp. 635–676. [Google Scholar]
- Juang, R.S.; Shiau, R.C. Metal removal from aqueous solutions using chitosan-enhanced membrane filtration. J. Membr. Sci. 2000, 165, 159–167. [Google Scholar] [CrossRef]
- Saffaj, N.; Loukil, H.; Younssi, S.A.; Albizane, A.; Bouhria, M.; Persin, M.; Larbot, A. Filtration of solution containing heavy metals and dyes by means of ultrafiltration membranes deposited on support made of Morrocan clay. Desalination 2004, 168, 301–306. [Google Scholar] [CrossRef]
- Cohen-Tanugi, D.; Grossman, J. Water Desalination across Nanoporous Graphene. Nano Lett. 2012, 12, 3602–3608. [Google Scholar] [CrossRef] [PubMed]
- Lv, J.; Wang, K.Y.; Chung, T.S. Investigation of amphoteric polybenzimidazole (PBI) nanofiltration hollow fiber membrane for both cation and anions removal. J. Membr. Sci. 2008, 310, 557–566. [Google Scholar] [CrossRef]
- Khedr, M.G. Membrane methods in tailoring simpler, more efficient, and cost effective wastewater treatment alternatives. Desalination 2008, 222, 135–145. [Google Scholar] [CrossRef]
- Abu Qdaisa, H.; Moussab, H. Removal of heavy metals from wastewater by membrane processes: A comparative study. Desalination 2004, 164, 105–110. [Google Scholar] [CrossRef]
- Telles, I.; Levin, Y.; Santos, A. Reversal of Electroosmotic Flow in Charged Nanopores with Multivalent Electrolyte. Langmuir 2022, 38, 3817–3823. [Google Scholar] [CrossRef] [PubMed]
- Skubal, L.R.; Meshkov, N.K.; Rajh, T.; Thurnauer, M. Cadmium removal from water using thiolactic acid-modified titanium dioxide nanoparticles. J. Photochem. Photobiol. A Chem. 2002, 148, 393–397. [Google Scholar] [CrossRef]
- Herrmann, J.M. Heterogeneous photocatalysis: Fundamentals and applications to the removal of various types of aqueous pollutants. Catal. Today 1999, 53, 115–129. [Google Scholar] [CrossRef]
- Zhang, F.S.; Itoh, H. Photocatalytic oxidation and removal of arsenite from water using slag–iron oxide–TiO2 adsorbent. Chemosphere 2006, 65, 125–131. [Google Scholar] [CrossRef]
- Barakat, M.A.; Chen, Y.T.; Huang, C.P. Removal of toxic cyanide and Cu (II) ions from water by illuminated TiO2 catalyst. J. Appl. Catal. B Environ. 2004, 53, 13–20. [Google Scholar] [CrossRef]
- Pedersen, A.J. Characterization and electrolytic treatment of wood combustion fly ash for the removal of cadmium. Biomass Bioenergy 2003, 25, 447–458. [Google Scholar] [CrossRef]
- Chen, G.H. Electrochemicals technologies in wastewater treatment. Sep. Purif. Technol. 2004, 38, 11–41. [Google Scholar] [CrossRef]
- Tzanetakis, N.; Taama, W.M.; Scott, K.; Jachuck, R.J.J.; Slade, R.S.; Varcoe, J. Comparative performance of ion exchange membrane for electrodialysis of nickel and cobalt. Sep. Purif. Technol. 2003, 30, 113–127. [Google Scholar] [CrossRef]
- Mohammadi, T.; Razmi, A.; Sadrzadeh, M. Effect of operating parameters on Pb2+ separation from wastewater using electrodialysis. Desalination 2004, 167, 379–385. [Google Scholar] [CrossRef]
- Jakobsen, M.R.; Rasmussen, J.F.; Nielsen, S.; Ottosen, L.M. Electrodialytic removal of cadmium from wastewater sludge. J. Hazard. Mater. 2004, 106, 127–132. [Google Scholar] [CrossRef] [PubMed]
- Al-Amshaweea, S.; Yunus, M.; Azoddeina, A.; Hassell, D.; Dakhil, I.; Hasan, H. Electrodialysis desalination for water and wastewater: A review. Chem. Eng. J. 2020, 380, 122231. [Google Scholar] [CrossRef]
- Oliveira, M.; Torres, I.; Ruggeri, H.; Scalize, P.; Albuquerque, A.; Gil, E. Application of Electrocoagulation with a New Steel-Swarf-Based Electrode for the Removal of Heavy Metals and Total Coliforms from Sanitary Landfill Leachate. Appl. Sci. 2021, 11, 5009. [Google Scholar] [CrossRef]
- Kim, T.; Kim, T.-K.; Zoh, K. Removal mechanism of heavy metal (Cu, Ni, Zn, and Cr) in the presence of cyanide during electrocoagulation using Fe and Al electrodes. J. Water Process Eng. 2020, 33, 101109. [Google Scholar] [CrossRef]
- Qasem, N.; Mohammed, R.; Lawal, D. Removal of heavy metal ions from wastewater: A comprehensive and critical review. Npj Clean Water 2021, 4, 1–5. [Google Scholar] [CrossRef]
- Pretorius, W.A.; Johannes, W.G.; Lempert, G.G. Electrolytic iron flocculant production with a bipolar electrode in series arrangement. Water SA 1991, 17, 133–138. [Google Scholar]
- Yang, X.; Liu, L.; Tan, W.; Qiu, G.; Liu, F. High-performance Cu2+ adsorption of birnessite using electrochemically controlled redox reactions. J. Hazard. Mater. 2018, 354, 107–115. [Google Scholar] [CrossRef] [PubMed]
- Jin, W.; Fu, Y.; Hu, M.; Wang, S.; Liu, Z. Highly efficient SnS-decorated Bi2O3 nanosheets for simultaneous electrochemical detection and removal of Cd(II) and Pb(II). J. Electroanal. Chem. 2020, 856, 113744. [Google Scholar] [CrossRef]
- Baghban, E.; Mehrabani-Zeinabad, A.; Moheb, A. The effects of operational parameters on the electrochemical removal of cadmium ion from dilute aqueous solutions. Hydrometallurgy 2014, 149, 97–105. [Google Scholar] [CrossRef]
- Dabrowski, A.; Hubicki, Z.; Podkościelny, P.; Robens, E. Selective removal of the heavy metal ions from waters and industrial wastewaters by ion-exchangemethod. Chemosphere 2004, 56, 91–106. [Google Scholar] [CrossRef] [PubMed]
- Tenório, J.A.; Espinosa, D. Treatment of chromium plating process effluents with ion exchange resins. Waste Manag. 2001, 21, 637–642. [Google Scholar] [CrossRef]
- Bartzis, V.; Sarris, I.E. A theoretical model for salt ion drift due to electric field suitable to seawater desalination. Desalination 2020, 473, 114163. [Google Scholar] [CrossRef]
- Bartzis, V.; Sarris, I.E. Electric field distribution and diffuse layer thickness study due to salt ion movement in water desalination. Desalination 2020, 490, 114549. [Google Scholar] [CrossRef]
- Sofos, F.; Karakasidis, T.; Spetsiotis, D. Molecular dynamics simulations of ion separation in nano-channel water flows using an electric field. Mol. Simul. 2019, 45, 1395–1402. [Google Scholar] [CrossRef]
- Sofos, F.; Karakasidis, T.; Sarris, I. Effects of channel size, wall wettability, and electric field strength on ion removal from water in nanochannels. Sci. Rep. 2022, 12, 641. [Google Scholar] [CrossRef] [PubMed]
- Sofos, F. A Water/Ion Separation Device: Theoretical and Numerical Investigation. Appl. Sci. 2021, 11, 8548. [Google Scholar] [CrossRef]
- Atkins, P.; Paola, J. Atkin’s Physical Chemistry, 8th ed.; Oxford University Press: Oxford, UK, 2006; Volume 5, pp. 136–169. [Google Scholar]
- Mortimer, R.G. Physical Chemistry, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2008; Volume 8, pp. 351–378. [Google Scholar]
- Brett, C.A.; Arett, A. Electrochemistry Principles, Methods, and Applications; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Debye, P.; Hückel, E. The theory of electrolytes. I. Lowering of freezing point and related phenomena. Phys. Z. 1923, 24, 185–206. [Google Scholar]
- Bonnefont, A.; Argoul, F.; Bazant, M. Analysis of diffuse layer on time-dependent interfacial kinetics. J. Electroanal. Chem. 2001, 500, 52. [Google Scholar] [CrossRef]
- Bazant, M.; Thornton, K.; Ajdari, A. Diffuse-charge dynamics in electrochemical systems. Phys. Rev. E 2004, 70, 021506. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Biesheuvel, P.M.; Porada, S.; Dykstra, J.E. The difference between Faradaic and Nonfaradaic processes in Electrochemistry. arXiv 2018, arXiv180902930v4. [Google Scholar]
- Bartzis, V.; Sarris, I.E. Time Evolution Study of the Electric Field Distribution and Charge Density Due to Ion Movement in Salty Water. Water 2021, 13, 2185. [Google Scholar] [CrossRef]
- Kilic, M.S.; Bazant, M.Z.; Ajdari, A. Steric effects in the dynamics of electrolytes at large applied voltages. I. Double-layer charging. Phys. Rev. E 2007, 75, 021502. [Google Scholar] [CrossRef] [Green Version]










Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bartzis, V.; Ninos, G.; Sarris, I.E. Water Purification from Heavy Metals Due to Electric Field Ion Drift. Water 2022, 14, 2372. https://doi.org/10.3390/w14152372
Bartzis V, Ninos G, Sarris IE. Water Purification from Heavy Metals Due to Electric Field Ion Drift. Water. 2022; 14(15):2372. https://doi.org/10.3390/w14152372
Chicago/Turabian StyleBartzis, Vasileios, Georgios Ninos, and Ioannis E. Sarris. 2022. "Water Purification from Heavy Metals Due to Electric Field Ion Drift" Water 14, no. 15: 2372. https://doi.org/10.3390/w14152372
APA StyleBartzis, V., Ninos, G., & Sarris, I. E. (2022). Water Purification from Heavy Metals Due to Electric Field Ion Drift. Water, 14(15), 2372. https://doi.org/10.3390/w14152372