Studying a Multi-Stage Flash Brine Recirculation (MSF-BR) System Based on Energy, Exergy and Exergoeconomic Analysis
Abstract
:1. Introduction
2. System Description
3. Modeling
- The latent heat of evaporation and condensation is assumed constant.
- The distillate water is salt-free.
- The variations in boiling temperature of brine at the recovery section outlet are small.
- Pressure and temperature are assumed to be constant in each stage.
- The heat capacity of brine is considered equal to that of distillate water at the same temperature.
- The heat transfer to surroundings is neglected.
- The pressure drop is negligible.
3.1. Energy Analysis
3.2. Exergy Analysis
3.3. Exeregoeconomic Analysis
4. Validation
5. Results and Discussion
5.1. Effect of TBT
5.2. Effect of Number of Stages
5.3. Exergoeconomic Analysis Results
6. Conclusions
- With increasing the top brine temperature, the exergy efficiency, gained output ratio (GOR) and distillate water production increase by 34%, 47% and 47% respectively.
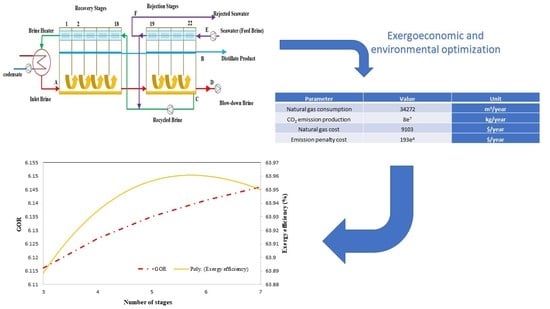
- With increasing the number of stages in the heat recovery section, GOR and distillate water production increase while the exergy efficiency decreases.
- With increasing the number of stages in the heat rejection section, distillate water production increases while GOR firstly increases and then decreases. Thus, the optimal number of stages in the heat rejection section is six stages.
- The relative cost difference increases by 94% with increasing the stage number.
- With increasing the stage number, the exergoeconomic factor firstly decreases and then increases.
- By utilizing the waste heat of the refinery complex as heating steam, 9103 $/year energy cost savings and 193 × 104 $/year emission penalty cost savings are obtained.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| MSF | Multi-stage flash | Subscript | |
| MSF-BR | Multi-stage flash with brine recycle | P | Pump |
| MED | Multi-effect desalination | HEX | Heat exchanger efficiency |
| GOR | Gain output ratio | In | Input |
| RO | Reverse osmosis | Fg | Vaporization condition |
| ED | Electro dialyze | Sat | Saturation |
| T | Temperature (°C) | Out | Output |
| P | Pressure (kPa) | Br | Brine |
| Q | Thermal energy (kW) | Eq | Equilibrium |
| M | Mass flow rate (kg/s) | St | Stage |
| h | Enthalpy (kJ/kg) | s | Steam produce |
| A | Area (m2) | ex | Exergy |
| Ex | Exergy (kW) | cv | Control volume |
| W | Work (kJ) |
References
- Dashtebayaz, M.D.; Fizik, A.E.; Namanlo, S.V. Energy and exergy analyses of using natural gas compressor station waste heat for cogeneration power and fresh water. Int. J. Exergy 2019, 30, 139. [Google Scholar] [CrossRef]
- Kowsari, S.; Deymi-Dashtebayaz, M. Energy, exergy and exergoeconomic (3E) analysis and multi-objective optimization of a closed-circuit desalination system with side-conduit. Desalination 2021, 514, 115154. [Google Scholar] [CrossRef]
- Alsadaie, S.; Mujtaba, I.M. Crystallization of calcium carbonate and magnesium hydroxide in the heat exchangers of once-through Multistage Flash (MSF-OT) desalination process. Comput. Chem. Eng. 2019, 122, 293–305. [Google Scholar] [CrossRef] [Green Version]
- Deymi-Dashtebayaz, M.; Dadpour, D.; Khadem, J. Using the potential of energy losses in gas pressure reduction stations for producing power and fresh water. Desalination 2021, 497, 114763. [Google Scholar] [CrossRef]
- Tayyeban, E.; Deymi-Dashtebayaz, M.; Dadpour, D. Multi objective optimization of MSF and MSF-TVC desalination systems with using the surplus low-pressure steam (an energy, exergy and economic analysis). Comput. Chem. Eng. 2022, 160, 107708. [Google Scholar] [CrossRef]
- Deymi-Dashtebayaz, M.; Nikitin, A.; Davoodi, V.; Nikitina, V.; Hekmatshoar, M.; Shein, V. A new multigenerational solar energy system integrated with near-zero energy building including energy storage–A dynamic energy, exergy, and economic-environmental analyses. Energy Convers. Manag. 2022, 261, 115653. [Google Scholar] [CrossRef]
- Ali, E. Understanding the operation of industrial MSF plants Part I: Stability and steady-state analysis. Desalination 2002, 143, 53–72. [Google Scholar] [CrossRef]
- Shariatpannahi, S.M.; Hatamipour, M.S.; Rashid-Nadimi, S.; Amini, M.K. Simultaneous saltwater desalination and power generation using an aluminum-powered cell. J. Environ. Chem. Eng. 2021, 9, 104802. [Google Scholar] [CrossRef]
- Deymi-Dashtebayaz, M.; Tayyeban, E. Multi objective optimization of using the surplus low pressure steam from natural gas refinery in the thermal desalination process. J. Clean. Prod. 2019, 238, 117945. [Google Scholar] [CrossRef]
- Darawsheh, I.; Islam, M.; Banat, F. Experimental characterization of a solar powered MSF desalination process performance. Therm. Sci. Eng. Prog. 2019, 10, 154–162. [Google Scholar] [CrossRef]
- Al-Weshahi, M.A.; Anderson, A.; Tian, G. Exergy efficiency enhancement of MSF desalination by heat recovery from hot distillate water stages. Appl. Therm. Eng. 2013, 53, 226–233. [Google Scholar] [CrossRef]
- Ali, M.B.; Kairouani, L. Multi-objective optimization of operating parameters of a MSF-BR desalination plant using solver optimization tool of Matlab software. Desalination 2016, 381, 71–83. [Google Scholar] [CrossRef]
- Al Ghamdi, A.; Mustafa, I. Exergy analysis of a MSF desalination plant in Yanbu, Saudi Arabia. Desalination 2016, 399, 148–158. [Google Scholar] [CrossRef]
- Sanaye, S.; Asgari, S. Four E analysis and multi-objective optimization of combined cycle power plants integrated with Multi-stage Flash (MSF) desalination unit. Desalination 2013, 320, 105–117. [Google Scholar] [CrossRef]
- Bandi, C.S.; Uppaluri, R.; Kumar, A. Global optimization of MSF seawater desalination processes. Desalination 2016, 394, 30–43. [Google Scholar] [CrossRef]
- Al-Hamahmy, M.; Fath, H.E.S.; Khanafer, K. Techno-economical simulation and study of a novel MSF desalination process. Desalination 2016, 386, 1–12. [Google Scholar] [CrossRef]
- Sharaf Eldean, M.A.; Soliman, A.M. A novel study of using oil refinery plants waste gases for thermal desalination and electric power generation: Energy, exergy & cost evaluations. Appl. Energy 2017, 195, 453–477. [Google Scholar] [CrossRef]
- Carrasquer, B.; Martínez-Gracia, A.; Uche, J. Exergy costs analysis of water desalination and purification techniques by transfer functions. Energy Convers. Manag. 2016, 126, 51–59. [Google Scholar] [CrossRef]
- Mabrouk, A.N.A. Technoeconomic analysis of once through long tube MSF process for high capacity desalination plants. Desalination 2013, 317, 84–94. [Google Scholar] [CrossRef]
- Al-Othman, A.; Tawalbeh, M.; El Haj Assad, M.; Alkayyali, T.; Eisa, A. Novel multi-stage flash (MSF) desalination plant driven by parabolic trough collectors and a solar pond: A simulation study in UAE. Desalination 2018, 443, 237–244. [Google Scholar] [CrossRef]
- Nafey, A.S.; Fath, H.E.S.; Mabrouk, A.A. Exergy and thermoeconomic evaluation of MSF process using a new visual package. Desalination 2006, 201, 224–240. [Google Scholar] [CrossRef]
- Hanshik, C.; Jeong, H.; Jeong, K.W.; Choi, S.H. Improved productivity of the MSF (multi-stage flashing) desalination plant by increasing the TBT (top brine temperature). Energy 2016, 107, 683–692. [Google Scholar] [CrossRef]
- Fiorini, P.; Sciubba, E. Thermoeconomic analysis of a MSF desalination plant. Desalination 2005, 182, 39–51. [Google Scholar] [CrossRef]
- Roy, Y.; Thiel, G.P.; Antar, M.A.; Lienhard, J.H. The effect of increased top brine temperature on the performance and design of OT-MSF using a case study. Desalination 2017, 412, 32–38. [Google Scholar] [CrossRef] [Green Version]
- Baig, H.; Antar, M.A.; Zubair, S.M. Performance characteristics of a once-through multi-stage flash distillation process. Desalin. Water Treat. 2010, 13, 174–185. [Google Scholar] [CrossRef]
- Khodadadi, F.; Deymi-Dashtebayaz, M.; Lakzian, E. Parametric analysis of combined power and freshwater producing system for natural gas engine heat recovery. Energy Convers. Manag. 2020, 225, 113464. [Google Scholar] [CrossRef]
- Amiri Rad, E.; Mohammadi, S.; Tayyeban, E. Simultaneous optimization of working fluid and boiler pressure in an organic Rankine cycle for different heat source temperatures. Energy 2020, 194, 116856. [Google Scholar] [CrossRef]
- Tayyeban, E.; Deymi-Dashtebayaz, M.; Gholizadeh, M. Investigation of a new heat recovery system for simultaneously producing power, cooling and distillate water. Energy 2021, 229, 120775. [Google Scholar] [CrossRef]
- Najafi, B.; Shirazi, A.; Aminyavari, M.; Rinaldi, F.; Taylor, R.A. Exergetic, economic and environmental analyses and multi-objective optimization of an SOFC-gas turbine hybrid cycle coupled with an MSF desalination system. Desalination 2014, 334, 46–59. [Google Scholar] [CrossRef]
- Dadpour, D.; Deymi-Dashtebayaz, M.; Hoseini-Modaghegh, A.; Abbaszadeh-Bajgiran, M.; Soltaniyan, S.; Tayyeban, E. Proposing a new method for waste heat recovery from the internal combustion engine for the double-effect direct-fired absorption chiller. Appl. Therm. Eng. 2022, 216, 119114. [Google Scholar] [CrossRef]
- Amiri Rad, E.; Mohammadi, S. Energetic and exergetic optimized Rankine cycle for waste heat recovery in a cement factory. Appl. Therm. Eng. 2018, 132, 410–422. [Google Scholar] [CrossRef]
- Kowsari, S.; Deymi-Dashtebayaz, M.; Karbasi, K.; Sheikhani, H. Optimal working conditions of various city gate stations for power and hydrogen production based on energy and eco-exergy analysis. Int. J. Hydrog. Energy 2020, 45, 22513–22533. [Google Scholar] [CrossRef]
- Hekmatshoar, M.; Deymi-Dashtebayaz, M.; Gholizadeh, M.; Dadpour, D.; Delpisheh, M. Thermoeconomic analysis and optimization of a geothermal-driven multi-generation system producing power, freshwater, and hydrogen. Energy 2022, 247, 123434. [Google Scholar] [CrossRef]










| Reference | Technology | Analysis | Capacity | Result |
|---|---|---|---|---|
| Nasser and Mabrouk [19] | MSF-BR and MSF-OT | Exergy and energy | 30.07 MIGD | Heat transfer area and pumping power of MSF-OT are lower than MSF-BR. |
| Al-Othman et al. [20] | MSF | - | 1880 m3/day | Two parabolic trough collectors can supply 76% of energy requirements. |
| Nafey et al. [21] | MSF-BR | Economic, exergy and energy | 18,000 m3/day | The unit product cost increases by 21% by decreasing the load down to 50% of the design point. |
| Hanshik et al. [22] | MSF-OT | Energy and exergy | - | The performance of MSF plants improves with increasing the top brine temperature. |
| Fiorini and Sciubba [23] | MSF | Exergy, energy and economic | 347.07 kg/s | The cogeneration MSF plant with a high top brine temperature and a low number of stages is preferred. |
| Yagnaseni Roy et al. [24] | MSF-OT | Energy balance | 3384 kg/s | The performance ratio increases by 41.5% with increasing the top brine temperature to 161 °C. |
| Hasan Baig et al. [25] | MSF | Energy balance | 378.8 kg/s | High temperature difference in the first stages and decreasing it in the last stages leads to a 3.13% decrease in condenser area and a 2.1% increase in performance ratio. |
| System Parameter | Value |
|---|---|
| Pump isentropic efficiency (%) | 70 |
| Brine heater efficiency (%) | 90 |
| Temperature of vapor in the first stage (°C) | 111.2 |
| Pressure of vapor in the first stage (kPa) | 200 |
| Feed water salinity (ppm) | 8935 |
| Freshwater salinity (ppm) | 0 |
| Ambient pressure (bar) | 1.01 |
| Ambient temperature (°C) | 25 |
| Equation | Balance Equation | Component |
|---|---|---|
| Heat Exchanger | Mass balance Energy balance | |
| Pump | Mass balance Energy balance | |
| Stage 1 | Mass balance Energy balance |
| Component | Capital Investment Cost |
|---|---|
| Brine Heater | |
| Pump | |
| Stage |
| Component | Exergoeconomic Equation | Auxiliary Equation |
|---|---|---|
| Brine Heater | ||
| Pump | ||
| Stage |
| Parameter | Current Study | Existing Data | Error |
|---|---|---|---|
| GOR | 6.405 | 6.5 | 1.46% |
| Inlet mass flow rate of feed brine | 371 (kg/s) | 356 (kg/s) | 4% |
| Mass flow rate of distillate water | 57 (kg/s) | 55.69 (kg/s) | 2.3% |
| Stage | ||||||
|---|---|---|---|---|---|---|
| 1 | 18.13 | 19.78 | 7.29 | 0.60 | 7.6 | 0.09 |
| 2 | 21.15 | 36.58 | 9.09 | 0.54 | 5.6 | 0.73 |
| 3 | 26.75 | 59.53 | 14.64 | 0.52 | 3.4 | 2.9 |
| 4 | 37.32 | 81.95 | 18.49 | 0.50 | 2.63 | 1.19 |
| 5 | 48.08 | 106 | 21.44 | 0.49 | 2.23 | 1.2 |
| 6 | 59.24 | 131.2 | 23.56 | 0.48 | 2 | 1.2 |
| 7 | 70.8 | 157.6 | 24.86 | 0.49 | 2 | 1.22 |
| 8 | 82.79 | 185.3 | 25.34 | 0.49 | 1.9 | 1.24 |
| 9 | 95.22 | 214.5 | 24.98 | 0.50 | 2 | 1.25 |
| 10 | 108.1 | 245.4 | 23.8 | 0.51 | 2.1 | 1.27 |
| 11 | 121.5 | 278.1 | 21.82 | 0.52 | 2.1 | 1.28 |
| 12 | 135.5 | 313 | 19.05 | 0.53 | 2.7 | 1.3 |
| 13 | 150.1 | 350.3 | 15.72 | 0.55 | 3.4 | 1.33 |
| 14 | 165.3 | 390.5 | 11.29 | 0.57 | 4.8 | 1.63 |
| 15 | 181.4 | 434.1 | 6.45 | 0.60 | 8.5 | 1.39 |
| 16 | 198.5 | 481.7 | 5.77 | 0.63 | 9.8 | 1.43 |
| 17 | 216.8 | 533.9 | 3.21 | 0.66 | 17.5 | 1.46 |
| 18 | 240.3 | 600.7 | 1.93 | 0.87 | 31.1 | 1.5 |
| Parameter | Value | Unit |
|---|---|---|
| Natural gas consumption | 34,272 | m3/year |
| CO2 emission production | 8 × 107 | kg/year |
| Natural gas cost | 9103 | $/year |
| Emission penalty cost | 193 × 104 | $/year |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farhadi, F.; Deymi-Dashtebayaz, M.; Tayyeban, E. Studying a Multi-Stage Flash Brine Recirculation (MSF-BR) System Based on Energy, Exergy and Exergoeconomic Analysis. Water 2022, 14, 3108. https://doi.org/10.3390/w14193108
Farhadi F, Deymi-Dashtebayaz M, Tayyeban E. Studying a Multi-Stage Flash Brine Recirculation (MSF-BR) System Based on Energy, Exergy and Exergoeconomic Analysis. Water. 2022; 14(19):3108. https://doi.org/10.3390/w14193108
Chicago/Turabian StyleFarhadi, Faezeh, Mahdi Deymi-Dashtebayaz, and Edris Tayyeban. 2022. "Studying a Multi-Stage Flash Brine Recirculation (MSF-BR) System Based on Energy, Exergy and Exergoeconomic Analysis" Water 14, no. 19: 3108. https://doi.org/10.3390/w14193108
APA StyleFarhadi, F., Deymi-Dashtebayaz, M., & Tayyeban, E. (2022). Studying a Multi-Stage Flash Brine Recirculation (MSF-BR) System Based on Energy, Exergy and Exergoeconomic Analysis. Water, 14(19), 3108. https://doi.org/10.3390/w14193108