A Reliability Analysis of a Rainfall Harvesting System in Southern Italy

Abstract

Rainwater harvesting (RWH) may be an effective alternative water supply solution in regions affected by water scarcity. It has recently become a particularly important option in arid and semi-arid areas (like Mediterranean basins), mostly because of its many benefits and affordable costs. This study provides an analysis of the reliability of using a rainwater harvesting system to supply water for toilet flushing and garden irrigation purposes, with reference to a single-family home in a residential area of Sicily (Southern Italy). A flushing water demand pattern was evaluated using water consumption data collected from a sample of residential customers during an extended measurement campaign. A daily water balance simulation of the rainwater storage tank was performed, and the yield-after-spillage algorithm was used to define the tank release rule. The model’s performance was evaluated using rainfall data from more than 100 different sites located throughout the Sicilian territory. This regional analysis provided annual reliability curves for the system as a function of mean annual precipitation, which have practical applications in this area of study. The uncertainty related to the regional model predictions was also assessed. A cost-benefit analysis highlighted that the implementation of a rainwater harvesting system in Sicily can provide environmental and economic advantages over traditional water supply methods. In particular, the regional analysis identified areas where the application of this system would be most effective.

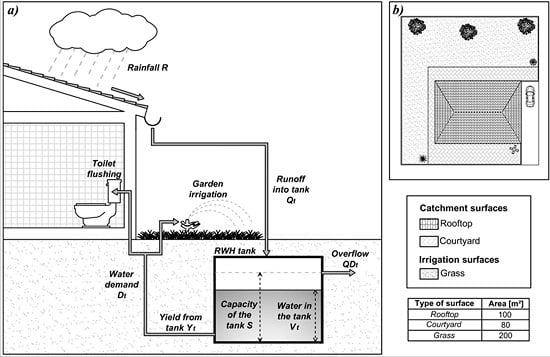
1. Introduction

Increasing water demand has led to water scarcity in many urban areas in the Mediterranean region. Indeed, population growth and the expansion of urban and industrialized areas has put great pressure on water resources. Climate change will intensify this pressure in some parts of the world, including the Mediterranean basin, Western United States and Southern Africa, resulting in a predicted decrease in water resources in the coming decades [1]. In this context, developing strategies and systems to identify alternative water resources will become critical, as will improving water resources management and planning. Water desalination and recycling processes, together with intermittent water supply, have long been the most common technologies used to cope with water scarcity in urban areas, while the benefits of collecting and using rainwater have largely been ignored [2,3]. Nevertheless, rainwater has historically been the primary source of water for potable and non-potable uses in locations where water supply systems have not yet been developed, and has traditionally been employed in a variety of ways in new settlements and isolated homes [4]. Because of their many environmental and economic advantages, rainwater harvesting (RWH) systems are currently receiving increased attention as alternative sources of drinking water, especially in semi-arid areas [5,6,7], but also in urban areas [8].

Generally, RWH systems involve three principal components: the catchment area, the collection device and the conveyance system. Rainwater is commonly collected from rooftops, courtyards or other compacted or treated surfaces before being filtered and collected in storage tanks to be used. RWH has many benefits. First, it requires simple and inexpensive technologies that are easy to install and maintain. Because of their simplicity, RWH systems can be expanded, reconfigured or relocated to meet each household’s needs. RWH also has important economic advantages for consumers because it reduces the amount of water purchased from public systems. Moreover, the possibility of having an alternative water supply reduces pressure on aquifers and surface water sources. For these reasons, the integration of RWH systems into buildings is an effective way to minimize the use of treated water for non-potable tasks and supply drinking water in places where water is scarce.

While RWH has numerous benefits, there are some disadvantages, particularly related to the limits of its supply and the reliability of rainfall (both in terms of spatial and temporal distribution). For these reasons, RWH systems cannot supply water for all domestic uses and are unlikely to make the households independent of the conventional water supply system. To achieve water self-sufficiency, multiple technologies must be employed. Nevertheless, the acquisition and use of rainwater through RWH can provide a considerable amount of water and ensure substantial financial savings to households.

The quantity and quality of collected rainwater depends on geographic location, local climate characteristics, the presence of anthropic activities in the area and storage tank volume. In general, rainwater is relatively clean, has low hardness and a quasi-neutral pH, and is free of sodium [9]. Runoff from rooftops is often considered unpolluted [10] or at least is of relatively good quality compared with runoff from surface catchments [11]. However, there is still disagreement about the quality of rooftop runoff, ranging from good or acceptable [12,13] to contaminated [14,15], depending on the roofing material, environmental conditions and atmospheric pollution. Subject to basic treatments such as filtration and/or chlorination, as necessary, collected rainwater can be utilized for different non-potable uses, including toilet flushing, washing machine use and garden irrigation (or any other use that does not require high-quality water). Different studies have highlighted the benefits of using harvested rainwater for toilet flushing [16,17]. Zhang et al. [18] observe that harvesting all roof runoff for use in toilet flushing can reduce water consumption in residential buildings by about 25%.

The performance and design of RWH systems has been investigated using different approaches, including water balance simulation analyses and mass curve analyses [19,20,21], probabilistic methods [22] and economic optimization [3]. The results indicate that the storage capacity of tanks cannot be standardized but is considerably influenced by local rainfall, catchment surface characteristics and the number of people in the household.

Several studies have explored the implementation of RWH systems in response to growing water demand in Africa [7,23,24], Asia [25,26,27], USA. [17,18,19,20,21,22,23,24,25,26,27,28] and Australia [18,19,20,21,22,23,24,25,26,27,28,29]. Additional studies on RWH systems have been carried out in the Mediterranean region as well. In Greece, Sazakli et al. [30] analyzed the quality and utilization of rainwater for domestic and drinking purposes. In Spain, Farreny et al. [8] analyzed the cost-efficiency of an RWH system in a high-density social housing neighbourhood comprised of multi-storey buildings. In Southern Italy, Campisano and Modica [31] defined a dimensionless methodology to derive the optimal design of RWH systems for domestic use. This methodology was based on the results of daily water balance simulations carried out for 17 rainfall gauging stations.

The present study investigated the performance of a proposed RWH tank for a model single-family home in a residential area. Performance was tested for varying levels of annual precipitation using data from over 100 different sites in Sicily. The application of the yield-after-spillage algorithm enabled an evaluation of site-specific system efficiency. Performance was assessed for three tank sizes (10, 15 and 20 m³) and three uses of the collected rainwater: toilet flushing, garden irrigation and both uses combined. Simulations were run using data from 2002 to 2004. The researchers analyzed water consumption data recorded from single-family homes in Palermo (Northwestern Sicily) during the selected time period to define a temporal pattern for flushing water demand. Water demand for garden irrigation was defined using recorded mean monthly evapotranspiration rates. Once the system’s performance was evaluated for the entire study area, its reliability was analyzed as a function of mean annual precipitation to determine mathematical expressions that have regional validity and could be practically applied. A data resampling procedure was applied to evaluate uncertainty related to the regional model previsions. Finally, a cost-benefit analysis was performed in order to estimate the payback period on the capital cost for the RWH system installation.

The study highlights the limits and benefits related to the application of RWH systems in the area of study. In particular, the regional analysis allowed researchers to identify areas in which the installation of the selected RWH system would be most effective and for which rainwater uses.

2. Materials and Methods

2.1. Dataset

The present analysis uses data from Sicily, one of the 20 administrative regions in Italy, as a case study for a selected rainwater harvesting system. Sicily is an island of approximately 25,700 km² located in Southern Italy and is characterized by a Mediterranean climate (mild winters and hot, generally dry summers). The total annual rainfall in this area ranges from 400 mm/year at lower elevations to 1300 mm/year at higher elevations. Figure 1 shows the spatial distribution of mean annual precipitation over the 1981–2012 period in Sicily.

Figure 1. Spatial distribution of mean annual rainfall for the 1981–2012 period and locations of rain gauges.

Figure 1. Spatial distribution of mean annual rainfall for the 1981–2012 period and locations of rain gauges.

Figure 2 illustrates the RWH system analyzed and provides a diagram of the different surface materials and their areas (m²) onsite. The water catchment surfaces of the model home include the home’s rooftop and the courtyard, for a total catchment area of 180 m² (100 m² of rooftop and 80 m² of courtyard and pedestrian areas). In this simulation, rainfall is collected from these surfaces and stored in a rainwater tank for two non-potable uses: toilet flushing and garden irrigation.

Figure 2. (a) Scheme of the RWH system; and (b) layout of the single-family house with the representation of the different surfaces.

Figure 2. (a) Scheme of the RWH system; and (b) layout of the single-family house with the representation of the different surfaces.

The implementation of an RWH system requires an evaluation of the water balance, for which rainfall represents inflow and water demand for toilet flushing or for garden irrigation is the outflow. In the present study, rainfall volumes were calculated using the daily rainfall series recorded from 111 rain gauges over the 2002–2004 period (Figure 1). Rainfall data were provided by the Osservatorio delle Acque-Agenzia Regionale per i Rifiuti e le Acque (OA-ARRA) of Sicily. This period was chosen because a large number of the evenly distributed rain gauges that monitor rainfall throughout the Sicilian territory worked continuously during the entire period. This historical rainfall series is representative of the regional climate both in terms of annual and monthly mean values.

Water demand for flushing was calculated as the number of daily flushes per capita, which was obtained by analyzing water consumption data collected at a high temporal resolution from four-person single-family homes in Palermo (Northwestern Sicily) during a two-year measurement campaign. Water demand for garden irrigation was evaluated by estimating the mean monthly reference evapotranspiration. Historical temperature data obtained from the OA-ARRA for the 1981–2012 period were used for this calculation.

2.2. Inflow to the RWH Tank

The modelled rainwater tank is filled exclusively using rainfall volumes from a building’s rooftop, courtyard and pedestrian areas. Assuming constant rainfall within each time step t, the rainwater volume can be calculated as follows:

$$Q_t=\mathsf{\varphi }\cdot A_{TOT}\cdot R_t=A\cdot R_t$$

(1)

where Q_t is the inflow volume supplied to the tank at time step t (m³), φ is the runoff coefficient depending on water loss (dimensionless), R_t is the rainfall at time t (m), A_TOT is the total catchment surface area (m²), and A is the effective impervious surface area (m²). Evaporation losses from the tank are neglected. In this study, φ was set equal to 0.9 [32].

The stormwater quality of the initial discharge from the roof surface was of poor quality due to an accumulation of dust, sediments, bird and animal droppings, and leaves and debris from the surrounding areas [33], all of which were accumulated during the dry periods and washed off at the beginning of the next rain. The first flush is defined as the initial period of a rainwater runoff where a pollutant concentration is considerably higher than during later periods [34]. Depending on the specific site characteristics, type of contaminant and final use of the water, the literature provides different values of the amount of water that has to be diverted to ensure an adequate water quality. Yaziz et al. [35] and Coombes [36] reported that subtracting the first 0.33 mm of rainfall from the total daily rainfall as the first flush would significantly improve roof water quality. Following this recommendation, all the daily water balance simulations have been performed subtracting the first flush of 0.33 mm from the daily rainfall series.

2.3. Water Demand for Toilet Flushing

Estimating the average number of daily flushes per capita could be considered satisfactory to accurately model daily water demand for toilet flushing; however, these observations may not be universally applicable to all rainwater collection systems. Therefore, demand patterns with significant daily variations may require more precise modeling.

The water balance at the rainwater tank in the present study was evaluated at daily scale. The toilet flushing demand pattern was determined by analyzing water consumption data collected during a monitoring campaign of seven dwellings located in Palermo (Northwestern Sicily) throughout 2002–2004 (Figure 3).

Figure 3. (a) Water demand percentiles of recorded data for Dwelling 6; and (b) Weibull cumulative distribution function CDF fitting the cumulated frequency of the number of daily flushing per capita for Dwelling 6.

Figure 3. (a) Water demand percentiles of recorded data for Dwelling 6; and (b) Weibull cumulative distribution function CDF fitting the cumulated frequency of the number of daily flushing per capita for Dwelling 6.

The customers that participated in the consumption monitoring program had the following characteristics: families with at least two members; family members ranging in age from 4 to 70 years; negligible outdoor consumption; and interest in participating. Each monitored dwelling had a toilet WC flush tank with a volume of 9–10 L (the usual volume for a WC flush tank in Italy) and a bowl filling time ranging between 0.95 and 1 min.

An instrument package, including a Class C multi-jet water meter and a data logger, was installed on the service line of each of the seven dwellings downstream of the revenue water meter to monitor domestic water use. The two devices were coupled by means of an impulse sensor. When cumulative volume consumed equaled 0.5 L, the sensor transmitted a signal to the data logger. A common faucet is characterized by flows in the range 6–12 L/min, and the meter was able to disclose consumption pulses longer than or equal to 5 s (in the worst case) or equal to 2.5 s (in the best case), allowing researchers to separate out toilet flushing data from other uses. In any case, if small pulses were not identifiable, their volume was aggregated into the next consumption pulse. Cumulative volumes of more than 0.5 L were recorded in a text file containing six fields (i.e., day, month, year, hour, minute and second). Water demand data were collected periodically by connecting the data logger to a laptop. The monitoring period was approximately one year for five dwellings, less than one year for two dwellings, and more than two years for one dwelling (Table 1). The monitoring period was long enough to identify weekly, monthly and seasonal toilet flushing patterns and was clear enough to identify user presence at home.

Once the data were acquired, according to the procedure proposed by Campisano and Modica [31], as first step of the analysis, the number of daily flushing was evaluated for each dwelling and monitoring day. To this purpose, the water consumption data were filtered to identify data points where use ranged from 9 to 10 L over a period of one minute. Knowing the filling time of the WC flush tank was important to exclude consumption data with the same volume but linked to other uses. In the absence of more specific information, the number of daily flushes per capita was then calculated for all monitored days as the number of flushes per day divided by the average number of users present, or the number of family members in each monitored household.

Table 1. Results of statistical analysis carried out on water consumption data collected for seven dwellings located in Palermo and monitored throughout 2002–2004.

Dwelling	n° Persons	Monitoring Days	Average Flushings/(Day·Capita)	RMSE	CDF	λ	κ	K-S Test D0.05
1	3	334	5.73	2.925	Weibull	6.66	2.234	0.071
2	4	359	5.77	2.951	Weibull	6.57	2.094	0.068
3	2	317	4.79	2.978	Weibull	5.77	1.912	0.060
4	3	237	4.62	2.974	Weibull	5.34	1.654	0.065
5	2	212	6.46	2.883	Weibull	7.31	2.410	0.077
6	4	637	5.12	2.798	Weibull	5.90	2.020	0.022
7	3	320	4.75	2.980	Weibull	5.35	1.674	0.059

Table 1. Results of statistical analysis carried out on water consumption data collected for seven dwellings located in Palermo and monitored throughout 2002–2004.

Dwelling	n° Persons	Monitoring Days	Average Flushings/(Day·Capita)	RMSE	CDF	λ	κ	K-S Test D0.05
1	3	334	5.73	2.925	Weibull	6.66	2.234	0.071
2	4	359	5.77	2.951	Weibull	6.57	2.094	0.068
3	2	317	4.79	2.978	Weibull	5.77	1.912	0.060
4	3	237	4.62	2.974	Weibull	5.34	1.654	0.065
5	2	212	6.46	2.883	Weibull	7.31	2.410	0.077
6	4	637	5.12	2.798	Weibull	5.90	2.020	0.022
7	3	320	4.75	2.980	Weibull	5.35	1.674	0.059

The average number of daily flushes per capita for each monitored dwelling is reported in Table 1, along with the associated Root Mean Square Error (RMSE). These values ranged from 4.62 (Dwelling 4) to 6.46 (Dwelling 5) daily flushes per capita. The related RMSE was approximately 2.9 for five dwellings, 2.883 for one dwelling, and 2.798 for the final dwelling. These results are similar to those reported in previous studies available in the literature [31,32,33,34,35,36,37]. The number of daily flushes per capita were then statistically analyzed to identify a well-fitting probability distribution function. Several probability distribution functions were investigated, including the Normal, Poisson, Weibull, Exponential, etc. All monitored dwellings revealed similar statistical behaviors; the Weibull distribution function fit the observed data best. This was confirmed using the Kolmogorov-Smirnov statistical test (confidence level equal to 0.05). Table 1 also reports data for the two parameters λ and κ of the related Weibull distribution function together with the results of the Kolmogorov-Smirnov test for each dwelling.

An analysis of the processed data revealed that Dwelling 6 was representative of all monitored dwellings, with an average number of flushes per capita per day equal to 5.12 and a minor RMSE value equal to 2.798. Moreover, this household was continuously monitored for the longest period of time (around two years). Therefore, the subsequent RWH analysis uses Dwelling 6 to define the water demand pattern for toilet flushing in Sicily. Figure 3a shows the percentiles (25th, 50th and 95th) of the water demand data collected for Dwelling 6 during the monitoring campaign. Figure 3b shows the Weibull cumulative distribution function CDF fitting the cumulated frequency of the obtained per capita flushes for Dwelling 6.

To generalize the results to other similar users, 365 random points were sampled from this CDF to construct a daily pattern for an entire year of toilet flushes per capita. Finally, the series of daily household toilet flushes was computed by multiplying the number of flushes derived in the previous step by a selected number of users at home during the day.

2.4. Water Demand for Garden Irrigation

The frequency of irrigation depends on the type of grass, soil properties, and climatic conditions at the examined site. To evaluate the water demand for garden irrigation, it was assumed that the garden area (200 m²) of the modelled single-family house was planted with turfgrass. To evaluate water demand, the mean monthly reference evapotranspiration ET₀ value was calculated for the area of study using the Thornthwaite formula [38]. ET₀ approximates water use for an irrigated grass pasture; therefore, water use for turfgrasses was estimated using a correlation factor, the crop coefficient K_c, as follows:

$$ET=E{T}_0\cdot K_c$$

(2)

where ET is the actual evapotranspiration in mm/day. Turfgrass K_c values fluctuate slightly during the season based on the percentage of plant cover, growth rate, root growth, stage of plant development and management practices. In this study, K_c was set equal to 0.85 [39].

Once the amount of water to be provided was determined, the frequency of irrigation was defined based on practical considerations and previous literature. Optimum irrigation frequency depends on site, plant species, climatic conditions and soil types. Some studies (e.g., [40,41]) have highlighted that deep and infrequent irrigation promotes plant tolerance to drought stress. In a hot, humid region of the US, Jordan et al. [42] showed that irrigating every 4 days produced a larger and deeper root system. Moreover, irrigation scheduling is a process that requires knowledge of the irrigation system’s characteristics, such as application rate and distribution uniformity. Watering frequency will vary from site to site and should be determined by the appearance of the turf. During peak water demand, turfgrass irrigation should occur every two or three days depending on the soil texture and root depth. For extremely arid climates, and depending on the type of turfgrass, the irrigation interval should be daily; but, during the early spring and in fall and winter, the frequency or irrigation interval may be stretched to every five to seven days [43]. Marchione [44] investigated the effects of different irrigation regimes on turfgrasses in Southern Italy and showed that, in a Mediterranean climate characterized by low rainfall and high evapotranspiration rates during summer, irrigation regimes equal to 75% of the water deficit are not adequate to maintain an acceptable turf quality.

The need for additional information to define the optimal irrigation frequency for turfgrass required to make some assumptions in this study. Specifically, it was assumed that the garden was planted with a turfgrass more resistant to warm climates than other species, such as Zoysia Japonica Compadre. It was also assumed that the garden was only irrigated every 3 days during April, May and September, and on alternate days from June to August. Table 2 summarizes the potential and actual daily evapotranspiration and the irrigation frequency for each month the garden was irrigated with harvested rainwater.

Table 2. Potential and actual evapotranspiration (mm/day) and the irrigation frequency for each month of garden irrigation with harvested rainwater.

Month	Evapotranspiration (mm/day)		Irrigation Frequency
	Reference	Actual
April	1.5	1.3	every 3 days
May	2.4	2.0	every 3 days
June	3.5	3.0	alternate days
July	4.3	3.7	alternate days
August	4.5	3.8	alternate days
September	3.5	3.0	every 3 days

Table 2. Potential and actual evapotranspiration (mm/day) and the irrigation frequency for each month of garden irrigation with harvested rainwater.

Month	Evapotranspiration (mm/day)		Irrigation Frequency
	Reference	Actual
April	1.5	1.3	every 3 days
May	2.4	2.0	every 3 days
June	3.5	3.0	alternate days
July	4.3	3.7	alternate days
August	4.5	3.8	alternate days
September	3.5	3.0	every 3 days

2.5. Water Balance Simulation

Different models can be used to predict the performance of RWH systems [45,46]. Often simple mass balance approaches based on annual precipitation volumes are used. However, these procedures do not ensure a proper level of accuracy in sizing RWH systems. Behavioural models are also frequently applied because they allow a more detailed design and are relatively simple to develop, although Ward et al. [46] showed that they usually underestimate the need for storage tank capacity compared with simple mass balance simulations.

In a behavioral model, the changes in the storage content of a finite reservoir are computed using the water balance equation. In this model, water fluxes consist of runoff into a tank (inflow), overflow from the tank and the yield extracted from the tank; demand is met in each operating period to the extent that storage is available.

The algorithm for the model relies on a yield-after-spillage (YAS) operating rule [47]:

$$Q_{D_t}=\max \{\begin{array}{l}{V}_{t-1}+A\cdot R_t-S\\ 0\end{array}$$

(3)

$$Y_t=\min \{\begin{array}{l}{D}_t\\ V_{t-1}\end{array}$$

(4)

$$V_t=\min \{\begin{array}{l}{V}_{t-1}+A\cdot R_t-Y_t\\ S-Y_t\end{array}$$

(5)

where, Q_Dt (m³) is the volume discharged as overflow from the storage tank at time step t, V_t (m³) is the volume stored at time step t, Y_t (m³) is the yield of rainwater from the storage tank at time step t, D_t (m³) is the toilet and grass irrigation water demand at time step t, and S (m³) is the tank storage capacity.

The performance of RWH systems is generally described in terms of volumetric reliability, expressed as the total actual rainwater supply over water demand, R_v:

$$R_V=\frac{{\displaystyle \sum _{t=1}^T{Y}_t}}{{\displaystyle \sum _{t=1}^T{D}_t}}\cdot 100$$

(6)

where T is the total time period under consideration and R_t is the overall water savings that can be achieved by harvesting and using rainwater. Equation (6) provides a measure of how much water has been conserved in comparison to the overall demand, and is also referred to as water saving efficiency [45].

3. Results and Discussion

3.1. Evaluation of Daily Reliability

The historical rainfall series recorded at 111 rain gauges during the 2002–2004 period were used to evaluate the performance of the RWH system in Figure 2. First of all, a preliminary analysis was carried out in order to examine the effect of the tank capacity S on the daily reliability R_V and to identify the tank capacity providing the most feasible value of the average daily R_V for each site in Sicily (assuming the same system configuration in terms of catchment surface).

Several tank capacities S in the range 1–30 m³ were considered. Water balance simulations were performed at daily scale, thus accounting for the effect of extreme rainfall of 24 h duration and dry spells on the RWH system. Namely, for any tank size, the daily average R_V of each site was computed on the entire analysis period. Then, the related percentiles values were estimated. Results are summarized in the box-whisker graphs in Figure 4.

Focusing on the median line (50th percentile), the average daily R_V grows with tank capacity: For S ranging between 1 and 30 m³, R_V varies in the range from 43% to 94% for toilet flushing use; this rise is steeper for irrigation use, specifically from 31% to 95%, while it is moderate for the combined use (R_V ranging from 39% to 80%).

Regarding toilet flushing use, when S is equal to 10 m³, the RWH system reliability is higher than 80% and is equal to 92% for a capacity of 20 m³. Further increases of S produce a slight improvement of R_V, with an achievable maximum value equal to 94%. For irrigation use, the median line shows an higher dependence of R_V on S. The system is able to provide an R_V value equal to 95% in more than 50% of the analyzed sites when a capacity of 30 m³ is accounted. For this use the temporal shift between the rainwater demand for irrigation (higher during summer months) and rainfall amounts (lower during summer months) highly affects RWH system performance: Higher tank capacities permit the storing of greater rainwater volumes in winter in order to satisfy irrigation demand in summer. This effect is mitigated if combined use is considered because, in this case, the rainwater demand is widespread throughout the entire year. Indeed, the average daily R_V slightly increases for capacities higher than 10 m³.

Figure 4. Box-whisker graphs of the daily reliability R_V vs. tank capacity S for different rainwater uses. (a) toilet flushing use; (b) irrigation use; (c) toilet flushing and irrigation use.

Figure 4. Box-whisker graphs of the daily reliability R_V vs. tank capacity S for different rainwater uses. (a) toilet flushing use; (b) irrigation use; (c) toilet flushing and irrigation use.

In order to assess the uncertainty linked to the R_V appraisal for each site, the average width of the R_V percentiles band (shown in Figure 4) was computed. Regarding the 25th and 75th percentile band, the average width values are equal to 19.8%, 8.8% and 7.1% for toilet flushing, irrigation and combined use, respectively. The average uncertainty regarding the 5th and 95th percentile band is 19.2% for combined use and about 24.5% for toilet flushing and irrigation. The reduced variability of R_V values among the analyzed sites for combined use highlights that rainwater demand represents a limiting factor to the achievement of higher RWH system performance in all the analyzed sites.

The performance improvement of RWH system in terms of R_V is moderate and not advantageous for tank capacity greater than 20 m³ for toilet flushing and combined uses. Tank capacities higher than 20 m³ may provide a significant improvement for irrigation use, but could be less economically feasible for a residential household (see Section 3.5. Cost-benefit analysis). Therefore, after this preliminary analysis, the performance of the RWH system were investigated focusing on three different capacities: 10, 15 and 20 m³.

In order to analyze the effect of the temporal aggregation of the daily water balance output on R_V , the system performance was evaluated, for each site, at annual and monthly scales according to Equation (6). The following sections illustrate the obtained results.

3.2. Analysis of Annual Reliability

The annual reliability of the RWH system for each site of the studied area was assessed as average of the annual R_V values related to the three years chosen as the analysis period.

Figure 5 shows the spatial distribution of the annual reliability values over the study area. The use of the RWH system for toilet flushing provided the highest mean annual R_V values. The amount of water needed for toilet flushing for a family of four is approximately 80 m³ per year. In the northwestern part of the island, where the mean annual precipitation ranges from 600 to 1000 mm, the performance of the system reached R_V values close to 100%, meaning that, in this area, the demand of water for toilet flushing can be completely satisfied by the water stored in an RWH system with a tank volume of just 10 m³. Reliability was lower in sites located along the Mediterranean coast, where the mean annual precipitation ranges from 400 to 600 mm. In this zone, a 20 m³ storage capacity was able to ensure reliability values up to 80%. A 10 m³ RWH tank appears sufficient to ensure adequate R_V values in most of the area of study, while a larger capacity is required in the driest areas of the island. Conversely, a 10 m³ storage capacity is not enough to meet the water demand for garden irrigation. Figure 5 shows that the use of an RWH system for garden irrigation results in poor performance. Specifically, for S = 10 m³, the mean annual R_V was approximately 55%.

Figure 5. Spatial distribution of mean annual reliability R_V (%) for different rainwater uses and for S equal to 10, 15 and 20 m³.

Figure 5. Spatial distribution of mean annual reliability R_V (%) for different rainwater uses and for S equal to 10, 15 and 20 m³.

A wide area along the southern coast had R_V values that ranged from 35% to 45%. Therefore, a 10 m³ storage capacity is not able to meet half of the annual water demand for garden irrigation. For this use, a 15 m³ storage capacity increased reliability just 5% (R_V ranging from 45% to 50%). The use of a 20 m³ tank was able to ensure good performance only in the northern part of the island, where the annual reliability of the system reached 80%; in the South, R_V ranged between 60% and 70%. To completely meet the water demand for garden irrigation, higher volumes of harvested rainwater are required. The mean annual demand for irrigation water is approximately 45 m³; however, unlike the water demand for toilet flushing, which is homogeneously distributed over the year, irrigation demand is concentrated in spring and summer and has a peak in August. This temporal pattern deeply affects the performance of RWH systems because rainfall is scarce in Sicily during summer months, when increased evapotranspiration rates result in greater water demands for irrigation.

In the combined use case, the tank volumes considered in this analysis were not sufficient to ensure adequate system performances. The maps show that, when S is equal to 10 m³, the average R_V was approximately 50%. Increased storage capacity up to 20 m³ provided a slight increase in reliability, mainly in the northeastern part of the island, where the mean annual precipitation reaches 1,000 mm. Therefore, when limited rooftop and courtyard areas are available, the increase in storage volume is not enough to ensure the good performance of the RWH system, especially when rainwater must fill multiple needs with different temporal demand patterns, such as toilet flushing and garden irrigation. Furthermore, the increase in costs related to the installation of a larger storage tank makes the use of an RWH system less advantageous as capacity requirements increase.

3.3. Analysis of Monthly Reliability

To analyze the monthly variability of the RWH system’s reliability, a separate analysis was performed for a particular location. The site selected for this analysis was Palermo, located on the northwestern coast of the island, where consumption data for toilet flushing were measured and analyzed. For S = 20 m³, Figure 6a,d,g show plots of mean monthly demand, rainfall volumes and yield over the simulation period, as well as the corresponding monthly variation in reliability R_V when rainwater is used to flush toilets.

Figure 6. Monthly water demand, rainfall volume and yield, and monthly variation of system reliability for toilet flushing (a,d,g); garden irrigation (b,e,h); and both uses (c,f,i).

Figure 6. Monthly water demand, rainfall volume and yield, and monthly variation of system reliability for toilet flushing (a,d,g); garden irrigation (b,e,h); and both uses (c,f,i).

In Figure 6a, water demand and rainfall volumes are compared. Water demand for toilet flushing is clearly unaffected by monthly and seasonal variations, and shows only slight differences from month to month (on the order of 1 m³), while rainfall volumes are affected by an evident seasonal pattern, with the lowest values occurring during summer months and the minimum value occurring in July. Figure 6d shows water demand and yield. When demand and yield overlap or the yield exceed the demand, the RWH system is able to completely meet the water demand for toilet flushing, ensuring a reliability of 100% (Figure 6g). Monthly R_V varies between 74% (in August) and 100% (in May, June, October, November and December).

In the case of garden irrigation (Figure 6b,e,h), the RWH system must provide water only during the period from April to September. Water demand is highest during summer months (Figure 5b), when temperatures are higher and evapotranspiration increases. Figure 6e shows that the demand exceeds the yield in June, July, August and September. This accounts for low monthly R_V values, especially in August when R_V equals 20% (Figure 6h), and means that a significant volume of water would need to be collected from other sources when rainwater is unavailable from the tank. For the examined site and the considered system, the use of rainwater for garden irrigation appears disadvantageous during summer months because the RWH system is not able to provide high levels of water savings compared to the costs incurred for system installation and maintenance. Because the water demand volumes are higher than the maximum capacity of the tank (20 m³), the poor performance of the system highlights the need to accumulate more rainwater during rainfall events by increasing the area of collection surfaces.

Figure 6c,f,i shows the results of the RWH system under the combined use scenario. The total water demand is the sum of monthly water volume required for toilet flushing and monthly water volume needed for garden irrigation (Figure 6c). The demand for irrigation is much higher than that for toilet flushing, as shown by the consistent increase in total water demand during the summer months. However, the water collected during the winter, spring and autumn months ensures adequate yields to meet the water demand for toilet flushing, reaching R_V levels up to 100% (Figure 6f). The performance of the RWH system clearly declines during the summer when the collected water is not enough to meet the higher demand for garden irrigation, resulting in a significant decrease in monthly R_V (Figure 6i).

3.4. Regional Reliability Curves and Related Uncertainty

The relationship between annual reliability and mean annual precipitation was investigated to define equations for a system analogous to the one analyzed here (for S equal to 10, 15 and 20 m³) and valid at the regional scale. The goal of these equations is to provide a reliability R_V that an RWH system can attain at an annual scale for each value of mean annual precipitation P and the uncertainty related to its estimation. Starting from simulation results previously shown, the points (P, R_V) were interpolated according to the following procedure:

• From the original dataset of annual reliabilities of the RWH system, which were obtained by applying the YAS algorithm to the 111 sites distributed over the Sicilian territory for the 2002–2004 period, 10,000 sub-datasets were extracted, in which 30% of points were randomly excluded to investigate the uncertainty affecting the results related to the selected sites;
• for each sub-dataset the interpolation curve was estimated;
• for each value of P, the 5th, 50th and 95th percentiles were obtained from the interpolation curves. The interpolation curve obtained for the 50th percentile represents the relationship between P and R_V, while the uncertainty related to the estimation of R_V as a function of P is given by the width of the interpolation curves for the 5th and 95th percentiles, respectively.

For each rainwater use and each value of S, Figure 7 shows the interpolation curves and the resulting uncertainty bands (dotted lines) obtained by interpolating the 5th and 95th percentiles. Table 3 shows the equation of the curves and the uncertainty bands. In general, reliability increases with mean annual precipitation and tank size. For the same values of P, the highest reliability can be obtained using the harvested rainwater only for toilet flushing. In this case, the RWH system is able to ensure an annual R_V that varies from 80% and 100% in locations characterized by a mean annual precipitation ranging from 600 to 1000 mm. According to these results, the installation of an RWH tank is particularly effective on the northeastern part of the island (as shown in Figure 5).

In terms of rainwater use for garden irrigation, when S = 10 m³ R_V does not reach 100% even at the sites with the highest mean annual precipitation values. Garden irrigation requires a storage of at least 20 m³ to obtain higher values of R_V; however, these values remain under 100%. The curves illustrate that the RWH system’s performance declines if the rainwater is intended for the dual uses of toilet flushing and garden irrigation.

For every use, the evaluation of the system’s reliability is affected by a lower level of uncertainty corresponding to a mean annual precipitation in the range from 600 to 1000 mm, as shown by the smaller width of the band. R_V values that exceed 100% indicate that the installation of an RWH system can completely meet the water demand and supply additional volume, which could be allocated to other uses. This occurs where the mean annual precipitation is greater than 1400, 1200 and 1100 mm when S equals 10, 15 and 20 m³, respectively. However, the uncertainty related to higher values of P is greater than that related to the range 600–1000 mm, as shown by the increased width of the band of uncertainty.

Table 3. Equations of interpolating curves of 5th, 50th and 95th percentiles for each rainwater use and tank volume.

Rainwater Use	Tank Volume(m3)	P-RV Curve	Uncertainty Bands
		50th Percentile	5th Percentile	95th Percentile
toilet flushing	10	0.0276 × P + 61.782	−7 × 10−6 × P2 + 0.0379 × P + 56.864	8×10−6 × P2 + 0.0148 × P + 68.685
	15	0.0299 × P + 64.589	−8×10−6 × P2 + 0.0445 × P + 57.073	8×10−6 × P2 + 0.0191 × P + 69.642
	20	0.0316 × P + 66.804	−1×10−5 × P2 + 0.0505 × P + 57.233	1×10−5 × P2 + 0.0164 × P + 74.115
garden irrigation	10	0.0183 × P + 41.614	−6×10−6 × P2 + 0.0271 × P + 36.728	6×10−6 × P2 + 0.0104 × P + 46.063
	15	0.0200 × P + 51.705	−9×10−6 × P2 + 0.0352 × P + 43.927	8×10−6 × P2 + 0.0087 × P + 57.493
	20	0.0214 × P + 61.223	−8×10−6 × P2 + 0.0338 × P + 54.87	7×10−6 × P2 + 0.0113 × P + 66.569
toilet flushing and garden irrigation	10	0.0233 × P + 38.775	−7×10−6 × P2 + 0.0335 × P + 33.891	8×10−6 × P2 + 0.0125 × P + 44.048
	15	0.0282 × P + 38.482	−9×10−6 × P2 + 0.0424 × P + 31.477	9×10−6 × P2 + 0.0153 × P + 44.332
	20	0.0320 × P + 38.508	−9×10−6 × P2 + 0.0466 × P + 31.437	9×10−6 × P2 + 0.0185 × P + 45.036

Table 3. Equations of interpolating curves of 5th, 50th and 95th percentiles for each rainwater use and tank volume.

Rainwater Use	Tank Volume(m3)	P-RV Curve	Uncertainty Bands
		50th Percentile	5th Percentile	95th Percentile
toilet flushing	10	0.0276 × P + 61.782	−7 × 10−6 × P2 + 0.0379 × P + 56.864	8×10−6 × P2 + 0.0148 × P + 68.685
	15	0.0299 × P + 64.589	−8×10−6 × P2 + 0.0445 × P + 57.073	8×10−6 × P2 + 0.0191 × P + 69.642
	20	0.0316 × P + 66.804	−1×10−5 × P2 + 0.0505 × P + 57.233	1×10−5 × P2 + 0.0164 × P + 74.115
garden irrigation	10	0.0183 × P + 41.614	−6×10−6 × P2 + 0.0271 × P + 36.728	6×10−6 × P2 + 0.0104 × P + 46.063
	15	0.0200 × P + 51.705	−9×10−6 × P2 + 0.0352 × P + 43.927	8×10−6 × P2 + 0.0087 × P + 57.493
	20	0.0214 × P + 61.223	−8×10−6 × P2 + 0.0338 × P + 54.87	7×10−6 × P2 + 0.0113 × P + 66.569
toilet flushing and garden irrigation	10	0.0233 × P + 38.775	−7×10−6 × P2 + 0.0335 × P + 33.891	8×10−6 × P2 + 0.0125 × P + 44.048
	15	0.0282 × P + 38.482	−9×10−6 × P2 + 0.0424 × P + 31.477	9×10−6 × P2 + 0.0153 × P + 44.332
	20	0.0320 × P + 38.508	−9×10−6 × P2 + 0.0466 × P + 31.437	9×10−6 × P2 + 0.0185 × P + 45.036

Figure 7. Reliability curves and their uncertainty bands for each uses and analyzed storage volumes.

Figure 7. Reliability curves and their uncertainty bands for each uses and analyzed storage volumes.

In every case, the width of the uncertainty bands increases for the lowest and highest values of mean annual precipitation. In the case of the lowest values, the uncertainty is related to the fact that the reliability of the system is considerably affected by the amount of harvested rainwater, because of the potential failure of the RWH system in meeting the water demand. In the case of the highest values, the uncertainty in the reliability is related to the fact that the amount of harvested water is likely to exceed the water demand. The installation of an RWH system in the above mentioned cases requires a deeper analysis to verify its cost-effectiveness. Where the amount of rainwater is not enough to meet the water demand, the analyzed volumes and collection surfaces are not adequate to ensure a high level of water savings, making households dependent on other water sources for most or part of the year. On the other hand, where the amount of rainwater exceeds the needs of the household, the rainwater that overflows the storage tank represents an economic loss because this water could meet other demands, allowing a greater independence from the traditional supply system and, therefore, further savings.

3.5. Cost-Benefit Analysis

An economic analysis of the RWH system was carried out in order to investigate the balance between the investment/cost for system purchase and installation, and the benefits obtained by the rainwater use for the three considered demands. To this aim, a schematic underground installation of an RWH system was considered, consisting of a pre-fabricated concrete tank provided with a first flush device, a manhole with a rainwater filter, a pumping system and its Programmable Logic Controller (PLC) equipment, the drainage piping system inlet and outlet, the tank, and the piping distribution system to supply the rainwater for the analyzed uses (Figure 8). Table 4 summarizes the costs of the RWH system elements for each tank capacity and each use. These costs have been obtained starting from the unit rates, drawn from the official regional price list for civil infrastructures [48], and by means of a market survey.

Figure 8. Schematic underground installation of the RWH system.

Figure 8. Schematic underground installation of the RWH system.

The tank purchase and installation highly affects the total RWH system cost (Table 4), as confirmed by different studies in the literature [49,50,51]. Moreover, the RWH system for toilet flushing is more expensive than that for only irrigation use, due to the installation costs related to the piping distribution system in the building.

In the present analysis, the costs related to the system maintenance were considered negligible when compared to purchase and installation costs [50]. With regard to operation costs and, in particular, the energy costs needed to pump the rainwater for the analyzed uses, these costs were neglected. Regarding this assumption, some considerations have to be made. In most of the sites in Sicily, water managers often adopt the intermittent distribution to cope with water shortage periods or to contain high water losses, due to the lack of adequate maintenance of the supply networks [52,53]. As a consequence, the plumbing systems of households are frequently equipped with pumping stations and private tanks to collect potable water during service periods and supply water when the service is not available. Because of the lack of confidence of users on the reliability of the water supply service, the private tanks and the pumping system are not bypassed, even if the distribution system operates on a continuous basis. Thus, the users are prepared for unexpected interruption of the supply service. Therefore, in most of the sites of Sicily, users nowadays have to pay a large amount for energy needed to draw water from the public network because of private storage tanks and pumping systems [54].

Table 4. Elements costs of a schematic RWH system for each tank size and rainwater use.

Item	Toilet Flushing			Irrigation			Toilet Flushing + Irrigation
Tank capacity [m3]	10	15	20	10	15	20	10	15	20
Cost for concrete tank purchase, the first flush device and their underground placing	€ 1778	€ 2284	€ 2991	€ 1700	€ 2284	€ 2991	€ 1700	€ 2284	€ 2991
Pipes drainage system inlet and outlet tank	€ 178	€ 178	€ 178	€ 178	€ 178	€ 178	€ 178	€ 178	€ 178
Piping system for not potable water supply	€ 194	€ 194	€ 194	€ 290	€ 290	€ 97	€ 290	€ 290	€ 290
Pump and PLC equipment	€ 2000	€ 2000	€ 2000	€ 2000	€ 2000	€ 1500	€ 2000	€ 2000	€ 2000
Rainwater filter	€ 220	€ 220	€ 250	€ 220	€ 220	€ 250	€ 220	€ 220	€ 250
Total costs	€ 4370	€ 4876	€ 5612	€ 4388	€ 4973	€ 5016	€ 4388	€ 4973	€ 5709

Table 4. Elements costs of a schematic RWH system for each tank size and rainwater use.

Item	Toilet Flushing			Irrigation			Toilet Flushing + Irrigation
Tank capacity [m3]	10	15	20	10	15	20	10	15	20
Cost for concrete tank purchase, the first flush device and their underground placing	€ 1778	€ 2284	€ 2991	€ 1700	€ 2284	€ 2991	€ 1700	€ 2284	€ 2991
Pipes drainage system inlet and outlet tank	€ 178	€ 178	€ 178	€ 178	€ 178	€ 178	€ 178	€ 178	€ 178
Piping system for not potable water supply	€ 194	€ 194	€ 194	€ 290	€ 290	€ 97	€ 290	€ 290	€ 290
Pump and PLC equipment	€ 2000	€ 2000	€ 2000	€ 2000	€ 2000	€ 1500	€ 2000	€ 2000	€ 2000
Rainwater filter	€ 220	€ 220	€ 250	€ 220	€ 220	€ 250	€ 220	€ 220	€ 250
Total costs	€ 4370	€ 4876	€ 5612	€ 4388	€ 4973	€ 5016	€ 4388	€ 4973	€ 5709

With regard to the benefits related to the RWH system installation, only the benefits due to the potable water saving have been considered. In particular, the financial benefit has been evaluated in terms of reduction of the annual water bill from water utilities. Even if relevant, in this analysis the environmental and social benefits have not been accounted. The cost-benefit analysis has been carried out according to the “Guide to cost-benefit analysis of investment projects” in Europe [55]. Namely, two performance indicators, the Net Present Value (NPV) and the payback period (PBP), have been evaluated, as described by Khastagir and Jayasuriya [50] and Matos et al. [56]. In the analysis, some assumptions have been made:

• The evaluation period to assess the NPV has been set equal to 20 years [8,56,57];
• according to [55], a discount rate of 5% has been assumed;
• the inflation rate has been assumed equal to 8% (on the basis of the inflation rate of potable water price in Italy in recent years);
• the actual price for potable water has been set equal to 2.5 €/m³ (obtained as the average of the actual prices adopted by different water utilities operating in Sicily).

The effect of the variability of annual yield related to the different location of the system installation has been accounted for in the PBP and the NPV appraisal, considering the minimum, the maximum and the mean annual yield in the area of study. Results are shown in Table 5 for each tank size and rainwater use. As expected, for a given use, the payback period increases with the tank capacity. For the toilet flushing use, a 10 m³ tank capacity was found to to be adequate, since an increase of the tank size of 5–10 m³ improves the system R_V of only the 1%. For a yield equal to the mean annual value, the payback period is 21 years (closer to the assumed evaluation period). As regards to irrigation use, the annual benefits are scarce, due to the lower annual yield values. As a consequence, payback periods are higher than the assumed evaluation period, specifically about 34 years for the three annual yield values, meaning that 20 years are enough to get back only half of the costs of system installation. In terms of annual R_V, a 20 m³ capacity was found to be a feasible solution for this use. For both uses, the payback period related to the mean annual yield are similar, as well as the system R_V. Therefore, in this case, the 10 m³ capacity seems to be the most advantageous.

Table 5. NPV and PBP values related to each tank size and different annual yields for each rainwater use.

Rainwater Use	Tank Volume	Investments/Costs	Annual Yield/Water Saving		Annual RV	NPV (20 Years)	PBP = NCER
	(m3)	(€)	(m3/year)		(%)	(€)	(year)
Toilet flushing	10	€ 4388	max	78	100%	€ 1,137	17
			mean	60	77%	−€ 134	21
			min	34	43%	−€ 1969	31
	15	€ 4973	max	78	100%	€ 631	19
			mean	61	78%	−€ 569	22
			min	34	43%	−€ 2476	34
	20	€ 5709	max	78	100%	−€ 106	21
			mean	61	78%	−€ 1306	25
			min	34	43%	−€ 3212	37
Irrigation	10	€ 3773	max	38	86%	−€ 1090	26
			mean	25.6	58%	−€ 1965	34
			min	13.4	30%	−€ 2827	50
	15	€ 4279	max	44.4	100%	−€ 1596	29
			mean	30.7	69%	−€ 2112	33
			min	15.2	34%	−€ 3206	50
	20	€ 5016	max	44.4	100%	−€ 1881	29
			mean	34.7	78%	−€ 2566	34
			min	15.2	34%	−€ 3943	55
Toilet flushing + Irrigation	10	€ 4370	max	94.5	77%	€ 2283	15
			mean	63.7	52%	€ 109	20
			min	33.9	28%	−€ 1995	32
	15	€ 4876	max	104.5	85%	€ 1699	16
			mean	65.5	53%	−€ 348	22
			min	33.9	28%	−€ 2579	34
	20	€ 5612	max	109.5	89%	€ 2022	16
			mean	66.5	54%	−€ 1014	24
			min	33.9	28%	−€ 3316	38

Table 5. NPV and PBP values related to each tank size and different annual yields for each rainwater use.

Rainwater Use	Tank Volume	Investments/Costs	Annual Yield/Water Saving		Annual RV	NPV (20 Years)	PBP = NCER
	(m3)	(€)	(m3/year)		(%)	(€)	(year)
Toilet flushing	10	€ 4388	max	78	100%	€ 1,137	17
			mean	60	77%	−€ 134	21
			min	34	43%	−€ 1969	31
	15	€ 4973	max	78	100%	€ 631	19
			mean	61	78%	−€ 569	22
			min	34	43%	−€ 2476	34
	20	€ 5709	max	78	100%	−€ 106	21
			mean	61	78%	−€ 1306	25
			min	34	43%	−€ 3212	37
Irrigation	10	€ 3773	max	38	86%	−€ 1090	26
			mean	25.6	58%	−€ 1965	34
			min	13.4	30%	−€ 2827	50
	15	€ 4279	max	44.4	100%	−€ 1596	29
			mean	30.7	69%	−€ 2112	33
			min	15.2	34%	−€ 3206	50
	20	€ 5016	max	44.4	100%	−€ 1881	29
			mean	34.7	78%	−€ 2566	34
			min	15.2	34%	−€ 3943	55
Toilet flushing + Irrigation	10	€ 4370	max	94.5	77%	€ 2283	15
			mean	63.7	52%	€ 109	20
			min	33.9	28%	−€ 1995	32
	15	€ 4876	max	104.5	85%	€ 1699	16
			mean	65.5	53%	−€ 348	22
			min	33.9	28%	−€ 2579	34
	20	€ 5612	max	109.5	89%	€ 2022	16
			mean	66.5	54%	−€ 1014	24
			min	33.9	28%	−€ 3316	38

4. Conclusions

For a long time, urban design and planning has ignored the advantages of RWH as a sustainable water resources management tool; however, interest in RWH systems as an alternative water source has recently increased. These systems can provide a supplementary water supply in urbanized areas when integrated with existing conventional water supply systems, or they can serve as the main water source in rural areas where the availability of water resources is a critical issue. Moreover, utilizing RWH represents an effective adaptive strategy to climate change against the reduction of water availability. The feasibility of rainwater harvesting in a particular locality is highly dependent on rainfall characteristics (intensity and frequency). Other variables, such as catchment area and type of catchment surface, usually can be modified to improve system performance.

In this study, a behavioral model was applied to assess the performance of an RWH system in terms of its reliability. Water demand for toilet flushing and garden irrigation and three years of historical daily rainfall data for 111 locations in Sicily were used as input to the system simulation model, the YAS algorithm. The analysis of simulation results, in terms of annual reliability of the RWH system, highlighted the possibility of obtaining good performances when the collected water is intended solely for toilet flushing. In this case, the saving of water from other supply systems makes the RWH system to be cost-effective in most of the analyzed territory. In particular, a storage capacity of 20 m³ is able to ensure the complete meeting of water demand for toilet flushing in a wide northern area of Sicily. On the other hand, the use of rainwater for garden irrigation requires, in most of the island, higher storage capacities in order to obtain advantageous performances in terms of water saving. Due to the different temporal patterns of water demands, the coupling of the two uses, toilet flushing and garden irrigation, is not particularly advantageous for the considered storage volumes and collection surfaces.

The analysis of the monthly variability of the RWH system’s reliability showed that the temporal variability of rainfall over the year has an important impact on storage volume. In an area with uniform monthly precipitation throughout the year, a smaller storage volume is necessary than that required in an area with a distinct seasonal precipitation distribution.

Results from the application of the YAS algorithm to different sites in Sicily were used to analyze the correlation between mean annual precipitation and the reliability of the examined RWH system. The analysis defined curves that are valid for the entire area of study and relate to the above mentioned variables. The equations of these curves represent a useful tool for practical application in Sicily, easily and quickly providing a value of the RWH reliability corresponding to a given value of mean annual rainfall. The uncertainty related to the obtained curves was assessed by reducing the original dataset and obtaining alternative curves. Future research can assess the implications of household occupancy and the impacts of rooftop and courtyard areas and storage capacity on reliability. These factors can then be integrated into the proposed equations to obtain general relationships to more effectively evaluate the performance of any RWH system.

A cost-benefit analysis has been performed, providing the Net Present Value and the payback periods on the capital cost of system installation. Results enabled the identification of the most feasible tank capacity. Despite the high payback periods of capital cost, the environmental and social advantages related to the use of RWH systems cannot be neglected. Indeed, these systems promote a more sustainable water use and a greater resilience to water scarcity.

Further analysis should also account for the effect of climate change on precipitation. The equations presented here are valid under the assumption that the mean annual precipitation will not be affected by variations in the next years. The existence of trends could significantly affect the performance of an RWH system. Specifically, the reduction of rainfall amount and the variation of rainfall temporal distribution over the year (in particular the concentration of annual rainfall in short periods) could lead to a considerable decrease of the system efficiency. Therefore, the design of RWH tanks should also involve an analysis of future climate scenarios derived from regional climate models.

In summary, RWH systems can play an important role in supplementing conventional water supply systems. For this reasons, incentives and government support could be important to encourage householders to adopt RWH water systems in residential urban areas.