Comparison of Four Different Energy Balance Models for Estimating Evapotranspiration in the Midwestern United States
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area

2.2. Energy Balance Models
| No. | Dataset | Symbol | Source | Resolution |
|---|---|---|---|---|
| 1 | Elevation | z | DEM | 30 m |
| 2 | Surface temperature | Ts | Landsat | 60/120 m |
| 3 | Normalized Difference Vegetation Index | - | Landsat | 30 m |
| 4 | Albedo | α | Landsat | 30 m |
| 5 | Momentum roughness length | Zom | NDVI | 30 m |
| 6 | Temperature difference | dT | Model | 1 km |
| 7 | Flux ET | - | Eddy covariance | - |
| 8 | Extraterrestrial solar radiation | Ra | Model | - |
| 9 | Alfalfa reference ET | ETr | Weather station | - |
| 10 | Grass reference ET | ETo | GDAS | 10 km |
2.2.1. The METRIC Model
2.2.2. SEBAL Model
2.2.3. SEBS Model
2.2.4. SSEBop Model
2.3. Models Validation
3. Results and Discussion
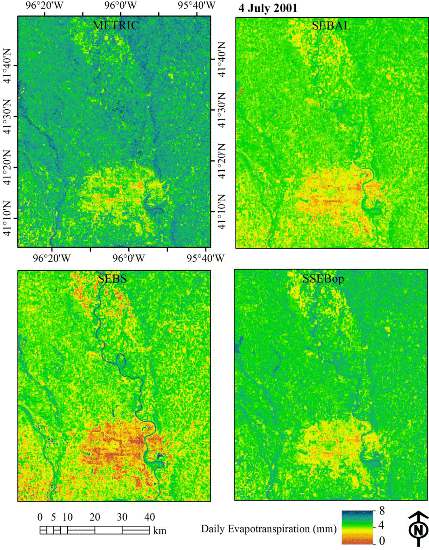
3.1. Spatial and Temporal Variation of ET Using the METRIC Model

| Date | 4 July 2001 | 5 August 2001 | 13 August 2001 | 29 August 2001 | 30 September 2001 | 16 October 2001 | 24 October 2001 | 11 December 2001 |
|---|---|---|---|---|---|---|---|---|
| Ke | 0.63 | 0 | 0 | 0.31 | 0.11 | 0.25 | 0.62 | 0.22 |
3.2. Spatial and Temporal Variation of ET Using the SEBAL Model

3.3. Spatial and Temporal Variation of ET Using the SEBS Model

3.4. Spatial and Temporal Variation of ET Using the SSEBop Model

| Date | 4 July 2001 | 5 August 2001 | 13 August 2001 | 29 August 2001 | 30 September 2001 | 16 October 2001 | 24 October 2001 | 11 December 2001 |
|---|---|---|---|---|---|---|---|---|
| ETo | 5.67 | 6.52 | 4.82 | 4.75 | 2.08 | 1.35 | 1.90 | 0.73 |
| ETr | 6.73 | 8.46 | 6.30 | 7.58 | 4.49 | 3.00 | 3.61 | 2.66 |
3.5. Spatial Variation of Evaporative Fraction from Different Models on Selected Dates


3.6. Comparison of Estimated ET with the Eddy Covariance Measurements

| Parameters | METRIC Model | SEBAL Model | SEBS Model | SSEBop Model | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mead Site 1 | Mead Site 2 | Mead Site 3 | Mead Site 1 | Mead Site 2 | Mead Site 3 | Mead Site 1 | Mead Site 2 | Mead Site 3 | Mead Site 1 | Mead Site 2 | Mead Site 3 | |
| r (-) | 0.97 | 0.97 | 0.94 | 0.88 | 0.93 | 0.92 | 0.91 | 0.94 | 0.83 | 0.97 | 0.95 | 0.95 |
| R2 (-) | 0.94 | 0.95 | 0.88 | 0.78 | 0.86 | 0.85 | 0.83 | 0.89 | 0.68 | 0.94 | 0.90 | 0.91 |
| RE (%) | 2.5 | 11.6 | 13.7 | −47.2 | −42.6 | −39.6 | −31.1 | −25.0 | −26.0 | −12.6 | −7.1 | −8.1 |
| MAE (mm·day−1) | 0.73 | 0.71 | 0.98 | 1.87 | 1.48 | 1.29 | 1.48 | 1.15 | 1.23 | 0.74 | 0.72 | 0.66 |
| MAE (%) | 18.44 | 19.81 | 29.90 | 47.63 | 41.26 | 39.59 | 37.64 | 31.84 | 37.60 | 18.85 | 20.00 | 20.26 |
| MBE (mm·day−1) | 0.10 | 0.46 | 0.45 | −1.86 | −1.67 | −1.29 | −1.22 | −0.96 | −0.85 | −0.50 | −0.22 | −0.27 |
| MBE (%) | 2.53 | 12.71 | 13.71 | −47.21 | −46.40 | −39.59 | −31.11 | −26.77 | −25.99 | −12.63 | −6.18 | −8.15 |
| RMSE (mm·day−1) | 0.88 | 0.84 | 1.06 | 2.46 | 2.01 | 1.74 | 1.96 | 1.53 | 1.67 | 0.90 | 0.88 | 0.73 |
| NSE (-) | 0.91 | 0.90 | 0.79 | 0.28 | 0.42 | 0.43 | 0.54 | 0.66 | 0.47 | 0.90 | 0.89 | 0.90 |
3.7. Comparison of Estimated ET for Selected Land Use/Land Cover




4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Pereira, L.S.; Allen, R.G.; Smith, M.; Raes, D. Crop evapotranspiration estimation with FAO56: Past and future. Agric. Water Manag. 2015, 147, 4–20. [Google Scholar] [CrossRef]
- Allen, R.; Irmak, A.; Trezza, R.; Hendrickx, J.M.H.; Bastiaanssen, W.; Kjaersgaard, J. Satellite-based ET estimation in agriculture using SEBAL and METRIC. Hydrol. Process. 2011, 25, 4011–4027. [Google Scholar] [CrossRef]
- Yan, H.; Wang, S.Q.; Billesbach, D.; Oechel, W.; Bohrer, G.; Meyers, T.; Martin, T.A.; Matamala, R.; Phillips, R.P.; Rahman, F.; et al. Improved global simulations of gross primary product based on a new definition of water stress factor and a separate treatment of C3 and C4 plants. Ecol. Model. 2015, 297, 42–59. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Camarero, J.J.; Zabalza, J.; Sanguesa-Barreda, G.; Lopez-Moreno, J.I.; Tague, C.L. Evapotranspiration deficit controls net primary production and growth of silver fir: Implications for Circum-Mediterranean forests under forecasted warmer and drier conditions. Agric. For. Meteorol. 2015, 206, 45–54. [Google Scholar] [CrossRef]
- Karlsson, I.B.; Sonnenborg, T.O.; Seaby, L.P.; Jensen, K.H.; Refsgaard, J.C. Effect of a high-end CO2-emission scenario on hydrology. Clim. Res. 2015, 64, 39–54. [Google Scholar] [CrossRef]
- Anderson, M.C.; hain, C.; Otkin, J.; Zhan, X.; Mo, K.; Svoboda, M.; Wardlow, B.; Pimstein, A. An intercomparison of drought indicators based on thermal remote sensing and NLDAS-2 simulations with U.S. drought monitor classifications. J. Hydrometeorol. 2013, 14, 1035–1056. [Google Scholar] [CrossRef]
- Yimam, Y.T.; Ochsner, T.E.; Kakani, V.G. Evapotranspiration partitioning and water use efficiency of switchgrass and biomass sorghum managed for biofuel. Agric. Water Manag. 2015, 155, 40–47. [Google Scholar] [CrossRef]
- Spies, R.R.; Franz, K.J.; Hogue, T.S.; Bowman, A.L. Distributed hydrologic modeling using satellite-derived potential evapotranspiration. J. Hydrometeorol. 2015, 16, 129–146. [Google Scholar] [CrossRef]
- Snyder, R.L.; Pedras, C.; Montazar, A.; Henry, J.M.; Ackley, D. Advances in ET-based landscape irrigation management. Agric. Water Manag. 2015, 147, 187–197. [Google Scholar] [CrossRef]
- Nolan, R.H.; Lane, P.N.J.; Benyon, R.G.; Bradstock, R.A.; Mitchell, P.J. Trends in evapotranspiration and streamflow following wildfire in resprouting eucalypt forests. J. Hydrol. 2015, 524, 614–624. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Karimi, P.; Rebelo, L.M.; Duan, Z.; Senay, G.; Muthuwatte, L.; Smakhtin, V. Earth observation based assessment of the water production and water consumption of Nile Basin agro-ecosystems. Remote Sens. 2014, 6, 10306–10334. [Google Scholar] [CrossRef]
- Gowda, P.H.; Chavez, J.L.; Colaizzi, P.D.; Evett, S.R.; Howell, T.A.; Tolk, J.A. ET mapping for agricultural water management: Present status and challenges. Irrig. Sci. 2008, 26, 223–237. [Google Scholar] [CrossRef]
- Glenn, E.P.; Nagler, P.L.; Huete, A.R. Vegetation Index Methods for estimating evapotranspiration by remote sensing. Surv. Geophys. 2010, 31, 531–555. [Google Scholar] [CrossRef]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating land surface evaporation: A review of methods using remotely sensed surface temperature data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M. Regionalization of Surface Flux Densities and Moisture Indicators in Composite Terrain: A Remote Sensing Approach under Clear Skies in Mediterranean Climates; Report 109; DLO The Winand Staring Centre: Wageningen, The Netherlands, 1995. [Google Scholar]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A remote sensing surface energy balance algorithm for land (SEBAL)—1. Formulation. J. Hydrol. 1998, 212, 198–212. [Google Scholar] [CrossRef]
- Su, Z. The Surface Energy Balance System (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–99. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (METRIC)—Model. J. Irrig. Drain. Eng. 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Senay, G.B.; Bohms, S.; Singh, R.K.; Gowda, P.H.; Velpuri, N.M.; Alemu, H.; Verdin, J.P. Operational evapotranspiration mapping using remote sensing and weather datasets: A new parameterization for the SSEB approach. J. Am. Water Resour. Assoc. 2013, 49, 577–591. [Google Scholar] [CrossRef]
- Singh, R.; Senay, G.; Velpuri, N.; Bohms, S.; Scott, R.; Verdin, J. Actual evapotranspiration (water use) assessment of the Colorado River Basin at the Landsat resolution using the Operational Simplified Surface Energy Balance Model. Remote Sens. 2013, 6, 233–256. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Noordman, E.J.M.; Pelgrum, H.; Davids, G.; Thoreson, B.P.; Allen, R.G. SEBAL model with remotely sensed data to improve water-resources management under actual field conditions. J. Irrig. Drain. Eng. 2005, 131, 85–93. [Google Scholar] [CrossRef]
- Ershadi, A.; McCabe, M.F.; Evans, J.P.; Chaney, N.W.; Wood, E.F. Multi-site evaluation of terrestrial evaporation models using FLUXNET data. Agric. For. Meteorol. 2014, 187, 46–61. [Google Scholar] [CrossRef]
- French, A.N.; Hunsaker, D.J.; Thorp, K.R. Remote sensing of evapotranspiration over cotton using the TSEB and METRIC energy balance models. Remote Sens. Environ. 2015, 158, 281–294. [Google Scholar] [CrossRef]
- Irmak, S.; Istanbulluoglu, E.; Irmak, A. An evaluation of evapotranspiration model complexity against performance in comparison with Bowen ratio energy balance measurements. Trans. ASABE 2008, 51, 1295–1310. [Google Scholar] [CrossRef]
- Li, S.; Zhang, L.; Kang, S.; Tong, L.; Du, T.; Hao, X.; Zhao, P. Comparison of several surface resistance models for estimating crop evapotranspiration over the entire growing season in arid regions. Agric. For. Meteorol. 2015, 208, 1–15. [Google Scholar] [CrossRef]
- Lu, J.; Sun, G.; McNulty, S.G.; Amatya, D.M. A comparison of six potential evapotranspiration methods for regional use in the southeastern United States. J. Am. Water Resour. Assoc. 2005, 41, 621–633. [Google Scholar] [CrossRef]
- Gonzalez-Dugo, M.P.; Neale, C.M.U.; Mateos, L.; Kustas, W.P.; Prueger, J.H.; Anderson, M.C.; Li, F. A comparison of operational remote sensing-based models for estimating crop evapotranspiration. Agric. For. Meteorol. 2009, 149, 1843–1853. [Google Scholar] [CrossRef]
- Orth, R.; Staudinger, M.; Seneviratne, S.I.; Seibert, J.; Zappa, M. Does model performance improve with complexity? A case study with three hydrological models. J. Hydrol. 2015, 523, 147–159. [Google Scholar] [CrossRef]
- El Tahir, M.E.H.; Wenzhong, W.; Xu, C.Y.; Youjing, Z.; Singh, V.P. Comparison of methods for estimation of regional actual evapotranspiration in data scarce regions: Blue Nile Region, Eastern Sudan. J. Hydrol. Eng. 2012, 17, 578–589. [Google Scholar] [CrossRef]
- Wilson, K.B.; Hanson, P.J.; Mulholland, P.J.; Baldocchi, D.D.; Wullschleger, S.D. A comparison of methods for determining forest evapotranspiration and its components: Sap-flow, soil water budget, eddy covariance and catchment water balance. Agric. For. Meteorol. 2001, 106, 153–168. [Google Scholar] [CrossRef]
- Consoli, S.; Vanella, D. Comparisons of satellite-based models for estimating evapotranspiration fluxes. J. Hydrol. 2014, 513, 475–489. [Google Scholar] [CrossRef]
- Chen, Y.; Xia, J.; Liang, S.; Feng, J.; Fisher, J.B.; Li, X.; Li, X.; Liu, S.; Ma, Z.; Miyata, A.; et al. Comparison of satellite-based evapotranspiration models over terrestrial ecosystems in China. Remote Sens. Environ. 2014, 140, 279–293. [Google Scholar] [CrossRef]
- Verma, S.B.; Dobermann, A.; Cassman, K.G.; Walters, D.T.; Knops, J.M.; Arkebauer, T.J.; Suyker, A.E.; Burba, G.G.; Amos, B.; Yang, H.; et al. Annual carbon dioxide exchange in irrigated and rainfed maize-based agroecosystems. Agric. For. Meteorol. 2005, 131, 77–96. [Google Scholar] [CrossRef]
- Su, H.; McCabe, M.F.; Wood, E.F.; Su, Z.; Prueger, J.H. Modeling evapotranspiration during SMACEX: Comparing two approaches for local- and regional-scale prediction. J. Hydrometeorol. 2005, 6, 910–922. [Google Scholar] [CrossRef]
- Foken, T.; Aubinet, M.; Finnigan, J.J.; Leclerc, M.Y.; Mauder, M.; Paw, U.K.T. Results of a panel discussion about the energy balance closure correction for trace gases. Bull. Am. Meteorol. Soc. 2011, 92. [Google Scholar] [CrossRef]
- Singh, R.K.; Irmak, A. Treatment of anchor pixels in the METRIC model for improved estimation of sensible and latent heat fluxes. Hydrol. Sci. J. 2011, 56, 895–906. [Google Scholar] [CrossRef]
- Long, D.; Singh, V.P. Assessing the impact of end-member selection on the accuracy of satellite-based spatial variability models for actual evapotranspiration estimation. Water Resour. Res. 2013, 49, 2601–2618. [Google Scholar] [CrossRef]
- Paul, G.; Gowda, P.H.; Vara Prasad, P.V.; Howell, T.A.; Staggenborg, S.A.; Neale, C.M.U. Lysimetric evaluation of SEBAL using high resolution airborne imagery from BEAREX08. Adv. Water Resour. 2013, 59, 157–168. [Google Scholar] [CrossRef]
- Mahour, M.; Stein, A.; Sharifi, A.; Tolpekin, V. Integrating super resolution mapping and SEBS modeling for evapotranspiration mapping at the field scale. Precis. Agric. 2015, 16, 571–586. [Google Scholar] [CrossRef]
- Chavez, J.L.; Neale, C.M.U.; Prueger, J.H.; Kustas, W.P. Daily evapotranspiration estimates from extrapolating instantaneous airborne remote sensing ET values. Irrig. Sci. 2008, 27, 67–83. [Google Scholar] [CrossRef]
- Colaizzi, P.D.; Evett, S.R.; Howell, T.; Tolk, J.A. Comparison of five models to scale daily evapotranspiration from one-time-of-day measurements. Trans. Am. Soc. Agric. Eng. 2006, 49, 1409–1419. [Google Scholar] [CrossRef]
- Cammalleri, C.; Anderson, M.C.; Kustas, W.P. Upscaling of evapotranspiration fluxes from instantaneous to daytime scales for thermal remote sensing applications. Hydrol. Earth Syst. Sci. 2014, 18, 1885–1894. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.C.; Wu, J.W.; Wu, H.Y.; Chen, H.R.; Zhang, T. Improving temporal extrapolation for daily evapotranspiration using radiation measurements. J. Appl. Remote Sens. 2013, 7. [Google Scholar] [CrossRef]
- Timmermans, J.; Su, Z.; van der Tol, C.; Verhoef, A.; Verhoef, W. Quantifying the uncertainty in estimates of surface-atmosphere fluxes through joint evaluation of the SEBS and SCOPE models. Hydrol. Earth Syst. Sci. 2013, 17, 1561–1573. [Google Scholar] [CrossRef]
- Velpuri, N.M.; Senay, G.B.; Singh, R.K.; Bohms, S.; Verdin, J.P. A comprehensive evaluation of two MODIS evapotranspiration products over the conterminous United States: Using point and gridded FLUXNET and water balance ET. Remote Sens. Environ. 2013, 139, 35–49. [Google Scholar] [CrossRef]
- Senay, G.B.; Verdin, J.P.; Lietzow, R.; Melesse, A.M. Global daily reference evapotranspiration modeling and evaluation. J. Am. Water Resour. Assoc. 2008, 44, 969–979. [Google Scholar] [CrossRef]
- Timmermans, W.J.; Kustas, W.P.; Anderson, M.C.; French, A.N. An intercomparison of the surface energy balance algorithm for land (SEBAL) and the two-source energy balance (TSEB) modeling schemes. Remote Sens. Environ. 2007, 108, 369–384. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, R.K.; Senay, G.B. Comparison of Four Different Energy Balance Models for Estimating Evapotranspiration in the Midwestern United States. Water 2016, 8, 9. https://doi.org/10.3390/w8010009
Singh RK, Senay GB. Comparison of Four Different Energy Balance Models for Estimating Evapotranspiration in the Midwestern United States. Water. 2016; 8(1):9. https://doi.org/10.3390/w8010009
Chicago/Turabian StyleSingh, Ramesh K., and Gabriel B. Senay. 2016. "Comparison of Four Different Energy Balance Models for Estimating Evapotranspiration in the Midwestern United States" Water 8, no. 1: 9. https://doi.org/10.3390/w8010009
APA StyleSingh, R. K., & Senay, G. B. (2016). Comparison of Four Different Energy Balance Models for Estimating Evapotranspiration in the Midwestern United States. Water, 8(1), 9. https://doi.org/10.3390/w8010009