Regional Patterns of Baseflow Variability in Mexican Subwatersheds
Abstract
:1. Introduction
2. Materials and Methods
2.1. Input Data
2.2. Recession Curves’ Selection
2.3. Spatial Predictors of the Response of Baseflow and Symmetry in the Process
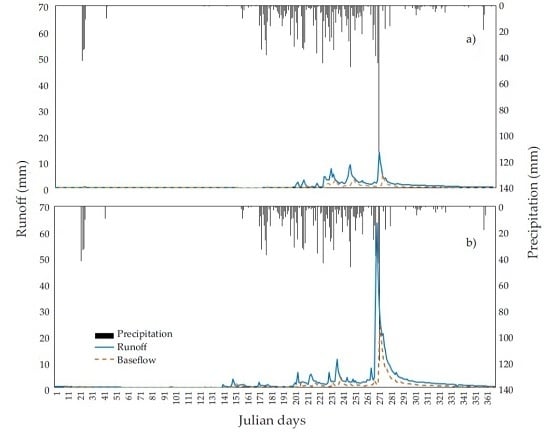
2.4. Baseflow Separation
3. Results
3.1. Recession Curves
3.2. Baseflow Response Spatial Predictors
3.3. Baseflow Separation
4. Discussion
4.1. Recession Curve
4.2. Baseflow Spatial Patterns and Model Parameterization
4.3. Baseflow Separation
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Campolo, M.; Soldati, A.; Andreussi, P. Forecasting river flow rate during low-flow periods using neural networks. Water Resour. Res. 1999, 35, 3547–3552. [Google Scholar] [CrossRef]
- Van Dijk, A.I. Climate and terrain factors explaining streamflow response and recession in Australian catchments. Hydrol. Earth Syst. Sci. 2010, 14, 159–169. [Google Scholar] [CrossRef]
- Beck, H.L.; van Dijt, A.; Miralles, D.G.; McVicar, T.R.; Schellekens, J. Global patterns in baseflow index and recession based on streamflow observations from 3394 catchments. Water Resour. Res. 2013, 49, 7843–7863. [Google Scholar] [CrossRef]
- Budyko, M.I. Climate and Life; Academics: New York, NY, USA, 1974. [Google Scholar]
- Fu, B.P. On the calculation of the evaporation from land surface. Sci. Atmos. 1981, 1, 23–31. (In Chinese) [Google Scholar]
- Zhang, L.; Dawes, W.R.; Walker, G.R. Response of mean annual evapotranspiration to vegetation changes at catchment scale. Water Resour. Res. 2001, 3, 701–708. [Google Scholar] [CrossRef]
- Gerrits, A.M.J.; Savenije, H.H.G.; Veling, E.J.M.; Pfister, L. Analytical derivation of the Budyko curve based on rainfall characteristics and a simple evaporation model. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Troch, P.A.; Carrillo, G.; Sivapalan, M.; Wagener, T.; Sawlez, K. Climate-vegetation-soil interactions and long-term hydrologic partitioning: Signatures of catchment co-evolution. Hydrol. Earth Syst. Sci. 2013, 17, 2209–2217. [Google Scholar] [CrossRef]
- Wang, L.; Wu, L. Similarity of climate control on baseflow and perennial stream density in the Budyko framework. Hydrol. Earth Syst. Sci. 2013, 17, 315–324. [Google Scholar] [CrossRef]
- Santhi, C.; Allen, P.; Muttiah, M.R.S.; Arnold, J.G.; Tuppad, P. Regional estimation of base flow for the conterminous United States by hydrologic landscape regions. J. Hydrol. 2008, 351, 139–153. [Google Scholar] [CrossRef]
- Longobardi, A.; Villani, P. Baseflow index regionalization analysis in a mediterranean area and data scarcity context: Role of the catchment permeability index. J. Hydrol. 2008, 355, 63–75. [Google Scholar] [CrossRef]
- Wang, T.; Istanbulluoglu, E.; Lenters, J.; Scott, D. On the role of groundwater and soil texture in the regional water balance: An investigation of Nebraska Sand Hills. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Istanbulluoglu, E.; Tiejun, W.; Wright, O.; Lenters, J.D. Interpretation of hydrologic trends from a water balance perspective: The role of groundwater storage in the Budyko’s hypothesis. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Sivapalan, M. Pattern, process and function: Elements of a unified theory of hydrology at the catchment scale. In Encyclopedia of Hydrological Sciences; Jhon Wiley Ltd.: West Sussex, UK, 2005; Chapter 13; pp. 193–219. [Google Scholar]
- Ponce, V.M.; Shetty, A.V. A conceptual model of catchment water balance: Formulation and calibration. J. Hydrol. 1995, 173, 27–40. [Google Scholar] [CrossRef]
- Sivapalan, M.; Yaeger, M.A.; Ciaran, H.J.; Xiangyu, X.; Troch, P.A. Functional model of wáter balance variablity at the catchment scale: 1. Evidence of hydrologic similiraty and space-time symmetry. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Harman, C.J.; Troch, P.A.; Sivapalan, M. Functional model of water balance variability at the catchment scale: 2. Elasticity of fast and slow runoff components to precipitation change in the continental United States. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Tallaksen, L. A review of baseflow recession analisys. J. Hydrol. 1995, 165, 349–370. [Google Scholar] [CrossRef]
- Eckhardt, K. How to construct recursive digital filters for Baseflow separation. Hydrol. Process. 2005, 19, 507–515. [Google Scholar] [CrossRef]
- Huyck, A.; Pauwels, V.; Vershoest, N. A baseflow separation algorithm based on the linearized boussinesq equation for complex hillslopes. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- He, S.; Li, S.; Xie, R.; Lu, J. Baseflow separation based on a metereology corrected nonlinear algorithm in typical rainy agricultural watershed. J. Hydrol. 2016, 535, 418–428. [Google Scholar] [CrossRef]
- Paz, F.; Odi, M.; Cano, A.; Bolaños, M.; Zarco, A. Equivalencia ambiental en la productividad de la vegetación. Agrociencia 1999, 43, 635–648. (In Spanish) [Google Scholar]
- Banco Nacional de Datos de Aguas Superficiales, 2011. Consulta de Datos Hidrométricos, de Presas y Sedimentos. Comisión Nacional del Agua: México. Available online: www.conagua.gob.mx/CONAGUA07/contenido/documentos/portada%20bandas.htm (accessed on 25 January 2015).
- García, E. Climas, 1:4000 000. IV.4.10 (A). Atlas Nacional de México Vol. II; Instituto de Geografía, UNAM.: Ciudad de México, México, 1990. (In Spanish) [Google Scholar]
- Instituto Nacional de Estadística, Geografía e Informática (INEGI). Red Hidrográfica Escala 1:50,000 Edición 2.0. Available online: http://www.inegi.org.mx/geo/contenidos/topografia/regiones_hidrograficas.aspx (accessed on 16 Junuary 2016).
- Comisión Nacional para el Conocimiento y Uso de la Biodiversidad (CONABIO). Subcuencas Hidrológicas. Available online: http://www.conabio.gob.mx/informacion/metadata/gis/subcu1mgw.xml?_httpcache=yes&_xsl=/db/metadata/xsl/fgdc_html.xsl&_indent=no (accessed on 15 January 2015).
- Programa Mexicano del Carbono (PMC). Digitalización de Subcuencas Escala 1,50000; Programa Mexicano del Carbono: Texcoco, Estado de México, México, 2014. [Google Scholar]
- Secretaria de Recursos Hidráulicos (SRH). Boletines Hidrológicos; Gerencia de Aguas Superficiales: Ciudad de México, México, 1970.
- Programa Mexicano del Carbono (PMC). Malla Climática Nacional; Programa Mexicano del Carbono (PMC): Texcoco, México, 2015. (In Spanish) [Google Scholar]
- Hargreaves, G.H.; Samani, Z.A. Reference crop evapotranspiration from temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Food and Agriculture Organization of the United Nations (FAO). Harmonized Database of Soil. Available online: http://www.fao.org/soils-portal/levantamiento-de-suelos/mapas-historicos-de-suelos-y-bases-de-datos/base-de-datos-armonizada-de-los-suelos-del-mundo-v12/es/ (accessed on 10 January 2015).
- Wittenberg, H. Nonlinear analysis of flow recession curves. IAHS Publ. 1994, 221, 61–67. [Google Scholar]
- Wittenberg, H. Baseflow recession and recharge as nonlinear storage processes. Hydrol. Process. 1999, 13, 715–726. [Google Scholar]
- Aksoy, H.; Wittenberg, H. Nonlinear baseflow recession analysis in watersheds with intermittent streamflow. Hydrol. Sci. J. 2011, 56, 226–237. [Google Scholar] [CrossRef]
- Gan, R.; Luo, Y. Using the nonlinear aquifer storage-discharge relationship to simulate the baseflow of glacir—And snowmelt-dominated basins in northwest China. Hydrol. Earth Syst. Sci. 2013, 17, 3577–3586. [Google Scholar] [CrossRef]
- Aksoy, H.; Wittenberg, H. Baseflow Recession Analysis for Flood-Prone Black Sea Watersheds in Turkey. Clean Air Soil Water 2015, 42, 1–10. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Prediction, Inference and Data Mining, 2nd ed.; Springer Verlag: New York, NY, USA, 2009. [Google Scholar]
- Salas, A.V.; Paz, F.; Macedo, C.; Ortiz, C.; Palacios, E. Modelación no lineal del flujo base en tres subcuencas de México. Terra Latinoam. 2015, 33, 285–297. (In Spanish) [Google Scholar]
- Comisión Nacional del Agua (CONAGUA). Determinación de la Disponibilidad de Agua Subterránea en el Acuífero 0859; Subdirección General Técnica de Aguas Subterraneas: Madera, México, 2013. [Google Scholar]
- Comisión Nacional del Agua (CONAGUA). Actualización de la Disponibilidad de Agua Subterránea en el Acuífero 1802; Subdirección General Técnica de Aguas Subterraneas: San Pedro Tuxpan, México, 2009. [Google Scholar]
- Comisión Nacional del Agua (CONAGUA). Actualización de la Disponibilidad de Agua Subterránea En el Acuífero 1502; Subdirección General Técnica de Aguas Subterraneas: Ixtlahuaca-Atlacomulco, México, 2009. [Google Scholar]
- Comisión Nacional del Agua (CONAGUA). Determinación de la Disponibilidad de Agua en el Acuífero 1701; Subdirección General Técnica de Aguas Subterraneas: Cuernavaca, México, 2013. [Google Scholar]
- Comisión Nacional del Agua (CONAGUA). Actualización de la Disponibilidad Media Anual de Agua Subterránea Acuífero 0711; Subdirección General técnica de Aguas Subterraneas: Arriaga-Pijijiapan, México, 2009. [Google Scholar]
- Comisión Nacional del Agua (CONAGUA). Actualización de la Disponibilidad de Agua Subterránea en el Acuífero 0512; Subdirección General Técnica de Aguas Subterraneas: Región Carbonífera, México, 2013. [Google Scholar]
- Comisión Nacional del Agua (CONAGUA). Actualización de la Disponibilidad de Agua Subterránea en el Acuífero 0507; Subdirección General Técnica de Aguas Subterraneas: Monclova, México, 2013. [Google Scholar]
- Sivapalan, M. Prediction of ungauged basin: A gran challenge for theoretical hydrology. Hydrol. Process. 2003, 17, 3163–3170. [Google Scholar] [CrossRef]
- Pedersen, T.J.; Peters, J.C.; Helweg, O. Hydrographs by single linear reservoir model. J. Hydraul. Div. ASCE 1980, 106, 837–852. [Google Scholar]
- Thomas, B.; Voegel, R.; Famiglietti, J. Objetive hydrograph Baseflow recession analysis. J. Hydrol. 2015, 525, 102–112. [Google Scholar] [CrossRef]
- Stewart, M.K. Promising new Baseflow separation and recession analysis methods applied to streamflow at Glendhu Catchment, New Zealand. Hydrol. Earth Syst. Sci. 2015, 19, 2587–2603. [Google Scholar] [CrossRef]
- Wittenberg, H. Effects of season and man-made changes on baseflow and flow recession: Case studies. Hydrol. Process. 2003, 17, 2113–2123. [Google Scholar] [CrossRef]
- Wittenberg, H.; Sivapalan, M. Watershed groundwater balance estimation using streamflow recession analysis and baseflow separation. J. Hydrol. 2003, 219, 20–33. [Google Scholar] [CrossRef]
- Dralle, D.; Karst, N.; Thompson, S. a, b careful: The challenge of scale invariance for comparative analyses in power law models of the streamflow recession. Geophys. Res. Lett. 2015, 42, 9285–9293. [Google Scholar] [CrossRef]
- Carmona, A.M.; Sivalapan, M.; Yaeger, M.A.; Poveda, G. Regional patterns variability of catchment water balances across the continental U.S.: A Budyko framework. Water Resour. Res. 2014, 50. [Google Scholar] [CrossRef]
- Peña-Arancibia, J.L.; van Dijk, A.I.J.M.; Mulligan, M.; Bruijnzeel, L.A. The role of climatic and terrain attributes in estimating baseflow recession in tropical catchments. Hydrol. Earth Syst. Sci. 2010, 14, 2193–2205. [Google Scholar] [CrossRef]
- Lacey, G.; Grayson, R. Relating baseflow to catchment properties in south-eastern Australia. J. Hydrol. 1998, 204, 231–250. [Google Scholar] [CrossRef]
- Fan, Y.; Chen, Y.; Li, W. Increasing precipitation and baseflow in Aksu River since 1950s. Quat. Int. 2014, 336, 26–34. [Google Scholar] [CrossRef]
- Sanchez, R.; Brooks, E.; Elliot, W.; Gazel, E.; Boll, J. Baseflow recession analysis in the inland Pacific Northwest of the United States. Hydrogeol. J. 2015, 23, 287–303. [Google Scholar] [CrossRef]
- Haberlandt, U.; Klocking, B.; Krysanova, V.; Becker, A. Regionalisation of the baseflow indexfrom dynamically simulated flow components—A case study in the Elbe River Basin. J. Hydrol. 2001, 248, 35–53. [Google Scholar] [CrossRef]
- Yang, D.; Shao, W.; Yeh, P.; Yang, H.; Kanae, S.; Oki, T. Impact of vegetation coverage on regional water balance in the nonhumid regions of China. Water Resour. Res. 2009, 45, 1–13. [Google Scholar] [CrossRef]
- Tague, C.; Grant, G.E. A geological framework for interpreting the low-flow regimes of Cascade streams, Willamette River Basin, Oregon. Water Resour. Res. 2004, 40, 150–178. [Google Scholar] [CrossRef]
- Price, K. Effects of watershed topography, soils, land use and climate on baseflow hydrology in humid regions: A review. Prog. Phys. Geogr. 2011, 4, 465–492. [Google Scholar] [CrossRef]
- Walton, W.C. Ground Water Recharge and Runoff in Illinois; Report of Investigation; Illinois State Water Survey; State Water Survey Division: Champaign, IL, USA, 1965; p. 55. [Google Scholar]
- Voepel, H.; Rudell, B.; Shumer, R.; Troch, P.; Brooks, P.; Neal, A.; Durcik, M.; Sivapalan, M. Quantifying the role climate and landscape characteristics on hydrologic partitioning and vegetation response. Water Resour. Res. 2011, 47, 1–13. [Google Scholar] [CrossRef]
- Brooks, P.D.; Troch, P.A.; Durcik, M.; Gallo, E.L.; Moravec, B.G.; Schlegel, M.E.; Carlson, M. Quantifying regional-scale ecosystem response to changes in precipitation: Not all rain is created equal. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Paz, F.; Odi, M.; Cano, A.; Lopez, E.; Bolaños, M.; Zarco, A.; Palacios, E. Elementos para el desarrollo de una hidrologia operacional con sensors remotos: Mezcla suelo-vegetación. Tecnol. Cienc. Agua 2009, 24, 69–80. [Google Scholar]
- Caro, R.; Eagleson, P.S. Estimating aquifer recharge due to rainfall. J. Hydrol. 1981, 53, 185–211. [Google Scholar] [CrossRef]
- Bart, R.; Hope, A. Inter-seasonal variability in base flow recession rates: The role of aquifer antecedent storage in central California watersheds. J. Hydrol. 2014, 519, 205–213. [Google Scholar] [CrossRef]
- Gholami, V.; Chau, K.; Fadaee, F.; Torkaman, J.; Ghaffari, A. Modeling of groundwater level fluctuations using dendrochronology in alluvial aquifers. J. Hydrol. 2015, 529, 1060–1069. [Google Scholar] [CrossRef]
- Archontoulis, S.; Miguez, F. Nonlinear regression models and applications in agricultural research. Agron. J. 2015, 105, 1–13. [Google Scholar] [CrossRef]







| Hydrometric Station | Aquifer Identifier | Aquifer Type | Transmissivity (m2·s−1) | Rock Type |
|---|---|---|---|---|
| 9080 | 0859 [39] | unconfined | 0.0241 | Riolite-tuff-acid, basalt, alluvial |
| 11,012 | 1802 [40] | unconfined | 0.0131 | Riolite-tuff-acid, basalt, alluvial |
| 12,601 | 1502 [41] | unconfined | 0.0370 | Alluvial, riolite |
| 18,271 | 1701 [42] | unconfined | 0.0180 | Basalt, sandstone |
| 23,022 | 0711 [43] | unconfined | 0.0018 | Basalt |
| 24,038 | 0512 [44] | unconfined | 0.1761 | Limestone, sandstone |
| 24,150 | 0507 [45] | unconfined | 0.0902 | Alluvial, limestone |
| Hydrometric Station | Subwatershed Name | Longitude (°) | Latitude (°) | Number of Recessions | Surface (km2) | Fitted Value | R2 |
|---|---|---|---|---|---|---|---|
| 9010 | R. Bavispe-Angostura | −109.36 | 30.61 | 3 | 14,188 | 6.4 | 0.92 |
| 9080 | R. Papigochic | −108.30 | 29.13 | 4 | 1856 | 14.3 | 0.96 |
| 10,098 | R. Alamos | −108.76 | 26.59 | 4 | 1813 | 12.7 | 0.91 |
| 11,012 | R. San Pedro | −105.14 | 21.96 | 4 | 11,924 | 36.0 | 0.92 |
| 15,010 | R. Purificación | −104.50 | 19.56 | 4 | 168 | 54.8 | 0.93 |
| 18,157 | R, Atoyac | −98.23 | 19.23 | 6 | 258 | 125.3 | 0.95 |
| 18,169 | R. Tilostoc | −100.11 | 19.17 | 4 | 154 | 212.6 | 0.93 |
| 18,271 | R. Apatlaco | −99.22 | 18.84 | 6 | 364 | 15.3 | 0.88 |
| 18,466 | R. Tilostoc-Anahuac | −100.25 | 19.27 | 3 | 124 | 100.0 | 0.91 |
| 18,489 | R. Tilostoc-set | −100.12 | 19.22 | 3 | 317 | 113.4 | 0.95 |
| 23,011 | R. Zanatenco | −93.74 | 16.08 | 6 | 166 | 43.0 | 0.96 |
| 23,022 | R. Sesecapa | −92.87 | 15.46 | 3 | 125 | 90.9 | 0.90 |
| 24,038 | R. Salado | −100.13 | 27.22 | 3 | 23,475 | 4.0 | 0.97 |
| 24,150 | R. Salado de Nadadores | −100.94 | 27.42 | 6 | 21,520 | 25.0 | 0.94 |
| 24,198 | R. Monterrey | −100.36 | 25.66 | 6 | 5412 | 91.0 | 0.94 |
| 26,268 | R. Tampán | −99.21 | 21.65 | 4 | 8722 | 22.0 | 0.92 |
| 27,083 | R. Necaxa | −97.87 | 20.25 | 5 | 562 | 140.3 | 0.98 |
| 28,135 | R. Papaloapan | −95.84 | 18.30 | 3 | 20,263 | 87.5 | 0.92 |
| 30,067 | R. San Pedro Mar | −93.09 | 16.06 | 5 | 42 | 235.0 | 0.92 |
| 12,574 | R. Gavia | −99.87 | 19.42 | 5 | 37 | 3.5 | 0.93 |
| 12,601 | R. Sila | −99.71 | 19.77 | 3 | 36 | 12.5 | 0.96 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salas-Aguilar, V.; Macedo-Cruz, A.; Paz, F.; Palacios, E.; Ortiz, C.; Quevedo, A. Regional Patterns of Baseflow Variability in Mexican Subwatersheds. Water 2016, 8, 98. https://doi.org/10.3390/w8030098
Salas-Aguilar V, Macedo-Cruz A, Paz F, Palacios E, Ortiz C, Quevedo A. Regional Patterns of Baseflow Variability in Mexican Subwatersheds. Water. 2016; 8(3):98. https://doi.org/10.3390/w8030098
Chicago/Turabian StyleSalas-Aguilar, Víctor, Antonia Macedo-Cruz, Fernando Paz, Enrique Palacios, Carlos Ortiz, and Abel Quevedo. 2016. "Regional Patterns of Baseflow Variability in Mexican Subwatersheds" Water 8, no. 3: 98. https://doi.org/10.3390/w8030098
APA StyleSalas-Aguilar, V., Macedo-Cruz, A., Paz, F., Palacios, E., Ortiz, C., & Quevedo, A. (2016). Regional Patterns of Baseflow Variability in Mexican Subwatersheds. Water, 8(3), 98. https://doi.org/10.3390/w8030098