Multi-Criteria Framework to Assess Large Scale Water Resources Policy Measures

Abstract

In order to assess water efficiency options on the European scale, a multi-criteria integrative hydro-economic modeling framework has been developed. With this framework, it is possible to assess combinations of measures which could help reducing the gap between water demand and water availability, while taking into account ecological, water quality, flood risk and economic aspects. The assessed measures include water retention, water savings and nutrient reduction measures. The presented work was carried out within the framework of the “Blueprint to safeguard Europe’s waters” policy initiative of the European Commission. Contrary to earlier studies concentrating on single measures in single river basins, this study shows that this modeling environment can evaluate combinations of measures in multiple river basins that meet the considered objectives, and in general can improve various water quantity and quality indicators as compared to the baseline situation. However, additional work is needed on for example quantifying the economics of damage and benefits before the modelling environment may be used for policy advice.

1. Introduction

At present, having sufficient water available for all usages with sufficient quality is a grand challenge. Water resources are constantly subject to various threats, such as over-exploitation of both surface and groundwater due to increased demographic and economic pressure and variable availability of water due to climatic changes, amongst others [1,2]. Water quality has also, in general, been rapidly deteriorating in the past years, mainly due to increasing contamination of water bodies from point and diffuse sources of pollution, unsustainable use of ground water, and improper water resources management [3].

In this context, it is important to develop and to apply new management strategies and methodologies aiming to reverse the trend of water quantity and quality degradation. Matching water availability and demand is one of the major challenges that policy makers and researchers are currently facing worldwide. The efficient and effective management of water resources is as much a political as a scientific issue [4].

Most existing projects have suggested partial approaches that examine only a single measure at local scales. The added value of this paper is that we evaluate optimum combinations of measures for multiple river basins with an integrative multi criteria methodological tool. It should be stated here that each river basin will yield its own unique set of measures, optimized against local conditions.

In the year 2000, the European Union adopted the Water Framework Directive (WFD) [5]. The WFD is an integrated approach to reach a common EU water policy centered on the river basin, which has as its main aim to achieve good ecological and chemical status of European waters by 2015. It has been put in place to aid in protecting and restoring aquatic ecosystems as a basis for ensuring the long term sustainable use of water for people, business and nature.

Recently, the European Commission (EC) launched a policy initiative entitled the “Blueprint to Safeguard Europe’s Waters” to assess the performance of EU water policy and the possibility of achieving the objectives of the WFD by 2020. The blueprint has a time span until 2050 and integrates economic considerations and water quantity and quality objectives. It aims at identifying beneficial strategies towards sustainable water use, while providing a scientific knowledge base and thus aiming to become the new reference of EU water policy for the next two to three decades [6].

Multidisciplinary modeling approaches involving hydrology, ecology, economy, and/or socio-politics have been widely used as tools for the selection of appropriate abatement measures to solve water-related problems [7]. Studies have investigated optimal strategies for conjunctive surface water and groundwater use [8,9]; feedbacks between economic activity and water quality [10]; water pricing and irrigation productivity [11], and water allocation and use between multiple competing sectors [12]. Most of these approaches are either applied locally or consider only one type of objective or measures, leaving a need for a more integrated approach, as attempted in this paper.

Individual or integrated Water Quantity/Quality Models (WQM) may quantify the effectiveness of alternative measures (such as those proposed by Member States in the “Program of Measures” or PoMs in the WFD) to improve water quality and quantity. However, even though WQMs themselves are useful for evaluating single “what-if” scenarios and testing potential management alternatives, they are unable to address the multi-objective problem that involves selecting the most appropriate solutions through a cost-benefit analysis. Selecting the most appropriate combination of management strategies from multiple objectives is difficult and challenging, as solutions require compromises that are acceptable to as many stakeholders as possible.

Selecting the best water strategy (PoMs) from a number of potential alternatives in water resources planning and management is a complex decision making process [13]. It may include conflicting quantitative and qualitative criteria and multiple decision-makers, and can clearly benefit from the use of Multi-Criteria Decision Making (MCDM) techniques [14]. Many applications of Multi-Criteria Analysis (MCA) methods conclude that their main advantage does not lie in providing the ‘answer’, but in endowing such a process with improved transparency; providing a better structuring of the problems; making choices analytically robust, accountable and auditable [15,16,17]; facilitating decision maker learning [18,19,20] and promoting stakeholder involvement [21].

Multi-objective optimization (also known as multi-criteria or Pareto optimization) methods in connection with biophysical models have shown great potential for addressing issues of opposing management goals. Bryan and Crossman [22] developed an optimization-based regional planning approach to identify geographic priorities for ground natural resource management to assess the most cost-effective strategy by optimizing multiple management objectives. Higgins et al. [23] applied a multi-objective integer-programming model, with functions representing biodiversity, water runoff and carbon sequestration. Sadeghi et al. [24] applied an optimization approach to maximize profits from land use, while minimizing erosion risk. Udias et al. [25] and Meyer et al. [26] coupled the model SWAT (Soil and Water Assessment Tool [27]) with an optimization routine to determine optimum farming system patterns to reduce nitrogen leaching while maintaining farmers’ income. Similarly, Whittaker et al. [28] applied SWAT in connection with a Pareto-optimization approach considering profits from land use and chemical pollution from farm production. Udias et al. [29] and Cho et al. [30] coupled Qual2k with a Multi Objective Evolutionary Algorithm (MOEA) to select the adequate treatment type for each wastewater treatment plant to improve water quality at river basin scale.

The aim of our work is develop an integrated multi-criteria hydro-economic modeling framework to provide an overview and diagnoses water status at EU scale and suggest combinations of sustainable measures with respect to water use and water quality. The framework has two main components: the first is an Integrated Water Modeling Platform (IWMP) encompassing four biophysical models and an economic model capable of assessing the implementation of all types of measures included in the PoMs. The biophysical models consist of the land use model LUMP [31], the water quantity model LISFLOOD [32], the crop growth and nutrient cycling and fate model EPIC [27,33], and an integrated water quantity and quality model LISQUAL [6]. The second is a multi-criteria optimization tool for the identification and quantification of the Pareto optimal trade-offs between environmental and economic criteria at EU scale. We aim at providing a set of optimal management options from which stakeholders can identify the most appropriates solutions based on environmental and economic criteria.

The remainder of this paper is organized as follows. In Section 2 we describe the methodology with a particular focus on the integration between the hydrological processes, the PoMs, the optimization procedure and the representation of the decision variables. The last 2 sections present and discuss the main results achieved using the hydro-economic model platform.

2. Methodology

In order to select a set of efficient programs of measures (PoMs) that improve the quality and quantity of water and at the same time are economically sound, we developed an integrated modeling tool (Integrated Water Modeling Platform, IWMP) to assess the effect of each PoM linked to an optimization model to find the Pareto strategies according to the established objectives (multi-criteria analysis). In this section, we describe first the modeling approach and then the details of the components of the multi-criteria analysis.

2.1. Area of Study and Spatial Discretization

To allow a good representation of regional challenges across the continent, Europe was divided into 21 macro regions (Figure 1) based on hydrological and climatological similarities. Performing the modelling exercise based on these 21 regions means less computational requirements (easily parallelized) with more accurate local results.

Major islands (Sicily, Sardinia, and Corsica) were treated as separate regions, as no water transfers take place with the main land. To limit the number of regions, smaller islands were included in continental macro regions. The results section includes examples for the Iberian Mediterranean (region 13) and the Danube (region 11), the first since it is one of the more arid regions in Europe and the second since it is a region, which coincides with a catchment.

The comparison of total water availability to demand was carried out per ‘water region’ (see Figure 1 right), which consist of sub river basins (~5000 km² catchment size) within a country. Based on this, the criteria values for the optimization procedure were calculated for each water region.

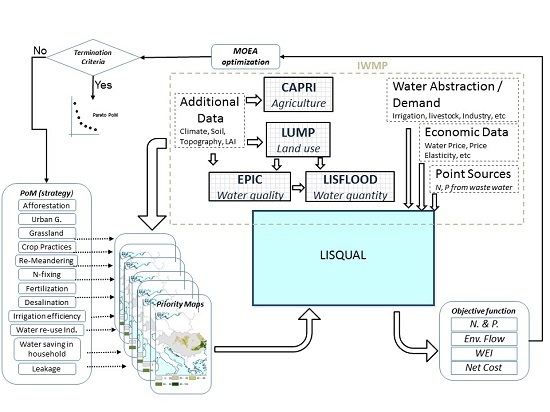
2.2. Integrated Water Modeling Platform (IWMP)

The IWMP is a modeling environment developed to assess the biophysical consequences and costs of combinations of correction measures for Europe. The flowchart in Figure 2 shows how the various models are interlinked, and how the multi-criteria procedure has been designed.

The models used in the platform are described below, including an overview of the main data required for each one.

• CAPRI is an agricultural sector model [34] with a focus on Europe (disaggregation into 280 NUTS2 regions, detailed activity data and coverage of Common Agricultural policies), but embedded in a global market model to represent bilateral trade between 44 trade regions (countries or country aggregates). Its outputs were used to drive the allocation of agricultural land in the LUMP land use model. CAPRI output was used in determining nitrogen and phosphorus fluxes for the EPIC model.
• LUMP is a land use model developed by the JRC to support impact assessment of EC environmental policy [31]. A baseline scenario for the year 2030 was simulated at 100 m resolution, assuming ‘business as usual’ socio-economic trends and consistent with the Common Agricultural Policy (CAP) trends. The 2030 baseline scenario is used together with the 2006 reference land use scenario, which corresponds with the Corine landcover data. LUMP is used to determine the land cover sub-grid information used in the LISFLOOD model.
• EPIC is a crop growth and nutrient cycling and losses model [33] used to calculate nitrogen and phosphorous fluxes from agriculture at pan-European scale, with a 10 × 10 km² grid resolution. EPIC was run with the activated auto-fertilization option where an application of fertilization is performed each time a crop is under nitrogen stress. EPIC was also used to calculate crop water requirements [35].
• LISFLOOD is a spatially distributed (grid-based) hydrological rainfall-runoff and routing model, including a hydrodynamic channel routing routine, developed by the JRC [32,36]. LISFLOOD calculates a complete water balance in daily time steps and for every grid-cell. The meteorological variables driving the LISFLOOD model (precipitation, temperature, wind speed, potential evapotranspiration, and evaporation rates for open water and bare soil surfaces) were derived from various data sources for the period 1 January 1990 until 31 December 2010, including the JRC MARS meteorological database, SYNOP data, as well as data from the European Climate Assessment & Dataset (ECA & D). All meteorological variables were interpolated on a 5 × 5 km² grid. Land use maps of forest, water and sealed (impermeable surface) fractions were derived from LUMP [31] at 100 m resolution. Observed river flow data from 435 gauging stations across Europe were used from the Global Runoff Data Centre (GRDC) for the calibration and validation of LISFLOOD.
• LISQUAL is a bio-physical model that combines water quantity, quality and hydro-economic evaluations. LISQUAL routes the water—if present through hydropower reservoirs and lakes—and for in-stream transformation and transport of N and P [6]. Simulations are made at European scale with a spatial resolution grid of 5 × 5 km²—while including subgrid landuse and elevation related processes at 100 m resolution—and temporal resolution of one day, with for routing a sub-timestep of down to one hour. It is a GIS-based model developed in PCRaster language [37]. LISQUAL uses the surface and subsurface water fluxes from the LISFLOOD output, and the N and P surface and subsurface fluxes from EPIC.

The models interact as follows. The CAPRI model provides the boundary conditions on agriculture to simulate the land use patterns in the LUMP model. LUMP land use model output drives the LISFLOOD model to simulate surface and subsurface water fluxes. CAPRI (fertilizers) and LUMP (landuse) also provide the boundary conditions for EPIC to simulate N and P surface and subsurface fluxes. The EPIC N and P fluxes are then combined with the LISFLOOD water fluxes to perform the integrated simulations with LISQUAL [38], which then yields river water quality estimates and water scarcity and flood indicators. LISQUAL also includes water abstractions and point sources discharge of water and pollutants (e.g., waste water treatment plants). LISQUAL also calculates the total costs of specific abatement measures applied, as well as cost-estimates of damages for various sectors: flood damage, yield loss costs, industrial production loss costs, household welfare loss due to water scarcity.

Water withdrawals were calculated for the baselines 2006 and 2030 for the public, industrial, energy, and agricultural (irrigation and livestock) sectors. Withdrawals for the first three sectors were based on sectoral water use statistics derived from the OECD/EUROSTAT Joint Questionnaire on Inland Water and AQUASTAT-FAO. The disaggregation of this country-level data was done to the relevant land use classes for the reference year 2006, and extrapolated to 2030 using the simulated land use and driving factors (i.e., population density, industrial GVA and energy consumption). This methodology is further described in [39]. Based on crop growth, soil water and the EPIC nutrient model, irrigation water requirements [40] were estimated on a daily basis at a 10 × 10 km² grid scale. Daily maps of livestock water withdrawal [41] were calculated using the Food and Agriculture Organization (FAO) livestock density maps and output from the CAPRI agricultural model [34,42]. Point source pollution data for EU27was retrieved from the UWWTP (Urban Waste-Water Treatment Plants) database published by the European Environment Agency (EEA). A full description of the models, data inputs (dams operating rules, etc.) and their integration is given in [6].

2.3. Scenarios

Two baseline scenarios were used as references to compare the effect of each PoM. The baseline 2006 represents the current socio-economic and environmental situation (status quo) and is implemented using the CORINE Land Cover 2006 map [43] and current water demand for the domestic, agricultural, industry and energy sectors.

The differences between the baseline 2006 and baseline 2030 are due to changes in land-use, causing, for example, different evapotranspiration and infiltration response, and changes in sectoral water demand.

Individual mitigation measures were simulated next, and were thus pre-processed within EPIC and LISFLOOD. Therefore, for example, the urban greening measures was simulated in all cities fulfilling the criteria, and changes in the pixel fluxes of water, N and P were calculated, as well as the costs of the individual scenario per pixel.

A combination of measures scenario is then accumulating these changes in water, N, and P fluxes and costs, and routing those within the LISQUAL model. Certain measures are as such only implemented in the most promising areas, which is where they have the most significant impact on the water, N and P fluxes.

2.4. Multi Criteria Analysis (Optimal Program of Measures Selection)

A multi-criteria analysis was performed to select the most efficient PoMs (combination of measures) for each European region. The analysis was based on the combination of the previously described Integrative Water Modeling Platform (IWMP) with a multi-criteria optimization algorithm (MOEA, Figure 2).

2.4.1. Measures Considered

The abatement measures considered are based on a previously completed a study on natural water retention, water saving, and nutrient reduction measures, identifying their potential impacts on EU water policy, both in economic and environmental terms [44,45]. This assessment brings together different possible land-use and socio-economic scenarios and looks at their implications for water resource availability.

Table 1. Short description of the measures considered in the Blueprint. Group on each measure is included according to the type of effect that is expected to produce.

Measure	Group	Description of the Measure
Afforestation	Flooding	Focused to increase forest areas (reforestation above 500 m altitude, with slope >10%) using the LUMP model.
Urban greening	Flooding Water saving	Combination of abatement measures aimed at increasing the green infrastructure (e.g., green roofs, rain gardens, parks, flowerbeds) in urban areas by up to 25% of the current amount.
Grassland	Flooding	Combination of abatement measures to increase the cultivated areas and pasture by 10%, restricted to slopes larger than 10% using the LUMP model.
Crop Practices	Flooding Agriculture	Simulates the implementation of improved crop practices (increase organic matter; use of mulching and zero-tillage; increase of soil infiltration).
Re-Meandering	Flooding	Increases the meandering of the current (small to medium) rivers; i.e., increasing the length and storage capacity of the river bed.
N-fixing and Optimum Fertilization	Agriculture	Reduction of nitrate and phosphate concentrations, mostly in agriculture drainage and runoff through optimal fertilizer management including the use of nitrogen fixing crops.
Desalination	Water saving	Desalinization plants along the coastlines for each European region are assumed to treat 60 Mega-liters of water per day, which is used within 150 km of the plant.
Irrigation efficiency	Agriculture Water saving	This measure assumes an improvement in irrigation efficiency from the current averages (74% for Eastern, and 77% for Western Europe) to 93%, by applying drip irrigation everywhere.
Water re-use in industry	Agriculture Water saving	It assumes that 50% of the water abstracted for industry is re-used in the production cycle.
Water saving in household	Water saving	This assumes 25% of water savings in the domestic sector, adopting simplistic measures (e.g., replacing showerheads, using softener, etc.).
Leakage	Water saving	Assumes a reduction in the current leakage in public water of 50%.

gives a short description of all measures involved in the simulations. The group column in Table 1 refers to the type of sector or effect on which each measure has significant influence. Some of the measures are in more than one group because they affect to more than one sector. The groups of effects considered here include: flooding, water saving and agricultural. The group of flooding measures aims to reduce flood risk by increasing water retention. The group of agricultural measures includes promoting better crop practices in agriculture, e.g., nutrient reduction and mulching. The water savings group of measures aims to reduce urban and industrial water use.

2.4.2. Criteria Considered

For this framework four environmental related objectives and one economic objective were considered in the optimization process:

• Minimize Nitrate (N) and Phosphate (P) concentrations in surface water: Nitrogen and phosphorous concentrations are two criteria that describe the water quality status. These nutrients when in excess can harm the environment. Higher concentrations are due human activities. Phosphorus is mostly discharged through wastewater treatment plants (point sources), while nitrates are mostly linked to agricultural activity (diffuse sources).
• Minimize the number of days during which Environmental Flow is below the reference (Env10Flow): This criterion is related to water scarcity and drought, evaluating the number of days below a certain reference quantity flow. It could be considered as the environmental flow required to achieve Good Ecological Status. It is based on a threshold calculated for current rivers, but without the current water abstraction and consumption using model simulations of the baseline 2006 scenario for a period of 30 years. We compute it by calculating the 10th percentile of daily river discharge at each location on a monthly basis (Env10Flow). For the Baseline 2030 and for each scenario measure, the days below the 10th percentile are counted. The environmental flow criterion is calculated for each single river pixel for a period of 30 years and spatially aggregated for the catchment area.
• Minimize Water Exploitation Index (WEI): This is an index that takes into account the level of use of the water. It is calculated along the lines of the Water Scarcity and Drought Expert Group, based on the water balance equation for each water region:

  $$\text{WEIabs}=\frac{\text{total abstraction}}{\text{External inflow}+\text{internal flow}}$$

  (1)

  where:

  • Internal flow = net generated water (rainfall − evapotranspiration + snowmelt);
  • External inflow: inflow from upstream areas.
  The index is calculated for the entire simulation period of 30 years. The value of the criterion is computed by the 90% quantile of annual WEI_abs (WEI abstraction) of a period of 30 years is calculated and only WEI_abs greater equal 0.5 is taken into account for calculating the spatial average. The aim of the simulations, run in this job, is to optimize for a lower WEI_90% level.
• Minimize the Net Cost Value: In this objective we consider the cost of the measures and the monetary values of sectorial water uses, and the final value is computed according with Equation (2). Each cost component has been calculated by multiplying the area of the applied scenario with the costs per hectare of the scenario, corrected with the comparative price level per country (Equation (2)).

  $$\begin{array}{l}{\text{Net Cost Value}}_{\text{PoM}}={\displaystyle {\displaystyle \sum }_p}[{\text{ICost}}_{\text{PoM}}(\mathrm{p})*\text{AI}(\mathrm{p})\\ +{\text{MCost}}_{\text{PoM}}(\mathrm{p})*\text{AM}(\mathrm{p})+{\displaystyle {\displaystyle \sum }_{\mathrm{s}}}[[{\text{WUV}}_{\text{BLS}}(\mathrm{s},\mathrm{p})-{\text{WUV}}_{\text{PoM}}(\mathrm{s},\mathrm{p})]*\text{AU}(\mathrm{s},\mathrm{p})]]\end{array}$$

  (2)

  where:

  • ICost_POM(p): Cost of implementing of the PoM per unit of area in pixel p;
  • AI(p): Area in pixel p were PoM are implementation cost.
  • MCost_POM(p): Cost of maintenance of the PoM per unit of area in pixel p;
  • AM(p): Area in pixel p were PoM are maintenance cost.
  • WUV_POM(s,p): Water use economic value for PoM in sector s, per unit of area in pixel p;
  • AU(s,p): Area in pixel p were water use in sector s has a value.
  • WUV_BLS(s,p): Water use economic value for Baseline in sector s, per unit of area in pixel p.

To evaluate the cost of the measures (except for desalination) we considered the: cost of investment per unit (€/ha) related to e.g., construction, acquisition and compensation of land requirement; and operation and maintenance cost per unit (€/ha/year). For the desalination measure we considered the cost per m³, the distance to the desalination plant, and the altitude difference between the point of usage and the plant. The water retention improvement measures require a specific cost evaluation in their applications (as investment unit). For the simulations the cost for each natural water retention measure was estimated using the studies of Stella Consulting [44] and Burek et al. [45].

The water use by sectors in which the values are computed are: industry-manufacturing, domestic, agricultural, energy production sector and for the expected flood damage of one 100 years’ flood. The absolute value of this economic values are summed up for the considered area and for the period of time (30 years); then they are displayed as cost of €1000 per km². It should be noted that some scenarios may end up with negative costs, meaning that the benefits—i.e., reduced flood damage, reduced economic losses—are larger than the cost of investment and maintenance of the correction measures.

For all the criteria the criteria calculation is performed through modelling on a 5 × 5 km² grid using the weather of 1990–2010. The final result for each criterion is generated by summing the values of each pixel on the analyzed region. Consequently, for each region and criterion the obtained result was a single numerical value. The indicator of flooding events was assessed using the calculated 50 and 100 years return period river discharge. In addition, this indicator allows the evaluation of the economic losses also for the water scarcity in the different sectors such as agriculture, industry, domestic and public use, etc. In the same way a 100 years return period for potential flood damage was evaluated.

2.4.3. Priority Maps

For each measure, a priority map is defined, with values for each pixel ranging from 0% to 100% (Figure 3), in order to rank the priority of selection of this kind of measure in each pixel. The priority map represents the areas where it is possible to apply a type of measure and, within these, the higher priority represents zones where its application is more efficient. If a type of measure is applied with an intensity of 100%, this measure is used in all pixels of the map (actually in all the pixels where is possible to apply this measure). However, if a measure is applied with an intensity of 5% only at those points with an efficiency larger than 95% (darker green color dots on the map in Figure 3 left) will be selected. A pixel with a higher priority has a higher chance to be selected, i.e., a pixel with a priority of 80% is selected if the level of intensity with which the measure is applied is between 20% and 100% while a pixel with priority 10% is only selected if the measures application intensity is between 90% and 100%. Figure 3 (right/top) shows the area which is selected if the type of measures intensity is 50%, (right/bottom) shows a bigger area if the scenario intensity is 75%.

The priority map for each type of measure is calculated based on the appropriate local information (soil, climate, land use, population, water use, etc., in the region). Within the IWMP, for one region, all the priority maps (one for each measure) are generated before starting the optimization process. In this preprocess stage the priority maps are generated from different models: LISFLOOD EPIC (Figure 2).

2.4.4. Optimization Algorithm

Optimization in the methodological approach leads to a reduction of the value of a criterion in response to the PoM applied. That is, the intensity of application of the considered restoration measures. Gradient based approaches are not the most suitable to solve our optimization problem, since they present some difficulties such as non-convexity, lack of knowledge of ranges of fitness functions, and non-differentiability of the landscape [46]. In fact, gradient-free methods such as evolutionary algorithms [47] are increasing in their number of applications in recent years due to their flexibility in dealing with these issues. In addition, Multi Objective Evolutionary Algorithms (MOEAs) are relatively robust and efficient in solving multi criteria problems, and do not require the decision maker to carry out an a priori articulation of preferences [48]. Details on different algorithms, which implement a specific MOEA are discussed in Deb et al. [49].

For these reasons, a MOEA optimizer was used to find the Pareto PoM (strategies), based on that presented in Udias et al. [29]. The MOEA encodes the PoM to be optimized in a chromosome. Thus, each chromosome (optimization string) is a fixed-length array of real values [47] each of which represents the intensity level of application of one specific type of measures from those described in Table 1 (see Figure 4). Therefore, depending of the group of measures considered in the optimization process (

Table 2. Overview of the three groups of abatement measures used in the preliminary optimization exercise. The groups are defined according to the type of sector or effect on which each measure has significant influence.

Flooding	Agriculture	Water Saving
Afforestation	Crop practices	Urban greening
Urban greening	Nitrogen fixing	Desalination
Grassland	Optimum fertilization	Irrigation efficiency
Crop practices	Irrigation efficiency	Water reuse in industry
Re-Meander	Water reuse in industry	Water saving household
		Leakage reduction

), the genes represent one different set of measures.

A number of individuals (chromosomes) form a population. The MOEA repeats the evaluation process for all the strategies (chromosomes) of the population. Further, solutions are selected for mating, according to their fitness to form new solutions, that is, offspring. The mating is performed in this implementation by means of tournament selection, Gaussian mutation and arithmetical crossover operator to generate the new population [50]. The algorithm also introduces elitism by maintaining an external population. In each generation, the new solutions belonging to the internal population are copied to the external population when they are not Pareto-dominated by any solution for this external population. If solutions for the external population are dominated by some of the new solutions, these solutions are deleted from the external population. The external elitist population is simultaneously maintained in order to preserve the best solutions found so far and to incorporate part of the information in the main population by means of the crossover. Elitism is also included in this recombination process, selecting each of the parents through a fight (tournament), between two randomly-selected chromosomes from the external Pareto set (according to a density criterion) or from the population set (according to their ranking determined through a dominance criterion). This process is continually repeated for a given number of iterations know as generations or until the convergence conditions are satisfied.

Combining the intensity of application of each measure (form each chromosome values) with their corresponding priority maps, the IWMP generates a simulation scenario for each chromosome solution. Then, this scenario is evaluated by the LISQUAL model. For each measure, its priority map and application level (the corresponding value in the chromosome proposed by the MOEA) defines which pixels are active and which not for this family of measures. Finally, with this scenario the IWMP calculates the final value of all the criteria considered. The IWMP repeats this fitness evaluation for all the chromosomes (PoM) of one population, and this information is used by the MOEA to generate the next generation population. After some generations the optimization algorithm reaches convergence. The output of the optimization process is a set of chromosomes, corresponding with non-dominated strategies (PoM) known as Pareto-optimal solutions [49] (Deb et al., 2001) that can be visualized in a two or more dimensional plot to see the trade-off solutions between the different objective functions. For each individual on that front, any one objective cannot be improved without losing of the other objectives, see Figure 5.

The first generation strategies (intensity of each type of measures) of the optimization process are generated randomly. When prior information is available, the optimization process converges faster if the initial strategies (chromosomes) are generated with this information instead of randomly. Expert knowledge could be used or the Pareto set obtained in previous executions of the same or other regions.

2.5. Software and Harware Requiremetns

The process of generation and evaluation of each scenario was computationally expensive. Depending on the size of the region, between 10 and 50 min were needed to execute each evaluation of the IWMP, with an Intel Xeon 2.40 GHz CPU, 16 Gb of RAM memory and solid-state drive OCZ-Vertex3 hard disk. Therefore, the number of evaluations (computational iterations), which allowed the proper definition properly of the Pareto front, should be as small as possible. In the end a time interval of almost 2–10 days was needed for the whole optimization procedure.

Different computational and software resources were used in the execution of these simulations. The software language Python was used as integration platform for all the models, in this way all the flow data was managed in Python. Python was also used in the execution of the iterative procedure to assess the optimization process.

The software for environmental modeling PCRaster (developed by Utrecht University) was used for the analysis of the time series maps used for the main raster GIS operations. PCRaster is a raster-based system; its architecture permits the integration of environmental modeling functions with classical GIS operations.

The R programming language for statistical analysis (integrated with GDAL functions) was used to develop a script able to make the calculation of the 50 and 100 years return period river discharge.

3. Results and Discussion

Since the main objective of this paper is to present the integrative multi criteria methodology and its potential to aid in decision-making at European level, we only present preliminary examples of how the methodology was applied to the Danube and the Iberian Mediterranean regions.

For computational and practical reasons, instead of execute studies considering simultaneously the application of all the types of correction measures (the 11 described in Table 1), in this optimization exercise we make executions by each one of the groups of measures defined in Table 1, and summarized in Table 2.

The multi-criteria optimization procedure was performed in an independent way for each region and each of these groups of measures (strategies). The MOEA’s decision variables are the level of intensity with which the type of measure is applied (Figure 4). The strategies contained five variables in the flooding and agriculture case and six in the water saving case (Table 2). For each application level (proposed by the MOEA), the IWMP firstly generates the corresponding priority map, then a scenario combining all the measures priority maps. Finally, the models are run with the combined scenario in order to estimate the effect (value of the criteria) of the application of the strategy or combined scenario.

We considered that the convergence was reached when a set of near Pareto frontier strategies was found close enough to the optimal set (within 5% of the true Pareto frontier). This approximation should be adequate considering that the results are to be used as general guidelines in the decision making process (rather than accurate prediction), and furthermore that the uncertainty associated with the data and the models used it is not negligible. This vicinity to convergence point is achieved in a few hundred evaluations of the objective function (performed by the IWMP) with a fine tuning setup of the MOEA parameters (crossover and mutation operator rates), small population size (10 chromosomes per generation) and starting the optimization process with the best strategies identified in previous executions (instead of generating random strategies).

Table 3. Overview of the group of main criteria considered for optimization.

Flooding	Agriculture	Water Saving
Economic Value	Economic Value	Economic Value
Environmental Flow	Environmental Flow	Environmental Flow
Cost Flood	N	N
WEI	WEI	WEI

shows the objectives considered simultaneously for each group of measures during the optimization process.

In some cases two of the considered objectives evolve in the same direction under the effect of the measures considered. For example, Figure 6 shows the simultaneous improvement of the values of the WEI and environmental flow objectives for the water saving strategy for the Danube and Iberian Peninsula regions. The N and P objectives also evolve in the same direction in most cases. Figure 6 shows how even for objectives that evolve in parallel, the results give us valuable information about the compromise between these objectives and the range of values taken.

In Figure 6, Figure 7 and Figure 8 the strategies corresponding to the 2030 baseline situation can be identified by a red point. It can be seen in Figure 6A,B that the baseline 2030 strategy is undesirable, since the best strategy would be the one situated at the bottom left corner of the figures.

The outputs of the near Pareto frontier strategies between conflicting objectives generated by the tool are especially useful for managers and stakeholders to take decisions selecting from a few efficient (Pareto optimal) strategies, according to the considered criteria. The Pareto curves between criteria slope also reveal the degradation rate of an objective to achieve one unit of improvement in a conflicting objective. This is also valuable information for the negotiation process before the final strategy choice.

Figure 7 illustrates the results for the optimization run of the agriculture related measures group (strategies S1 to S8 in

Table 4. Pareto PoMs obtained for the N, WEI and Environmental flow criteria for the Danube catchment, considering the agriculture related correction measures (CR: crop practices, NIF: N fixing, OF: optimum fertilization, IR: irrigation efficiency, RE: water reuse in industry).

Strategy	Type of Measures Intensity					Criteria
	CR	NIF	OF	IR	RE	Env. Flow	N	WEI
S1	0.00	0.00	0.00	1.00	0.00	151.21	1.74	1.06
S2	0.00	0.38	1.00	0.99	0.98	151.73	1.02	1.07
S3	0.14	0.73	1.00	0.99	0.99	154.30	0.89	1.08
S4	0.14	0.79	1.00	1.00	1.00	154.48	0.84	1.07
S5	0.32	0.91	0.81	0.98	1.00	157.12	0.76	1.10
S6	0.29	0.94	0.99	0.99	0.13	157.61	0.61	1.11
S7	0.29	0.95	1.00	1.00	0.13	157.65	0.60	1.11
S8	0.00	0.99	1.00	1.00	0.85	159.06	0.56	1.11

) in the Danube region. The red line represents the Pareto frontier according to the two environmental objectives N and environmental flow. It can be seen that in strategy S2 (given in Table 4) the nitrate concentration is much lower than in S1 (1.74 to 1.00 mg/L), with hardly any deterioration in the environmental flow criterion. Both strategies are Pareto efficient, but it would not be appropriate for a decision maker to choose the S1 strategy since it would result in only a small improvement in the environmental flow criteria, paired with a much greater degradation in the water quality (higher N value).

Each point in the objectives space (Figure 7) corresponds to another point in the decision space (management strategies). For example, for agriculture related strategies, the decision space has five variables (Table 2), each one representing the implementation rate for one family of abatement measures.

Table 4 shows the values of these five decision variables (improvement measures rates) for all the Pareto strategies marked on the red line in Figure 7, including also the values obtained for the three objectives. As shown in Figure 7, when the N quality improves, environmental flow deteriorates and vice versa. The WEI does not seem to vary much within the agricultural measures group, and its improvement is in the same direction as the environmental flow.

Figure 9 and Figure 10 show the spatial allocation of each type of PoM in the Danube region. The measure applied in each zone was determined by the previously defined priority maps (note that 100% of applications of one PoM do not need to match with the whole region) and the value of the decision variables in the strategy. Figure 9 compare the S1 (Figure 9A) and S8 (Figure 9B) strategies from Table 4. Although the crop related abatement measures are applied to some extent in some of the Pareto front strategies (Table 4), the mapped strategies do not apply it at all. On the other hand, all efficient strategies apply the irrigation (IR) related measures to its maximum rate. As expected, the measures of nitrogen fixation (NIF) have a major influence on the value of the N concentration criterion, and when the optimizing fertilization (OF) measures are not applied the highest concentration of N occurs.

Figure 8 compares the environmental flow and flooding cost objectives of the strategies coming from an optimization process for the flooding group of measures in the Danube and the Mediterranean Iberian Peninsula regions respectively. As in Figure 7, red dots represent the baseline 2030 situation. It is interesting that, in both cases, this strategy belongs to the Pareto set, even though it is associated with a high cost of flooding. In addition, notable is that the cost of flooding is four times higher in the Danube region than in the Iberian Peninsula.

As pointed out in the methodology section, the economic criterion is taken into account. However, since the considered costs are still under validation, the results discussed here only include the component of the cost function related to floods (Figure 8).

Table 5. Pareto PoM obtained according to N, WEI and Environmental flow criteria for the Danube catchment considering the flooding-related family of abatement measures (AF: afforestation, UG: urban greening, GR: grassland, CR: crop practices, ME: re-meander). Cost flood in 1000 €/km².

Strategy	Type of Measures Intensity					Criteria
	AF	UG	GR	CR	ME	Env. Flow	Cost. Flood	N	WEI
S1	0	0	0	0	0	153.81	46.71	1.76	1.20
S2	0.32	0	0	0	0.74	153.87	44.63	1.74	1.20
S3	0.11	0.99	0	0.03	0.85	154.26	42.72	1.72	1.20
S4	0	0	0	0	1	154.92	41.98	1.64	1.20
S5	0.84	0.18	0	0.78	1	155.01	41.71	1.65	1.20
S6	0.98	1	0	0.61	1	155.42	40.49	1.65	1.21
S7	1	1	0	0	1	155.49	40.29	1.64	1.21
S8	0.63	0.96	0.47	0.44	0.9	156.87	40.05	1.69	1.23
S9	0.92	0.26	0.61	0.62	1	157.79	38.60	1.64	1.24
S10	1	1	0.64	0	1	158.25	37.40	1.63	1.25

and

Table 6. Pareto PoM obtained according to N and Environmental flow criteria for the Iberian Peninsula region considering the flooding related family of correction measures (AF: afforestation, UG: urban greening, GR: grassland, CR: crop practices, ME: re-meander). Cost flood in 1000 €/km².

Strategy	Type of Measures Intensity					Criteria
	AF	UG	GR	CR	ME	Env. Flow	Cost. Flood	N	WEI
S1	0	0	1	0	0	178.14	11.59	0.53	0.95
S2	0.81	0.03	0.83	0	0.34	178.54	11.05	0.54	0.96
S3	0.65	0.13	0.14	0.3	0.74	178.96	10.06	0.53	0.97
S4	0.86	0.14	0.44	0.52	0.65	179.19	9.80	0.53	0.97
S5	0.48	0.93	0.11	0.99	0.45	179.45	9.27	0.53	0.98
S6	0.68	0.69	0.16	0.85	0.99	180.32	9.00	0.5	0.97
S7	0.95	0.56	0.05	0.79	0.97	180.79	8.87	0.5	0.97
S8	1	0	0	1	1	181.18	8.74	0.5	0.98

show the value of the decision variables (water improvement rates) for some of the Pareto frontier strategies (red line) from Figure 8 as well as the outcomes of four objectives.

For the Danube region, none of the Pareto frontier strategies (Figure 8A, Table 5) had much effect on the WEI objective (only very small improvements in the same direction as the environmental flow). Nitrates also showed only slight improvements for these strategies.

A comparison of the baseline scenario (S1 strategy) with the S10 strategy (Table 5) is shown in Figure 10. From the Pareto set solution, the S1 strategy (no improvement measures applied) leads to higher flood costs but the best environmental flows. On the other hand, strategy S10 applies afforestation, urban greening and re-meandering to all areas in which it can be applied, the grassland measure (GR) in more than half of the areas, but no crop practices (CR). Figure 10 shows how the S10 strategy applies measures even simultaneously throughout most of the Danube Region.

Concerning the comparison between the regions (Table 5 and Table 6), the environmental flow quality is better in the Danube, whilst both the WEI and N are far better in the Iberian Peninsula. Regarding the decision variables, in the Iberian Peninsula region we note that the reduction in the cost of flooding (and consequently the increase in environmental flow) is produced by increasing the measures related with crop practices (CR) and re-meandering (ME), and by decreasing the grassland (GR) measures. For the Danube, the meandering measures seem to have a similar behavior, but the grassland have an opposite behavior to that of the Iberian Peninsula.

4. Conclusions and Limitations of the Approach

In the framework of policy initiatives such as the EU “Blueprint to safeguard Europe’s waters”, there is a need to develop methods to be able to select favorable measures, which simultaneously meet multiple criteria.

Most existing projects have suggested partial approaches that examine only a single measure at local scale (catchment level). We propose an integrative multi criteria methodological tool assessing combinations of measures in river basins, bringing together land-use and socio-economic scenarios and looking at the implication for multiple water resources indicators, such as quantity, quality and their extremes. Climate projections can also be taken into account, but have not been considered here since we wanted to look at a relative short time horizon of 2030, and isolate the effect of the measures. The methodological tool integrates several biophysical models (CAPRI, LUMP, LISFLOOD, EPIC and LISQUAL) with a hydro-economic model under a multi criteria perspective. Using this tool, efficient trade-off strategies can be found which consider the applications of different types of environmental improvement measures simultaneously.

With this approach, we seek to maximize the net social benefits of the use of water by economic sectors, including a range of components, such as welfare impacts for water users, valuation of key ecosystem services provision, valuation of external costs from degradation of ecological and chemical status and energy consumption triggered by water abstraction and return.

For some countries, preliminary simulations have been carried out to assess the effects of water retention measures, water savings measures, and nutrient reduction measures on several hydro-chemical criteria. These preliminary simulations show that the IWMP can deliver near Pareto frontier strategies.

This EU-wide integrated model aims at ex-ante evaluations at European level, to evaluate policy options towards a green economy and funding instruments. However, it should be noted that the underlying data made available by the EU countries (through Eurostat, the European Soils Bureau, CORINE, GRDC and several bilateral data agreements) have their own limitations and uncertainties, and that the current model results should therefore only be interpreted as a first comparison between territories. Anticipating the envisaged application of the modeling platform to support the impact assessment of sectoral policies and evaluate River Basin Management Plans (RBMP), several improvements are currently being implemented. In any case, the tool could be very helpful to provide transparency in the selection of abatement measures by the stakeholders or provide alternative solutions.

The study shows that this modeling software environment can technically deliver efficient scenario combinations that improve various water quantity and quality indicators, but that additional work is needed before policy advice can be made using the tool. Especially the economic loss estimations, the data on water prices and price-elasticity, as well as the implementation and maintenance costs of individual correction measures need further work.

Additional limitations:

• The price of water used in this study was that of the public sector, due to a lack of complete data from the other sectors. The price of water for agriculture and industry is in many cases lower than the public price; economic losses for especially industry may be overestimated this way.
• Lack of data quantifying large-scale water transfers across river basin borders.
• Further work using uncertainty of the data and assumptions used should be performed in order to use assess its influence on the measures selection process.