Behavior of Floquet Topological Quantum States in Optically Driven Semiconductors
Abstract
:1. Introduction
2. Quantum Many Body Theory for Correlated Electrons in the Non-Equilibrium
2.1. Floquet States: Coupling of a Classical Driving Field to a Quantum Dynamical System
2.2. Dynamical Mean Field Theory in the Non-Equilibrium
3. Floquet Spectra of Driven Semiconductors
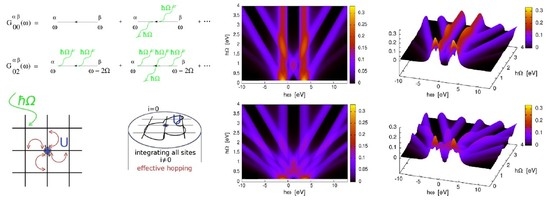
3.1. Development and Lifetimes of Floquet Topological Quantum States in the Non-Equilibrium
3.2. Topological Generation of Higher Harmonics and of Optical Transparency
3.3. Consistency of the Numerical Framework
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kosterlitz, J.M.; Thouless, D.J. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C Solid State Phys. 1973, 6, 1181. [Google Scholar] [CrossRef]
- Fu, L.; Kane, C.L.; Mele, E.J. Topological Insulators in Three Dimensions. Phys. Rev. Lett. 2007, 98, 106803. [Google Scholar] [CrossRef] [Green Version]
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045. [Google Scholar] [CrossRef]
- Fu, L.; Kane, C.L. Superconducting Proximity Effect and Majorana Fermions at the Surface of a Topological Insulator. Phys. Rev. Lett. 2008, 100, 096407. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moore, G.; Read, N. Nonabelions in the fractional quantum hall effect. Nucl. Phys. B 1991, 360, 362. [Google Scholar] [CrossRef]
- Goldmann, N.; Dalibard, J. Periodically Driven Quantum Systems: Effective Hamiltonians and Engineered Gauge Fields. Phys. Rev. X 2014, 4, 031027. [Google Scholar] [CrossRef] [Green Version]
- Zutic, I.; Fabian, J.; Das Sarma, S. Spintronics: Fundamentals and applications. Rev. Mod. Phys. 2004, 76, 323. [Google Scholar] [CrossRef]
- Nayak, C.; Simon, S.H.; Stern, A.; Freedman, M.; Das Sarma, S. Non-Abelian anyons and topological quantum computation. Rev. Mod. Phys. 2008, 80, 1083. [Google Scholar] [CrossRef]
- Rechtsman, M.C.; Zeuner, J.M.; Plotnik, Y.; Lumer, Y.; Podolsky, D.; Dreisow, F.; Nolte, S.; Segev, M.; Szameit, A. Photonic Floquet topological insulators. Nature 2013, 496, 196. [Google Scholar] [CrossRef]
- Bandres, M.A.; Wittek, S.; Harari, G.; Parto, M.; Ren, J.; Segev, M.; Christodoulides, D.N.; Khajavikhan, M. Topological insulator laser: Experiments. Science 2018, 359. [Google Scholar] [CrossRef]
- Lubatsch, A.; Frank, R. A Self-Consistent Quantum Field Theory for Random Lasing. Appl. Sci. 2019, 9, 2477. [Google Scholar] [CrossRef]
- Bernevig, B.A.; Hughes, T.L.; Zhang, S.-C. Quantum Spin Hall Effect and Topological Phase Transition in HgTe Quantum Wells. Science 2006, 314, 1757. [Google Scholar] [CrossRef] [PubMed]
- König, M.; Wiedmann, S.; Brüne, C.; Roth, A.; Buhmann, H.; Molenkamp, L.W.; Qi, X.-L.; Zhang, S.-C. Quantum spin hall insulator state in HgTe quantum wells. Science 2007, 318, 766. [Google Scholar] [CrossRef] [PubMed]
- Hsieh, D.; Qian, D.; Wray, L.; Xia, Y.; Hor, Y.S.; Cava, R.J.; Hasan, M.Z. A topological Dirac insulator in a quantum spin Hall phase: Experimental observation of first strong topological insulator. Nature 2008, 452, 970–974. [Google Scholar] [CrossRef] [PubMed]
- Xia, Y.; Qian, D.; Hsieh, D.; Wray, L.; Pal, A.; Lin, H.; Bansil, A.; Grauer, D.; Hor, Y.S.; Cava, R.J.; et al. Discovery (theoretical prediction and experimental observation) of a large-gap topological-insulator class with spin-polarized single-Dirac-cone on the surface. Nat. Phys. 2009, 5, 398. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, C.-X.; Qi, X.-L.; Dai, X.; Fang, Z.; Zhang, S.-C. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 2009, 5, 438–442. [Google Scholar] [CrossRef]
- Lindner, N.H.; Refael, G.; Galitski, V. Floquet Topological Insulator in Semiconductor Quantum Wells. Nat. Phys. 2011, 7, 490–495. [Google Scholar] [CrossRef]
- Katan, Y.T.; Podolsky, D. Modulated Floquet Topological Insulators. Phys. Rev. Lett. 2013, 110, 016802. [Google Scholar] [CrossRef] [Green Version]
- Rudner, M.S.; Lindner, N.H.; Berg, E.; Levin, M. Anomalous Edge States and the Bulk-Edge Correspondence for Periodically Driven Two-Dimensional Systems. Phys. Rev. X 2013, 3, 031005. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Wang, B. Effects of light on quantum phases and topological properties of two-dimensional Metal-organic frameworks. Sci. Rep. 2016, 4, 41644. [Google Scholar] [CrossRef]
- Kitagawa, T.; Oka, T.; Brataas, A.; Fu, L.; Demler, E. Transport properties of nonequilibrium systems under the application of light: Photoinduced quantum Hall insulators without Landau levels. Phys. Rev. B 2011, 84, 235108. [Google Scholar] [CrossRef] [Green Version]
- Gu, Z.; Fertig, H.A.; Arovas, D.P.; Auerbach, A. Floquet Spectrum and Transport through an Irradiated Graphene Ribbon. Phys. Rev. Lett. 2011, 107, 216601. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.H.; Steinberg, H.; Jarillo-Herrero, P.; Gedik, N. Observation of Floquet-Bloch States on the Surface of a Topological Insulator. Science 2013, 342, 453–457. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lindner, N.H.; Bergman, D.L.; Refael, G.; Galitski, V. Topological Floquet spectrum in three dimensions via a two-photon resonance. Phys. Rev. B 2013, 87, 235131. [Google Scholar] [CrossRef]
- Jiang, L.; Kitagawa, T.; Alicea, J.; Akhmerov, A.R.; Pekker, D.; Refael, G.; Cirac, J.I.; Demler, E.; Lukin, M.D.; Zoller, P. Majorana Fermions in Equilibrium and in Driven Cold-Atom Quantum Wires. Phys. Rev. Lett. 2011, 106, 220402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- D’Alessio, L. Rigol, Dynamical preparation of Floquet Chern insulators. Nat. Commun. 2015, 6, 8336. [Google Scholar] [CrossRef]
- Grushin, A.G.; Gomez-Leon, A.; Neupert, T. Floquet Fractional Chern Insulators. Phys. Rev. Lett. 2014, 112, 156801. [Google Scholar] [CrossRef] [Green Version]
- Bergholtz, E.; Liu, Z. Topological Flat Band Models and Fractional Chern Insulators. Int. J. Mod. Phys. B 2013, 27, 1330017. [Google Scholar] [CrossRef]
- Floquet, G. Sur les équations différentielles linéaires à coefficients périodiques. Ann. l’ Ecole Norm. Sup. 1883, 12, 47–88. [Google Scholar] [CrossRef]
- Razavi-Khosroshahi, H.; Edalati, K.; Wu, J.; Nakashima, Y.; Arita, M.; Ikoma, Y.; Sadakiyo, M.; Inagaki, Y.; Staykov, A.; Yamauchi, M.; et al. High-pressure zinc oxide phase as visible-light-active photocatalyst with narrow band gap. J. Mater. Chem. A 2017, 5, 20298–20303. [Google Scholar] [CrossRef]
- Fritsch, D.; Schmidt, H.; Grundmann, M. Pseudopotential band structures of rocksalt MgO, ZnO, and Mg 1 x Zn x O. Appl. Phys. Lett. 2006, 88, 134104. [Google Scholar] [CrossRef]
- Dixit, H.; Saniz, R.; Lamoen, D.; Partoens, B. The quasiparticle band structure of zincblende and rocksalt ZnO. J. Phys. Condens. Matter 2010, 22, 125505. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, F.; Lin, Z.; Lin, W.; Zhang, J.; Ding, K.; Wang, Y.; Zheng, Q.; Zhan, Z.; Yan, F.; Chen, D.; et al. Research progress in ZnO single-crystal: Growth, scientific understanding, and device applications. Chin. Sci. Bull. 2014, 59, 1235–1250. [Google Scholar] [CrossRef]
- Park, W.I.; Jun, Y.H.; Jung, S.W.; Yi, G.-C. Exciton emissions observed in ZnO single crystal nanorods. Appl. Phys. Lett. 2003, 82, 964–966. [Google Scholar] [CrossRef]
- Faisal, F.H.M.; Kaminski, J.Z. Floquet-Bloch theory of high-harmonic generation in periodic structures. Phys. Rev. A 1997, 56, 748. [Google Scholar] [CrossRef]
- Lubatsch, A.; Frank, R. Evolution of Floquet topological quantum states in driven semiconductors. Eur. Phys. J. B 2019, 92, 215. [Google Scholar] [CrossRef] [Green Version]
- Frank, R. Quantum criticality and population trapping of fermions by non-equilibrium lattice modulations. New J. Phys. 2013, 15, 123030. [Google Scholar] [CrossRef] [Green Version]
- Frank, R. Coherent control of Floquet-mode dressed plasmon polaritons. Phys. Rev. B 2012, 85, 195463. [Google Scholar] [CrossRef]
- Frank, R. Non-equilibrium polaritonics - Nonlinear effects and optical switching. Ann. Phys. 2013, 525, 66–73. [Google Scholar] [CrossRef]
- Grifoni, M.; Hänggi, P. Driven quantum tunneling. Phys. Rep. 1998, 304, 229–354. [Google Scholar] [CrossRef]
- Restrepo, S.; Cerrillo, J.; Bastidas, V.M.; Angelakis, D.G.; Brandes, T. Driven Open Quantum Systems and Floquet Stroboscopic Dynamics. Phys. Rev. Lett. 2016, 117, 250401. [Google Scholar] [CrossRef] [Green Version]
- Eckardt, A. Colloquium: Atomic quantum gases in periodically driven optical lattices. Rev. Mod. Phys. 2017, 89, 011004-1. [Google Scholar] [CrossRef]
- Kalthoff, M.H.; Uhrig, G.S.; Freericks, J.K. Emergence of Floquet behavior for lattice fermions driven by light pulses. Phys. Rev. B 2018, 98, 035138. [Google Scholar] [CrossRef] [Green Version]
- Sentef, M.A.; Claassen, M.; Kemper, A.F.; Moritz, B.; Oka, T.; Freericks, J.K.; Devereaux, T.P. Theory of Floquet band formation and local pseudospin textures in pump-probe photoemission of graphene. Nat. Commun. 2015, 6, 7047. [Google Scholar] [CrossRef] [PubMed]
- Yuan, L.; Fan, S. Topologically non-trivial Floquet band structure in a system undergoing photonic transitions in the ultra-strong coupling regime. Phys. Rev. A 2015, 92, 053822. [Google Scholar] [CrossRef]
- Lubatsch, A.; Kroha, J. Optically driven Mott-Hubbard systems out of thermodynamical equilibrium. Ann. Phys. 2009, 18, 863–867. [Google Scholar] [CrossRef]
- Georges, A.; Kotliar, G.; Krauth, W.; Rozenberg, M.J. Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions. Rev. Mod. Phys. 1996, 68, 13. [Google Scholar] [CrossRef]
- Metzner, W.; Vollhardt, D. Correlated Lattice Fermions in d = ∞ Dimensions. Phys. Rev. Lett. 1989, 62, 324. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, P.; Monien, H. Nonequilibrium dynamical mean-field theory of a strongly correlated system. arXiv, 2002; arXiv:0202046. [Google Scholar]
- Maier, T.; Jarrell, M.; Pruschke, T.; Hettler, M.H. Quantum cluster theories. Rev. Mod. Phys. 2005, 77, 1027. [Google Scholar] [CrossRef]
- Freericks, J.K.; Turkowski, V.M.; Zlatic, V. Nonequilibrium Dynamical Mean-Field Theory. Phys. Rev. Lett. 2006, 97, 266408. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tsuji, N.; Oka, T.; Aoki, H. Nonequilibrium Steady State of Photoexcited Correlated Electrons in the Presence of Dissipation. Phys. Rev. Lett. 2009, 103, 047403. [Google Scholar] [CrossRef] [PubMed]
- Lin, N.; Marianetti, C.A.; Millis, A.J.; Reichman, D.R. Dynamical Mean-Field Theory for Quantum Chemistry. Phys. Rev. Lett. 2011, 106, 096402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zgid, D.; Chan, G.K.-L. Dynamical mean-field theory from a quantum chemical perspective. J. Chem. Phys. 2011, 134, 094115. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aoki, H.; Tsuji, N.; Eckstein, M.; Kollar, M.; Oka, T.; Werner, P. Nonequilibrium dynamical mean-field theory and its applications. Rev. Mod. Phys. 2014, 86, 779. [Google Scholar] [CrossRef]
- Frank, R. Population trapping and inversion in ultracold Fermi gases by excitation of the optical lattice-Non-equilibrium Floquet-Keldysh description. Appl. Phys. B 2013, 113, 41–47. [Google Scholar] [CrossRef]
- Sorantin, M.E.; Dorda, A.; Held, K.; Arrigoni, E. Impact ionization processes in the steady state of a driven Mott-insulating layer coupled to metallic leads. Phys. Rev. B 2018, 97, 115113. [Google Scholar] [CrossRef] [Green Version]
- Hofstetter, W.; Qin, T. Topological singularities and the general classification of Floquet-Bloch systems. J. Phys. B At. Mol. Opt. Phys. 2018, 51, 082001. [Google Scholar] [CrossRef]
- Qin, T.; Hofstetter, W. Nonequilibrium steady states and resonant tunneling in time-periodically driven systems with interactions. Phys. Rev. B 2018, 97, 125115. [Google Scholar] [CrossRef] [Green Version]
- Bukov, M.; D’Alessio, L.; Polkovnikov, A. Universal High-Frequency Behavior of Periodically Driven Systems: From Dynamical Stabilization to Floquet Engineering. Adv. Phys. 2015, 64, 139–226. [Google Scholar] [CrossRef]
- Zak, J. Berry’s phase for energy bands in solids. Phys. Rev. Lett. 1989, 62, 2747–2750. [Google Scholar] [CrossRef]
- Xiao, D.; Chang, M.-C.; Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 2009, 82, 1959–2007. [Google Scholar] [CrossRef]
- Gresch, D.; Autes, G.; Yazyev, O.V.; Troyer, M.; Vanderbilt, D.; Bernevig, B.A.; Soluyanov, A.A. Z2Pack: Numerical implementation of hybrid Wannier centers for identifying topological materials. Phys. Rev. B 2017, 95, 075146. [Google Scholar] [CrossRef] [Green Version]
- Chang, P.-C.; Lu, J.G. Temperature dependent conduction and UV induced metal-to-insulator transition in ZnO nanowires. Appl. Phys. Lett. 2008, 92, 212113. [Google Scholar] [CrossRef]
- Chang, P.-C.; Chien, C.-J.; Stichtenoth, D.; Ronning, C.; Lu, J.G. Finite size effect in ZnO nanowires. Appl. Phys. Lett. 2007, 90, 113101. [Google Scholar] [CrossRef] [Green Version]
- Koster, R.S.; Changming, M.F.; Dijkstra, M.; van Blaaderen, A.; van Huis, M.A. Stabilization of Rock Salt ZnO Nanocrystals by Low-Energy Surfaces and Mg Additions: A First-Principles Study. J. Phys. Chem. C 2015, 119, 5648–5656. [Google Scholar] [CrossRef]
- Wegener, M. Extreme Nonliner Optics; Springer: Berlin/Heidelberg, Germany, 2004; ISBN 3-540-22291-X. [Google Scholar]
- King-Smith, R.D.; Vanderbilt, D. Theory of polarization of crystalline solids. Phys. Rev. B 1993, 47, 1651–1654. [Google Scholar] [CrossRef]
- Vanderbilt, D.; King-Smith, R.D. Electric polarization as a bulk quantity and its relation to surface charge. Phys. Rev. B 1993, 48, 4442. [Google Scholar] [CrossRef]
- Resta, R. Macroscopic polarization in crystalline dielectrics: The geometric phase approach. Rev. Mod. Phys. 1994, 66, 899–915. [Google Scholar] [CrossRef]
- Dal Lago, V.; Atala, M.; Foa Torres, L.E.F. Floquet topological transitions in a driven one-dimensional topological insulator. Phys. Rev. A 2015, 92, 023624. [Google Scholar] [CrossRef]
- Gull, E.; Millis, A.; Lichtenstein, A.I.; Rubtsov, A.N.; Troyer, M.; Werner, P. Continuous-time Monte Carlo methods for quantum impurity models. Rev. Mod. Phys. 2011, 83, 349. [Google Scholar] [CrossRef]
- Snoek, M.; Titvinidze, I.; Toke, C.; Byczuk, K.; Hofstetter, W. Antiferromagnetic order of strongly interacting fermions in a trap: Real-space dynamical mean-field analysis. New J. Phys. 2008, 10, 093008. [Google Scholar] [CrossRef]
- Peters, R.; Yoshida, T.; Sakakibara, H.; Kawakami, N. Coexistence of light and heavy surface states in a topological multiband Kondo insulator. Phys. Rev. B 2016, 93, 235159. [Google Scholar] [CrossRef] [Green Version]
- Peters, R.; Yoshida, T.; Kawakami, N. Magnetic states in a three-dimensional topological Kondo insulator. Phys. Rev. B 2018, 98, 075104. [Google Scholar] [CrossRef] [Green Version]
- Franz, W. Einfluß eines elektrischen Feldes auf eine optische Absorptionskante. Z. Naturforschung A 1958, 13, 484–489. [Google Scholar] [CrossRef]
- Keldysh, L.V. The Effect of a Strong Electric Field on the Optical Properties of Insulating Crystals. J. Exptl. Theoret. Phys. 1957, 33, 994–1003, reprinted in Soviet Phys. JETP 1958, 6, 763–770. Available online: jetp.ac.ru/cgi-bin/dn/e_007_05_0788.pdf (accessed on 4 October 2019).
- Keldysh, L.V. Ionization in the Field of a Strong Electromagnetic Wave. J. Exptl. Theoret. Phys. 1964, 47, 1945–1957, reprinted in Soviet Phys. JETP 1964, 20, 1307–1314. Available online: jetp.ac.ru/cgi-bin/dn/e_020_05_1307.pdf (accessed on 4 October 2019).
- Ivanov, A.L.; Keldysh, L.V.; Panashchenko, V.V. Low-threshold exciton-biexciton optical Stark effect in direct-gap semiconductors. Zh. Eksp. Teor. Fiz. 1991, 99, 641–658. [Google Scholar]
- Manmana, S.; Essin, A.M.; Noack, R.M.; Gurarie, V. Topological invariants and interacting one-dimensional fermionic systems. Phys. Rev. B 2012, 86, 205119. [Google Scholar] [CrossRef]
- Rachel, S. Interacting topological insulators: A review. Rep. Prog. Phys. 2018, 81, 116501. [Google Scholar] [CrossRef]
- Miller, D.A.B.; Chemla, D.S.; Damen, T.C.; Gossard, A.C.; Wiegmann, W.; Wood, T.H.; Burrus, C.A. Band-Edge Electroabsorption in Quantum Well Structures: The Quantum-Confined Stark Effect. Phys. Rev. Lett. 1984, 53, 2173–2176. [Google Scholar] [CrossRef]
- Chemla, D.S.; Knox, W.H.; Miller, D.A.B.; Schmitt-Rink, S.; Stark, J.B.; Zimmermann, R. The excitonic optical stark effect in semiconductor quantum wells probed with femtosecond optical pulses. J. Lumin. 1989, 44, 233–246. [Google Scholar] [CrossRef]
- Forn-Diaz, P.; Lamata, L.; Rico, E.; Kono, J.; Solano, E. Ultrastrong coupling regimes of light-matter interaction. Rev. Mod. Phys. 2019, 91, 025005-1. [Google Scholar] [CrossRef]








© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lubatsch, A.; Frank, R. Behavior of Floquet Topological Quantum States in Optically Driven Semiconductors. Symmetry 2019, 11, 1246. https://doi.org/10.3390/sym11101246
Lubatsch A, Frank R. Behavior of Floquet Topological Quantum States in Optically Driven Semiconductors. Symmetry. 2019; 11(10):1246. https://doi.org/10.3390/sym11101246
Chicago/Turabian StyleLubatsch, Andreas, and Regine Frank. 2019. "Behavior of Floquet Topological Quantum States in Optically Driven Semiconductors" Symmetry 11, no. 10: 1246. https://doi.org/10.3390/sym11101246
APA StyleLubatsch, A., & Frank, R. (2019). Behavior of Floquet Topological Quantum States in Optically Driven Semiconductors. Symmetry, 11(10), 1246. https://doi.org/10.3390/sym11101246