1. Introduction
Although train derailment incident is rare, it has attracted a lot of attention for its severe consequences and complex relationship between influencing factors [
1]. When the vehicle departs from the track, accompanied by a huge symmetrical force between wheels and rails, the equipment such as locomotive and vehicle is bound to be damaged, causing a large amount of direct financial loss. Moreover, vehicle derailment can also result in the interruption of train operations and related delays, seriously affecting the quality and efficiency of transport production [
2]. Therefore, much more attention should be paid to derailment risk management, such as human factors, rail parts failure, semaphore and control systems, vehicle-track interaction, and so on [
1,
3]. Risk response is the process to modify risk, and it is not only a crucial sub-process of risk management, but also one of the purposes of risk assessment [
4,
5]. If risk response cannot be implemented effectively, the effect of risk assessment will be affected, causing a negative impact on risk management. However, in risk practice, due to the lack of mature models and tools to choose appropriate response strategies, risk response does not receive enough attention in comparison with risk assessment [
6,
7], and this phenomenon is especially common in the railway industry.
Heinrich’s pyramid [
8] reveals that shunting derailment accidents are usually caused by the interaction of a series of small errors and defects, which involve all aspects of the railway system, such as train operation organization, equipment quality, environmental impact, personnel quality, and fund investment. Therefore, we should find a method that fully considers and weighs the above factors to balance the relationship among benefits, costs, and risks when choosing risk coping strategies, and MCDM can solve the above problems. MCDM is known as a tool for supporting managers in utilizing available information, rethinking the connection, multiple dimensions, and complexity of various factors in the real world, and making it possible to make decisions in the context of different plans [
9,
10,
11]. Currently, the commonly used MCDM technologies are DEMATEL, analytic hierarchy process (AHP), ANP, TOPSIS, simple multi-attribute rating technique etc. However, in many practical problems, it is usually necessary to combine or improve various methods to adapt to practical multi-criteria decision problems [
12,
13,
14,
15]. Nassereddine and Eskandari [
16] set up a hybrid MCDM method to evaluate public transit systems, and the model used the Delphi approach, group AHP and preference ranking organization methodology to enhance the evaluation effect and provide a direction for the improvement of public transit service in the future. Celik et al. [
17] put forward an integrated interval pype-2 fuzzy MCDM model based on TOPSIS and grey relational analysis to promote customer satisfaction in the Istanbul public transit system. Yucel et al. [
18] used a MCDM model based on AHP and the best-worst method for the selection of railway system projects. Lin et al. [
19] used a new fuzzy MCDM technology to select suitable site for car rental outlets. Kabak et al. [
20] used a MCDM model based on GIS to evaluate the shared bike sites.
In the above literature review, we could find that the MCDM model was an efficient tool to settle the multi-criteria problems arising in engineering projects, military science, economic development, humanities, and social sciences. Nevertheless, traditional MCDM methodologies were based on the hypothesis of independence in the evaluation process and did not truly reflect the dependence and interaction relationships among evaluation elements. DEMATEL [
21] was usually used to draw the intricate relationships of interplay in an evaluation index system to screen evaluation indicators, but it could not get the criteria weights, whereas ANP could. ANP was a MCDM method first proven by Saaty in 1996 and was applicable to non-independent hierarchies. Further, the ANP approach had two obvious merits. On the one hand, it reflected the complex dependency among various attributes of the system, rather than a simple hierarchy, on the other hand, it considered the relationship of mutual restriction and interaction among different levels and forms a more comprehensive analysis [
22]. Many scholars have combined the two methods together to construct the multi-criteria decision model. Tadic et al. [
23] built a MCDM model based on fuzzy DEMATEL, fuzzy ANP, and fuzzy VIKOR to solve the problem of urban physical distribution concept options, and the fuzzy ANP was put forward to analyze the criteria weights, while fuzzy DEMATEL was used to determine the strengths of the inner dependencies between the factors, and fuzzy VIKOR method was used to sort the options. Bongo et al. [
24] established a fuzzy MCDM model based on fuzzy set, DEMATEL and ANP methods, and the model was used to reduce congestion at airports which gave negative impact on the punctuality of airlines, the reputation of airports and the travel experience of passengers. Pineda et al. [
25] set up an integrated MCDM technology based on DANP, DEMATEL and VIKOR approach to improve airline operational and financial performance. Lu et al. [
26] built a competitive large-scale airport performance analysis model, and DEMATEL was used to build an intricate lineage illustrated as a network impact diagram. In this approach, DANP was used to confirm the influential weights, and modified VIKOR was used to improve the operating efficiency of international airports. Chen [
27] used a DEMATEL-ANP model to choose a quality improvement standard for airlines in Taiwan, and the study provided many suggestions for airlines to improve the service quality. The TOPSIS method, as a classical method for solving MCDM issues, with the characteristics of a clear concept in addition to simple and small computation, could rank the plans in the solution sets by virtue of virtual ideal solutions and negative ideal solutions [
28]. Currently, the TOPSIS technology, combined with DEMATEL and ANP methods, has been applied to many domains. Buyukozkan and Çifci [
29] put forward a new MCDM model using the fuzzy decision-making trial and evaluation laboratory, fuzzy ANP, and fuzzy TOPSIS to select green suppliers. Liu and Yin [
30] used an integrated approach to select the optimal sustainable energy storing node from the perspective of benefits, opportunities, costs, and risks. Morteza et al. [
31] developed an evaluation model by integrating ANP with fuzzy TOPSIS to get the optimal tourism site. Chen and Chen [
32] used an integrated DEMATEL-Fuzzy ANP-TOPSIS model to evaluate higher education in Taiwan. Nilashi et al. [
33] used a DEMATEL-Fuzzy TOPSIS approach to evaluate factors influencing medical tourism adoption in Malaysia. Hu et al. [
34] developed a DEMATEL-ANP framework to improve air cargo terminal service quality.
Moreover, due to the complexity operating environment and lack of safety information in the railway industry, some difficulties are usually present for managers to analyze the security situation quantitatively, and sometimes it needs expert experience and engineering knowledge to make decisions. Delphi technology, as a prediction method proposed by the Rand Corporation, combines the experience of multiple experts and subjective judgment [
35]. Its core is to conduct several rounds of anonymous consultation to solicit the ideas of experts [
36]. After summarizing and sorting out the opinions of each round, the aggregated information is sent to each expert as reference materials for the experts to analyze, judge and propose new ideas, repeating this for a few times, the experts’ common ground gradually increase, and eventually can obtain a consensus [
37,
38]. Because of its simplicity and practicality, it is often used to solicit expert advice in the MCDM process.
Based on the above analysis, this paper set up a hybrid Delphi-DEMATEL-ANP-TOPSIS model for the selection of derailment risk response strategies. The main contributions of this paper were as follows:
First of all, from the point of literature review, a hybrid MCDM evaluation method was seldom used in train derailment risk response strategies selection, and this study filled the gap. In railway risk response practice, due to the limited resources and technical conditions, experts and scholars usually proposed specific countermeasures through qualitative analysis, but rarely developed specific evaluation models from the perspective of quantitative analysis. The model put forward in this paper could choose the optimal risk response strategy efficiently and quantitatively, providing an effective risk decision-making tool for railway managers.
Secondly, traditional MCDM method was based on the hypothesis of independence in evaluation process and did not truly reflect the dependence and interaction relationships among evaluation elements. The model combined DEMATEL with ANP could not only effectively construct interdependent connections among the risk response criteria, but also overcomed each other’s weaknesses to establish an efficient model. DEMATEL methodology was used to draw the complex “causal coupling” relationships in an evaluation index system to screen evaluation indicators, but it was not suitable for acquiring the criteria weights, whereas ANP could. The ANP approach obtained the weights by analyzing a lot of pair-wise comparison matrices to get the “influence of importance” among the criteria using the Super Decision software, and the calculation results could be used in the TOPSIS method to rank the response strategies.
Thirdly, this model deeply considered the role of secondary risk and residual risk in the process of evaluation criteria selection. In the railway risk practice, because of the cognitive bias on the train derailments, or the inherent mode of thinking, secondary or residual risks (including those not identified by the risk assessment) that might arise during the implementation of the response measures might be ignored, such as the damage of track bed and ecological environment, exposing the existing risk response strategies only considered the primary risks, and the secondary and residual risks might be caused by policy measures were not considered enough, which was easy to affect the achievement of risk response objectives. Risk tradeoff analysis could help us to find out the best strategy to solve problems under the constraints of resources and technology, so as to avoid the phenomenon of “solve one problem only to find another cropping up” [
39]. This study applied tradeoff theory to balance the relationship among benefits, costs, and risks, and took secondary risk and residual risk as the risk response indicators to develop more comprehensive train derailment risk response strategies.
The remaining structure of this paper is as follows:
Section 2 introduces the hybrid MCDM model of this study, including the introduction of Delphi, the process of DEMATEL method, the calculation process of ANP and TOPSIS methods. In
Section 3, the model is applied to select the shunting derailment risk countermeasures in Huangyangcheng station.
Section 4 presents a discussion about the selection of risk response strategies.
Section 5 summarizes the contributions of this research and analyzes the future research directions.
2. The Proposed MCDM Model
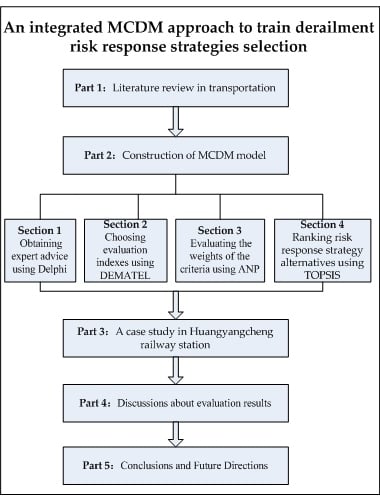
This paper proposed an integrated MCDM model based on Delphi, DEMATEL, ANP and TOPSIS to select sustainable derailment risk response strategy. In this model, the Delphi method was used to acquire expert advice to provide relevant suggestions throughout the whole process. DEMATEL was applied to identify the interdependency and feedback between criteria and finally confirm the key risk response strategy criteria. ANP was applied to acquire the influence of importance between the criteria in addition to deciding the criteria weights. Meanwhile, the TOPSIS approach was used to obtain the ranking of alternative solutions. The model was divided into four sections, and the specific framework was shown in
Figure 1.
2.1. Obtaining Expert Advice Using Delphi
Due to the strong complexity and variability of railway safety, the frequency of some risk events in history was very low, certain railway accidents never happened or rarely happened, or due to the lack of data statistics, relevant information was not comprehensive enough to carry out for quantitative analysis. In such cases, semi-quantitative or qualitative analysis of the system security situation by experienced experts might be sufficient. Based on this, the Delphi method was used to provide expert advice during the process of DEMATEL, ANP, and TOPSIS. The specific process was as follows:
Step 1: Forming a group of experts to define the objectives. In this section, people’s cognitive characteristics were fully considered in the process of expert selection. The inherent decision-making mode of human brain would lead to systematic deviation in people’s judgment of problems, causing them to overestimate some attributes and underestimate others. We corrected this bias by selecting professionals at different levels of experience and theoretical knowledge in the industry to ensure correct advice and valuable judgments.
Step 2: Inviting experts to evaluate the problem. The experts conducted the evaluation anonymously or “back to back” to answer the questions according to the evaluation rules and explain the basis for answering the questions. Multiple rounds of questioning could be conducted on the same issue until a consensus was acquired.
Step 3: Processing of gathering experts’ knowledge. Based on the original opinions of experts, the authors comprehensively considered the factors of consistency and coordination and met the requirements of the convergence of the whole opinions to find the best advice for group decision-making and obtain the conclusion with a credibility index, achieving the purpose of experts’opinions integration.
2.2. Choosing Evaluation Indexes Using DEMATEL
In this stage, the collected risk information was analyzed by experts to preliminarily form a list of criteria, and then DEMATEL method was used to further analyze the coupling relationship and identify the key criteria in terms of their interaction intensity sequence of criteria. The specific steps were as follows:
Step 1: Developing a list of evaluation indicators. The collected train derailment risk data was used to analyze the indicators that affect the selection of derailment strategy by Delphi.
Step 2: Building the direct influence matrix. Assuming there existed the following express instructions: 0 = no influence, 1 = small influence, 2 = moderate influence, 3 = high influence, 4 = great influence. The selected experts were requested to give the degree of direct influence that factor
exerted on factor
, which was denoted by
, and the direct influence matrix
could be expressed by Equation (1):
Step 3: Normalizing the direct influence matrix. Equations (2) and (3) were used for getting the normalized direct relation matrix
:
Step 4: Computation of the total relation matrix. Equation (4) was used to get the total relation matrix, where
was the identity matrix. The row sum and column sum from matrix
were shown in Equations (5) and (6).
where
represented the row sum of the
th row in matrix
, and
represented the column sum of the
th column in matrix
.
denoted the degree of the central role, representing the strength of influence that element
gave and received. If
was positive, then element
was an affecting element, and if
was negative, then element
was an affected element.
Step 5: Drawing a cause and effect diagraph. The graph was drawn using as the horizontal axis and as the vertical axis, and the less influential factors were eliminated.
2.3. Evaluating the Weights of the Criteria Using ANP
The ANP method was a comprehensive decision-making technology, which analyzes the interdependence and feedback relationship among factors in the system with the help of network structure. Therefore, it was considered as a more applicable evaluation and decision-making tool that could more effectively solve complex system problems than AHP. The basic process was as follows:
Step 1: Determination of risk response criteria. Risk criteria were the terms of reference against which the significance of a risk was evaluated. Therefore, risk criteria should reflect the risk tolerance of the organization and reflect the values, goals and resources of the organization [
40].
Step 2: Construction of the ANP network. The experts were required to give advice to determine the influence of sub-criteria on other criteria elements, or the relationship affected by other criteria elements.
Step 3: Calculation of the unweighted super-matrix. Supposing the network had factor sets
,
,
, and
,
,
,
were the elements of set
,
. The factors in criterion set
were compared according to their influence on sub-criterion
, which belonged to set
, so we could get the matrix
, as represented by Equation (7):
if factors in set
were not influenced by factors in set
, then
. For
, repeating the above steps to obtain the super-matrix under a single criterion, as shown in Formula (8):
Step 4: Establishment of the weighted super-matrix. Taking a criterion set as a whole element, the pair-wise comparison was made on the relative importance of a criterion set, and the criterion set was obtained as a normalized weight vector of other criterion sets under a sub-criterion
. Where,
represented the influence weight of the
th subset on the
th subset, and “0” meant no effect,
, the weighted super-matrix is shown by Formula (9):
Step 5: Computation of the limiting super-matrix. We could acquire the limit of each super-matrix relative sorting vector by Equation (10). If the limit was convergent and unique, the value of the corresponding row of the original matrix was the weight of each index.
2.4. Ranking Risk Response Strategy Alternatives Using TOPSIS
TOPSIS was proposed by Hwang and Yoon to help experts calculating positive and negative ideal solutions. The optimal alternative was the one with the least distance from the positive ideal solution and the greatest distance from the negative ideal solution. The steps were summarized as follows:
Step 1: Establishing the initial decision matrix. The initial decision matrix
was constructed according to the original data in the solution set. Where
represented the value of the plan
under the criterion
, the matrix was shown in Equation (11):
Step 2: Normalization of the evaluation matrix. Since there were different dimensions of data in the decision matrix, in order to eliminate the influence of dimensions, it was necessary to normalize the matrix data and obtain the normalized matrix
in Equation (12):
Step 3: Construction of the weighted normalized decision matrix
in Equation (13). Where
was given by
.
Step 4: Determination of the positive and negative ideal solutions. Since attribute indicators could be divided into benefit type and cost type, the solution method for these two types of attribute indicators was shown in Equations (14) and (15).
When
was a benefit indicator,
When
was a cost indicator,
Step 5: Calculation of the separation measure. The separation from the positive and negative ideal for each alternative could be obtained using the n-criteria Euclidean distance, expressed by Equations (16) and (17).
Step 6: Calculation of the relative closeness to the ideal solution
and sorting by priority. Obviously,
lied between 0 and 1, and the larger
was, the more appropriate the plan was, as shown in Equation (18).
5. Conclusions and Future Directions
Train derailment risk response was very important for the safe operation of railways. This paper applied a hybrid MCDM model to select the best derailment risk response strategy. First, the DEMATEL was used to acquire the complex coupling relationship among criteria, and the indicators with a relatively small influence were excluded. Then, ANP and TOPSIS methods were used in the decision-making process, and the weights obtained by the ANP approach were used as the input of the TOPSIS calculation and alternative priorities, thus determining the priority of criteria.
The following contributions were made in this study. Firstly, the technology presented in this paper provided a reliable and simple method for the selection of shunting derailment risk response plans, and realized the change of risk response strategy selection from qualitative to quantitative. Further, a useful tool for railway safety managers to choose the optimal risk response plan was presented. Secondly, many studies had neglected the complex causal relationships among criteria. In this study, the combination of DEMATEL and ANP was used to acquire the criteria and their weights, and a clear map was obtained showing the causal relationships among criteria. Thirdly, the model deeply considered the role of secondary risk and residual risk in the process of evaluation criteria selection. This study applied tradeoff theory to balance the relationship between benefits, costs, and risks, and took secondary risk and residual risk as the risk response indicators to develop more comprehensive train derailment risk response strategies.
Although this model optimized the selection of derailment risk response plans, there were some limitations that could be improved. First of all, the advice came from just eight experts and the experts’ opinions were different because of different knowledge backgrounds. In future work, we could use the fuzzy logic theory to further improve the accuracy of expert evaluation. Secondly, sensitivity analysis should be used to find out the key factors affecting the decision, so as to adopt more effective response strategies. Thirdly, through a comparison with various MCDM methods, we could get the most suitable methods for the selection of risk response strategies.