Frequency Response Evaluation of Guitar Bodies with Different Bracing Systems
Abstract
:1. Introduction
2. The Mathematical Model of the Guitar as a Symmetrical System
Forced Vibrations in Systems with Symmetries
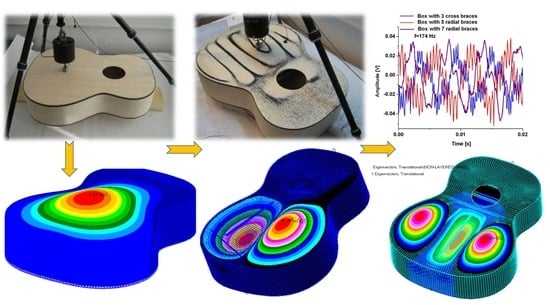
3. Finite Element Analysis (FEA) of the Resonance Body of the Guitar
3.1. Geometrical and Structural Models
3.2. Discretization of Models and Loading
3.3. FEA Results and Discussion
4. The Experimental Analysis to Forced Vibrations
Experimental Set-Up
5. Discussion
6. Conclusions
- Each type of bracing system from guitar body generates the nodal patterns, which overlap with the patterns found from modal analysis (Table 4);
- The first resonance is noticed first, with higher amplitude, then the second, third, etc. All appear at a specific frequency, their resonant frequency and all have different patterns in accordance with bracing systems applied on soundboards;
- In case of forced vibration of 110 Hz, all analyzed structures has one vibration antinode, in a symmetric mode. For 146 Hz, the quasi skew symmetric vibration modes are recorded, has three vibration antinodes with two vertical nodal lines, with vibrating surfaces more or less extended according to bracing patterns;
- The amplitude spectra becomes more complex with increasing the frequency. With increasing the number of bars from bracing systems, the overtones increases too.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dumond, P.; Baddour, N. Effects ofa Scalloped and RectangularBrace on the Modeshapes of a Brace-Plate System. Int. J. Mech. Eng. Mechat. 2012, 1. [Google Scholar] [CrossRef] [Green Version]
- Dumond, P.; Baddour, N. Effects of using scalloped shape braces on the natural frequencies of a brace-soundboard system. App. Acoust. 2012, 73, 1168–1173. [Google Scholar] [CrossRef]
- Okuda, A.; Ono, T. Bracing effect in a guitar top board by vibration experiment and modal analysis. Acoust. Sci. Technol. 2008, 29, 103–105. [Google Scholar] [CrossRef] [Green Version]
- Bader, R. Computational Mechanics of the Classical Guitar; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Hurtado, E.G.; Pedraza-Ortega, J.C.; Ramos-Arreguin, J.-M.; Sotomayor-Olmedo, A.; Perez-Meneses, J. Vibration analysis in the design and construction of an acoustic guitar. Int.J. Phys. Sci. 2012, 7, 1986–1997. [Google Scholar]
- Jansson, E. Acoustics for violin and guitar makers. The Function, Tone, and Tonal Quality of Guitar—Chapter VI, 4th ed. 2002. Available online: http://www.speech.kth.se/music/acviguit4/index.html (accessed on 20 September 2019).
- Christensen, O.; Vistisen, B.B. Simple model for low-frequency guitar function. Catgut Acoust. Soc. Newslett. 1981, 36, 21–27. [Google Scholar]
- Jansson, E.V. A study of the acoustical and hologram interferometric measurements on the top plate vibrations of a guitar. Acustica 1971, 25, 95–100. [Google Scholar]
- Christensen, O. An oscillator model for analysis of guitar sound pressure response. Acustica 1984, 54, 289–295. [Google Scholar]
- Rodríguez, S.E. Numerical Analysis of the Modal Coupling at low resonances in a Colombian Andean Bandola in C using the Finite Element Method. Ph.D. Thesis, Universidad EAFIT, Antioquia, Colombia, 2012. [Google Scholar]
- Stanciu, M.D.; Curtu, I. Analytical and numerical simulation of structures of classical guitar. In Dinamica Structurii Chitarei Clasice (Ro); Printhouse of Transylvania University of Brașov: Brașov, România, 2012; pp. 51–120. Available online: https://www.researchgate.net/publication/272822983_Carte_Dinamica_structurii_chitarei_clasice (accessed on 27 May 2019).
- Ezcurra, A.; Elejabarrieta, M.; Jesús Santamaría, C. Internal Fluid Influence on the Dynamic Behavior of the Resonance Box of the Guitar. Available online: http://www.sea-acustica.es/fileadmin/publicaciones/Sevilla02_mus06015.pdf (accessed on 14 October 2019).
- Elejabarrieta, M.J.; Ezcurra, A.; Santamaría, C. Resonance Box of the Guitar Structure-Fluid Interactio. In Proceedings of the 19th International Congress on Acoustics, Madrid, Spain, 2–7 September 2007. [Google Scholar]
- Elejabarrieta, M.J.; Ezcurra, A.; Santamaria, C. Coupled modes of the resonance box of the guitar. J. Acoust. Soc. Am. 2002, 111, 2283–2292. [Google Scholar] [CrossRef]
- Vladimirovici, S. Calculation Method for the Component Elements of Guitar. Ph.D. Thesis, Technical State Institute Mari, Yoshkar-Ola, Russia, 2004. [Google Scholar]
- Richardson, B.E.; Walker, G.P.; Brooke, M. Synthesis of guitar tones from fundamental parameters relating to construction. Proc. Inst. Acoust. 1990, 12, 757–764. [Google Scholar]
- Šali, S.; Kopač, J. Measuring the quality of guitar tone. Exp. Mech. 2000, 40, 242–247. [Google Scholar] [CrossRef]
- Russell, D. Modal analysis of an Acoustic Folk Guitar. Ph.D. Thesis, Applied Physics, Kettering University, Flint, MI, USA, 1998. [Google Scholar]
- Russel, D.; Pedersen, P. Modal Analyses of an Electric Guitar; Kettering University: Flint, MI, USA, 1999. [Google Scholar]
- Wright, H. The Acoustics and Psychoacoustics of the Guitar. Ph.D. Thesis, University of Wales, College of Cardiff, Cardiff, UK, 1996. [Google Scholar]
- Bécache, E.; Chaigne, A.; Derveaux, G.; Joly, P. Numerical simulation of a guitar. Comput. Struct. 2005, 83, 107–126. [Google Scholar] [CrossRef] [Green Version]
- Torres, J.A.; Boullosa, R.R. Influence of the bridge on the vibrations of the top plate of a classical guitar. Appl. Acoust. 2009, 70, 1371–1377. [Google Scholar] [CrossRef]
- Skrodzka, E.; Łapa, A.; Linde, B.B.J.; Rosenfeld, E. Modal parameters of two incomplete and complete guitars differing in the bracing pattern of the soundboard. J. Acoust. Soc. Am. 2011, 130, 2186–2194. [Google Scholar] [CrossRef] [PubMed]
- Bielski, P.M.; Kujawa, M.; Lubowiecka, I. Modelling and measurement of folk guitar: Truss rod and strings in numerical analysis of tone. Arch. Acoust. 2019, 44, 35–49. [Google Scholar] [CrossRef]
- French, M. Structural modification of stringed instruments. Mech. Syst. Signal Process. 2007, 21, 98–107. [Google Scholar] [CrossRef]
- Besnainou, C.; Frelat, J.; Buys, K. A new concept for string instrument sound board: The splitting board. In Proceedings of the International Symposium on Music Acoustics, Sydney, Australia, 25–27 August 2010; Available online: http://www.lam.jussieu.fr/Publications/Conferences/ISMA2010_Besnainou.pdf (accessed on 11 February 2020).
- Zingoni, A. Group-theoretic exploitations of symmetry in computational solid and structural mechanics. Int. J. Numer. Meth. Eng. 2009, 79, 253–289. [Google Scholar] [CrossRef]
- Mangeron, D.; Goia, I.; Vlase, S. Symmetrical Branched Systems Vibrations. Sci. Mem. Rom. Acad. Buchar. 1991, 12, 232–236. [Google Scholar]
- Vlase, S.; Năstac, D.C.; Marin, M.; Mihălcică, M. A method for the study of the vibration of mechanical bars systems with symmetries. Acta Tech.l Napoc. Ser. Appl. Math. Mech. Eng. 2017, 60, 539. [Google Scholar]
- Alcayde, A.; Velilla, C.; San-Antonio-Gómez, C.; Peña-Fernández, A.; Pérez-Romero, A.; Manzano-Agugliaro, F. Basket-Handle Arch and Its Optimum Symmetry Generation as a Structural Element and Keeping the Aesthetic Point of View. Symmetry 2019, 11, 1243. [Google Scholar] [CrossRef] [Green Version]
- Vlase, S.; Paun, M. Vibration Analysis of a Mechanical System consisting of Two Identical Parts. Ro. J. Techn. Sci. Appl. Mech. 2015, 60, 216–230. [Google Scholar]
- Chen, Y.; Feng, J. Generalized Eigenvalue Analysis of Symmetric Prestressed Structures using Group Theory. J. Comput. Civil. Eng. 2012, 26, 488–497. [Google Scholar] [CrossRef]
- Vlase, S.; Marin, M.; Scutaru, M.L.; Munteanu, R. Coupled transverse and torsional vibrations in a mechanical system with two identical beams. AIP Adv. 2017, 7, 065301. [Google Scholar] [CrossRef]
- Stanciu, M.D.; Vlase, S.; Marin, M. Vibration Analysis of a Guitar considered as a Symmetrical Mechanical System. Symmetry 2019, 11, 727. [Google Scholar] [CrossRef] [Green Version]
- Holm, D.D.; Stoica, C.; Ellis, D.C.P. Group Actions, Symmetries and reduction. In Geometric Mechanics and Symmetry, 1st ed.; Oxford University Press: Oxford, UK, 2009; pp. 184–211. [Google Scholar]
- Curtu, I.; Stanciu, M.D.; Grimberg, R. Correlations between the Plates’ Vibrations from the Guitar’s Structure and the Physical, Mechanical and Elastically Characteristics of the Composite Materials. In Proceedings of the 9th International Conference on Acoustics & Music: Theory & Applications (Amta ’08), Bucharest, Romania, 24–26 June 2008. [Google Scholar]
- Curtu, I.; Stanciu, M.D.; Itu, C.; Grimberg, R. Numerical Modelling of the Acoustic Plates as Constituents of Stringed Instruments. In Proceedings of the 6th International Conference Baltic Industrial Engineering, Tallinn, Estonia, 24–26 April 2008; pp. 53–58. [Google Scholar]
- Curtu, I.; Stanciu, M.D.; Savin, A. The propagation of forced vibrations in coupled plates of guitars. In Proceedings of the 19th International DAAAM Symposium “Intelligent Manufacturing & Automation: Focus on Next Generation of Intelligent Systems and Solutions”, Trnava, Slovakia, 22–25 October 2008; pp. 345–346. [Google Scholar]
- French, M.R. Engineering of Guitar—Theory and Practice; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Lee, M.K.; Fouladi, M.H.; Namasivayam, S.N. Mathematical modelling and acoustical analysis of classical guitars and their soundboards. Adv. Acoust. Vib. 2016, 6084230. [Google Scholar] [CrossRef] [Green Version]
- Boullosa, R.R. Vibration measurements in the classical guitar. Appl. Acoust. 2002, 63, 311–322. [Google Scholar] [CrossRef]
- Huber, T.M.; Beaver, N.; Helps, J.R. Noncontact modal excitation of a classical guitar using ultrasound radiation force. Exp. Tech. 2013, 37, 38–46. [Google Scholar] [CrossRef]
- Urma, D. Acoustic and Music; (print book); Scientific Printhouse: Bucharest, Romania, 1983. (In Romanian) [Google Scholar]
- Ganghoffer, J.F.; Mladenov, I. Similarity, Symmetry and Group Theoretical Methods in Mechanics; Lectures at the International Centre for Mechanical Sciences; CISM: Udine, Italy, 2015. [Google Scholar]
- Lopatin, A.V.; Morozov, E.V. Symmetrical vibration modes of composite sandwich plates. J. Sandw. Struct. Mater. 2010, 13, 189–211. [Google Scholar] [CrossRef]
- Vlase, S. Elimination of Lagrangean Multipliers. Mech. Res. Commun. 1987, 14, 17–20. [Google Scholar] [CrossRef]
- Negrean, I. New Formulations in Analytical Dynamics of Systems. Acta Tech. Napoc. Ser. Appl. Math. Mech. Eng. 2017, 60, 49–56. [Google Scholar]
- Douglas, T. Eigenvalues and Eigenvectors. In Structural Dynamics and Vibrations in Practice: An Engineering Handbook, 1st ed.; Butterworth-Heinemann: Oxford, UK, 2008; pp. 159–180. [Google Scholar]
- Le, K.C.; Nguyen, L.T.K. Energy Methods in Dynamics, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Le, K.C. Vibrations of Shells and Rods; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Bucur, V. Chapter 7- Wood species for musical instruments. In Acoustics of Wood; Springer: Berlin/Heidelberg, Germany, 2006; pp. 171–214. [Google Scholar]
- Sonderegger, W.; Martienssen, A.; Nitsche, C.; Ozyhar, T.; Kaliske, M.; Niemz, P. Investigations on the physical and mechanical behavior of sycamore maple (Acer pseudoplatanus L.). Eur. J. Wood Prod. 2013, 71, 91–99. [Google Scholar] [CrossRef] [Green Version]
- Stanciu, M.D.; Curtu, I.; Itu, C. Influence of strengthening bars of guitar’s plates on the normal modes of vibrations using. In Proceedings of the 19th International DAAAM Symposium “Intelligent Manufacturing & Automation: Focus on Next Generation of Intelligent Systems and Solutions”, Trnava, Slovakia, 22–25 October 2008; pp. 1295–1296. [Google Scholar]

















| Physical and Mechanical Properties of Wood | Top Plate Spruce | Backplate/Sides Maple | |
|---|---|---|---|
| Density (kg/m3) | 420 | 685 | |
| Length of guitar body (mm) | 480 | 480 | |
| Width of guitar body (mm) | 380 | 380 | |
| Height of guitar body (mm) | 100 | 100 | |
| Thickness of plate (mm) | 2.5 | 2.5 | |
| Young’s moduli (MPa) | EL | 14,128 | 11,000 |
| ER | 8310 | 6471 | |
| ET | 1441 | 1122 | |
| Shear moduli (MPa) | GRT | 5730 | 1200 |
| GLT | 1975 | 414 | |
| GLR | 1273 | 267 | |
| Poisson ratio | νLR | 0.45 | 0.44 |
| νRL | 0.03 | 0.09 | |
| νLT | 0.54 | 0.48 | |
| νTL | 0.019 | 0.036 | |
| νRT | 0.56 | 0.78 | |
| νTR | 0.3 | 0.38 | |
| Type of Guitar Body | Frequency [Hz] at Maximum Amplitudes | ||||
|---|---|---|---|---|---|
| C3BT | 200/220 | 320/340 | 600 | ||
| C3BR2T | 240 | 280 | 400 | ||
| C5BR2T | 200 | 300 | 400 | 620 | 780 |
| Excitation frequency [Hz] | 110 | 146 | 196 | 246 | 329 | 413 | 440 | 588 | 720 | 980 |
| Voltage of signal amplification [V] | 1.8 | 1.8 | 1.2 | 1.2 | 1.2 | 1.5 | 2.1 | 3.5 | 3.1 | 1.5 |
| Amperage [A] | 0.5 | 0.5 | 0.3 | 0.3 | 0.3 | 0.3 | 0.4 | 0.7 | 0.7 | 0.3 |
| Types of Strutting System |  |  |  |  |  |
|---|---|---|---|---|---|
| C3BT | C3BR2T | C5BR2T | C7BR2T | C3BR2V | |
| 110 Hz Symm |  (1,1)1 |  (1,1)1 |  (1,1)1 |  (1,1)1 |  (1,1)1 |
| 146 Hz Quasi Skew Symm |  (1,1) |  (1,3)1 |  (1,3)1 |  (1,3)1 |  (1,3)1 |
| 196 Hz Symm. |  (1,1) |  (1,1)2 |  (1,1)2 |  (1,1)2 |  (1,1)2 |
| 246 Hz Symm. |  (1,1) |  (1,1)3 |  (1,1)3 |  (1,1)3 |  (1,1)3 |
| 329 Hz Skew Symm. |  (0,1) |  (2,3)1 |  (1,3)1 |  (1,2) |  (1,2) |
| 440 Hz Skew Symm. |  (2,1)2 |  (1,4) |  (1,3)2 |  (2,3)1 |  (1,3) |
| 588 Hz Quasi Skew Symm |  (1,3) |  (1,5) |  (1,5) |  (2,3)2 |  (1,4) |
| 720 Hz Quasi Skew Symm. |  (3,3) |  (1,6) |  (1,6) |  (1,5) |  (1,5) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mihălcică, M.; Stanciu, M.D.; Vlase, S. Frequency Response Evaluation of Guitar Bodies with Different Bracing Systems. Symmetry 2020, 12, 795. https://doi.org/10.3390/sym12050795
Mihălcică M, Stanciu MD, Vlase S. Frequency Response Evaluation of Guitar Bodies with Different Bracing Systems. Symmetry. 2020; 12(5):795. https://doi.org/10.3390/sym12050795
Chicago/Turabian StyleMihălcică, Mircea, Mariana D. Stanciu, and Sorin Vlase. 2020. "Frequency Response Evaluation of Guitar Bodies with Different Bracing Systems" Symmetry 12, no. 5: 795. https://doi.org/10.3390/sym12050795
APA StyleMihălcică, M., Stanciu, M. D., & Vlase, S. (2020). Frequency Response Evaluation of Guitar Bodies with Different Bracing Systems. Symmetry, 12(5), 795. https://doi.org/10.3390/sym12050795