Malware Classification Using Simhash Encoding and PCA (MCSP)
Abstract
:1. Introduction
2. Background
2.1. Static, Dynamic and Hybrid Approaches
2.2. Simhash, N-Gram, MCSC Image and N-Gram MCSC
2.3. Principal Component Analysis (PCA)
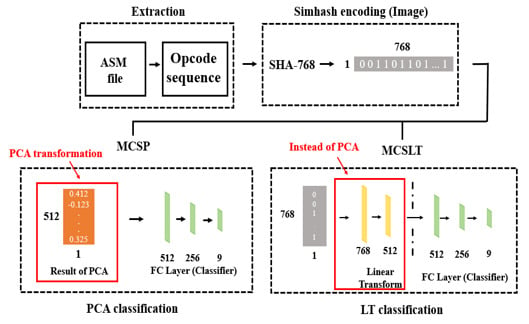
3. Proposed Methods
3.1. Experimental Dataset
3.2. Method 1: Malware Classification Using Simhah Encoding and PCA (MCSP)
3.3. Method 2: Malware Classification Using Simhash Encoding and Linear Transformation Layer (MCSLT)
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gandotra, E.; Bansal, D.; Sofat, S. Malware analysis and classification: A survey. J. Inf. Secur. 2014, 2014, 44440. [Google Scholar] [CrossRef] [Green Version]
- Lu, R. Malware Detection with LSTM using Opcode Language. arXiv 2019, arXiv:1906.04593. [Google Scholar]
- Nataraj, L.; Yegneswaran, V.; Porras, P.; Zhang, J. A comparative assessment of malware classification using binary texture analysis and dynamic analysis. Available online: http://www.csl.sri.com/users/vinod/papers/aisec17-nataraj.pdf (accessed on 2 March 2020).
- Ni, S.; Qian, Q.; Zhang, R. Malware identification using visualization images and deep learning. Comput. Secur. 2018, 77, 871–885. [Google Scholar] [CrossRef]
- Sun, G.; Qian, Q. Deep learning and visualization for identifying malware families. IEEE Trans. Dependable Secure Comput. 2018. [Google Scholar] [CrossRef]
- Damodaran, A.; Di Troia, F.; Visaggio, C.A.; Austin, T.H.; Stamp, M. A comparison of static, dynamic, and hybrid analysis for malware detection. J. Comput. Virol. Hacking Tech. 2017, 13, 1–12. [Google Scholar] [CrossRef]
- Charikar, M.S. Similarity estimation techniques from rounding algorithms. In Proceedings of the thiry-fourth annual ACM symposium on Theory of computing, Montreal, QC, Canada, 19–20 May 2020; pp. 380–388. [Google Scholar]
- Witten, I.H.; Frank, E. Data mining: Practical machine learning tools and techniques with Java implementations. Acm Sigmod Rec. 2002, 31, 76–77. [Google Scholar] [CrossRef]
- Poudyal, S.; Dasgupta, D.; Akhtar, Z.; Gupta, K. A multi-level ransomware detection framework using natural language processing and machine learning. In Proceedings of the 14th International Conference on Malicious and Unwanted Software” MALCON, Nantucket, MA, USA, 2–4 October 2019. [Google Scholar]
- Lim, M.J.; Kwon, Y.M. Efficient algorithm for malware classification: N-gram MCSC. Int. J. Comput. Digit. Syst. 2020, 9, 179–185. [Google Scholar]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Zhang, T.; Yang, B. Big data dimension reduction using PCA. In Proceedings of the IEEE International Conference on Smart Cloud (SmartCloud), New York, NY, USA, 18–20 November 2016; pp. 152–157. [Google Scholar]
- Ronen, R.; Radu, M.; Feuerstein, C.; Yom-Tov, E.; Ahmadi, M. Microsoft malware classification challenge. arXiv 2018, arXiv:1802.10135. [Google Scholar]
- Krawczyk, B. Learning from imbalanced data: Open challenges and future directions. Prog. Artif. Intell. 2016, 5, 221–232. [Google Scholar] [CrossRef] [Green Version]
- Dang, Q.H. Secure hash standard; (No. Federal Inf. Process. Stds.(NIST FIPS)-180-4); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2015.
- Miller, R.G., Jr. Beyond ANOVA: Basics of applied statistics; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Van Asch, V. Macro-and micro-averaged evaluation measures. Available online: https://pdfs.semanticscholar.org/1d10/6a2730801b6210a67f7622e4d192bb309303.pdf (accessed on 2 February 2020).








| Layer (Type) | Output Shape | Param # | Remarks |
|---|---|---|---|
| Conv2d | [−1, 32, 31, 31] | 160 | |
| Tanh | [−1, 32, 31, 31] | 0 | |
| Conv2d | [−1, 32, 30, 30] | 4128 | |
| Tanh | [−1, 32, 30, 30] | 0 | |
| MaxPool2d | [−1, 32, 15, 15] | 0 | |
| Dropout2d | [−1, 32, 15, 15] | 0 | |
| Conv2d | [−1, 32, 14, 14] | 4128 | |
| Tanh | [−1, 32, 14, 14] | 0 | |
| MaxPool2d | [−1, 32, 7, 7] | 0 | |
| Dropout2d | [−1, 32, 7, 7] | 0 | |
| Linear | [−1, 512] | 803,328 | | |
| Tanh | [−1, 512] | 0 | | |
| Linear | [−1, 256] | 131,328 | | FC classifier |
| Tanh | [−1, 256] | 0 | | |
| Linear | [−1, 9] | 2313 | | |
| Virus Name | Number of Files | TYPE |
|---|---|---|
| Ramnit | 1532 | Worm |
| Lollipop | 2470 | Adware |
| Kelihos_ver3 | 2937 | Backdoor |
| Vundo | 447 | Trojan |
| Simda | 39 | Backdoor |
| Tracur | 732 | TrojanDownloader |
| Kelihos_ver1 | 387 | Backdoor |
| Obfuscator.ACY | 1179 | Any kind of obfuscated malware |
| Gatak | 1013 | Backdoor |
| N-Gram | The Size of the Vocabulary Dictionary of N-Gram |
|---|---|
| 1-gram | 231 |
| 2-gram | 24,920 |
| 3-gram | 24,916 |
| 4-gram | 24,910 |
| The Number of PCA Axis\N-Gram | 1-Gram | 2-Gram | 3-Gram | 4-Gram |
|---|---|---|---|---|
| The number of PCA axis for 95% explained variance | 141 | 316 | 441 | 510 |
| The number of PCA axis for 90% explained variance | 53 | 162 | 278 | 358 |
| Methods | FC Classifier | MCSC (tanh, relu) | MCSP | MCSLT |
|---|---|---|---|---|
| Model + Classifier layers | 393,728 + 133,641 | 811,744 + 133,641 | 262,656 + 133,641 | 1246976 + 133,641 |
| The total number of parameters | 527,369 | 945,385 | 396,297 | 1,477,641 |
| N-Gram\Methods | FC Classifier | tanhMCSC | reluMCSC | MCSP | MCSLT | |
|---|---|---|---|---|---|---|
| 1-gram | Mean | 94.73 | 94.40 | 94.48 | 95.13 | 94.95 |
| Max | 95.07 | 94.65 | 94.79 | 95.30 | 95.16 | |
| Std | 0.0020 | 0.0012 | 0.0017 | 0.0007 | 0.0011 | |
| 2-gram | Mean | 97.47 | 97.53 | 97.60 | 98.16 | 97.95 |
| Max | 97.86 | 98.04 | 97.91 | 98.42 | 98.28 | |
| Std | 0.0018 | 0.0018 | 0.0014 | 0.0007 | 0.0017 | |
| 3-gram | Mean | 97.21 | 97.80 | 97.80 | 98.60 | 98.04 |
| Max | 97.22 | 98.09 | 98.00 | 98.74 | 98.46 | |
| Std | 0.0031 | 0.0014 | 0.0016 | 0.0008 | 0.0019 | |
| 4-gram | Mean | 96.71 | 97.46 | 97.60 | 98.47 | 97.85 |
| Max | 97.63 | 97.81 | 97.81 | 98.56 | 98.23 | |
| Std | 0.0033 | 0.0018 | 0.0014 | 0.0005 | 0.0020 | |
| Methods | Ramnit | Lolli pop | Kelihos_ ver3 | Vundo | Simda | Tracur | Kelihos_ ver1 | Obfuscator. ACY | Gatak | Mean Score | Weighted Mean Score | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1-gram | tanhMCSC | 0.8193 | 0.9539 | 0.9999 | 0.9924 | 0.8524 | 0.9005 | 1 | 0.9159 | 0.9868 | 0.9357 | 0.9357 |
| reluMCSC | 0.8417 | 0.9574 | 1 | 0.9924 | 0.8571 | 0.9084 | 1 | 0.9185 | 0.9859 | 0.9372 | 0.9694 | |
| MCSP | 0.8213 | 0.9699 | 1 | 0.9981 | 0.8571 | 0.918 | 1 | 0.9281 | 0.9948 | 0.9431 | 0.9696 | |
| MCSLT | 0.8146 | 0.9676 | 1 | 0.9936 | 0.8571 | 0.9126 | 1 | 0.9328 | 0.9924 | 0.9412 | 0.9685 | |
| 2-gram | tanhMCSC | 0.9556 | 0.9814 | 1 | 0.9962 | 0.8095 | 0.9267 | 1 | 0.9425 | 0.9826 | 0.9549 | 0.9549 |
| reluMCSC | 0.9565 | 0.981 | 1 | 0.9951 | 0.8429 | 0.9336 | 1 | 0.9432 | 0.9832 | 0.9595 | 0.9779 | |
| MCSP | 0.963 | 0.9868 | 1 | 1 | 0.9333 | 0.9397 | 1 | 0.9555 | 0.9948 | 0.9748 | 0.9869 | |
| MCSLT | 0.9611 | 0.9834 | 1 | 0.9951 | 0.9476 | 0.932 | 0.9982 | 0.957 | 0.989 | 0.9737 | 0.9861 | |
| 3-gram | tanhMCSC | 0.9643 | 0.9767 | 0.9984 | 0.9788 | 0.7143 | 0.9724 | 0.9958 | 0.953 | 0.979 | 0.9481 | 0.9481 |
| reluMCSC | 0.9608 | 0.9731 | 0.9988 | 0.9742 | 0.7333 | 0.9756 | 0.9970 | 0.9503 | 0.9782 | 0.9490 | 0.9719 | |
| MCSP | 0.9717 | 0.9897 | 1 | 1 | 0.9857 | 0.9795 | 0.9848 | 0.9592 | 0.9892 | 0.9844 | 0.9920 | |
| MCSLT | 0.9603 | 0.9842 | 0.9997 | 0.9898 | 0.7524 | 0.9749 | 0.9873 | 0.9536 | 0.9844 | 0.9541 | 0.9745 | |
| 4-gram | tanhMCSC | 0.9647 | 0.9782 | 0.9971 | 0.9697 | 0.7762 | 0.9231 | 0.9855 | 0.9583 | 0.9763 | 0.9477 | 0.9477 |
| reluMCSC | 0.9592 | 0.9784 | 0.9988 | 0.9723 | 0.9000 | 0.9260 | 0.9891 | 0.9667 | 0.9763 | 0.963 | 0.9802 | |
| MCSP | 0.9779 | 0.9886 | 1 | 0.9886 | 0.6857 | 0.9797 | 0.9945 | 0.9595 | 0.9796 | 0.9505 | 0.9716 | |
| MCSLT | 0.9658 | 0.9844 | 0.998 | 0.9784 | 0.7429 | 0.9562 | 0.9909 | 0.9525 | 0.978 | 0.9497 | 0.9718 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwon, Y.-M.; An, J.-J.; Lim, M.-J.; Cho, S.; Gal, W.-M. Malware Classification Using Simhash Encoding and PCA (MCSP). Symmetry 2020, 12, 830. https://doi.org/10.3390/sym12050830
Kwon Y-M, An J-J, Lim M-J, Cho S, Gal W-M. Malware Classification Using Simhash Encoding and PCA (MCSP). Symmetry. 2020; 12(5):830. https://doi.org/10.3390/sym12050830
Chicago/Turabian StyleKwon, Young-Man, Jae-Ju An, Myung-Jae Lim, Seongsoo Cho, and Won-Mo Gal. 2020. "Malware Classification Using Simhash Encoding and PCA (MCSP)" Symmetry 12, no. 5: 830. https://doi.org/10.3390/sym12050830
APA StyleKwon, Y. -M., An, J. -J., Lim, M. -J., Cho, S., & Gal, W. -M. (2020). Malware Classification Using Simhash Encoding and PCA (MCSP). Symmetry, 12(5), 830. https://doi.org/10.3390/sym12050830