Method of Third-Order Convergence with Approximation of Inverse Operator for Large Scale Systems
Abstract
:1. Introduction
2. LC study for the Method in Equation (7)
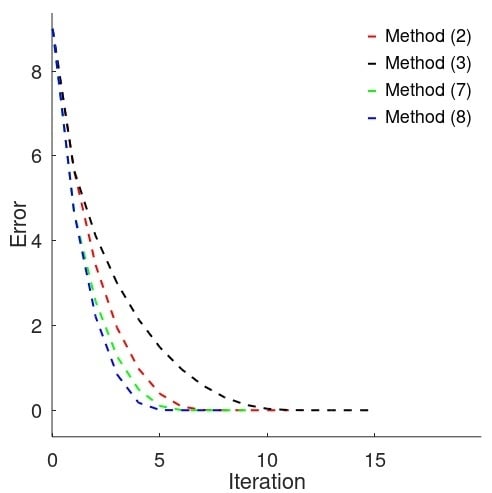
3. Numerical Experiments
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Argyros, I.K. Convergence and Applications of Newton-Type Iterations; Springer: New York, NY, USA, 2008; 506p. [Google Scholar]
- Amat, S.; Busquier, S.; Plaza, S. Review of some iterative root–finding methods from a dynamical point of view. Ser. A Math. Sci. 2004, 10, 3–35. [Google Scholar]
- Amat, S.; Busquier, S.; Plaza, S. Dynamics of King’s and Jarratt iterations. Aequ. Math. 2005, 69, 212–223. [Google Scholar] [CrossRef]
- Kantorovich, L.V.; Akilov, G.P. Functional Analysis; Nauka: Moscow, Russia, 1977; 744p. [Google Scholar]
- Magrenan, A.A. Different anomalies in a Jarratt family of root-finding methods. Appl. Math. Comput. 2014, 233, 29–38. [Google Scholar]
- Rooze, A.F. An iterative method for solving nonlinear equations using parallel inverse operator approximation. Izv. Acad. Nauk Est. SSR Fiz. Mat. 1982, 31, 32–37. (In Russian) [Google Scholar]
- Rooze, A.F. An asynchronous iteration method of solving non-linear equations using parallel approximation of an inverse operator. USSR Comput. Math. Math. Phys. 1986, 26, 188–191. (In Russian) [Google Scholar] [CrossRef]
- Iakymchuk, R.; Shakhno, S. Methods with successive and parallel approximations of inverse operator for the nonlinear least squares problem. Proc. Appl. Math. Mech. 2015, 15, 569–570. [Google Scholar] [CrossRef] [Green Version]
- Ulm, S. On iterative methods with successive approximation of the inverse operator. Izv. Acad. Nauk Est. SSR Fiz. Mat. 1967, 16, 403–411. (In Russian) [Google Scholar]
- Argyros, I.K. On Ulm’s method for Fréchet differentiable operators. J. Appl. Math. Comput. 2005, 31, 97–111. [Google Scholar] [CrossRef]
- Argyros, I.K. On Ulm’s method using divided differences of order one. Numer. Algorithms 2009, 52, 295–320. [Google Scholar] [CrossRef]
- Burmeister, W. Inversionfreie Verfahren zur Lösung nichtlinearer Operatorgleichungen. ZAMM 1972, 52, 101–110. [Google Scholar] [CrossRef]
- Ulm, S. On generalized divided differences. Izv. Acad. Nauk. Est. SSR Fiz. Mat. 1967, 16, 13–26. (In Russian) [Google Scholar]
- Shakhno, S.M. Convergence of one iterative method with successive approximation of inverse operator. Visnyk Lviv. Univ. Ser. Mech. Math. 1989, 31, 62–66. (In Ukrainian) [Google Scholar]
- Shakhno, S.M.; Yarmola, H.P. Two-step secant type method with approximation of the inverse operator. Carpathian Math. Publ. 2013, 5, 150–155. (In Ukrainian) [Google Scholar] [CrossRef] [Green Version]
- Vaarmann, O. On some iterative methods with successive approximation of the inverse operator. I. Izv. Acad. Nauk Est. SSR Fiz. Mat. 1968, 17, 379–387. (In Russian) [Google Scholar]
- Verzhbitskiy, V.M. Iterative methods with successive approximation of inverse operators. Izv. IMI UdGU 2006, 2, 129–138. (In Russian) [Google Scholar]
- Vaarmann, O. On some iterative methods with successive approximation of the inverse operator. II. Izv. Acad. Nauk Est. SSR Fiz. Mat. 1969, 18, 14–21. (In Russian) [Google Scholar]
- Vasilyev, F.P.; Khromova, L.M. On high-order methods for solving operator equations. Dokl. Nauk SSSR 1983, 270, 28–31. (In Russian) [Google Scholar]
- Esquerro, J.A.; Hernández, M.A.; Salanova, M.A. A discretization scheme for some conservative problems. J. Comp. Appl. Math. 2000, 115, 181–192. [Google Scholar] [CrossRef] [Green Version]
- Esquerro, J.A.; Hernández, M.A. An Ulm-type method with R-order of convergence three. Nonlinear Anal. Real World Appl. 2012, 12, 14–26. [Google Scholar] [CrossRef]
- Luksan, L. Inexact trust region method for large sparse systems of nonlinear equations. J. Optim. Theory Appl. 1994, 81, 569–590. [Google Scholar] [CrossRef] [Green Version]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Argyros, I.K.; Shakhno, S.; Yarmola, H. Method of Third-Order Convergence with Approximation of Inverse Operator for Large Scale Systems. Symmetry 2020, 12, 978. https://doi.org/10.3390/sym12060978
Argyros IK, Shakhno S, Yarmola H. Method of Third-Order Convergence with Approximation of Inverse Operator for Large Scale Systems. Symmetry. 2020; 12(6):978. https://doi.org/10.3390/sym12060978
Chicago/Turabian StyleArgyros, Ioannis K., Stepan Shakhno, and Halyna Yarmola. 2020. "Method of Third-Order Convergence with Approximation of Inverse Operator for Large Scale Systems" Symmetry 12, no. 6: 978. https://doi.org/10.3390/sym12060978
APA StyleArgyros, I. K., Shakhno, S., & Yarmola, H. (2020). Method of Third-Order Convergence with Approximation of Inverse Operator for Large Scale Systems. Symmetry, 12(6), 978. https://doi.org/10.3390/sym12060978