Charge Asymmetry in Top Quark Pair Production

Abstract

The top quark is the heaviest elementary particle known. It has been proposed many times that new physics beyond the current theory of elementary particles may reveal itself in top quark interactions. The charge asymmetry in the pair production of a fermion and its antiparticle has been known for many decades. Early measurements of such asymmetry in top quark pair production showed a disagreement with the prediction by more than 3 standard deviations. Many years of an effort on both experimental and theoretical side have allowed to understand the top quark pair charge asymmetry better and to bring back the agreement between the measurements and the theory. In this article, these efforts are reviewed together with the discussion about a potential future of such measurements.

1. Introduction

The Standard Model (SM) of particles is a quantum field theory which describes strong and electroweak interactions [1,2,3]. During the past about 40 years, it has been successfully tested in a large number of experiments which performed numerous measurements. However, the SM has its shortcomings. For example, it has too many free parameters, there is an absence of the explanation for the observed amount of dark matter [4], and the prediction for the matter–antimatter asymmetry is way too low compared to the observation [5]. There have been many theoretical attempts to overcome SM shortcomings. On the other hand, the experimentalists have been trying to find a discrepancy between predictions and measurements. This would serve as a hint for a more complex theory going beyond the Standard Model (BSM) framework.

The top quark is one of the fundamental fermions, spin-half particles, in the SM. It has a large mass ($m_t=173\pm 0.4$ GeV [6]), much larger than a mass of any other quark or lepton (the next heaviest quark, b quark is about 40 times lighter). This means the top quark may play a special role in BSM theories or the BSM physics may reveal first in the interactions involving the top quark [7,8]. Another consequence of its large mass is that it has a very short lifetime so it has no time to hadronize. Top quark properties are thus transferred to its decay products. From an experimental point of view, it is important that top quark properties can be studied without a complication from the hadronization, unlike with any other quark.

The top quark has been observed in the experiments at only two accelerators: in proton–antiproton ($p\overline{p}$) collisions at the Tevatron in Fermilab, USA and in proton–proton ($pp$) collisions at the Large Hadron Collider (LHC) at the European Organization for Nuclear Research (CERN), Switzerland. The top quark was observed for the first time in 1995 at the Tevatron in a data taking period called ‘Run I’ at a center-of-mass energy of interactions of $\sqrt{s}=1.8$ TeV by CDF and D0 experiments [9,10]. The Run I took place during 1992–1996 and the amount of data collected per experiment corresponded to about $100{\mathrm{pb}}^{-1}$ of the integrated luminosity. Only a few tens of top–antitop ($t\overline{t}$) pair candidate events were collected at both experiments. The second data period (Run II) at the Tevatron happened during 2001–2011 at a bit larger energy of $\sqrt{s}=1.96$ TeV. Overall, about a hundred times more data ($10{\mathrm{fb}}^{-1}$) were collected by each experiment. This amount of data allowed detailed measurements of top quark properties although a lot of the measurements have been statistically limited. The LHC started its operation in 2008, but after the incident a few days later, the first collisions at $\sqrt{s}=7$ TeV happened only in 2010. The center-of-mass energy of $pp$ collisions (and the luminosity) has gradually risen from $\sqrt{s}=7$ TeV in 2010 ($5{\mathrm{fb}}^{-1}$) to $\sqrt{s}=8$ TeV in 2011–2012 ($20{\mathrm{fb}}^{-1}$) and $\sqrt{s}=13$ TeV in 2015–2018 ($150{\mathrm{fb}}^{-1}$) with the shutdown happening in 2013–2014. The data taking period from 2010–2012 is called “Run 1” while the second data taking period between 2015–2018 is called “Run 2”. At present, there is another accelerator shutdown which is planned for years 2019–2021. Given the much higher energy of interactions and much larger luminosity at the LHC compared to the Tevatron, many more top quarks have been produced which allowed for much more detailed measurements of top quark properties.

One of the top quark properties which has been studied is a charge asymmetry in the top quark pair production. This means there is a difference in the angular distribution for top and antitop quarks with respect to a given direction. It is a small effect in the SM [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32] which could be greatly enhanced by various BSM models [33,34,35,36,37,38,39]. The initial measurements at the Tevatron observed larger asymmetries than predicted by the SM at that time [40,41,42,43,44]. A few deviations larger than two standard deviations (SD) were observed by both experiments, with the largest deviation of more than 3 SD observed by the CDF experiment at a large invariant mass of the top quark pair [42].

The unexpectedly large measured charge asymmetries started a huge interest in both theoretical and experimental communities in studying this effect in a much more detail. Theoretical physicists calculated the asymmetry more precisely within the SM [17,18,19,20,21,22,24,25,26,28,29,30,31,32] and also tried to explain it with many new BSM models, see Refs. [45,46] and references therein. A few years ago the full next-to-next-leading order (NNLO) prediction in quantum chromodynamics (QCD) for the top quark pair production [47,48] and later for the $t\overline{t}$ charge asymmetry became available [30,31,32]. The experiments studied the underlying effect at both the Tevatron and the LHC, using different channels, studying various observables, and measuring the asymmetry in more detail differentially. The experiments at the Tevatron and the LHC are complementary. They can not measure the exact same asymmetry, rather two different observables based on the same underlying cause. There are advantages and disadvantages to perform the measurements at both colliders. The advantage at the Tevatron is that the predicted asymmetry (≈10%) is about an order of magnitude larger compared to the LHC (≈1%). On the other hand, the disadvantage at the Tevatron compared to the LHC is a limited data statistics. The non-zero forward–backward asymmetry has been already observed (≥5 SD) at the Tevatron a few years ago [49], while one of the LHC experiments, A Toroidal LHC Apparatus (ATLAS), has been able to see the evidence (≥3 SD) for a non-zero charge asymmetry for the first time only the last year [50].

Given that large theoretical and experimental progress in the $t\overline{t}$ charge asymmetry during the past more than 10 years, the review of these studies is in order which this article tries to address. In the next section, the basic description of the top quark charge asymmetry and its various definitions are provided. Section 3 gives a brief overview of theoretical predictions for the charge asymmetry expected in the SM at various orders in the perturbative theory and also for various BSM models. In Section 4, the review of both Tevatron and LHC measurements is presented. In Section 5 follows a discussion of current results and the outlook for next measurements at the LHC and future colliders with the conclusion being in Section 6.

2. Charge Asymmetry in $\mathit{t}\overline{\mathit{t}}$ Production

In this section, the top quark production within the SM is described. Afterwards, the charge asymmetry is discussed within the quantum electrodynamics (QED), the electroweak (EW) theory, the quantum chromodynamics, and specifically in the top quark pair production. Finally, a few different definitions of the asymmetry will be mentioned which have been used in the measurements and theoretical predictions.

2.1. Top Quark Production in the SM at Hadron Colliders

At hadron colliders, the dominant production of the top quark is via the top–antitop ($t\overline{t}$) pair production through strong interactions described by QCD. At the lowest, leading order (LO) of the perturbative QCD, the top-quark pair (when talking about the top quark pair, it is always assumed the top–antitop pair, unless stated otherwise) production is possible through the quark–antiquark annihilation ($q\overline{q}\to t\overline{t}$) or the gluon fusion ($gg\to t\overline{t}$). Feynman diagrams of the LO $t\overline{t}$ production are shown in Figure 1. At higher orders, e.g., next-to-leading (NLO) or next-to-next-to-leading (NNLO), the $t\overline{t}$ production is possible also through the quark–gluon interaction ($gq\to t\overline{t}$ or $g\overline{q}\to t\overline{t}$).

The top (antitop) quark alone can not be produced in QCD due to the flavour conservation. However, the flavour is not conserved in weak interactions. Therefore, a single top quark can be produced, see Figure 2. Since the strong coupling constant ${\alpha }_s$ is the largest of all couplings, the $t\overline{t}$ pair production has a cross-section larger than the single-top production even though there are two top quarks produced.

The $t\overline{t}$ pair production mechanism is quite different at the Tevatron and at the LHC. In $p\overline{p}$ collisions at the Tevatron in Run II at $\sqrt{s}=1.96$ TeV, the dominant $t\overline{t}$ production is through the $q\overline{q}$ annihilation ( 85% $q\overline{q}$ and 15% $gg$ at LO in QCD [6]). At the LHC in $pp$ interactions, it is almost opposite. The gluon fusion production channel is dominant, being about 80–90% at LO when going from $\sqrt{s}=7$ TeV to $\sqrt{s}=14$ TeV [6].

There are a few $t\overline{t}$ inclusive cross-section predictions available at NNLO or higher in QCD. The initial NNLO calculation became available in Ref. [47]. This included later the higher-order soft-gluon corrections through the resummation at the next-to-next-leading-logarithm (NNLL) accuracy, see [48] and references therein. Based on the above NNLO calculation and adding next-to-next-to-next-to-leading-order (${\mathrm{N}}^3$LO) soft-gluon corrections by applying a different method, the approximate ${\mathrm{N}}^3$LO (${\mathrm{aN}}^3$LO) prediction became available [51]. Recently, there was performed another independent calculation of the $t\overline{t}$ production at NNLO QCD using the matrix framework [52,53,54].

The cross-section predictions of the $t\overline{t}$ pair production are shown in

Table 1. The predicted next-to-next-to-leading order (NNLO) $t\overline{t}$ production cross-sections in pb for various energies at the Tevatron and at the Large Hadron Collider (LHC) and for different available calculations. The uncertainties include the factorization and renormalization scale and parton distribution function (PDF)+${\alpha }_s$ uncertainties. The assumed top quark mass is always $m_t=173.3$ GeV except for NNLO + next-to-next-leading-logarithm (NNLL) prediction at the LHC where it is $m_t=173.2$ GeV.

Collider	$\sqrt{\mathit{s}}$ [TeV]	NNLO + NNLL [48]	aN3LO [51]	NNLO [54]
Tevatron	1.96	${7.16}_{-0.23}^{+0.20}$	$7.37\pm 0.39$
LHC	7	${174}_{-11}^{+10}$	${174}_{-12}^{+11}$
LHC	8	${248}_{-14}^{+13}$	${248}_{-15}^{+14}$
LHC	13	${816}_{-45}^{+39}$	${810}_{-36}^{+38}$	${794}_{-45}^{+28}$

for both the Tevatron and the LHC, for different center-of-mass energies, and for different calculations. The values are very similar and consistent between different calculations although different parton distribution function (PDF) sets were used for different predictions. The comparison of measured $t\overline{t}$ inclusive cross-sections at the Tevatron and at the LHC with the NNLO + NNLL theoretical predictions is shown in Figure 3. The agreement between predictions and measurements is excellent.

The top quark decays almost always into $t\to W+b$. The $t\overline{t}$ decay channels are thus characterized by decays of W boson which could be leptonic $W\to \ell \nu$ or hadronic $W\to q{\overline{q}}^{\prime }$. The $t\overline{t}$ decay chain is shown in Figure 4. There are three decay channels according to the number of charged leptons (the inclusion of the charge-conjugate mode is implied): the dilepton ($t\overline{t}\to {\ell }^{+}\nu b{\ell }^{-}\overline{\nu }\overline{b}$) (11%), lepton+jets ($\ell +$jets, $t\overline{t}\to {\ell }^{+}\nu bq{\overline{q}}^{\prime }\overline{b}$) (44%), and all-hadronic channel ($t\overline{t}\to q{\overline{q}}^{\prime }bq{\overline{q}}^{\prime }\overline{b}$) (44%). The quark is color particle which hadronize to create a spray of colorless final state particles (mostly hadrons) flying in about the same direction, a jet.

2.2. Charge Asymmetry in QED and EW Theory

The angular asymmetry in the differential cross-section of the pair production is the difference in production rates for a fermion and an antifermion flying along a given direction. In QED, it was noticed and calculated a long time ago for e.g., the $e^{+}{e}^{-}\to {\mu }^{+}{\mu }^{-}$ production [56]. At LO in QED, the ${\mu }^{+}{\mu }^{-}$ pair production is symmetric under the transformation ${\mu }^{+}\leftrightarrow {\mu }^{-}$, i.e., under the charge conjugation (C), with respect to the incoming $e^{+}$ and $e^{-}$ beams. The asymmetry is present at NLO due to the interference of processes that differ under C-conjugation, i.e., between the lowest order and two-photon box graphs and between C-odd and C-even breamshtrahlung diagrams, see Figure 5. The overall effect is that the positive muons ${\mu }^{+}$ fly a little bit more often in the same direction as incoming positive electrons $e^{+}$ while negative ${\mu }^{-}$ fly preferentially in the direction of negative $e^{-}$. It should be stressed that no parity-violating interactions are involved. The QED asymmetry prediction has been confirmed in the experiment [57], see Figure 6.

In the electroweak theory, the angular asymmetry is already predicted at LO due to the Z-boson axial-vector coupling to fermions [58]. It was precisely measured at LEP experiments for $e^{+}{e}^{-}\to q\overline{q},q=c,b$ reactions [59].

2.3. Charge Asymmetry in QCD

Similarly to QED, there is no charge asymmetry at LO in the QCD production of $q\overline{q}\to Q\overline{Q}$ while it is expected at NLO [60]. The asymmetry is thus of the order of ${\alpha }_s$ relative to the dominant production process. The corresponding QCD diagrams similar to QED diagrams contribute and again the asymmetry is induced through the interference between the amplitudes which are relatively odd under the $t\leftrightarrow \overline{t}$, i.e., the interference of box and LO Born diagrams and the interference of final-state and initial-state radiation diagrams, see Figure 7. The interference of virtual (box) diagrams and LO (Born) diagrams (Figure 7) contributes to a positive asymmetry while the interference of the diagrams with real-corrections has a negative asymmetry with the former to be dominant. The overall net effect is thus a positive asymmetry.

The asymmetry is present in the production for all quark pairs, not only top quark pairs. For light quarks $(u,d)$ when the initial and outgoing quark is the same, the t-channel $q\overline{q}\to q\overline{q}$ must be considered too [60]. The charge asymmetry in the $pp\to b\overline{b}$ production was measured at the LHC by the LHCb experiment [61], while the forward–backward asymmetry in the $p\overline{p}\to b\overline{b}$ production was measured at the Tevatron by the CDF experiment [62,63] and by the D0 experiment in the production of $B^{\pm }$ mesons [64]. At the Tevatron, the $b\overline{b}$ production is dominated by the $gg$ fusion unlike the top quark pair production due to the much lower b-quark mass. Therefore, the asymmetry is expected to be much smaller for $b\overline{b}$ compared to $t\overline{t}$. The $A_{\mathrm{FB}}$ measurement was performed at the CDF experiment at both low and high $m_{b\overline{b}}$, see Figure 8. Both CDF measurements and also LHCb measurement are consistent with the SM predictions, although typically with quite large uncertainties. The D0 measurement shows the discrepancy of about 3 SD between the measurement and the NLO QCD estimate from mc@nlo with a large theoretical uncertainty for the prediction which suggests that more precise prediction is needed to interpret this result.

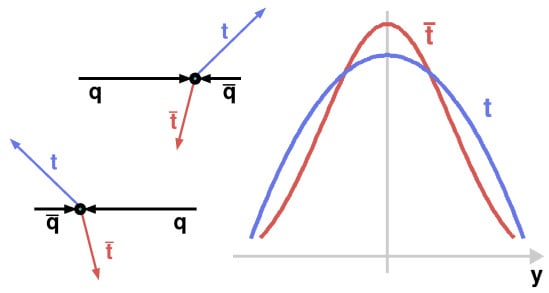
2.4. Top Quark Pair Charge Asymmetry

From the above description in Section 2.3, it follows that the $q\overline{q}\to t\overline{t}$ production is charge symmetric at LO and becomes asymmetric at NLO, i.e., the production of the top and antitop quark along a given direction is different. For the $gg\to t\overline{t}$ production, the initial state is symmetric and thus no asymmetry is predicted. For the $qg\left(\overline{q}g\right)\to t\overline{t}$ production, the asymmetry is also expected due to interference terms.

Moreover, there is an asymmetry already at LO in the EW production of the top quark pair $q\overline{q}\to {\gamma }^{*}/Z\to t\overline{t}$. In addition, QCD–EW interference terms contribute to the asymmetry. However, since the EW production of the $t\overline{t}$ pair is small compared to the QCD production, its contribution to the charge asymmetry is subdominant although important as it will be seen later.

The fraction of $gg\to t\overline{t}$ is increasing with increasing of the energy $\sqrt{s}$. Therefore, the overall asymmetry in $pp$ or $p\overline{p}$ collisions is decreasing as energy of collisions is increasing.

The $t\overline{t}$ charge asymmetry is quite different at the Tevatron and at the LHC. As mentioned above, $q\overline{q}$ is the dominant production process at the Tevatron, and it is $p\overline{p}$ collider, so the axis of initial quark largely coincides with the axis of initial proton. The asymmetry in $q\overline{q}\to t\overline{t}$ is thus largely preserved in $p\overline{p}\to t\overline{t}$ collisions. At the LHC, the dominant production process is $gg\to t\overline{t}$ which has no asymmetry. Therefore, the charge asymmetry is largely suppressed. Moreover, since $pp$ is a charge symmetric initial state, there is no overall charge asymmetry in $pp\to t\overline{t}$. However, the interacting initial quark is a valence quark, so it has in average a larger longitudinal momentum compared to an antiquark from the sea of quarks in the proton. Since top quarks fly a bit more often in the quarks direction, as a consequence, the top quarks will fly more in forward/backward direction compared to more central antitops.

2.5. Asymmetry Definitions

In general, it is important to state how the asymmetry is defined, in which frame and which observable is used for the definition.

As was already mentioned, the charge asymmetry present in a process $q\overline{q}\to t\overline{t}$ means that in the center-of-mass frame, the number of top quarks flying in a certain direction is different compared to the number of antitop quarks. Therefore, the asymmetry can be defined as

$$A_C^{t\overline{t}}\left(\cos \theta \right)=\frac{N_t\left(\cos \theta \right)-N_{\overline{t}}\left(\cos \theta \right)}{N_t\left(\cos \theta \right)+N_{\overline{t}}\left(\cos \theta \right)},$$

(1)

where $N_t\left(\cos \theta \right)$ and $N_{\overline{t}}\left(\cos \theta \right)$ are the number of top quarks and antitop quarks flying along $\cos \theta$ direction, where $\theta$ is computed with respect to the direction of the initial quark (and not the antiquark) in both cases. Since the asymmetry is defined as the ratio of two numbers, it is often quoted as a percentage. Such convention is adopted also in this article.

Assuming CP-invariance in strong interactions, $N_{\overline{t}}\left(\cos \theta \right)=N_t(-\cos \theta )$, and the charge asymmetry definition in Equation (1) can be rewritten using only the top quark without a need for the antitop quark:

$$A_C^{t\overline{t}}\left(\cos \theta \right)=\frac{N_t\left(\cos \theta \right)-N_t(-\cos \theta )}{N_t\left(\cos \theta \right)+N_t(-\cos \theta )}.$$

(2)

This can be then used to define the inclusive charge asymmetry by summing events from opposite hemispheres and it becomes forward–backward asymmetry:

$$A_{\mathrm{FB}}^{t\overline{t}}=\frac{N(\cos \theta >0)-N(\cos \theta <0)}{N(\cos \theta >0)+N(\cos \theta <0)},$$

(3)

where $N(\cos \theta >0)$ is the number of events with the top quark fulfilling condition $\cos \theta >0$.

The experiments at the Tevatron and at the LHC use a right-handed coordinate system with its origin at the nominal interaction point in the center of the detector and the z-axis along the beam pipe. At the Tevatron experiments, the z-axis points along the proton direction, while the y-axis points vertically upward and the x-axis points radially outwards. At LHC experiments, the x-axis points radially inward toward the center of the LHC, while the y-axis points vertically upward. Cylindrical coordinates $(r;\varphi )$ are used in the transverse plane, $\varphi$ being the azimuthal angle around the beam pipe. The polar angle is calculated with respect to z-axis. The pseudorapidity is defined in terms of the polar angle $\theta$ as $\eta =-\ln (\tan \theta /2)$, while the rapidity y is defined as $y=1/2\ln [(E+p_z)/(E-p_z)]$.

Instead of $\cos \theta$, other observables can be also used to define the asymmetry, for example the rapidity ($y_t$) or the pseudorapidity (${\eta }_t$) of the top quark, or $\Delta y_{t\overline{t}}=y_t-y_{\overline{t}}$. Clearly, the inclusive forward–backward asymmetry stays the same in $q\overline{q}$ center-of-mass frame independently of which variable is used.

Experimentally, the top and antitop quark are reconstructed using their decay products registered within a detector. There are numerous methods which have been developed for such task in the past [65,66,67,68,69,70,71,72,73,74]. For charge asymmetry measurements, it is needed to determine which of them is the top quark and the antitop quark. In the dilepton channel, it is relatively simple. The quark which decay has assigned the positive lepton is labeled as the top quark while the quark which has assigned negative lepton is labeled as the antitop quark. In the $\ell +$jets channel, there is just one final state lepton. After the $t\overline{t}$ reconstruction, the hadronic ($t_h$) and leptonic ($t_{\ell }$) top quark is labeled depending on which one has the hadronic and leptonic decay assigned, respectively. If the final state lepton has a positive electromagnetic charge, the leptonic top quark is labeled as the top quark and the hadronic top quark as the antitop quark. If the final state lepton has a negative charge, the leptonic top quark is labeled as the antitop quark.

Asymmetries can be measured also for decay products of top quarks. They will carry the information about a direction of flight of the top quarks due to the boost given by top quarks, but the direction will not be 100% correlated. Therefore, the asymmetry in decay products will be a little bit diluted. The potential decay products are W bosons, b quarks, light quarks, or charged leptons and neutrinos from W boson decay. The good candidates must have a well reconstructed direction of flight and an electromagnetic charge must be well measured for them. The light quarks are almost hopeless since they are reconstructed as jets which direction is not precisely measured and more importantly the charge determination is very hard. Better candidates would be b-jets since there are methods to measure the b-jet charge [75,76,77] but these are not very precise. The W boson is also not particularly good object because it can be reconstructed from either jets (hard to get a charge) or from the charged lepton and the neutrino (hard to precisely measure a direction). Therefore, the best candidates for measuring the asymmetry are charged leptons, since the reconstruction of both their charge and direction is excellent. This is also reason why the all-hadronic channel is not used for charge-asymmetry measurements.

Similarly as for the top quark, more variables can be used to define the leptonic asymmetry. Typically, only electrons and muons are used in measurements since the $\tau$ lepton reconstruction is more complicated. For these leptons, the pseudorapidity is used rather then the rapidity since it is easier to be measured. For practical purposes, the values are the same, given their large energies compared to their mass. Therefore, the $\eta$ of leptons or $\Delta \eta ={\eta }_{{\ell }^{+}}-{\eta }_{{\ell }^{-}}$ are used in the definition of the asymmetry.

2.5.1. Asymmetry Definitions for Tevatron

At the Tevatron $p\overline{p}$ collider, where $q\overline{q}\to t\overline{t}$ is the dominant production process, the valence quark from the proton interacts with the valence antiquark from the antiproton most of the time. Therefore, the charge and forward–backward asymmetry in $q\overline{q}\to t\overline{t}$ is mostly preserved in the $p\overline{p}\to t\overline{t}$ production although it is a little bit smaller due to a symmetric contribution of the $gg$ fusion.

The Tevatron measurements are performed in the laboratory frame ($p\overline{p}$ center-of-mass frame) or in the $t\overline{t}$ rest frame. There are advantages and disadvantages for both frames. The advantage of the $t\overline{t}$ rest frame is that the asymmetry is larger than the asymmetry in the laboratory frame. At the Tevatron in Run II, the laboratory frame asymmetry is diluted by 30% [42]. That is because in a given $q\overline{q}\to t\overline{t}$ interaction, the interacting quark and antiquark has in general a different longitudinal momentum in the laboratory frame which will give a boost to the $t\overline{t}$ system. It can then happen that even that the top quark flies in the forward direction in the $t\overline{t}$ rest frame, it will fly in the backward direction in the laboratory frame. For that reason, there is an advantage to use the $\Delta y_{t\overline{t}}$ variable. It is a Lorentz invariant, so it is independent of the $t\overline{t}$ longitudinal motion and it is simply related to the top quark rapidity in the $t\overline{t}$ rest frame: $y_t^{t\overline{t}}=1/2\Delta y$. The advantage of the laboratory frame is that it can be defined to rely only on the measured hadronically decaying top quark rapidity $y_{t_h}$ which has a much better resolution compared to the leptonically decaying top quark which includes only indirectly and partially (no z component) measured neutrino. Consequently, the statistical precision of $A_{\mathrm{FB}}$ is better in the $p\overline{p}$ frame.

The forward–backward asymmetry in the laboratory frame is usually defined using the rapidity of the top quark in the laboratory ($p\overline{p}$) frame, $y_t$:

$$A_{\mathrm{FB}}^{p\overline{p}}=\frac{N(y_t>0)-N(y_t<0)}{N(y_t>0)+N(y_t<0)}=\frac{N(-q_{\ell }y\left(t_h\right)>0)-N(-q_{\ell }y\left(t_h\right)<0)}{N(-q_{\ell }y\left(t_h\right)>0)+N(-q_{\ell }y\left(t_h\right)<0)},$$

(4)

where the rapidity of the hadronic top $y\left(t_h\right)$ is used. This has the advantage that it has a better resolution than $\Delta y$, but the disadvantage is that it measures the diluted laboratory frame asymmetry. Similarly, another variable can be used in the forward–backward asymmetry definition: $\cos \theta =q_{\ell }·\cos {\alpha }_p$ is used, where $\theta$ is the polar angle between the top quark and the proton beam while ${\alpha }_p$ is the polar angle between the hadronic top quark and the proton beam.

The $t\overline{t}$ rest frame asymmetry is defined using $\Delta y=y_t-y_{\overline{t}}$

$$A_{\mathrm{FB}}^{t\overline{t}}=\frac{N(\Delta y>0)-N(\Delta y<0)}{N(\Delta y>0)+N(\Delta y<0)}=\frac{N(q_{\ell }·(y_{t_{\ell }}-y_{t_h})>0)-N(q_{\ell }·(y_{t_{\ell }}-y_{t_h})<0)}{N(q_{\ell }·(y_{t_{\ell }}-y_{t_h})>0)+N(q_{\ell }·(y_{t_{\ell }}-y_{t_h})<0)},$$

(5)

where $q_{\ell }$ is the electric charge of the lepton, and $y_{t_{\ell }},y_{t_h}$ is the rapidity of the hadronically, leptonically decaying top, or antitop quark. The disadvantage is that $\Delta y$ has a worse resolution compared to $t_h$ since it combines the uncertainties of both quark reconstructions, including neutrino-related complications of the $t_{\ell }$ quark system.

For the leptonic defined asymmetry in the laboratory frame, the asymmetry is usually defined as:

$$A_{\mathrm{FB}}^{\ell }=\frac{N(q_{\ell }{\eta }_{\ell }>0)-N(q_{\ell }{\eta }_{\ell }<0)}{N(q_{\ell }{\eta }_{\ell }>0)+N(q_{\ell }{\eta }_{\ell }<0)}.$$

(6)

Similarly to the top quark asymmetry in the $t\overline{t}$ rest frame defined using $\Delta y$, the asymmetry in the dilepton channel can be defined this way:

$$A_{\mathrm{FB}}^{\ell \ell }=\frac{N(\Delta {\eta }_{\ell \ell }>0)-N(\Delta {\eta }_{\ell \ell }<0)}{N(\Delta {\eta }_{\ell \ell }>0)+N(\Delta {\eta }_{\ell \ell }<0)}=\frac{N({\eta }_{{\ell }^{+}}-{\eta }_{{\ell }^{-}}>0)-N({\eta }_{{\ell }^{+}}-{\eta }_{{\ell }^{-}}<0)}{N({\eta }_{{\ell }^{+}}-{\eta }_{{\ell }^{-}}>0)+N({\eta }_{{\ell }^{+}}-{\eta }_{{\ell }^{-}}<0)}.$$

(7)

The $A_{\mathrm{FB}}^{\ell }$ is related to $A_{\mathrm{FB}}^{pp}$ but the effect is smaller thanks to the dilution due to leptons not following the top quark direction precisely, which in turn is smaller than $A_{\mathrm{FB}}^{t\overline{t}}$. The $A_{\mathrm{FB}}^{\ell \ell }$ is related to $A_{\mathrm{FB}}^{t\overline{t}}$ but a bit smaller due to the same reason. Therefore, there is an advantage in using $A_{\mathrm{FB}}^{\ell \ell }$ since its value is not diluted by laboratory frame. However, the disadvantage is that $A_{\mathrm{FB}}^{\ell \ell }$ can be measured only in the dilepton channel, which has the smallest statistics.

2.5.2. Asymmetry Definitions for LHC

As it was already pointed out above, top quarks are more often produced in the forward/backward direction while antitops are produced more often in the central region. This can be explored to define the edge-central charge asymmetry, which will be called just simply the charge asymmetry in the following. Most often, the variable $\Delta \left|y\right|=|y_t|-|y_{\overline{t}}|$ is used to define the charge asymmetry:

$$A_{\mathrm{C}}=\frac{N(\Delta |y|>0)-N(\Delta |y|<0)}{N(\Delta |y|>0)+N(\Delta |y|<0)}.$$

(8)

For leptons, $\Delta \left|\eta \right|=|{\eta }_{\ell +}|-|{\eta }_{\ell -}|$ is used instead to define the dileptonic asymmetry:

$$A_{\mathrm{C}}^{\ell \ell }=\frac{N(\Delta |\eta |>0)-N(\Delta |\eta |<0)}{N(\Delta |\eta |>0)+N(\Delta |\eta |<0)}.$$

(9)

3. Theory Overview

The overview of theoretical predictions of the charge asymmetry in the top quark pair production at hadron colliders is presented. In the first part, the evolution of SM predictions is described while in the second part are mentioned various BSM models which could affect the $t\overline{t}$ charge asymmetry.

3.1. SM Predictions

First, it should be noted that two charge asymmetry definitions are used in theoretical calculations. In the first calculation (unexpanded), the most precise calculation available for the numerator and the denominator in the asymmetry definition is used. In such case, the denominator is effectively calculated at the higher order than the numerator since the asymmetry is non-zero starting only at NLO. For example, using the NLO calculation, the total cross-section (denominator) is at NLO while the numerator is effectively at LO. Therefore, it has been argued that it is better to define the charge asymmetry in a way that both the numerator and the denominator are at the same order, e.g., using the expansion in ${\alpha }_s$ (expanded definition). For example, use the LO cross-section in the denominator for the asymmetry calculation at NLO. In such way, uncalculated higher-order corrections should be at about the same level in both the numerator and the denominator. Using these two definitions provide quite different predictions for the asymmetry at NLO which is due to the large change between the LO and NLO cross-section. However, at NNLO, these definitions already provide very similar values, therefore it does not matter much which definition is used.

The initial attempt at predicting the forward–backward asymmetry in the pair production of top quarks was made more than 30 years ago even before the top quark was discovered [11]. The top quark mass used in the calculation was 45 GeV. In this calculation, only contributions from the initial and final state gluon radiation interference were considered, i.e., only the asymmetry in the $t\overline{t}$+jet process at LO was calculated. This was not the full NLO QCD correction to the inclusive $t\overline{t}$ asymmetry. This calculation required the introduction of cuts on the energy and the rapidity of gluons to avoid singularities. The predicted asymmetry was negative: up to about $-2\%$ for a given kinematic criteria on heavy quarks and gluons.

After the discovery of the top quark, but well before first measurements became available, the charge asymmetry was studied in a more detail using the full NLO QCD prediction [12,13]. This means including the interference terms of Born and virtual box corrections. It turned out that these contributions to the asymmetry were larger than the initial and final state radiation interference and they were in the opposite direction. The overall prediction for the forward–backward asymmetry thus changed the sign compared to the first partial NLO prediction and was positive. At the Tevatron and $\sqrt{s}=1.8$ TeV, the asymmetry was predicted to be up to 15% in $q\overline{q}\to t\overline{t}$ process in certain kinematic regions while the integrated forward–backward asymmetry was about 7–8% in the $t\overline{t}$ rest frame, see Figure 9, and about 4–5% in the $p\overline{p}$ laboratory frame.

As it was mentioned already, the asymmetry appears first at NLO in the inclusive $t\overline{t}$ production. This means that using the NLO QCD prediction, the asymmetry is known only at leading order accuracy since numerator has only the leading order contribution. In the $t\overline{t}$+jet production, the asymmetry is already present at LO QCD. Therefore, the NLO calculation of such process provides a true NLO prediction of the asymmetry. It was shown that NLO QCD contributions to the $t\overline{t}$+jet production provide very large corrections to the $t\overline{t}$+jet asymmetry which is then drastically reduced from about −8% at LO to about −2% at NLO for jet $p_{\mathrm{T}}>20$ GeV for the Tevatron Run II [14,15]. It was not clear at that time whether a similar shift would not happen for the inclusive $t\overline{t}$ prediction. Therefore, the NNLO prediction for the inclusive $t\overline{t}$ process was highly desirable.

It was believed for quite some time that EW corrections are small similarly as EW corrections to the inclusive cross-section are small due to ${\alpha }_s\gg \alpha$. It turned out this was not the case. It was found that EW corrections of the order $\mathcal{O}\left({\alpha }^2\right)$ and $\mathcal{O}\left(\alpha {\alpha }_s^2\right)$ have a surprisingly large effect. In general, about 20% of the enhancement with respect to the NLO QCD prediction is observed when including EW corrections [20,21,24,25]. Similarly, leptonic and dileptonic asymmetries were computed for the Tevatron and for the LHC too [23,24].

Furthermore, the higher-order corrections from the soft gluon QCD resummation have been studied at various accuracies. Initially, the soft gluon corrections at next-to-leading-logarithm (NLL) level were computed [16]. It was found that the asymmetry is stable with respect to these corrections: the inclusive asymmetry changed from $6.7\%$ to $6.6\%$ at the Tevatron Run II. Later on, the next-to-next-to-leading logarithm (NNLL) corrections were computed in [18,19]. Here, the change in the inclusive asymmetry is from $\left({7.4}_{-0.6}^{+0.7}\right)\%$ at NLO to $\left({7.3}_{-0.7}^{+1.1}\right)\%$ in Ref. [19], so again negligible change, while a modest change from $4.0\%$ to $5.2\%$ was found in Ref. [18].

Moreover, further understanding of soft-gluon emissions came from parton shower studies. It was shown that a coherent QCD radiation in the $t\overline{t}$ production leads to a forward–backward asymmetry that grows more negative with the increasing transverse momentum of the pair [78].

Finally, full NNLO QCD corrections were calculated [30]. These provided large, 27%, increase relative to the NLO QCD prediction for the inclusive asymmetry. The evolution of various calculations is shown in Figure 10. The EW contributions considered here are $\mathcal{O}\left({\alpha }_s^2\alpha \right)$ and $\mathcal{O}\left({\alpha }^2\right)$. The detailed studies of NNLO QCD predictions for various kinematic distributions have been presented in Ref. [31].

Later on, the ‘complete NLO’ corrections were added to the NNLO QCD prediction [32]. The complete NLO contributions include NLO QCD corrections at $\mathcal{O}\left({\alpha }_s^3\right)$, the NLO EW at $\mathcal{O}\left({\alpha }_s^2\alpha \right)$ as well as contributions at $\mathcal{O}\left({\alpha }_s{\alpha }^2\right)$ and $\mathcal{O}\left({\alpha }^3\right)$ together with LO corrections at $\mathcal{O}\left({\alpha }_s\alpha \right)$ and $\mathcal{O}\left({\alpha }^2\right)$. The comparison of various predictions of the charge asymmetry $A_{\mathrm{C}}$ with the experiments for the LHC at $\sqrt{s}=8$ TeV is shown in Figure 11.

Similarly as for the inclusive cross-section, the calculation of ${\mathrm{N}}^3$LO soft-gluon contributions together with the inclusion of above NNLO QCD calculation allowed to obtain the ${\mathrm{aN}}^3$LO prediction of $A_{\mathrm{FB}}$ [29]. The increase in the $A_{\mathrm{FB}}$ at the Tevatron due to ${\mathrm{N}}^3$LO soft-gluon contributions is about 5% compared to the pure NNLO QCD calculation.

As it was already mentioned above, the independent NNLO QCD prediction for the $t\overline{t}$ process has become available recently with the matrix program which provides fully differential $t\overline{t}$ predictions. The $\Delta y$ distribution was obtained and the forward–backward asymmetry for the Tevatron calculated for the following set of parameters: $m_t=172.5$ GeV, ${\mu }_R={\mu }_F=m_t$, NNPDF3.1 NNLO with ${\alpha }_s\left(M_Z\right)=0.118$ parton distribution function [79]. The result is: $A_{\mathrm{C}}^{t\overline{t}}=\left({7.4}_{-0.8}^{+0.3}\right)\%$. It should be noted that the uncertainty estimated here is only approximate since the matrix program provides only minimal and maximal deviations in the cross-section for scale variations for a given bin and the maximal potential difference to estimate the scale uncertainty was used. Nevertheless, the result is in excellent agreement with the above mentioned pure NNLO QCD prediction $\left({7.49}_{-0.86}^{+0.49}\right)\%$ from Ref. [30]. Similarly, the charge asymmetry at the LHC $\sqrt{s}=7$ TeV was calculated $A_{\mathrm{C}}=(0.95\pm 0.08)\%$.

The usual theoretical predictions set a renormalization and factorization scale to some value typical for the process, e.g., for the $t\overline{t}$ process it is typically a top quark mass. The uncertainty is then evaluated by changing the renormalization and factorization scale by a factor of two which is essentially just a consensus within the theoretical community, but has no deep foundation within the theory. The alternative calculation of the charge asymmetry is based on the Principle of Maximum Conformality (PMC) scale-setting approach where the renormalization scale is automatically determined and the corresponding uncertainty is essentially eliminated [80,81]. The PMC predictions were computed at NLO QCD with partial NNLO terms and also including NLO EW corrections (aNNLO + NLO EW). They were computed for the Tevatron and for the LHC [26,27,28]. The large difference between the PMC prediction and the conventional scale-setting NNLO prediction is seen for the Tevatron $A_{\mathrm{FB}}(m_{t\overline{t}}>450\mathrm{GeV})$ where the PMC predicts $A_{\mathrm{FB}}(m_{t\overline{t}}>450\mathrm{GeV})=29.9\%$ which is much larger compared to the NNLO prediction $A_{\mathrm{FB}}(m_{t\overline{t}}>450\mathrm{GeV})\approx 11\%$ [31]. It should be noted that the PMC method has a residual scale dependence due to the unknown perturbative terms which could be relatively large in the $t\overline{t}$ pair production [82] while the updates of the PMC method try to overcome this limitation [83,84].

When the direct theoretical prediction is not available, e.g., in a specific fiducial phase space, the charge asymmetry predictions are calculated using Monte Carlo (MC) programs or generators of particle collisions. Such programs have typically only NLO QCD corrections implemented, e.g., mc@nlo [85], powheg [86], or mcfm [87].

Summary of SM Predictions

The SM inclusive predictions at various orders, in various frames, and using different definitions are shown in

Table 2. The summary of Standard Model (SM) predictions for $t\overline{t}$ and leptonic forward–backward asymmetries at the Tevatron at various levels of the perturbation theory. Some predictions are in the laboratory frame (lab) while some are in the $t\overline{t}$ rest frame ($t\overline{t}$). Some of the predictions are using the unexpanded definition while the others use the expanded (ex) definition.

Prediction	${\mathit{A}}_{\mathbf{FB}}^{\mathit{t}\overline{\mathit{t}}}$ [%]	${\mathit{A}}_{\mathbf{FB}}^{\mathbf{\ell }}$ [%]	${\mathit{A}}_{\mathbf{FB}}^{\mathbf{\ell }\mathbf{\ell }}$ [%]
NLO QCD [12,13]	4–5 (lab)
NLO QCD [30]	${5.89}_{-1.40}^{+2.70}$ ($t\overline{t}$)
NLO QCD [30]	${7.34}_{-0.58}^{+0.68}$ ($t\overline{t}$, ex)
NLO QCD [23]	${4.9}_{-0.4}^{+0.5}$ (lab, ex)
NLO QCD [23]	${7.6}_{-0.5}^{+0.8}$ ($t\overline{t}$, ex)
NLOW [23]	${5.1}_{-0.3}^{+0.5}$ (lab, ex)
NLOW [23]	${8.0}_{-0.5}^{+0.7}$ ($t\overline{t}$, ex)
NLO QCD + EW [20,21,24,25]	5–6 (lab)
NLO QCD [24]		$3.1\pm 0.3$ (lab, ex)	$4.0\pm 0.4$ (ex)
NLO QCD + EW [24]	${5.77}_{-0.31}^{+0.40}$ (lab, ex)	$3.8\pm 0.3$ (lab, ex)	$4.8\pm 0.4$ (ex)
NLO QCD + EW [24]	${8.75}_{-0.48}^{+0.58}$ ($t\overline{t}$, ex)
NLO QCD + NNLL [30]	${7.24}_{-0.67}^{+1.04}$ ($t\overline{t}$, ex)
NNLO [30]	${7.49}_{-0.86}^{+0.49}$ ($t\overline{t}$)
NNLO(matrix)	${7.4}_{-0.8}^{+0.3}$ ($t\overline{t}$)
NNLO [30]	${8.28}_{-0.26}^{+0.27}$ ($t\overline{t}$, ex)
aN${}^3$LO QCD [29]	$8.7\pm 0.2$ ($t\overline{t}$, ex)
NNLO QCD + EW [30]	$9.5\pm 0.7$ ($t\overline{t}$, ex)
aN${}^3$LO QCD + EW [29]	$10.0\pm 0.6$ ($t\overline{t}$, ex)
PMC [28]	$12.5$ ($t\overline{t}$, ex)

and

Table 3. The summary of SM predictions for charge asymmetry at various levels of perturbation theory at the LHC for different center-of-mass energies. All of these predictions are in the laboratory frame. Some of the predictions are using the unexpanded definition while the others use the expanded (ex) definition.

Prediction	$\sqrt{\mathit{s}}$ [TeV]	${\mathit{A}}_{\mathbf{C}}^{\mathit{t}\overline{\mathit{t}}}$ [%]	${\mathit{A}}_{\mathbf{C}}^{\mathbf{\ell }\mathbf{\ell }}$ [%]
NLO [24]	7	$1.07\pm 0.04$ (ex)	$0.61\pm 0.03$
NLO+EW [24]	7	$1.23\pm 0.05$ (ex)	$0.70\pm 0.03$
NLO+EW [21]	7	$1.15\pm 0.06$ (ex)
NLO+EW ($\Delta \left|\eta \right|$) [21]	7	$1.36\pm 0.08$ (ex)
NNLO (MATRIX)	7	$0.95\pm 0.08$
PMC [27]	7	${1.15}_{-0.03}^{+0.01}$ (ex)
NLO [24]	8	$0.96\pm 0.04$ (ex)	$0.55\pm 0.03$
NLO+EW [24]	8	$1.11\pm 0.04$ (ex)	$0.64\pm 0.03$
NLO [32]	8	${0.73}_{-0.13}^{+0.23}$
NLO [32]	8	${0.96}_{-0.09}^{+0.11}$ (ex)
NLO+EW [32]	8	${0.86}_{-0.14}^{+0.25}$
NLO+EW [32]	8	${1.13}_{-0.08}^{+0.10}$ (ex)
NNLO [32]	8	${0.83}_{-0.06}^{+0.03}$
NNLO [32]	8	${0.85}_{-0.04}^{+0.02}$ (ex)
NNLO+EW [32]	8	${0.95}_{-0.07}^{+0.05}$
NNLO+EW [32]	8	${0.97}_{-0.03}^{+0.02}$ (ex)
PMC [27]	8	${1.03}_{-0.00}^{+0.01}$ (ex)
NLO+EW [25]	13	${0.75}_{-0.05}^{+0.04}$ (ex)	$0.55\pm 0.03$ (ex)
NNLO+EW [88]	13	${0.64}_{-0.05}^{+0.06}$
NLO [24]	14	$0.58\pm 0.03$ (ex)	$0.36\pm 0.02$ (ex)
NLO+EW [24,25]	14	${0.66}_{-0.04}^{+0.05}$ (ex)	$0.43\pm 0.02$ (ex)
PMC [27]	14	${0.62}_{-0.02}^{+0.00}$(ex)

. At the Tevatron, the predictions have increased significantly by almost factor of two when going from NLO in the laboratory frame to NNLO QCD + NLO EW in the $t\overline{t}$ frame. At the LHC, the charge asymmetry decreases with the increase of the energy of interactions due to the increase of the symmetric $gg$ production process fraction.

It was realized already very early in the initial predictions [11,12,13,60] that the charge asymmetry depends on the initial/final state gluon radiation due to the interference of these diagrams contributing to the asymmetry. It is therefore expected the asymmetry depends on $p_{\mathrm{T}}$ of the final-state jet which is related to $p_{\mathrm{T},t\overline{t}}$ (the size of $p_{\mathrm{T}}$ of the jet will be the same as $p_{\mathrm{T}}$ of $t\overline{t}$, the direction will be opposite in the transverse plane). The contribution from such interference to the asymmetry is negative, so the larger $p_{\mathrm{T}}$ the more negative asymmetry is expected. The variable $|y_{t\overline{t}}|$ is sensitive to the ratio of the contributions from the $q\overline{q}$ and $gg$ initial states. The charge-symmetric $gg$ initial state produces more central $t\overline{t}$ events while $q\overline{q}$ contributes more in the forward direction. Therefore, it is expected the asymmetry will rise with the increasing value of $\Delta y$. The charge asymmetry is expected to also rise for the $m_{t\overline{t}}$ variable since the $q\overline{q}$ initial state is enhanced for larger values of this variable. Finally, the charge asymmetry is expected to rise steeply for high boost of the $t\overline{t}$ system along the longitudinal axis [33]. It is due to the much higher average momentum fractions for quarks than for antiquarks in $pp$ collisions. Requiring the high boost of $t\overline{t}$ system thus increases the $q\overline{q}$ fraction and consequently also the charge asymmetry. As a consequence, the predictions of differential asymmetries as a function of the above mentioned variables were calculated (and also measured), see Figure 12.

3.2. BSM Models

After CDF claimed an evidence for 3 SD deviation from the SM prediction at that time in one of their $A_{\mathrm{FB}}$ measurements (for large $m_{t\overline{t}}>450$ GeV), there have been lots of new physics BSM models proposed to explain such measurement, see Refs. [33,34,35,36,37,38,39,45,46].

The BSM models also give us a strong reason to measure all different combinations of asymmetries, e.g., $A_{\mathrm{C}}$, $A_{\mathrm{FB}}$, $A_{\mathrm{FB}}^{\ell }$. While in the SM, the $A_{\mathrm{FB}}$ and $A_{\mathrm{C}}$ have the same underlying cause and there is a specific relation between $A_{\mathrm{FB}}$ and $A_{\mathrm{C}}$, this relation can be largely changed in BSM models. It was shown that using for example the axigluon model, it is possible to obtain a negative $A_{\mathrm{C}}$ at the LHC for positive $A_{\mathrm{FB}}$ asymmetry at the Tevatron [36,37]. The correlation between $A_{\mathrm{FB}}$ and $A_{\mathrm{FB}}^{\ell }$ is given in the SM. It is due to the fact that there is about zero top quark polarization in $t\overline{t}$ events, i.e., there is an equal number of positive and negative helicity top quarks produced. Models with different top quark polarization could change the $A_{\mathrm{FB}}$ and $A_{\mathrm{FB}}^{\ell }$ relations in both directions. This was studied in Refs. [46,89] for axigluon and $W^{\prime }$ models, where it was shown that for the same $A_{\mathrm{FB}}$ there was different $A_{\mathrm{FB}}^{\ell }$ predicted.

There are a few models which can change the charge asymmetry [34,35]:

• axigluons (a color octet vector ${\mathcal{G}}_{\mu }$): massive gluons with axial currents (’axigluons’). Similarly to EW theory with the axial current which has a massless photon and a massive Z boson and there is an asymmetry due to the $\gamma -Z$ interference already at LO, the interference between gluon and axigluon in the s-channel mediating $q\overline{q}\to t\overline{t}$ process produces a charge asymmetry;
• $Z^{\prime }$ (a neutral vector boson ${\mathcal{B}}_{\mu }$): a flavour violating Z’ exchanged in the t-channel in $u\overline{u}\to t\overline{t}$;
• $W^{\prime }$ (a charged boson ${\mathcal{B}}_{\mu }^1$): a boson with right-handed couplings exchanged in the t-channel in $d\overline{d}\to t\overline{t}$;
• ${\omega }^4$ (color-triplet scalar): a color triplet with right-handed flavour-violating $tu$ couplings exchanged in the u-channel in $u\overline{u}\to t\overline{t}$;
• ${\Omega }^4$ (color-sextet scalar): similarly as above, a color sextet with right-handed flavour-violating $t-u$ couplings exchanged in the u-channel. There may be diagonal $uu$, $tt$ couplings, in contrast with the ${\omega }^4$ triplet above;
• $\varphi$ (scalar isodoublet): a color-singlet Higgs-like isodoublet, which contains neutral and charged scalars, coupling the top quark to the first generation and exchanged in the t-channel.

The diagrams showing potential contributions from BSM models are shown in Figure 13. The potential values of the charge asymmetry at the LHC and the forward–backward asymmetry at the Tevatron for the above models with various parameters are shown in Figure 14.

4. Experimental Measurements

The measurements performed at the Tevatron and at the LHC are reviewed in this section. At the Tevatron, being the $p\overline{p}$ collider, it was possible to measure forward–backward asymmetry. At the LHC, being $pp$ collider, the edge–central charge asymmetry $A_{\mathrm{C}}$ has been measured.

All $A_{\mathrm{FB}}$ measurements at the Tevatron were performed in Run II data taking period. Two general-purpose experiments were collecting the data: CDF [92] and D0 [93]. The charge asymmetry measurements at the LHC have been performed in both the Run 1 and Run 2 data taking periods by both general-purpose experiments, ATLAS [94] and the Compact Muon Solenoid (CMS) [95].

At the LHC, there are more experiments running. The LHCb experiment, designed to study b-quark interactions, is one of them and it also observed the top quark [96]. However, up to now, only cross-section measurements of the top quark have been performed at the LHCb and no $t\overline{t}$ charge asymmetry related studies.

As it was mentioned above, it is important to measure all possible combinations of the asymmetries, i.e., measure both $A_{\mathrm{FB}}$ at the Tevatron and $A_{\mathrm{C}}$ at the LHC and also both $t\overline{t}$ and leptonic asymmetries, since the relation between them is model dependent. Experiments at the Tevatron and at the LHC therefore performed full set of these measurements where possible, in both $\ell +$jets and dilepton channels.

Most of the measurements follow this typical procedure. First, selection criteria are applied to select the sample which is enhanced in $t\overline{t}$ events. The backgrounds are estimated using MC or data driven methods. For the $t\overline{t}$ asymmetry, the kinematic reconstruction of top and antitop quark 4-momenta is performed using the measured top quark decay products. For lepton-based asymmetries, this is not needed. The kinematic variable which is used to define the asymmetry is calculated. At the Tevatron, this is mostly $\Delta y$ (for the top quark asymmetry), ${\eta }_{\ell }$ (for the lepton-based asymmetry), and $\Delta {\eta }_{\ell \ell }$ (for the dileptonic asymmetry). At the LHC, this is mostly $\Delta \left|y\right|$ (for the top quark asymmetry) and $\Delta \left|\eta \right|$ (for the dileptonic asymmetry). The kinematic distribution of the observable of interest is plotted for data, see e.g., Figure 15a. This corresponds to ’reco level’ before the background subtraction. Subsequently, the expected distribution for the background process is subtracted from the distribution in data, corresponding to ’reco level’ after background subtraction, see e.g., Figure 15b. The resulting distribution is assumed to correspond to the $t\overline{t}$ distribution after the reconstruction and event selection.

The ‘reco level’ has a disadvantage that it includes detector resolution and acceptance effects, so such results can be only compared to MC generator predictions which pass detector simulation and reconstruction and can not be directly compared to results from other experiments nor to the direct theoretical predictions. In order to be able to compare to the latest, most precise predictions, such distribution needs to be corrected for detector resolution effects and for the event selection acceptance and inefficiency. This correction is typically performed by the procedure of unfolding. Removing the detector effects brings the distributions to the ‘parton’ or ‘particle’ level, see e.g., Figure 15c. When extrapolating to the full phase space and to the level of top quarks, it is called a parton level. This allows to compare experimental results directly to theoretical calculations or to other experiments. Most of the results from the experiments are at parton level and it will be not mentioned unless it is otherwise. When unfolding to the level of final state stable particles and typically requiring some fiducial cuts on final state particles such as $p_{\mathrm{T}}$ or $\left|\eta \right|$ which are similar to event selection criteria, it is called a particle level. The advantage of the ‘particle fiducial level’ is that there is a much smaller degree of the extrapolation to an unmeasured phase-space compared to the parton level and consequently modeling uncertainties are typically smaller. Moreover, it is less ambiguous than the parton level, since the ‘top quark’ definition can differ between different MC generators which are necessary when performing the unfolding. However, not many predictions are available at such level.

The asymmetry can be calculated at each level by counting the events at positive and negative side of the x-axis with the statistical uncertainty properly calculated taking into account possible correlations between the bins which arise due to e.g., systematic uncertainties of the unfolding procedure. Since the asymmetry is expected to depend on a few different observables within the SM and even differently in BSM models, the experiments also performed lots of differential measurements of the asymmetry mostly as a function of $m_{t\overline{t}}$, $p_{\mathrm{T},t\overline{t}}$, $\Delta y_{t\overline{t}}$, and ${\beta }_{z,t\overline{t}}$.

There are also some measurements which use different methods to obtain the asymmetry and these will be mentioned later when describing a specific measurement.

4.1. Forward–Backward Asymmetry Measurements at the Tevatron

The CDF and D0 experiments started to perform measurements of $A_{\mathrm{FB}}$ from the beginning of Run II. The initial measurements at the Tevatron were performed in the $\ell +$jets channel with about 10–20% of eventual Run II statistics [40,41]. The next set of measurements were performed with about half of full Run II statistics by both CDF [42] and D0 [43,44]. These already included also the measurement of leptonic asymmetries.

Both CDF and D0 collaborations performed the full set of measurements in both $\ell +$jets and dilepton channels with full Run II statistics [72,97,98,99,100,101,102,103]. Moreover, there was performed the combination of the CDF and D0 measurements [49].

All these measurements will be described in the following.

4.1.1. Initial Measurements

The first measurement related to the charge asymmetry in the top quark pair production was performed by the D0 experiment using $0.9{\mathrm{fb}}^{-1}$ of the integrated luminosity [40]. It was performed only at reco level in the $t\overline{t}$ rest frame using $\Delta y$. The inclusive asymmetry was not measured, only the $A_{\mathrm{FB}}$ as a function of the number of reconstructed jets. The measured values are listed in

Table 4. The mc@nlo predictions and measured forward–backward asymmetries at reco level as a function of the number of jets in the D0 measurement using $0.9{\mathrm{fb}}^{-1}$ [40].

Number of Jets	${\mathit{A}}_{\mathbf{FB}}^{\mathit{t}\overline{\mathit{t}}}$(mc@nlo) [%]	${\mathit{A}}_{\mathbf{FB}}^{\mathit{t}\overline{\mathit{t}}}$(data) [%]
≥4	$0.8\pm 1.0$	$12\pm 8(\mathrm{stat}.)\pm 1(\mathrm{syst}.)$
4	$2.3\pm 1.0$	$19\pm 9(\mathrm{stat}.)\pm 2(\mathrm{syst}.)$
≥5	$-4.9\pm 1.1$	$-{16}_{-17}^{+15}(\mathrm{stat}.)\pm 3(\mathrm{syst}.)$

together with predictions from mc@nlo generator where events passed the full simulation and reconstruction as data.

In the CDF measurement using $1.9{\mathrm{fb}}^{-1}$ [41], the acceptance and reconstruction effects were already corrected for and parton-level asymmetries were measured. The asymmetry was measured using two observables, $-q_{\ell }·\cos {\theta }_p$ and $\Delta y$, which measured the asymmetry in $p\overline{p}$ and $t\overline{t}$ rest frame, respectively. Measured distributions for these variables are shown in Figure 16. Inclusive asymmetries were measured to be $A_{\mathrm{FB}}^{p\overline{p}}=(17\pm 7(\mathrm{stat}.)\pm 4(\mathrm{syst}.))\%=(17\pm 8)\%$ in the $p\overline{p}$ frame and $A_{\mathrm{FB}}^{t\overline{t}}=(24\pm 13(\mathrm{stat}.)\pm 4(\mathrm{syst}.))\%=(24\pm 14)\%$ in the $t\overline{t}$ frame. These asymmetries were still consistent (within 2 SD) with at that time available NLO QCD prediction of about 5% in $p\overline{p}$ frame and about 30% higher prediction in $t\overline{t}$ frame. Asymmetries were also measured as a function of the number of jets at reco level, similarly as in the above D0 measurement.

To summarize these initial Tevatron measurements: only the $t\overline{t}$ forward–backward asymmetry was measured in the $\ell +$jets channel only. Both experiments showed larger than at that time and even presently predicted asymmetries although they were really limited by a small data sample and so still consistent with the predictions. The CDF results pointed to the expected frame dependence. The measurement as a function of the number of jets in both CDF and D0 pointed to the expected trend of decreasing asymmetry with the increase in the number of jets.

4.1.2. Measurements with Half of Run II Statistics

Both CDF and D0 performed the measurement of the $t\overline{t}$ asymmetry with about a half of the full Run II statistics. CDF performed only the $t\overline{t}$ asymmetry measurement in the $\ell +$jets channel while D0 performed the measurement of $A_{\mathrm{FB}}^{t\overline{t}}$, $A_{\mathrm{FB}}^{\ell }$, and $A_{\mathrm{FB}}^{\ell \ell }$ in the $\ell +$jets and dilepton channel.

The CDF measurement [42] was performed with $5.3{\mathrm{fb}}^{-1}$ in both laboratory and $t\overline{t}$ rest frames using $y_t$ and $\Delta y$, respectively. The distributions at the reco level are shown in Figure 17 where data are compared to mc@nlo generator predictions. The inclusive measurements at different levels are summarized in

Table 5. The summary of inclusive asymmetries in $t\overline{t}$ and $p\overline{p}$ rest frames at the reco level with and without including the background, and at the parton level corresponding to the CDF measurement using $5.3{\mathrm{fb}}^{-1}$. Uncertainties include statistical, systematic, and theoretical uncertainties [42].

Sample	Level	${\mathit{A}}_{\mathbf{FB}}^{\mathit{t}\overline{\mathit{t}}}$ [%]	${\mathit{A}}_{\mathbf{FB}}^{\mathit{p}\overline{\mathit{p}}}$ [%]
data	reco (with background)	$5.7\pm 2.8$	$7.3\pm 2.8$
mc@nlo	reco (with background)	$1.7\pm 0.4$	$0.1\pm 0.3$
data	reco (without background)	$7.5\pm 3.7$	$11.0\pm 3.9$
mc@nlo	reco (without background)	$2.4\pm 0.5$	$1.8\pm 0.5$
data	parton	$15.8\pm 7.4$	$15.0\pm 5.5$
mcfm	parton	$5.8\pm 0.9$	$3.8\pm 0.6$

. The measured $A_{\mathrm{FB}}^{p\overline{p}}$ asymmetry exceeds the mc@nlo prediction by more than two standard deviations at all correction levels. The $A_{\mathrm{FB}}^{t\overline{t}}$ asymmetries are similar in a magnitude to the $A_{\mathrm{FB}}^{p\overline{p}}$ but they are less significant because of the larger relative uncertainties. The $A_{\mathrm{FB}}^{t\overline{t}}$ is also measured as a function of $\Delta y$ and $m_{t\overline{t}}$ in two bins, see Figure 18. At high values of $\Delta y$ and $m_{t\overline{t}}$, the asymmetries are higher than predictions available at that time. While the difference was less than 2 SD for high $\Delta y$, it was about 3.4 SD for high $m_{t\overline{t}}$ bin ($(47.5\pm 10.1(\mathrm{stat}.)\pm 4.9(\mathrm{syst}.))\%=(47.5\pm 11.4)\%$ in data, while $(8.8\pm 1.3)\%$ for NLO QCD in mcfm). It should be noted that in this measurement, CDF also tested the CP-invariance assumption by calculating charge separated asymmetries. The asymmetries in both laboratory and $t\overline{t}$ rest frame are equal and opposite within uncertainties, as expected.

D0 performed a similar measurement in the $\ell +$jets channel using $5.4{\mathrm{fb}}^{-1}$ [43]. Both $t\overline{t}$ and leptonic asymmetries are measured using $\Delta y$ and $q·y_{\ell }$ distributions, respectively, see Figure 19. The measured inclusive asymmetry is $A_{\mathrm{FB}}^{t\overline{t}}=(19.6\pm 6.5)\%$ and $A_{\mathrm{FB}}^{\ell }=(15.2\pm 4.0)\%$ which disagree with the NLO QCD prediction from mc@nlo ($A_{\mathrm{FB}}=(5.0\pm 0.1)\%$ and $A_{\mathrm{FB}}^{\ell }=(2.1\pm 0.1)\%$) by about 2.4 SD and 3.2 SD, respectively. The differential $t\overline{t}$ asymmetry measured as a function of $m_{t\overline{t}}$ and $\Delta y$ only at the reco level is summarized in

Table 6. The reco level $A_{\mathrm{FB}}^{t\overline{t}}$ by subsample in the D0 $\ell +$jets measurement using $5.4{\mathrm{fb}}^{-1}$ [43].

Subsample	${\mathit{A}}_{\mathbf{FB}}^{\mathit{t}\overline{\mathit{t}}}$ (Data) [%]	${\mathit{A}}_{\mathbf{FB}}^{\mathit{t}\overline{\mathit{t}}}$ (mc@nlo) [%]
$m_{t\overline{t}}<450\mathrm{Ge}\mathrm{V}$	$7.8\pm 4.8$	$1.3\pm 0.6$
$m_{t\overline{t}}>450\mathrm{Ge}\mathrm{V}$	$11.5\pm 6.0$	$4.3\pm 1.3$
$|\Delta y|<1.0$	$6.1\pm 4.1$	$1.4\pm 0.6$
$|\Delta y|>1.0$	$21.3\pm 9.7$	$6.3\pm 1.6$

.

In the dilepton channel, the leptonic and dileptonic asymmetry is measured by D0 using $5.4{\mathrm{fb}}^{-1}$ [44]. The leptonic asymmetry is measured to be $A_{\mathrm{FB}}^{\ell }=(5.8\pm 5.1(\mathrm{stat}.)\pm 1.3(\mathrm{syst}.))\%$ while the dileptonic asymmetry is $A_{\mathrm{FB}}^{\ell \ell }=(5.3\pm 7.9(\mathrm{stat}.)\pm 2.9(\mathrm{syst}.))\%$. The combination with the result in the $\ell +$jets channel yields $A_{\mathrm{FB}}^{\ell }=(11.8\pm 3.2)\%$.

To summarize mid-term measurements: these measurements were performed in both $\ell +$jet and dilepton channels and both $t\overline{t}$ and leptonic based asymmetries were measured. Moreover, the $t\overline{t}$ asymmetry is measured as a function of $m_{t\overline{t}}$ and $\Delta y$. The inclusive $t\overline{t}$ asymmetry is observed by both CDF and D0 to be larger than the predictions available at that time by 1.4–2.2 SD depending on the experiment, the frame, and the prediction. The $t\overline{t}$ asymmetry at high $y_{t\overline{t}}$ and $m_{t\overline{t}}$ region was measured by CDF to be larger than predicted by up to 3.4 SD at high $m_{t\overline{t}}$ values while D0 did not see any significant disagreement. The leptonic asymmetry was measured only by D0 and was again higher than the prediction available at that time, mostly for the $\ell +$jets channel where the deviation is in between 2.6 and 3.3 SD depending on the prediction ( $(2.1\pm 0.1)\%$ in mc@nlo and $(4.7\pm 0.1)\%$ in mc@nlo + NLO EW corrections, see [43,44]). Moreover, $A_{\mathrm{FB}}^{\ell \ell }$ was also measured to be consistent with the prediction, but with significant uncertainties. The dominant uncertainty in these measurements was still the statistical uncertainty. Although the amount of data analyzed increased by factor 3–6, the systematic uncertainties were largely improved by about factor of two. It was clear that the progress on both the experimental side, to improve the statistical precision, and on the theory side, to make more reliable uncertainties, was needed.

4.1.3. Measurements with Full Statistics

The measurements with the full Tevatron Run II statistics were performed by CDF and D0 in both $\ell +$jets and dilepton channels and for the whole set of $A_{\mathrm{FB}}^{t\overline{t}}$, $A_{\mathrm{FB}}^{\ell }$, and $A_{\mathrm{FB}}^{\ell \ell }$ asymmetries.

CDF measured $t\overline{t}$ asymmetry in the $\ell +$jets channel using $9.4{\mathrm{fb}}^{-1}$ [97] and in the dilepton channel using $9.1{\mathrm{fb}}^{-1}$ [72]. The $\Delta y$ distribution in the $\ell +$jets channel is plotted in Figure 15 where also the inclusive asymmetry measurements are summarized at various levels. The measured inclusive asymmetry in the dilepton channel is $A_{\mathrm{FB}}^{t\overline{t}}=(12\pm 11(\mathrm{stat}.)\pm 7(\mathrm{syst}.))\%=(12\pm 13)\%$. The asymmetry is also measured as a function of $|\Delta y|$, and $m_{t\overline{t}}$ in the $\ell +$jets channel, see Figure 20. The dependencies on these kinematic variables are linear and the slope is higher by 2.8 SD and 2.4 SD than expected from the NLO QCD prediction by powheg. In the dilepton channel, only the differential asymmetry as a function of $\Delta y$ is measured in two bins ($A_{\mathrm{FB}}^{t\overline{t}}\left(\right|\Delta y<0.5\left|\right)=(12\pm 3.9)\%$ and $A_{\mathrm{FB}}^{t\overline{t}}\left(\right|\Delta y>0.5\left|\right)=(13\pm 17)\%$).

D0 measured the $t\overline{t}$ asymmetry in the $\ell +$jets channel using full Run II statistics of $9.7{\mathrm{fb}}^{-1}$ [102]. The inclusive asymmetry is measured $A_{\mathrm{FB}}^{t\overline{t}}=(10.6\pm 3.0)\%$. The dependence of the asymmetry on the $|\Delta y|$ and $m_{t\overline{t}}$ was also measured, see Figure 21. The linear fit is performed to these dependencies and the slope is measured to be $15.4\pm 4.3$ and $3.9\pm 4.4\times {10}^{-4}$, respectively.

In the dilepton channel, D0 measured simultaneously $A_{\mathrm{FB}}^{t\overline{t}}$ and the top quark polarization using $9.7{\mathrm{fb}}^{-1}$ [103]. If the top quark polarization is fixed to its expected SM value, the measured value of asymmetry is $A_{\mathrm{FB}}^{t\overline{t}}=(17.5\pm 5.6(\mathrm{stat}.)\pm 3.1(\mathrm{syst}.))\%$.

In order to study the source of unexpectedly large forward–backward asymmetry in more detail, CDF measured the cross-section as a function of the top quark production angle $\mathrm{d}\sigma /\mathrm{d}\cos {\theta }_t$ [98]. The shape of such differential distribution is characterized by Legender polynomials and the Legender moments $a_1-a_8$ are measured. For the $q\overline{q}\to t\overline{t}$ process at LO, it is expected that there are non-zero $a_0$ and $a_2$ moments. $gg\to t\overline{t}$ is expected to add only small contributions to all even-degree Legender moments. The measured Legender moments $a_1-a_4$ are shown in Figure 22, the remaining ones are consistent with zero within large uncertainties. A good agreement within the uncertainties with the NLO SM prediction is observed for the moments $a_2-a_8$, but $a_1$ showed an excess with respect to the prediction: $a_1=0.40\pm 0.12$ vs. NLO SM: ${0.15}_{-0.03}^{+0.07}$. It means the excess was observed in the differential cross-section in the term linear in $\cos \theta$.

The leptonic measurements have been performed in both $\ell +$jets and dilepton channels by both CDF and D0 experiments. In the $\ell +$jets channel, the leptonic asymmetry is measured by CDF using $9.4{\mathrm{fb}}^{-1}$ [99] while D0 uses $9.7{\mathrm{fb}}^{-1}$ [104]. Both CDF and D0 measure the single-leptonic asymmetry using the charge-weighted rapidity $q{y}_{\ell }$. The CDF measurement separates the rapidity distribution into symmetric part, which is largely independent on the model, and the antisymmetric part which encapsulates the possible variation between the modes. The inclusive asymmetry is measured to be $A_{\mathrm{FB}}^{\ell }=(10.5\pm 2.4{(\mathrm{stat}.)}_{-1.7}^{+2.2}(\mathrm{syst}.))\%=\left({10.5}_{-2.9}^{+3.2}\right)\%$ which is 2.3 SD away from the NLO QCD + NLO EW prediction ($(3.8\pm 0.3)\%$). D0 measured the asymmetry in restricted region of $|y_{\ell }|<1.5$: $A_{\mathrm{FB}}^{\ell }=\left({4.2}_{-3.0}^{+2.9}\right)\%$. The asymmetry is measured also as a function of $p_{\mathrm{T}}$ of lepton and $|y_t|$.

In the dilepton channel, both CDF using $9.1{\mathrm{fb}}^{-1}$ [100] and D0 using $9.7{\mathrm{fb}}^{-1}$ [101] measure both single-lepton and dilepton asymmetries using $q{\eta }_{\ell }$ and $\Delta {\eta }_{\ell }$, respectively. In the CDF measurement, similarly to previous measurement in the $\ell +$jets channel, the pseudorapidity distributions are splitted into symmetric and antisymmetric parts. The results are $A_{\mathrm{FB}}^{\ell }=(7.2\pm 5.2(\mathrm{stat}.)\pm 3.0(\mathrm{syst}.))\%=(7.2\pm 6.0)\%$ and $A_{\mathrm{FB}}^{\ell \ell }=(7.6\pm 7.2(\mathrm{stat}.)\pm 3.9(\mathrm{syst}.))\%=(7.6\pm 8.2)\%$. D0 measured the inclusive asymmetries using the distributions shown in Figure 23. The measured values are $A_{\mathrm{FB}}^{\ell }=(4.4\pm 3.7(\mathrm{stat}.)\pm 1.1(\mathrm{syst}.))\%$ and $A_{\mathrm{FB}}^{\ell \ell }=(12.3\pm 5.4(\mathrm{stat}.)\pm 1.5(\mathrm{syst}.))\%$. The dependence of asymmetries on $|q{\eta }_{\ell }|$ and $|\Delta {\eta }_{\ell }|$ is also measured but only in the fiducial parton level phase-space (leptons must have $\left|\eta \right|<2$ and $|\Delta \eta |<2.4$).

4.1.4. Full Dataset Combinations

Both CDF and D0 performed individual combinations of their $t\overline{t}$ and single-lepton asymmetry measurements from both $\ell +$jets and dilepton channels using the full Run II data statistics of the actual experiment [72,100,103,104]. Moreover, they performed together the Tevatron combinations of all their results from both channels [49].

CDF combined inclusive $t\overline{t}$ asymmetry is $A_{\mathrm{FB}}^{t\overline{t}}=(16.0\pm 4.5(\mathrm{stat}.+\mathrm{syst}.))\%$ while the D0 combination is $A_{\mathrm{FB}}^{t\overline{t}}=(11.8\pm 2.5(\mathrm{stat}.)\pm 1.3(\mathrm{syst}.))\%$. The combined single-leptonic asymmetry at CDF is $A_{\mathrm{FB}}^{\ell }=\left({9.0}_{-2.6}^{+2.8}(\mathrm{stat}.+\mathrm{syst}.)\right)\%$ while the D0 combination is $(4.7\pm 2.3(\mathrm{stat}.)\pm 1.5(\mathrm{syst}.))\%$. For the differential $A_{\mathrm{FB}}^{t\overline{t}}$ as a function of $\Delta y$, rather then combining the data, the combined fit of the slope to both CDF $\ell +$jets and dilepton data was performed. The result is $\alpha =0.227\pm 0.057$ which is 2 SD larger than the NNLO QCD prediction of ${0.114}_{-0.012}^{+0.006}$ [31].

The Tevatron combination of the CDF and D0 inclusive $t\overline{t}$ forward–backward asymmetry is $A_{\mathrm{FB}}^{t\overline{t}}=(12.8\pm 2.1(\mathrm{stat}.)\pm 1.14(\mathrm{syst}.))\%=(12.8\pm 2.5)\%$. The precision of the combination is such that the $A_{\mathrm{FB}}$ is measured with a significance of 5 SD from zero asymmetry. The combined inclusive single-lepton asymmetry is $A_{\mathrm{FB}}^{\ell }=(7.3\pm 1.6(\mathrm{stat}.)\pm 1.12(\mathrm{syst}.))\%$, while the combined dileptonic asymmetry is $A_{\mathrm{FB}}^{\ell \ell }=(10.8\pm 4.3(\mathrm{stat}.)\pm 1.6(\mathrm{syst}.))\%$. All inclusive combined measurements together with the individual measurements used as the inputs to the combination and the theoretical predictions are summarized in Figure 24.

Differential measurements of $A_{\mathrm{FB}}^{t\overline{t}}$ as a function of $m_{t\overline{t}}$ were measured only in the $\ell +$jets channel and combined together, see Figure 25. For the combination, the data are fitted by a linear function. The obtained slope of $9.71\pm 3.28\times {10}^{-4}{\mathrm{Ge}\mathrm{V}}^{-1}$ is compatible with NNLO QCD + NLO EW prediction of ${5.11}_{-0.64}^{+0.42}\times {10}^{-4}{\mathrm{Ge}\mathrm{V}}^{-1}$ at the level of 1.3 SD. The differential $t\overline{t}$ asymmetry as a function of $\Delta y$ is available from CDF for both $\ell +$jets and dilepton channels, and from D0 for the $\ell +$jets channel, see Figure 25. Since the choice of the binning differs for these measurements, the simultaneous fit to a linear function with zero offset was performed for all available measurements employing the correlations. The slope parameter is measured to be $0.187\pm 0.038$ which is compatible with NNLO QCD + NLO EW prediction of ${0.129}_{-0.012}^{+0.006}$ at the level of 1.5 SD. The individual CDF and D0 measurements of $A_{\mathrm{FB}}^{\ell }$ as a function of $|q_{\ell }{\eta }_{\ell }|$ together with the individual measurements of $A_{\mathrm{FB}}^{\ell \ell }$ as a function of $|\Delta \eta |$ are shown in Figure 26 without any quantitative comparison to the prediction. Looking at the plots, there can not be seen any striking disagreement with NLO QCD + NLO EW prediction.

4.1.5. Summary and Discussion of Tevatron Measurements

All inclusive Tevatron measurements of forward–backward asymmetry at the parton level in the $t\overline{t}$ rest frame are summarized in

Table 7. Summary of Tevatron measurements of inclusive forward–backward asymmetries. For a given measurement, if there is just one uncertainty, it is combined statistical and systematic uncertainty. If there are two uncertainties, the first one is always statistical and the second one is systematic uncertainty.

Experiment, Channel	$\mathcal{L}$[${\mathbf{fb}}^{-1}$]	${\mathit{A}}_{\mathbf{FB}}^{\mathit{t}\overline{\mathit{t}}}$ [%]	${\mathit{A}}_{\mathbf{FB}}^{\mathbf{\ell }}$ [%]	${\mathit{A}}_{\mathbf{FB}}^{\mathbf{\ell }\mathbf{\ell }}$ [%]
CDF, $\ell +$jets	1.9	$24\pm 13\pm 4$
CDF, $\ell +$jets	5.3	$15.8\pm 7.4$
D0, $\ell +$jets	5.4	$19.6\pm 6.5$	$15.2\pm 4.0$
D0, dilepton	5.4		$5.8\pm 5.1\pm 1.3$	$5.3\pm 7.9\pm 2.9$
D0, combination	5.4		$11.8\pm 3.2$
CDF, $\ell +$jets	9.4	$16.4\pm 3.9\pm 2.6$	${10.5}_{-2.9}^{+3.2}$
CDF, dil	9.1	$12\pm 11\pm 7$	$7.2\pm 5.2\pm 3.0$	$7.6\pm 7.2\pm 3.9$
D0, $\ell +$jets	9.7	$10.6\pm 3.0$	${5.0}_{-3.7}^{+3.4}$
D0, dil	9.7	$17.5\pm 5.6\pm 3.1$	$4.4\pm 3.7\pm 1.1$	$12.3\pm 5.4\pm 1.5$
CDF, combination	9.7	$16.0\pm 4.5$	${9.0}_{-2.6}^{+2.8}$
D0, combination	9.7	$11.8\pm 2.5\pm 1.3$
Tevatron, combination	9.7	$12.8\pm 2.1\pm 1.4$	$7.3\pm 1.6\pm 1.2$	$10.8\pm 4.3\pm 1.6$

. These should be compared to the latest NNLO QCD + EW prediction of $A_{\mathrm{FB}}=(9.5\pm 0.7)\%$ [30] and the ${\mathrm{aN}}^3$LO QCD + EW prediction of $A_{\mathrm{FB}}=(10.0\pm 0.6)\%$ [29], while for the leptonic and dileptonic asymmetries only NLO QCD + EW predictions exist: $A_{\mathrm{FB}}^{\ell }=(3.8\pm 0.3)\%$ and $A_{\mathrm{FB}}^{\ell \ell }=(4.8\pm 0.4)\%$ [24].

The inclusive $A_{\mathrm{FB}}^{t\overline{t}}$ are all consistent between them for different channels and experiments, and are consistent with both NNLO QCD + EW and ${\mathrm{aN}}^3$LO QCD + EW predictions. The maximum deviation is 1.6 SD for D0 $\ell +$jets measurement using $5.4{\mathrm{fb}}^{-1}$ while the final Tevatron combination is 1.3 SD higher when compared to NNLO QCD + EW prediction. Similar conclusions hold also for the inclusive dileptonic asymmetry $A_{\mathrm{FB}}^{\ell \ell }$ with the maximum deviation at 1.3 SD in the D0 dileptonic measurement using $9.7{\mathrm{fb}}^{-1}$. However, it should be noted that all measurements are consistently higher than both NNLO QCD + EW and ${\mathrm{aN}}^3$LO QCD + EW predictions. For the inclusive leptonic asymmetry $A_{\mathrm{FB}}^{\ell }$ again all measurements are higher than the prediction. The biggest deviation is for the D0 measurement in the $\ell +$jets channel using $5.4{\mathrm{fb}}^{-1}$ at the level of 2.8 SD, while this has been lowered significantly with the full Run II statistics. The final Tevatron combination is only about 1.7 SD higher than prediction. It should be also noted that the prediction here is only at NLO QCD + EW level, so with the potential NNLO it is expected the deviation will be even lower. The dominant uncertainty in inclusive measurements is the statistical uncertainty.

The forward–backward asymmetry differential measurements at the Tevatron were performed as a function of $m_{t\overline{t}}$ and rapidity related observable $|\Delta y_{t\overline{t}}|$, $|y_{\ell }|$, and $\Delta {\eta }_{\ell \ell }$. The $m_{t\overline{t}}$ and $|\Delta y_{t\overline{t}}|$ dependencies are a bit stronger than expected but the agreement is within 2 SD.

4.2. LHC Measurements

Both ATLAS and CMS experiments started to perform the measurements of the charge asymmetry from the beginning of Run 1 at the energy $\sqrt{s}=7$ TeV. Initially, only the measurements in the $\ell +$jets channel and with a small luminosity of about $1{\mathrm{fb}}^{-1}$ were performed by ATLAS [65] and CMS [69].

Next measurements at $\sqrt{s}=7$ TeV were performed with the full statistics of 2011 year ($\approx 5{\mathrm{fb}}^{-1}$) in both $\ell +$jets and dilepton channels by both ATLAS [105,106] and CMS collaborations [107,108]. Afterwards, the measurements with about four times larger statistics (full 2012 year, $\approx 20{\mathrm{fb}}^{-1}$) at $\sqrt{s}=8$ TeV were again performed in both dilepton and $\ell +$jets channels and by both ATLAS [109,110,111] and CMS [112,113,114] collaborations.

In Run 2 at $\sqrt{s}=13$ TeV, CMS performed the measurement in both $\ell +$jets [115] and dilepton [116] channels using partial dataset (2015 + 2016 years, $\approx 36{\mathrm{fb}}^{-1}$). On the other hand, ATLAS performed the measurement in the $\ell +$jets channel with the full Run 2 statistics (years 2015–2018, $\approx 140{\mathrm{fb}}^{-1}$) [50]. However, it is for now only the preliminary measurement.

Moreover, ATLAS and CMS combined their measurements from Run 1 at $\sqrt{s}=7$ TeV and $\sqrt{s}=8$ TeV [91]. In the following, all these measurements will be briefly described.

4.2.1. Measurements at $\sqrt{s}=7$ TeV

The initial LHC measurement of $A_{\mathrm{C}}$ was performed by CMS using $1.09{\mathrm{fb}}^{-1}$ of luminosity [69]. The $A_{\mathrm{C}}^{t\overline{t}}$ was measured using distribution $\Delta \left|\eta \right|=|{\eta }_t|-|{\eta }_{\overline{t}}|$ and $\Delta y^2=(y_t-y_{\overline{t}})(y_t+y_{\overline{t}})$ shown in Figure 27. Using 12,757 data events with the expected background of $2520\pm 246$ events, the inclusive asymmetry is measured to be $A_{\mathrm{C}}^{t\overline{t},\eta }=(-1.7\pm 3.2{(\mathrm{stat}.)}_{-3.6}^{+2.5}(\mathrm{syst}.))\%$, and $A_{\mathrm{C}}^{t\overline{t},y}=(-1.3\pm 2.8{(\mathrm{stat}.)}_{-3.1}^{+2.9}(\mathrm{syst}.))\%$, consistent with the QCD NLO + EW predictions of $(1.36\pm 0.08)\%$ and $(1.15\pm 0.06)\%$ [21], respectively.

Similarly, the initial ATLAS measurement of the charge asymmetry was performed using $1.04{\mathrm{fb}}^{-1}$ of luminosity [65]. The measured inclusive asymmetry is $A_{\mathrm{C}}^{t\overline{t}}=(-1.9\pm 2.8(\mathrm{stat}.)\pm 2.4(\mathrm{syst}.))\%$ which is consistent with the NLO QCD + NLO EW prediction $A_{\mathrm{C}}=(1.23\pm 0.05)\%$ [24]. The differential measurement of the asymmetry as a function of $m_{t\overline{t}}$ was measured only in two bins and had large uncertainties.

The measurements at $\sqrt{s}=7$ TeV using full statistics were performed by both ATLAS and CMS in both $\ell +$jets and dilepton channels. In the $\ell +$jets channel, both ATLAS using $4.7{\mathrm{fb}}^{-1}$ [105] and CMS using $5.0{\mathrm{fb}}^{-1}$ [107] measure the asymmetry inclusively and and also differentially as a function of $m_{t\overline{t}}$, $y_{t\overline{t}}$, $p_{\mathrm{T},t\overline{t}}$. The inclusive results are $A_{\mathrm{C}}^{t\overline{t}}=(0.6\pm 1.0(\mathrm{stat}.+\mathrm{syst}.))\%$ for ATLAS and $A_{\mathrm{C}}^{t\overline{t}}=(0.4\pm 1.0(\mathrm{stat}.)\pm 1.1(\mathrm{syst}.))\%$ for CMS. The differential asymmetries are shown in Figure 28 and Figure 29.

In the dilepton channel, both ATLAS using $4.6{\mathrm{fb}}^{-1}$ [106] and CMS using $5.0{\mathrm{fb}}^{-1}$ [108] measure the $t\overline{t}$ and dileptonic asymmetry inclusively: $A_{\mathrm{C}}^{t\overline{t}}=(2.1\pm 2.5(\mathrm{stat}.)\pm 1.7(\mathrm{syst}.))\%$, $A_{\mathrm{C}}^{\ell \ell }=(2.4\pm 1.5(\mathrm{stat}.)\pm 0.9(\mathrm{syst}.))\%$ in ATLAS while $A_{\mathrm{C}}^{t\overline{t}}=(-1.0\pm 1.7(\mathrm{stat}.)\pm 0.8(\mathrm{syst}.))\%$, $A_{\mathrm{C}}^{\ell \ell }=0.9\pm 1.0(\mathrm{stat}.)\pm 0.6(\mathrm{syst}.))\%$ in CMS. The comparison of the inclusive ATLAS $A_{\mathrm{C}}^{t\overline{t}}$ and $A_{\mathrm{C}}^{\ell \ell }$ measurements to the theory prediction is shown in Figure 30. CMS also measured the dileptonic asymmetry as a function of $t\overline{t}$ mass, rapidity, and transverse momentum, see Figure 31.

To summarize the measurements at $\sqrt{s}=7$ TeV: both ATLAS and CMS measurements are in agreement with predictions. The most precise measurement of the $t\overline{t}$ charge asymmetry has a total uncertainty of 1.0%. The initial measurements with partial statistics had large (≈3%) and about the same statistical and systematic uncertainties. This is a bit different to the Tevatron measurements where statistical uncertainty was dominant in most of the measurements. This is mostly due to the large $t\overline{t}$ sample already available for initial measurements and the fact these were measurements at the very early of the LHC running, so the detectors were not well understood yet. The full statistics measurements improved both statistical and systematic precision considerably. They are now mostly limited by the statistical uncertainty, especially dilepton measurements. The differential measurements are also in agreement with the predictions, they are mostly statistically limited and not really even able to disfavor BSM models.

4.2.2. Measurements at $\sqrt{s}=8$ TeV

The measurements at $\sqrt{s}=8$ TeV with the full statistics were performed by both ATLAS and CMS in both $\ell +$jets and dilepton channels.

ATLAS performed two measurements in the $\ell +$jets channel using $20.3{\mathrm{fb}}^{-1}$ [109,110]. In the first analysis, the asymmetry is measured inclusively ($A_C=(0.9\pm 0.5(\mathrm{stat}.+\mathrm{syst}.))\%$) and also differentially as a function of $m_{t\overline{t}}$, $y_{t\overline{t}}$, $p_{\mathrm{T},t\overline{t}}$, and ${\beta }_{z,t\overline{t}}$, see Figure 32 using standard unfolding procedure [109]. The inclusive measurement is compatible with the NNLO QCD + NLO EW prediction $\left({0.97}_{-0.03}^{+0.02}\right)\%$. The second measurement focused on a large $t\overline{t}$ invariant mass region ($m_{t\overline{t}}>0.75$ TeV, another requirement is $|\Delta |y\left|\right|<2$) using reconstruction techniques specifically designed for the decay topology of highly boosted top quarks. In such cases, hadronicaly decaying top quarks are reconstructed as single large-radius jets with a specific jet substructure. In such phase space, the asymmetry is measured to be $A_{\mathrm{C}}^{t\overline{t}}=(4.2\pm 3.2(\mathrm{stat}.+\mathrm{syst}.))\%$. A differential measurement as a function of $m_{t\overline{t}}$is also performed, see Figure 33.

CMS also performed two measurements in the $\ell +$jets channel using $19.7{\mathrm{fb}}^{-1}$ [112] and $19.6{\mathrm{fb}}^{-1}$ [113], respectively. In the first measurement [112], the asymmetry is measured inclusively ($A_{\mathrm{C}}^{t\overline{t}}=(0.10\pm 0.68(\mathrm{stat}.)\pm 0.37(\mathrm{syst}.))\%$) and also differentially as a function of $m_{t\overline{t}}$, $y_{t\overline{t}}$, and $p_{\mathrm{T},t\overline{t}}$. Moreover, CMS performed here the first LHC measurement at the particle level in the fiducial phase space mimicking the selection criteria. The inclusive fiducial ($A_C^{t\overline{t},fid}=(-0.35\pm 0.72\pm 0.31)\%$) and differential measurements as a function of $m_{t\overline{t}}$, $y_{t\overline{t}}$, and $p_{\mathrm{T},t\overline{t}}$, see Figure 34, are consistent with NLO QCD + EW prediction (inclusive prediction is (1.01 ± 0.10)%).

The second CMS measurement in the $\ell +$jets channel used a template method [113]. In this method, templates based on the SM were created for symmetric and antisymmetric components of the measured distribution (${{\rm Y}}_{t\overline{t}}=tanh\Delta \left|y\right|$) for various $t\overline{t}$ production processes, see Figure 35. Fitting data to these templates, see Figure 36, the inclusive asymmetry was measured: $A_{\mathrm{C}}^{t\overline{t}}=(0.33\pm 0.26\pm 0.33)\%$ which was the most precise measurement of $A_{\mathrm{C}}$ at that time. However, the disadvantage of this measurement was that it was more model dependent on SM predictions compared to usual unfolding measurements.

In the dilepton channel using $20.3{\mathrm{fb}}^{-1}$, ATLAS measured the $t\overline{t}$ and dileptonic asymmetry at parton level in the full phase space and at the particle level in the fiducial phase space [111]. Both, the inclusive measurements at parton level ($A_{\mathrm{C}}^{t\overline{t}}=(2.1\pm 1.6(\mathrm{stat}.+\mathrm{syst}.))\%$, $A_{\mathrm{C}}^{\ell \ell }=(0.8\pm 0.6(\mathrm{stat}.+\mathrm{syst}.))\%$) and particle level ($A_{\mathrm{C}}^{t\overline{t}}=(1.7\pm 1.8(\mathrm{stat}.+\mathrm{syst}.))\%$, $A_{\mathrm{C}}^{\ell \ell }=(0.6\pm 0.5(\mathrm{stat}.+\mathrm{syst}.))\%$) are consistent with the predictions. The differential measurements in two bins were measured as a function of $m_{t\overline{t}}$, $p_{\mathrm{T},t\overline{t}}$, and ${\beta }_{z,t\overline{t}}$ for both $A_{\mathrm{C}}^{t\overline{t}}$ and $A_{\mathrm{C}}^{\ell \ell }$ in both full and fiducial phase spaces. The summary of dileptonic asymmetry measurements in the fiducial phase space is in Figure 37. The difference between the results at the parton and particle level is small given that the $t\overline{t}$ modeling systematics is not a dominant uncertainty.

CMS also measured the asymmetry in the dilepton channel using $19.5{\mathrm{fb}}^{-1}$ [114]. It measured the $t\overline{t}$ and dileptonic asymmetry inclusively ($A_{\mathrm{C}}^{t\overline{t}}=(1.1\pm 1.1(\mathrm{stat}.)\pm 0.7(\mathrm{syst}.))\%$, $A_{\mathrm{C}}^{\ell \ell }=(0.3\pm 0.6(\mathrm{stat}.)\pm 0.3(\mathrm{syst}.))\%$) and also differentially as a function of $m_{t\overline{t}}$, $y_{t\overline{t}}$, and $p_{\mathrm{T},t\overline{t}}$.

ATLAS and CMS combined their measurements performed at $\sqrt{s}=7$ TeV and $\sqrt{s}=8$ TeV [91]. Only measurements of the $t\overline{t}$ asymmetry in the $\ell +$jets channel are combined. The measurements in the dilepton channel were statistically limited and their inclusion would not improve the overall uncertainty. The combination of inclusive measurements at $\sqrt{s}=7$ TeV and $\sqrt{s}=8$ TeV yielded $A_{\mathrm{C}}^{t\overline{t}}=(0.5\pm 0.7(\mathrm{stat}.)\pm 0.6(\mathrm{syst}.))\%$ and $A_{\mathrm{C}}^{t\overline{t}}=(0.55\pm 0.23(\mathrm{stat}.)\pm 0.25(\mathrm{syst}.))\%$, respectively. The CMS template measurement at $\sqrt{s}=8$ TeV [113] was used in the combination for the inclusive measurement while CMS unfolding measurement at $\sqrt{s}=8$ TeV [112] was used for the combination of differential measurements as a function of $m_{t\overline{t}}$. The summary of the inclusive Tevatron forward–backward and LHC 8 TeV charge asymmetry measurements together with the predictions of various BSM models is shown in Figure 14. The combined ATLAS+CMS charge asymmetry as a function of the invariant mass of the $t\overline{t}$ system in comparison with theoretical predictions for the SM and two versions of a color-octet model is shown in Figure 38.

In summary, the measurements at $\sqrt{s}=8$ TeV provided a significant progress compared to $\sqrt{s}=7$ TeV measurements. The measurements still agree with the SM prediction. Both the statistical and systematic uncertainties decreased almost at the same rate. The most precise individual inclusive measurement had an uncertainty of about 0.42% while the combined 8 TeV measurement had a precision of 0.33%. For the first time, the statistical uncertainty was no longer dominating the uncertainty in all measurements. The systematic uncertainties were smaller or similar to the statistical ones in the CMS template measurement, most of the ATLAS dilepton measurements, the ATLAS high $m_{t\overline{t}}$ measurement, and the LHC combination at $\sqrt{s}=8$ TeV. The first fiducial level measurements at particle level were performed although their advantage was not yet much visible due to the fact that $t\overline{t}$ modeling systematics were still not dominant uncertainties. In addition, a specific measurement at high $m_{t\overline{t}}$ was performed.

4.2.3. Measurements at $\sqrt{s}=13$ TeV

CMS performed already two measurements at $\sqrt{s}=13$ TeV using a partial Run 2 dataset of $35.9{\mathrm{fb}}^{-1}$.

In the dilepton channel [116], the normalized distribution of ${\Delta \left|y\right|}_{t\overline{t}}$ is measured at parton and particle level while the distribution of ${\Delta \left|\eta \right|}_{\ell \ell }$ is measured at particle level, see Figure 39. Using these distributions, charge asymmetries are obtained: $A_{\mathrm{C}}^{t\overline{t}}\left(parton\right)=(1.0\pm 0.9(\mathrm{stat}.+\mathrm{syst}.))\%$, $A_{\mathrm{C}}^{t\overline{t}}\left(particle\right)=(0.8\pm 0.9(\mathrm{stat}.+\mathrm{syst}.))\%$, and $A_{\mathrm{C}}^{\ell \ell }\left(particle\right)=(-0.5\pm 0.4(\mathrm{stat}.+\mathrm{syst}.))\%$, which are compared to various SM predictions in Figure 40.

CMS also measured the forward–backward asymmetry in the $\ell +$jets channel at $\sqrt{s}=13$ TeV using $35.9{\mathrm{fb}}^{-1}$ [115]. This is a bit different measurement compared to all the other LHC measurements. The approximate forward–backward asymmetry $A_{\mathrm{FB}}^{\left(1\right)}$ is determined instead of edge–central charge asymmetry as measured in all the other LHC measurements. The template method is used based on $m_{t\overline{t}}$, $x_F=2p_L/\sqrt{s}$, and $\cos \theta *$ variables, where $p_L$ is the scaled longitudinal momentum $p_L$ of the $t\overline{t}$ system in the laboratory frame, and ${\theta }^{*}$ is the production angle of the top quark relative to the direction of the initial-state parton in the $t\overline{t}$ center-of-mass frame. The $q\overline{q}\to t\overline{t}$ differential cross-section in $\cos \theta$ can be expressed as a linear combination of symmetric and antisymmetric functions, where the antisymmetric function can be approximated as a linear function of $\cos \theta$ and parameter $A_{\mathrm{FB}}^{\left(1\right)}$. Such approximation describes the LO terms and interference terms expected from an s-channel resonance with chiral couplings. In such approximation, $A_{\mathrm{FB}}=A_{\mathrm{FB}}^{\left(1\right)}$. The generator level distributions for the above mentioned variables for the $t\overline{t}$ production initiated by different processes are shown in Figure 41. The application of fitting procedure yields $A_{\mathrm{FB}}^{\left(1\right)}=\left({4.8}_{-8.7}^{+9.5}{(\mathrm{stat}.)}_{-2.9}^{+2.0}(\mathrm{syst}.)\right)\%$. The result is consistent with the NLO QCD [13,21,118] and NNLO QCD prediction [32], although the statistical uncertainty is quite large.

ATLAS already performed a preliminary $A_{\mathrm{C}}$ measurement in the $\ell +$jets channel using the full Run 2 statistics ($139{\mathrm{fb}}^{-1}$) [50]. Altogether, more than four millions of $t\overline{t}$ candidates were selected in data events with the expected background of about $15\%$. The asymmetry is measured to be $A_{\mathrm{C}}=(0.60\pm 0.15(\mathrm{stat}.+\mathrm{syst}.))\%$, consistent with the NNLO QCD + NLO EW prediction of $\left({0.64}_{-0.06}^{+0.05}\right)\%$. Differential measurements in $m_{t\overline{t}}$ and ${\beta }_{z,t\overline{t}}$ were also performed, see Figure 42. Moreover, the charge asymmetry measurement was interpreted in the framework of an effective field theory (EFT). In EFT formalism the SM Lagrangian is extended with operators that encode the new physics phenomena. The Warsaw basis includes a complete set of dimension-six operators [119]. The charge asymmetry is affected by the difference $C^{-}=C^1-C^2$, where $C^1=C_u^1=C_d^1$ and $C^2=C_u^2=C_d^2$ are Wilson coefficients which are obtained from seven four-fermion operators in Warsaw basis by using a flavour-specific linear combination [120]. The constrains on $C^{-}$ are shown in Figure 43.

4.2.4. Summary of LHC Measurements

All inclusive charge asymmetry measurements performed at the LHC are summarized in

Table 8. Summary of inclusive $t\overline{t}$ and leptonic charge asymmetry measurements performed at the LHC. For a given measurement, if there is just one uncertainty, it is combined statistical and systematical uncertainty. If there are two uncertainties, the first one is statistical and the second one is systematic uncertainty. All measurements used $\Delta \left|y\right|$ variable except for the measurement with * which used $\Delta \left|\eta \right|$. All measurements were performed at the parton level except for the measurement with ** which was performed at particle level.

Experiment, Channel	$\sqrt{\mathit{s}}$ [TeV]	L [${\mathbf{fb}}^{-1}$]	${\mathit{A}}_{\mathbf{C}}^{\mathit{t}\overline{\mathit{t}}}$ [%]	${\mathit{A}}_{\mathbf{C}}^{\mathbf{\ell }\mathbf{\ell }}$ [%]
CMS, $\ell +$jets	7	1.1	$-1.7\pm {3.2}_{-3.6}^{+2.5}$ *
ATLAS, $\ell +$jets	7	1.1	$-1.9\pm 2.8\pm 2.4$
CMS, $\ell +$jets	7	5.0	$0.4\pm 1.0\pm 1.1$
CMS, dil	7	5.0	$-1.0\pm 1.7\pm 0.8$	$0.9\pm 1.0\pm 0.6$
ATLAS, $\ell +$jets	7	4.7	$0.6\pm 1.0$
ATLAS, dil	7	4.6	$2.1\pm 2.5\pm 1.7$	$2.4\pm 1.5\pm 0.9$
LHC, combination	7	5.0	$0.5\pm 0.7\pm 0.6$
CMS, $\ell +$jets	8	19.7	$0.10\pm 0.68\pm 0.37$
CMS, $\ell +$jets(template)	8	19.6	$0.33\pm 0.26\pm 0.33$
CMS, dil	8	19.5	$1.1\pm 1.1\pm 0.7$	$0.3\pm 0.6\pm 0.3$
ATLAS, $\ell +$jets	8	20.3	$0.9\pm 0.5$
ATLAS, dil	8	20.3	$2.1\pm 1.6$	$0.8\pm 0.6$
LHC, combination	8	20.3	$0.55\pm 0.23\pm 0.25$
CMS, dilepton	13	35.9	$1.0\pm 0.9$	$-0.5\pm 0.4$ **
ATLAS,$\ell +$jets	13	139	$0.60\pm 0.15$

. The $A_{\mathrm{C}}^{t\overline{t}}$ asymmetries should be compared with NLO QCD including electroweak corrections prediction [24] $(1.23\pm 0.05)\%$ at $\sqrt{s}=7$ TeV, NNLO QCD + NLO EW prediction [32] $\left({0.97}_{-0.03}^{+0.02}\right)\%$ at $\sqrt{s}=8$ TeV and $\left({0.64}_{-0.05}^{+0.06}\right)\%$ at $\sqrt{s}=13$ TeV. The $A_{\mathrm{C}}^{\ell \ell }$ asymmetries should be compared with NLO QCD + EW prediction $(0.70\pm 0.03)\%$ at $\sqrt{s}=7$ TeV [24], $(0.64\pm 0.03)\%$ at $\sqrt{s}=8$ TeV [24], and NLO QCD + EW prediction $(0.55\pm 0.03)\%$ at $\sqrt{s}=13$ TeV [25].

All LHC measurements at all energies are well within 2 SD consistent with the SM prediction. The measurements at $\sqrt{s}=7$ TeV are limited by the statistics with all of them at least to have the absolute uncertainty of 1%. The exception is the combination of ATLAS and D0 in the $\ell +$jets channel which has the total uncertainty of about 0.9%. At $\sqrt{s}=8$ TeV, there are already many measurements which have comparable statistical and total systematic uncertainty. The most precise is the combination of the ATLAS and CMS $\ell +$jets channel measurements which has the overall uncertainty of about 0.34% with the dominant systematic uncertainties due to calibration of jets and signal modeling. Finally at $\sqrt{s}=13$ TeV, the full statistics measurement are not yet available except for the preliminary ATLAS $\ell +$jets measurement. This measurement is already very precise at the absolute level of 0.15%, very well consistent with NNLO QCD + NLO EW prediction, and differs from zero by 4 standard deviations. This is the first evidence for non-zero charge asymmetry at the LHC. The early measurements are not precise enough to be able to observe the expected decrease of the asymmetry with the energy of interactions.

The leptonic asymmetries have for now uncertainties larger than 0.4% (particle level) and are all consistent with SM predictions.

The differential measurements are also consistent with the SM prediction. Most of the time, the statistical uncertainties are dominant, although in the latest ATLAS measurement at $\sqrt{s}=13$ TeV the total systematic uncertainties are comparable to statistical uncertainties except for high $m_{t\overline{t}}$ bins.

5. Discussion and Outlook

It is clear from the description in Section 3 and Section 4 that the long path and large effort in improving the theory and experiments has paid off. Although, some may be unhappy that tensions between theoretical calculations and experimental measurements mostly disappeared, the understanding of the $t\overline{t}$ charge asymmetry is much better now.

On the theoretical side, the progress has been enormous from only a partial NLO prediction for $A_{\mathrm{FB}}$ at the Tevatron which predicted negative asymmetry, through the full NLO prediction in the laboratory frame of about 5%, to the latest full NNLO QCD + NLO EW prediction for both $A_{\mathrm{FB}}$ at the Tevatron and $A_{\mathrm{C}}$ at the LHC and the aN${}^3$LO QCD + NLO EW prediction at the Tevatron. At the Tevatron, the predicted asymmetry is about 10% while it is around 1% at the LHC. Moreover, differential asymmetries have been also calculated at NNLO QCD + NLO EW too as a function of many variables such as $m_{t\overline{t}}$, $\Delta y$, $p_{\mathrm{T},t\overline{t}}$, ${\beta }_{z,t\overline{t}}$, and $\cos \theta$. The leptonic asymmetry has been calculated at NLO+EW order.

On the experimental side, there has been performed a full set of measurements for various observables. The very early measurements were performed just at the reco level. Later, this has been improved to perform measurements at the parton level and lately also at the particle level. There are now available not only inclusive measurements of both forward–backward and charge asymmetries, but also detailed differential measurements as a function of a few variables such as $m_{t\overline{t}}$, $p_{\mathrm{T},t\overline{t}}$, $\Delta y$, ${\beta }_{z,t\overline{t}}$. All inclusive $t\overline{t}$ asymmetry measurements of CDF, D0, ATLAS, CMS show a very good agreement with the NNLO QCD + NLO EW prediction with the largest disagreement of about 1.6 SD. The leptonic asymmetry measurements with the full Tevatron dataset and at the LHC also agree with the NLO QCD + EW prediction with the largest disagreement of about 2.3 SD for the CDF leptonic asymmetry measurement. However, it should be mentioned that all inclusive Tevatron measurements are higher than the NNLO QCD + NLO EW prediction, so it is possible that some non-negligible correction is still not calculated. At the LHC, the asymmetries both higher and lower compared to the best prediction have been measured. At the Tevatron, the non-zero forward–backward asymmetry ($\delta A_{\mathrm{FB}}/A_{\mathrm{FB}}=20\%$) has been observed now (with a significance of about 5 SD) and the leptonic asymmetry is measured with the relative precision of about 26%. For $A_{\mathrm{C}}$ at the LHC at $\sqrt{s}=13$ TeV, the evidence (significance of at least 3 SD) of non-zero charge asymmetry has been obtained and the relative precision is about 25%. Given that the dileptonic asymmetry has not been measured yet with the full LHC Run 2 statistics, the fact that dileptonic asymmetry is supposed to be smaller than $A_{\mathrm{C}}$, and the fact it can be measured only in the dilepton channel, its relative precision is for now only around $80\%$. Most of the inclusive measurements at both the Tevatron and the LHC have been statistically limited although the statistical and total systematic uncertainties are about the same in the LHC combination at $\sqrt{s}=7$ TeV and $\sqrt{s}=8$ TeV and in the latest measurement at $\sqrt{s}=13$ TeV. The $A_{\mathrm{FB}}$ and $A_{\mathrm{C}}$ asymmetries and their leptonic versions have been measured also differentially as a function of a few variables. Most of the measurements have been statistically limited, but this starts to change with the full LHC Run 2 statistics. The Tevatron results are very probably final, since the data taking finished already in 2011.

The LHC running will continue, mostly at the energy of $\sqrt{s}=14$ TeV and about 20 times more data ($3000{\mathrm{fb}}^{-1}$) are expected to be delivered by the end of the LHC lifetime. This will allow to improve the statistical uncertainty by at least a factor of 4–5 and the systematic uncertainties will become dominant. Based on the ATLAS measurement at $\sqrt{s}=13$ TeV, it can be expected the dominant systematic uncertainties will be the $t\overline{t}$ modeling, the jet energy calibration related uncertainties and the $W+$jets background modeling. These systematic uncertainties will become dominant also for differential measurements and this will allow to measure them in a more detail using more bins and the larger range. Eventually, the dileptonic asymmetry should be more precisely measured because the leptons are more precisely measured than top quarks and typically have smaller systematic related uncertainties. Moreover, it is expected that another LHC experiment, the LHCb, will be able to observe a non-zero $t\overline{t}$ charge asymmetry at the high-luminosity LHC [121]. Additionally, there is a possibility to measure different types of asymmetries, such as energy asymmetry between the top and antitop quarks [122].

At the potential Future Circular Collider (FCC) in $pp$ collisions at $\sqrt{s}=100$ TeV, the charge asymmetry is greatly diluted by the dominance of the $gg$ initial state. The SM expected value is $A_{\mathrm{C}}=0.12\%$ [123] which will make it very hard to measure. However, the asymmetry is enhanced in associated processes $t\overline{t}+Z$, $t\overline{t}+\gamma$ and mainly in $t\overline{t}+W$, where the asymmetry is enhanced by about a factor of ten due to the $t\overline{t}+W$ process being dominated by a $q\overline{q}$ initial state [123,124]. A relative statistical precision of about 3% is expected in the determination of $A_{\mathrm{C}}$ in the $t\overline{t}+W$ process [124].

At the linear $e^{+}{e}^{-}$ collider, the EW based forward–backward asymmetry in $e^{+}{e}^{-}\to t\overline{t}$ is expected [125,126]. The preliminary studies for the potential International Linear Collider at $\sqrt{s}=500$ GeV show that for the large asymmetry of about $40\%$ (depending on the polarization of the beams), the expected relative precision of about 2% can be achieved [125].

The asymmetry measurements should also help in the model independent search for a new BSM physics within the effective field theory approach by constraining the EFT coefficients related to the top quark production.

6. Conclusions

As the heaviest known elementary particle, the top quark and studies of its properties is a promising portal to the new physics beyond the Standard Model. The charge asymmetry in the $t\overline{t}$ production is the effect which is predicted to be present at higher orders in perturbative quantum chromodynamics and by necessity to be small, but it is highly enhanced in various theories beyond the Standard Model.

After unexpectedly large values of the forward–backward asymmetry in the top quark pair production were observed in initial measurements at the Tevatron, a lot of attention has been paid to it by the experimental and theoretical community. This allowed to perform precise and detailed tests of the SM at high energies. At present, the prediction is known at full next-to-next-to-leading order in perturbative QCD with complete next-to-leading order electroweak corrections. The full statistics Tevatron forward–backward and the LHC charge asymmetry results for the inclusive and differential measurements agree with the predictions very well, mostly within two standard deviations, with the largest deviation of about 2.3 standard deviation. The predicted forward–backward asymmetry at the Tevatron of about $10\%$ is now measured with a relative precision of 20%. At the LHC, although the effect is much smaller ($\approx 1\%$), the relative precision of the latest measurement is already at the level of about 25%.

In the coming years at the LHC and potential future colliders, it can be expected that more measurements will be performed at higher energies and in the processes like $t\overline{t}+W$ boson where the relative precision at the level of a few percent can be potentially achieved. Moreover, there is a possibility to measure a very large $t\overline{t}$ asymmetry in electroweak interactions at the lepton collider in polarized beams with a relative precision of a couple of percent. This will allow to precisely test the present theory at high energies and to potentially observe the presence of BSM effects or to constrain the BSM physics either by excluding particular models or by constraining parameters of effective theories.