Fluid-Structure Interaction of Wind Turbine Blade Using Four Different Materials: Numerical Investigation
Abstract
:1. Introduction
- In the published literature, there have been several studies that have investigated the effectiveness of the pitch angle on the HAWT output, either using just a few pitch angle values or using lower fidelity modeling. Consequently, a current understanding of how the pitch angle influences the turbine output is inadequate. The present study supplements the current information by using CFD calculations and FEA calculations that are validated against the standard empirical equations to investigate the impact of the blade pitch angle on the output parameter.
- The investigated operating conditions include five-pitch angles with increments of 4° and eight different wind speeds. No previous study has used these operating conditions to investigate the effects of pitch angles, which provides a more detailed understanding of how the wind turbine behavior changes for different pitch angles.
- In the previous literature, primarily the influence of pitch angles on the turbine output parameter has been studied. At the same time, the present research explains thoroughly how turbine blade pressures are altered in various pitch angles and wind speeds. Along with the change in pitch angle, this helps realistic assumptions to be made for the next step in the improvement of a horizontal axis wind turbine (HAWT) efficiency.
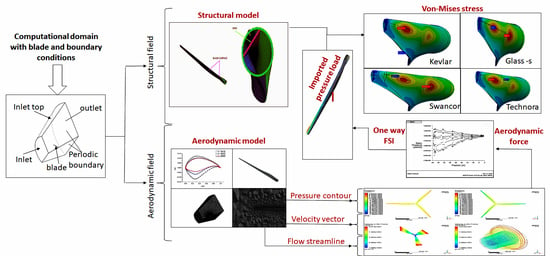
- The current study provides a comparison between the Von-Mises stress distribution of turbine blades for different pitch angles, different wind speeds, and different materials. To the best of our knowledge, this is the first study to report the pitch angle effect on Von-Mises stress distribution.
- Although the one-way fluid-structure interaction has been performed for the wind turbine, this technique has not been applied to study the effect of pitch angles on the performance parameter of the wind turbine blade by applying four different materials for structural analysis. A detailed analysis is conducted to clarify the influence of pitch angle on HAWT aerodynamics. The research examines the torque, power variance, pressure distribution, stress distribution, and deformation after changing various pitch angles, which the authors have previously not conducted in such detail for such turbines. The knowledge presented will significantly help researchers and design engineers to develop creative wind turbines that are more economical.
2. Methodology
2.1. CFD Modeling
2.1.1. Design of Wind Turbine Model
2.1.2. Computational Domain and Boundary Conditions
2.1.3. Meshing
2.1.4. Turbulence Modeling
2.1.5. Solution Setup
2.1.6. Residuals Convergence Criteria
2.2. FEA Modeling
2.3. One-way FSI Coupling
3. Results and Discussion
3.1. Three-Dimensional Simulations
3.1.1. Estimation of Torque and Power
3.1.2. Verifications
3.1.3. Pressure Distributions
3.1.4. Deformation and Von-Mises Stress
4. Conclusions
- A pitch angle of 16° is not suitable for the analysis and for the experimental purpose as it shows a decrease in the power value for wind speed.
- A pitch angle of 0°, 4°, and 8° has shown a better power outcome as compared to other pitches.
- The torque acting on the blade is maximum when a pitch angle of 4° and 8° is considered for the analysis.
- For every pitch angle and wind speed, a maximum deformation of the blade obtained for Kevlar, Technora, and Glass-s comes to be lower than the clearance of the tower (3.3 m), suggesting that, under all operating conditions, the blade cannot hit the tower.
- The maximum equivalent stress (Von-Mises stress) for Kevlar, Glass-S, and Glass-E are found to be well suited to the design limit.
- It is observed that for a pitch angle of 0°, velocity 11 m/s, pitch angle of 8°, velocity 20 m/s, pitch angle of 4°, velocity 24 m/s, and pitch angle of 10°, and velocity 10 m/s blade deformation exceeds the tower clearance when the Swancor-2511 A material is considered.
- The finding of the current study supports improvement of the aerodynamic performance of a horizontal axis wind turbine in the following ways:
- Optimization of the wind turbine blade is conceivable by detecting the best pitch angle.
- It is possible to boost the mean electrical power significance by outfitting wind turbines with section pitch angles distributions.
- Identifying best pitch angles can help in developing a control strategy to reduce loads fluctuation and regulate the power output.
- The results from the numerical simulation can help in developing a small wind turbine with various pitch angles, which can be tested inside a low-speed wind tunnel. This experiment can help in verifying the feasibility and efficiency of the turbine. The experimental results can be excellent benchmark data for the computational and theoretical modelers to validate their models before undertaking simulations of more realistic conditions both in terms of turbine support and geometry.
- This article can help the researcher derive an optimal blade pitch function based on the best pitch angle, which can further help in designing the blade pitch control device.
- From this study, one can identify the desirable pitch angle and can reduce the strength of the unsteady load caused by the wave current action without too much loss of power.
Author Contributions
Funding
Conflicts of Interest
References
- Global Wind Report 2018. Global Wind Energy Council. 11 October 2019. Available online: https://gwec.net/global-wind-report-2018/ (accessed on 25 March 2020).
- Dai, J.; Yang, X.; Wen, L. Development of wind power industry in China: A comprehensive assessment. Renew. Sustain. Energy Rev. 2018, 97, 156–164. [Google Scholar] [CrossRef]
- Premalatha, M.; Abbasi, T.; Abbasi, S.A. Wind energy: Increasing deployment, rising environmental concerns. Renew. Sustain. Energy Rev. 2014, 31, 270–288. [Google Scholar]
- Wang, L. Nonlinear Aeroelastic Modelling of Large Wind Turbine Composite Blades. Ph.D. Thesis, University of Central Lancashire, Preston, UK, 2015. [Google Scholar]
- Makridis, A.; Chick, J. Validation of a CFD model of wind turbine wakes with terrain effects. J. Wind Eng. Ind. Aerodyn. 2013, 123, 12–29. [Google Scholar] [CrossRef]
- Orlandi, A.; Collu, M.; Zanforlin, S.; Shires, A. 3D URANS analysis of a vertical axis wind turbine in skewed flows. J. Wind Eng. Ind. Aerodyn. 2015, 147, 77–84. [Google Scholar] [CrossRef] [Green Version]
- Plaza, B.; Bardera, R.; Visiedo, S. Comparison of BEM and CFD results for MEXICO rotor aerodynamics. J. Wind Eng. Ind. Aerodyn. 2015, 145, 115–122. [Google Scholar] [CrossRef]
- Tu, J.; Yeoh, G.H.; Liu, C. Computational Fluid Dynamics: A Practical Approach; Butterworth-Heinemann: Oxford, UK, 2018. [Google Scholar]
- Hansen, M.O.L.; Sørensen, J.N.; Voutsinas, S.; Sørensen, N.; Madsen, H.A. State of the art in wind turbine aerodynamics and aeroelasticity. Prog. Aerosp. Sci. 2006, 42, 285–330. [Google Scholar] [CrossRef]
- Zhang, P.; Huang, S. Review of aeroelasticity for wind turbine: Current status, research focus and future perspectives. Front. Energy 2011, 5, 419–434. [Google Scholar] [CrossRef]
- Wang, L.; Liu, X.; Renevier, N.; Stables, M.; Hall, G.M. Nonlinear aeroelastic modelling for wind turbine blades based on blade element momentum theory and geometrically exact beam theory. Energy 2014, 76, 487–501. [Google Scholar] [CrossRef]
- Wang, L.; Kolios, A.; Nishino, T.; Delafin, P.L.; Bird, T. Structural optimisation of vertical-axis wind turbine composite blades based on finite element analysis and genetic algorithm. Compos. Struct. 2016, 153, 123–138. [Google Scholar] [CrossRef] [Green Version]
- Sudhamshu, A.R.; Pandey, M.C.; Sunil, N.; Satish, N.S.; Mugundhan, V.; Velamati, R.K. Numerical study of effect of pitch angle on performance characteristics of a HAWT. Eng. Sci. Technol. Int. J. 2016, 19, 632–641. [Google Scholar]
- Rocha, P.C.; de Araujo, J.C.; Lima, R.P.; da Silva, M.V.; Albiero, D.; de Andrade, C.F.; Carneiro, F.O.M. The effects of blade pitch angle on the performance of small-scale wind turbine in urban environments. Energy 2018, 148, 169–178. [Google Scholar] [CrossRef]
- Rezaeiha, A.; Kalkman, I.; Blocken, B. Effect of pitch angle on power performance and aerodynamics of a vertical axis wind turbine. Appl. Energy 2017, 197, 132–150. [Google Scholar] [CrossRef] [Green Version]
- Ansari, M.; Nobari, M.R.H.; Amani, E. Determination of pitch angles and wind speeds ranges to improve wind turbine performance when using blade tip plates. Renew. Energy 2019, 140, 957–969. [Google Scholar] [CrossRef]
- Colombo, L.; Corradini, M.L.; Ippoliti, G.; Orlando, G. Pitch angle control of a wind turbine operating above the rated wind speed: A sliding mode control approach. ISA Trans. 2020, 96, 95–102. [Google Scholar] [CrossRef] [PubMed]
- Krueger, B.; Kratz, S.; Theopold, T.; Soter, S. Wear Reduction Control Method in a Blade Pitch System of Wind Turbines. In Proceedings of the 2019 IEEE 28th International Symposium on Industrial Electronics (ISIE), Vancouver, BC, Canada, 12–14 June 2019; pp. 1107–1112. [Google Scholar]
- Jiao, X.; Yang, Q.; Fan, B.; Chen, Q.; Sun, Y.; Wang, L. EWSE and Uncertainty and Disturbance Estimator Based Pitch Angle Control for Wind Turbine Systems Operating in Above-Rated Wind Speed Region. J. Dyn. Syst. Meas. Control 2020, 3, 142. [Google Scholar] [CrossRef]
- Yuan, Y.; Chen, X.; Tang, J. Multivariable robust blade pitch control design to reject periodic loads on wind turbines. Renew. Energy 2020, 146, 329–341. [Google Scholar] [CrossRef]
- Civelek, Z. Optimization of fuzzy logic (Takagi-Sugeno) blade pitch angle controller in wind turbines by genetic algorithm. Eng. Sci. Technol. Int. J. 2020, 23, 1–9. [Google Scholar] [CrossRef]
- Iqbal, A.; Ying, D.; Saleem, A.; Hayat, M.A.; Mehmood, K. Efficacious pitch angle control of variable-speed wind turbine using fuzzy based predictive controller. Energy Rep. 2020, 6, 423–427. [Google Scholar] [CrossRef]
- Kolios, A.; Chahardehi, A.; Brennan, F. Experimental determination of the overturning moment and net lateral force generated by a novel vertical axis wind turbine: Experiment design under load uncertainty. Exp. Tech. 2013, 37, 7–14. [Google Scholar] [CrossRef] [Green Version]
- Pintar, M.; Kolios, A.J. Design of a novel experimental facility for testing of tidal arrays. Energies 2013, 6, 4117–4133. [Google Scholar] [CrossRef]
- Fluent; ANSYS. Release 15.0. Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, November 2013. [Google Scholar]
- Mezaal, N.A.; Osintsev, K.V.; Alyukov, S.V. The computational fluid dynamics performance analysis of horizontal axis wind turbine. Int. J. Pow. Elec. Dri. Syst. ISSN 2019, 2088, 1073. [Google Scholar] [CrossRef]
- SolidWorks, D.S.; Street, W.; Waltham, M. SOLIDWORKS 2016. Available online: https://help.solidworks.com/2016/English/SolidWorks/sldworks/c_copyright_solidworks.htm?format=P&value= (accessed on 20 March 2015).
- Roul, R.; Kumar, A.; Mohanty, S.C. Numerical Investigation of Fluid Structure Interaction of 1.5 MW Wind Turbine Rotor Blade System. In Proceedings of the 2019 International Conference on Management Science and Industrial Engineering, Phuket, Thailand, 24–26 May 2019; pp. 254–259. [Google Scholar]
- Wang, L.; Quant, R.; Kolios, A. Fluid structure interaction modelling of horizontal-axis wind turbine blades based on CFD and FEA. J. Wind Eng. Ind. Aerodyn. 2016, 158, 11–25. [Google Scholar] [CrossRef] [Green Version]
- Bazilevs, Y.; Hsu, M.C.; Scott, M.A. Isogeometric fluid–structure interaction analysis with emphasis on non-matching discretizations, and with application to wind turbines. Comput. Methods Appl. Mech. Eng. 2012, 249, 28–41. [Google Scholar] [CrossRef]
- Hand, M.M.; Simms, D.A.; Fingersh, L.J.; Jager, D.W.; Cotrell, J.R.; Schreck, S.; Larwood, S.M. Unsteady Aerodynamics Experiment Phase VI: Wind Tunnel Test. Configurations and Available Data Campaigns (No. NREL/TP-500-29955); National Renewable Energy Laboratory: Golden, CO, USA, 2001.
- Wind Turbines Wake Turbulence and Separation. Arising Technology Systems Pty Limited ABN 32 079 817 342. Available online: https://www.arising.com.au/aviation/windturbines/wind-turbine.html (accessed on 25 March 2020).
- Menter, F. Zonal two equation kw turbulence models for aerodynamic flows. In Proceedings of the 23rd Fluid Dynamics, Plasmadynamics, and Lasers Conference, Orlando, FL, USA, 6–9 July 1993; p. 2906. [Google Scholar]
- Jones, W.P.; Launder, B.E. The prediction of laminarization with a two-equation model of turbulence. Int. J. Heat Mass Transf. 1972, 15, 301–314. [Google Scholar] [CrossRef]
- Wilcox, D.C. Formulation of the kw turbulence model revisited. AIAA J. 2008, 46, 2823–2838. [Google Scholar] [CrossRef] [Green Version]
- Sørensen, N.N.; Michelsen, J.A.; Schreck, S. Navier–Stokes predictions of the NREL phase VI rotor in the NASA Ames 80 ft × 120 ft wind tunnel. Wind Energy 2002, 5, 151–169. [Google Scholar] [CrossRef]
- Mo, J.O.; Lee, Y.H. CFD Investigation on the aerodynamic characteristics of a small-sized wind turbine of NREL PHASE VI operating with a stall-regulated method. J. Mech. Sci. Technol. 2012, 26, 81–92. [Google Scholar] [CrossRef]
- Anderson, J.D., Jr. Fundamentals of Aerodynamics; Tata McGraw-Hill Education: New York, NY, USA, 2010. [Google Scholar]
- Yelmule, M.M.; Vsj, E.A. CFD predictions of NREL phase VI rotor experiments in NASA/AMES wind tunnel. Int. J. Renew. Energy Res. 2013, 3, 261–269. [Google Scholar]
- Jureczko, M.E.Z.Y.K.; Pawlak, M.; Mężyk, A. Optimisation of wind turbine blades. J. Mater. Process. Technol. 2005, 167, 463–471. [Google Scholar] [CrossRef]
- Zhu, R.S.; Zhao, H.L.; Peng, J.Y.; Li, J.P.; Wang, S.Q.; Zhao, H. A numerical investigation of fluid-structure coupling of 3 MW wind turbine blades. Int. J. Green Energy 2016, 13, 241–247. [Google Scholar] [CrossRef]















| Parameters | Value | Unit |
|---|---|---|
| Rated power | 1500 | KW |
| No. of blades | 3.0 | Not Applicable |
| Rotor diameter | 86.5 | Metre |
| Rated wind speed | 11.5 | m/s |
| Rotational velocities | 21.21 | rpm |
| Pitch angle | 0, 4, 8, 12, 16, | degree |
| Velocities | 8, 9, 10, 11, 12, 16, 20, 24 | m/s |
| Factors | Values |
|---|---|
| Side boundaries | Periodic boundary condition |
| Pressure outlet | 1 atm |
| Turbulent intensity | 5% |
| Turbulent viscosity | 10 |
| Parameter | Mesh Size at the Blade Surface | |||
|---|---|---|---|---|
| 0.5 m | 0.4 m | 0.3 m | 0.2 m | |
| Torque (Nm) | 12,895 | 18,365 | 22,518 | 23,097 |
| elements | 163,217 | 208,431 | 356,628 | 624,099 |
| Control Method | Type of Mesh | Sizing | |||
|---|---|---|---|---|---|
| Global mesh control | Tetrahedral | Advance size function | |||
| Curvature (coarse) | Proximity (medium) | ||||
| nodes | elements | nodes | Elements | ||
| 32,736 | 185,999 | 60,778 | 34,3017 | ||
| Local mesh control | hexahedral | Steps | nodes | element | |
| Match control | 71,643 | 356,628 | |||
| Element size | 0.3 | ||||
| Inflation | |||||
| Sphere of influence | |||||
| Sphere radius | 30 m | ||||
| Element size | 2 m | ||||
| Material Name | Elastic Modulus [GPa] | Density [Kg/m3] |
|---|---|---|
| Kevlar | 179 | 1470 |
| Technora | 70 | 1390 |
| Glass-S | 88 | 2540 |
| Swancor-2511A | 19.2 | 1859 |
| Pitch (Degree) | V (m/s) | Tangential Velocity | ||
|---|---|---|---|---|
| Numerical | Analytical | Error (%) | ||
| 8° | 12 | 98 | 96.015 | 2.067 |
| Material | Radial Force (N) | Material | Radial Force (N) | ||||
|---|---|---|---|---|---|---|---|
| Kevlar | Technora | ||||||
| Pitch (Degree) | V (m/s) | Numerical | Analytical | Error (%) | Numerical | Analytical | Error (%) |
| 8° | 12 | 1.50 × 106 | 1,473,265.61 | 1.92323677 | 1.42 × 106 | 1,418,564 | 0.101206 |
| Material | Radial Force (N) | Material | Radial Force (N) | ||||
|---|---|---|---|---|---|---|---|
| Swancor-2511 A | Glass-S | ||||||
| Pitch (Degree) | V (m/s) | Numerical | Analytical | Error (%) | Numerical | Analytical | Error (%) |
| 8° | 12 | 1.89 × 106 | 1,888,030.386 | 0.088431517 | 2.59 × 106 | 2,592,159.361 | 0.059435 |
| Velocity (m/s) | Glass-S (m) | Kevlar (m) | Technora (m) | Swancor-2511 A (m) |
|---|---|---|---|---|
| 8 | 0.55123 | 0.29617 | 0.70182 | 1.7665 |
| 9 | 0.61139 | 0.33111 | 0.78548 | 1.9949 |
| 10 | 0.67586 | 0.36432 | 0.86468 | 2.1908 |
| 11 | 0.73686 | 0.39832 | 0.94582 | 3.3891 |
| 12 | 0.79715 | 0.43714 | 1.0252 | 2.5813 |
| 16 | 1.1564 | 0.56919 | 1.4525 | 5.1838 |
| 20 | 0.050511 | 0.016281 | 0.036135 | 0.12669 |
| 24 | 1.2694 | 0.69886 | 1.6568 | 4.1439 |
| Velocity (m/s) | Glass-S (m) | Kevlar (m) | Technora (m) | Swancor-2511 A (m) |
|---|---|---|---|---|
| 8 | 0.22622 | 0.11255 | 0.26859 | 0.70576 |
| 9 | 0.26927 | 0.14384 | 0.34039 | 0.8738 |
| 10 | 0.3363 | 0.17497 | 0.41434 | 1.0701 |
| 11 | 0.39292 | 0.20617 | 0.48803 | 1.2587 |
| 12 | 0.45096 | 0.23819 | 0.56308 | 1.4486 |
| 16 | 0.67612 | 0.3682 | 0.87393 | 2.2185 |
| 20 | 0.90612 | 0.49018 | 1.1666 | 2.9492 |
| 24 | 1.0938 | 0.5971 | 1.4175 | 3.5604 |
| Velocity (m/s) | Glass-S (m) | Kevlar (m) | Technora (m) | Swancor-2511 A (m) |
|---|---|---|---|---|
| 8 | 0.13246 | 0.060564 | 0.14079 | 0.39237 |
| 9 | 0.18135 | 1.19 ×107 | 0.21102 | 0.56543 |
| 10 | 0.23053 | 0.11691 | 0.27955 | 0.73666 |
| 11 | 0.27816 | 0.14886 | 0.3526 | 0.90654 |
| 12 | 0.3461 | 0.17977 | 0.42606 | 1.1046 |
| 16 | 0.57654 | 0.30864 | 0.73251 | 1.876 |
| 20 | 1.6784 | 0.92248 | 2.1815 | 5.4573 |
| 24 | 1.008 | 0.54747 | 1.301 | 3.2951 |
| Velocity (m/s) | Glass-S (m) | Kevlar (m) | Technora (m) | Swancor-2511 A (m) |
|---|---|---|---|---|
| 8 | 0.05974 | 0.061052 | 0.13894 | 0.23501 |
| 9 | 0.26174 | 0.16522 | 0.39661 | 0.9515 |
| 10 | 0.22748 | 0.14308 | 0.3439 | 0.83118 |
| 11 | 0.52217 | 0.11596 | 0.2827 | 0.6858 |
| 12 | 0.14146 | 0.090755 | 0.21136 | 0.52744 |
| 16 | 0.061012 | 0.032496 | 0.047455 | 0.15458 |
| 20 | 0.27501 | 0.14175 | 0.34118 | 0.89583 |
| 24 | 0.51484 | 0.27271 | 0.64256 | 1.6647 |
| Velocity (m/s) | Glass-S (m) | Kevlar (m) | Technora (m) | Swancor-2511 A (m) |
|---|---|---|---|---|
| 8 | 0.49259 | 0.28613 | 0.68602 | 1.7075 |
| 9 | 1.4003 | 0.27395 | 0.65709 | 1.636 |
| 10 | 0.89309 | 0.4395 | 1.1227 | 4.0426 |
| 11 | 0.043996 | 0.21269 | 0.53191 | 1.7097 |
| 12 | 0.45884 | 0.23969 | 0.61567 | 2.1882 |
| 16 | 0.22886 | 0.1448 | 0.34868 | 0.84425 |
| 20 | 0.039418 | 0.034896 | 0.086884 | 0.19509 |
| 24 | 0.21318 | 0.0905 | 0.22869 | 0.89097 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roul, R.; Kumar, A. Fluid-Structure Interaction of Wind Turbine Blade Using Four Different Materials: Numerical Investigation. Symmetry 2020, 12, 1467. https://doi.org/10.3390/sym12091467
Roul R, Kumar A. Fluid-Structure Interaction of Wind Turbine Blade Using Four Different Materials: Numerical Investigation. Symmetry. 2020; 12(9):1467. https://doi.org/10.3390/sym12091467
Chicago/Turabian StyleRoul, Rajendra, and Awadhesh Kumar. 2020. "Fluid-Structure Interaction of Wind Turbine Blade Using Four Different Materials: Numerical Investigation" Symmetry 12, no. 9: 1467. https://doi.org/10.3390/sym12091467
APA StyleRoul, R., & Kumar, A. (2020). Fluid-Structure Interaction of Wind Turbine Blade Using Four Different Materials: Numerical Investigation. Symmetry, 12(9), 1467. https://doi.org/10.3390/sym12091467