1. Introduction
The central concept for describing the structure of crystalline solids is that of the unit cell, the periodic repetition of which results in a spatially extended crystal exhibiting particular symmetries. For both three- and two-dimensional (3D and 2D) crystals, the enumeration of possible unit cell symmetries was first carried out by E.S. Fedorov at the end of the nineteenth century [
1,
2,
3]. Deriving the possible (3D or 2D) unit cell symmetries requires combining a crystal’s possible point group symmetry operations (rotations, rotation-inversions or reflections leaving one point of the crystal lattice invariant) with translations. It is well known that for three dimensions, this results in 230 so-called “space groups”. For two dimensions, only 17 planar groups, the so-called “wallpaper groups”, are possible. All information on space/wallpaper groups is nowadays collected in the many-volume
International Tables for Crystallography [
4,
5,
6,
7,
8].
The information compiled in the “
International Tables” [
4,
5,
6,
7,
8] is particularly useful for interpreting diffraction experiments: X-ray, neutron, and electron diffraction are the de facto methods for crystal structure determination and provide access not only to a crystal’s space group but also to the contents of its unit cell. In particular, the notion of extinctions (systematic absences of certain types of reflections due to specific symmetries present in the structure) is often fundamental for correctly determining a crystal’s space group.
The crystallinity—in other words, translational periodicity—of a solid is the essential starting-point in solid-state physics. For example, the quantum theory of electrical conductivity, involving Bloch waves, completely relies on the repetition of a unit cell for the concepts of reciprocal space and band structures to be valid (see e.g., [
9]). Surprisingly, while the translational periodicity of a solid is used extensively in theory, considerations concerning the unit cell’s symmetry are far less frequently encountered.
Translational symmetry naturally leads to a Fourier series. Submitting a Fourier series to additional symmetry constraints then results in relations between Fourier coefficients, or even in the vanishing of certain terms of the Fourier series. In this paper, we revisit the symmetry-adapted Fourier series for the planar wallpaper groups, and focus on the symmetry pattern formed by equivalent Fourier coefficients in 2D discrete coefficient space. Apart from the explicit expressions for the symmetry-adapted Fourier series and the symmetry relations between Fourier coefficients, we provide visualisations showing how direct-space symmetry is transformed into coefficient-space symmetry.
In the first sections of the paper (
Section 2,
Section 3 and
Section 4) we provide a pedestrian approach to the problem, work out some examples in detail, and make the link with the information contained in the “
International Tables” [
4,
5,
6,
7,
8] used by crystallographers. The bulk of the paper is formed by the 17 tables with detailed information on the Fourier series and Fourier coefficients for each of the wallpaper groups (
Section 5). In
Section 6, we discuss some points in more detail and summarise our results.
While the paper is hoped to have pedagogical merits, we also strive for completeness and applicability: The information derived is relevant for present-day materials science. For example, graphene [
10], a 2D honeycomb network of carbon atoms, is at present one of the most extensively investigated materials. Its equilibrium properties (e.g., electronic density) are expected to display the 2D symmetry of its underlying atomic structure (wallpaper group
, see below).
5. Wallpaper Group Tables
In the preceding sections we have shown how wallpaper group symmetry can be used to construct maximally-symmetric 2D Fourier series. The derivations and examples given contain many of the mathematical issues involved. At this point, it should be clear how to proceed for obtaining symmetry properties of Fourier coefficients and the Fourier series itself for a given wallpaper group.
We have made a systematical investigation of all wallpaper groups; in
Table 4,
Table 5,
Table 6,
Table 7,
Table 8,
Table 9,
Table 10,
Table 11,
Table 12,
Table 13,
Table 14,
Table 15,
Table 16,
Table 17,
Table 18,
Table 19,
Table 20,
Table 21 and
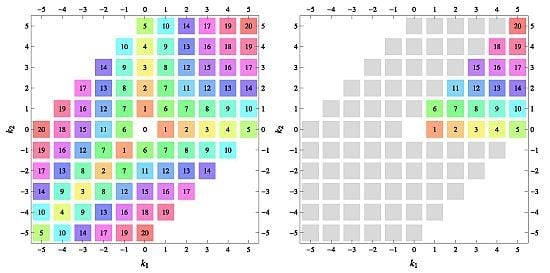
Table 22 all relevant wallpaper group information (Fourier coefficients symmetry property, independent Fourier coefficients domains, Fourier series) is summarized visually and analytically. The upper part of each table contains the wallpaper group’s label, the Bravais lattice type, the direct and the reciprocal basis vectors. Then, an example (a contour plot spanning four unit cells of a real function
) displaying translational and point group symmetry is shown; the values of the non-vanishing Fourier coefficients used for the example are indicated below the contour plot. Basis vectors and a possible choice for the asymmetric unit are drawn on the figure. Next to the example, the domains showing equivalence of Fourier coefficients are shown. The total domain
D shows which coefficients in the range
are equivalent (equal or opposite);
coordinates with equivalent Fourier coefficients
are given a same color and number. When not all equivalent
coordinates of a point lie in the range
, that point is left blank and unnumbered. (This occurs only for the hexagonal wallpaper groups.) To the right of the total domain
D, the subdomain
containing exactly one independent representative (colored and numbered) of each set of equivalent points is shown; the remaining points are now shown shaded gray and unnumbered. For
, an infinite number of possible choices exists; we recall that for a given cycle
of Fourier coefficient indices
generated by the symmetry property for Fourier coefficients, only one pair of indices
should be contained within
. For, e.g.,
(
Table 5), one could equally well take
,
rather than
,
. Our choices for
are simply based on convenience. In the case of subdomains with different cycles, the decomposition is shown below
D and
. The origin
is always excluded from the subdomain
(but included in the total domain
D), which is why the notation
is used for subdomains with cycle 1 excluding
. Opposite Fourier coefficients are shown by discs and squares of the same color and labeled with a same number in the total domain
D. In the case of necessarily vanishing Fourier coefficients, the symbol “⌼” is used. Below the example and the domains, the symmetry property for Fourier coefficients is given. To the right, if applicable, implications of the symmetry rule on the vanishing of Fourier coefficients (“extinction rules”) are given. Next, an explicit, symmetry-adapted, expression for the Fourier series of
is given, containing only (apart from the
term) independent coefficients from the subdomain
. Finally, an elaborated version of the reality criterion is given: The complex conjugate of
with
is equated to an expression involving the same or another coefficient in
. Implications on the reality of coefficients are given to the right, if applicable.
For the centered rectangular wallpaper groups
and
, alternate (non-primitive) versions of the tables are given as well, with Fourier indices labeled
and
(
Table 9 and
Table 14).
It is interesting to see how for each group, the real-space (point-group) symmetry is converted into coefficient-space symmetry. Indeed, the distribution of equivalent Fourier coefficients in domain D also displays rotation axes and mirror axes. Particularly intriguing is how the hexagonal groups divide coefficient space into 3-, 6- or 12-cycle domains.
6. Discussion and Conclusions
Having established
Table 4,
Table 5,
Table 6,
Table 7,
Table 8,
Table 9,
Table 10,
Table 11,
Table 12,
Table 13,
Table 14,
Table 15,
Table 16,
Table 17,
Table 18,
Table 19,
Table 20,
Table 21 and
Table 22, it is useful to consider some points in more detail.
A first issue is the reality criterion. Trivially, for all wallpaper groups, for
to be real,
must be real. Considering general coefficients
, it follows from Equation (
8) and the
symmetry property (
Table 5) that for wallpaper groups having a 2-fold rotation axis at the origin, all coefficients
must be real for
to be real. Since in two dimensions a 2-fold rotation axis is equivalent to an inversion center, we can speak of centrosymmetric and non-centrosymmetric wallpaper groups. The reality criteria for the non-centrosymmetric groups are summarized in
Table 23. As indicated already when discussing examples in the preceding sections, for a non-centrosymmetric wallpaper group, the reality criterion imposes further restrictions on the coefficients in the subdomain
. In general, a coefficient in
needs to be equal to the complex conjugate of another coefficient in
; in some special cases, this results in the reality of Fourier coefficients (see
Table 23). It is important to note, however, that the definition in terms of matrices of the inversion operation used throughout the “International Tables” [
4,
5,
6,
7,
8] is not only that the inversion matrix is the negative of the identity matrix but also that its determinant is negative. In that sense, there can be no inversion in two dimensions, and centrosymmetric and non-centrosymmetric wallpaper groups should rather be referred to as displaying and lacking 2-fold rotational symmetry, respectively.
A second point is the necessary vanishing of certain Fourier coefficients. As demonstrated in
Section 2, a glide reflection axis introduces a phase factor in the symmetry property for the Fourier coefficients, which in turn leads to certain Fourier coefficients having to be zero. This occurs for the groups
,
,
and
(all containing a “
g” in their label). Observed rules for vanishing coefficients are
or
, with
. These are analogous to the diffraction extinction rules associated with the presence of glide reflection axes [
4,
5,
6,
7,
8]. The centering operation discussed in
SubSection 4.5 also implies Fourier coefficients to be zero (
,
)—in analogy with the diffraction extinction rules for centered unit cells [
4,
5,
6,
7,
8].
A next issue is that of the notion of a “minimal” Fourier series. To correctly represent a given wallpaper group symmetry, a Fourier series must indeed contain sufficient non-vanishing Fourier coefficients resulting in the correct
x- and
y-dependence. Let us for example consider the group
(
Table 12). Trivially, if we take only the term
we have no
-dependence. If we take only
or
different from zero (
symmetry implies
) we create a function with only
x- or
y-dependence, respectively. This is illustrated in
Figure 9(a,b). If we assign, however, simultaneously both to
and
non-zero values, we have a
-dependent function, but its periodicity in both
x- and
y-direction is half that of the intended lattice, and the symmetry of the reduced unit cell is
[
Figure 9(c)]. The series with only
“switched on” results in a function with the right translational symmetry, and does indeed have
symmetry, but its asymmetric unit has half the size of the general
asymmetric unit [
Figure 9(d)]: The wallpaper group is actually
(compare
Table 12 and
Table 14). While independence on
x and/or
y and periodicity reduction can be relatively easily avoided by inspecting the explicit expression of the Fourier expansion and including necessary (low-
and low-
) Fourier coefficients, the last observation (a
Fourier series displaying
symmetry) involves more subtle considerations. It can be understood by realising that the
group is a subgroup of the
group. A rectangular lattice Fourier series with
(and all other Fourier coefficients equal to zero) fulfills both the symmetry properties of
and
, which can be clearly seen by comparing the domains
D of
Table 12 and
Table 14. Even more, it also complies with the symmetry of the
wallpaper group (
Table 10), which is also a subgroup of
(see also
SubSection 4.5). The net symmetry will therefore be that of the higher-symmetry group,
. To have a Fourier series with true
(or
) symmetry, it is necessary to include non-zero coefficients
with
odd, as in the example in
Table 12 where both
and
have been assigned non-zero values. Hence, to avoid apparent higher symmetry, a wallpaper group should be compared with any supergroup of which it is a subgroup; its pattern of non-zero and equivalent Fourier coefficients should distinguish itself from that of the supergroup. As a further illustration, let us consider the wallpaper groups
and
(
Table 21 and
Table 22, respectively). The former is a subgroup of the latter. If the expression for the Fourier expansion for a
function contains only Fourier coefficients that belong to the
subdomain of the
group, this will result in a function displaying
symmetry. A true
function therefore needs to contain at least one non-zero Fourier coefficient from the
-
subdomain. The example functions in the preceding sections and in
Table 4,
Table 5,
Table 6,
Table 7,
Table 8,
Table 9,
Table 10,
Table 11,
Table 12,
Table 13,
Table 14,
Table 15,
Table 16,
Table 17,
Table 18,
Table 19,
Table 20,
Table 21 and
Table 22 have been selected carefully to yield true wallpaper group symmetry with a small number of non-vanishing Fourier coefficients (in every example, only two independent coefficients were assigned non-zero values).
A more formal approach for deriving minimal symmetry-adapted functions for the wallpaper groups involves group theory; each wallpaper group should be decomposed into irreducible representations (IRREPs) [
12]. The terms of the Fourier series developed in this work should then be rearranged into linear combinations
that belong to the different IRREPs of the wallpaper group. The linear combinations belonging to the unit representation then display the full wallpaper group symmetry without apparent higher symmetry [
13]. The situation is similar to the decomposition of (planar) point groups. For example, the lowest-order function displaying
point group symmetry is
or, in polar coordinates,
. A decomposition of the wallpaper groups into IRREPs is beyond the scope of the present paper.
Finally, a few suggestions on how to use the Fourier series developed in this work. Our motivation came from the need of a continuous and infinitely differentiable function with the symmetry of the graphene lattice—
i.e., the
wallpaper group. In the context of solid-state physics, the 2D functions
with wallpaper group symmetry that naturally come to mind are (complex) electronic wave functions
or (real) electronic densities
of the new family of 2D materials like graphene or boron-nitride. Electronic densities can nowadays be calculated from ab-initio principles; a first application of our calculations could therefore be the fit of an ab-intio obtained electronic density to the symmetry-adapted Fourier series. By limiting the number of fitted coefficients [calculated numerically via Equation (
6)], one obtains a handy, analytical expression for
, which can then subsequently be used in further calculations. If necessary, the extension of the density above and below the atomic plane can be taken into account by making the Fourier coefficients
z-dependent.
Another situation where symmetry-adapted Fourier series could be used is when fitting X-ray diffraction data to a structural model. Rather than putting atoms in the unit cell and adjusting their positions and the unit cell’s parameters, one could conceive an approach where a limited number of Fourier coefficients of the electronic density —responsible for the scattering of X-rays—is taken as the adjustable parameter set (together with the unit cell’s dimensions), after which an atomic distribution matching the electronic density can be sought.
Note that the results obtained here can also be used for identifying or discriminating wallpaper groups (see e.g., [
14]): A numerical calculation of the Fourier coefficients of a given function
and testing for Fourier coefficient symmetry properties can indeed help to distinguish the planar symmetry of
.
Planar wallpaper groups are not only relevant for describing 2D crystals but also useful for analysing surfaces of three-dimensionally periodic crystals, and they can be a tool for studying crystal growth [
15].
In summary, it is hoped that the symmetry-adapted Fourier series presented in this paper will turn out to be useful for dealing with periodic functions in two dimensions in various situations.