The Graph, Geometry and Symmetries of the Genetic Code with Hamming Metric

Lenstra, Reijer

doi:10.3390/sym7031211

Open AccessArticle

The Graph, Geometry and Symmetries of the Genetic Code with Hamming Metric

by

Reijer Lenstra

Route Cantonale 103, Saint Sulpice VD 1025, Switzerland

Symmetry 2015, 7(3), 1211-1260; https://doi.org/10.3390/sym7031211

Submission received: 28 April 2015 / Revised: 20 June 2015 / Accepted: 7 July 2015 / Published: 14 July 2015

(This article belongs to the Special Issue Symmetry and Asymmetry in Biology)

Download

Browse Figures

Versions Notes

Abstract

:

The similarity patterns of the genetic code result from similar codons encoding similar messages. We develop a new mathematical model to analyze these patterns. The physicochemical characteristics of amino acids objectively quantify their differences and similarities; the Hamming metric does the same for the 64 codons of the codon set. (Hamming distances equal the number of different codon positions: AAA and AAC are at 1-distance; codons are maximally at 3-distance.) The CodonPolytope, a 9-dimensional geometric object, is spanned by 64 vertices that represent the codons and the Euclidian distances between these vertices correspond one-to-one with intercodon Hamming distances. The CodonGraph represents the vertices and edges of the polytope; each edge equals a Hamming 1-distance. The mirror reflection symmetry group of the polytope is isomorphic to the largest permutation symmetry group of the codon set that preserves Hamming distances. These groups contain 82,944 symmetries. Many polytope symmetries coincide with the degeneracy and similarity patterns of the genetic code. These code symmetries are strongly related with the face structure of the polytope with smaller faces displaying stronger code symmetries. Splitting the polytope stepwise into smaller faces models an early evolution of the code that generates this hierarchy of code symmetries. The canonical code represents a class of 41,472 codes with equivalent symmetries; a single class among an astronomical number of symmetry classes comprising all possible codes.

Keywords:

code evolution; Euclidian space; Hamming distance; Polya coloring; polytope; similarity pattern; mirror reflection group; permutation group; tetrahedron; quaternary code

Graphical Abstract

1. Introduction

The canonical genetic code as summarized by the codon table (Figure 1) consists of 64 codons or code words and each word encodes a single message—an amino acid or stop codon. The code is a mapping of the set of 64 codons onto 21 messages. All extant living organisms use this code, or minor variations thereof to synthesize the proteins encoded by their genomes [1,2]. This fact strongly argues in favor of the commonly held hypothesis that all known life evolved from a Last Universal Common Ancestor (LUCA), and that the code itself evolved in an RNA world inhabited by pre-LUCA organisms over 3.5 Billion years ago [3,4]. The code displays patterns of similarities [5,6]. Most messages are encoded by several synonymous codons (the degeneracy of the code), but the coloring of the codon table in Figure 1 shows broader patterns of similarities as well. The color scheme shows the Polar Requirement of the amino acids (Figure 2), a physicochemical characteristic frequently used for the analysis of the genetic code [7]. In the codon table, amino acids with similar Polar Requirements tend to cluster together; that is, they tend to be encoded by similar codons. Simplified amino acid alphabets consist of various sets of similar amino acids, such as a size-2 alphabet composed of a set of hydrophobic and a set of hydrophilic amino acids, and as will be discussed in Section 6, amino acids belonging to the same set are often grouped together in the codon table. Simplified amino acid alphabets based on physicochemical properties are not essentially different from those using protein sequence or structure information [8]. Codons are three letter words made up from a four letter alphabet {A, C, G, U}, and codons encoding the same message most often differ in the third codon position only, while codons encoding similar amino acids usually differ only in one or two positions. The Hamming metric of mathematical coding theory measures these differences between code words: words differing at one, two or three positions are at Hamming 1-, 2-, or 3-distance, respectively [9]. 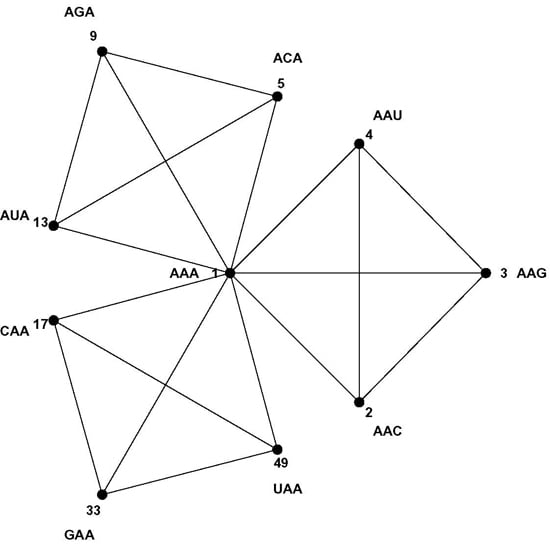The codon set combined with the Hamming metric makes a normed metric space of 64 points with well-defined distances between them. For example, each codon has nine nearest neighbor codons at 1-distance—nine codons differing at only one position, the most similar codons in the codon set by the Hamming metric; such as the nine nearest neighbors of codon AAA: AAC, AAG, AAU, ACA, AGA, AUA, CAA, GAA and UAA. The similarity patterns of the code result from the mapping of the codon space onto the message space and their mathematical analysis is the subject of this paper. As a first step we develop a geometric model of the code that faithfully maps Hamming distances onto Euclidian distances—the CodonPolytope (Section 4). In this model the codons are represented by 64 points in Euclidian 9-space, the vertices of a 9-dimensional geometric object (containing lower dimensional objects such as cubes and tetrahedrons). While the codon set with Hamming metric possesses permutation symmetries that preserve this metric, the polytope displays Euclidian symmetries and space coordinates that greatly facilitate the (computational) analysis of the similarity patterns of the code (Section 5, Section 6 and Section 7).

In 1950 Hamming published his now famous geometric cube model for binary codes: the code words are represented by vertices, and vertices representing code words differing at only one position are connected by edges [10,11]. The 3-bit binary code neatly illustrates this idea: the code word 000 is represented by a vertex with space coordinates (0,0,0) at the origin of a 3-dimensional Euclidian orthogonal space, 001 by a vertex with space coordinates (0,0,1), and so on for the remaining code words 010, 100, 011, 110, 101, 111; the eight vertices span a 3-cube with edges between vertices differing in just one coordinate, such as between (0,0,0) and (0,0,1). This binary Hamming cube is shown in Figure 3. Vertices representing code words at Hamming 1-distance (1-HD), such as 000 and 001, are incident on the same edge (at 1-edge distance) and at Euclidian 1-distance (1-ED), while vertices representing words at Hamming 2- and 3-distance are respectively at 2- and 3-edge distances and at Euclidian √2- and √3-distance. Hamming distances are preserved in the cube model: they are mapped one-to-one onto Euclidian distances: 1-HD → 1-ED, 2-HD → √2-ED, and 3-HD → √3-ED. All n-bit binary codes can be mapped to n-cubes this way; e.g., the 64 (=2⁶) 6-bit binary words to a 6-cube with 192 (=64 × 6/2) edges connecting vertices representing words at 1-Hamming distance (each vertex is incident on six edges; each code word is at 1-HD of six other words.) Hamming distances and their geometric representation are basics tools of mathematical code analysis, with, among others, relevance to a code’s error detection and correction capacities [9]. Hamming’s cube model has inspired similar models for the genetic code, but importantly the genetic code is quaternary—it uses four symbols, {A, C, G, U}, and not binary—{0,1}. This has implications for the geometric model of the code that hitherto have not been recognized to the best knowledge of this author.

Figure 1. The standard codon table. The table orders the 64 codons into 16 blocks of four codons varying at the third position only—the family boxes. The nucleotides are ordered as in (U, C, A, G). The rows are in this order by the first, the columns by the second, and the blocks by third codon position. The 64 slots each contain a codon and the message encoded by this codon, an amino acid or stop signal. The stop codon slots are white; the amino acid slots are colored with the color code for the Polar Requirement of the amino acid shown in Figure 2.

Figure 2. The Polar Requirements of 20 amino acids. Polar Requirement (PR) values for the 20 amino acids encoded by the canonical genetic code are listed by increasing value and color coded by a gradation of rainbow colors. Hydrophobic amino acids have PRs less than the PR of Ser and are colored with the purple to blue values, while hydrophilic amino acids have PRs greater than the PR of Ser and are colored with green to yellow and orange values.

Figure 3. The Hamming 3-cube. The Hamming 3-cube is the geometric model for the 8-word, 3-length binary code, the Euclidian vertex coordinates correspond with the code words as indicated in the figure.

Various mathematical models of the genetic code have been published. Many models ([12,13,14,15,16] and references herein) use one of the 24 mappings of the four common nucleotides to 2-bit binary codes, such as (U, A, G, C) → (00, 10, 01, 11), so that codons are represented by 6-bit binary words. Importantly, these mappings do not preserve the genetic code’s Hamming distances: 1-distances due to different nucleotides at the same codon position become either 1- or 2-distances in binary. To witness: the U-A, U-G, A-C and G-C nucleotide-to-nucleotide 1-distances map to binary 1-distances between, respectively, 00–10, 00–01, 10–11 and 01–11 (only one binary bit differs), while the U-C and A-G nucleotide 1-distances map to binary 2-distances between, respectively, 00–11 and 10–01 (both bits differ). The geometric model of this binary code is the Hamming 6-cube spanned by 64 vertices corresponding with the 64, 6-bit binary words representing the codons [17,18,19]. In the 6-cube every 6-bit word has six nearest neighbors—not nine as in the genetic code, and the cube’s 192 length-1 edges correspond with the 192 binary Hamming 1-distances between the 64 6-bit words, but there are actually 288 Hamming 1-distances between the 64 codons, see Section 2.3. Other mathematical models ignore the Hamming metric, but assume that the 64 codons form a mathematical group and analyze the code based on a quantum crystal basis [20], or based on 64 dimensional irreducible representations of Lie groups [21,22] or finite groups [23]. These group theoretical approaches are motivated by their successes in, among others, quantum and particle physics and by the thesis that breaking the code-group into smaller subgroups models the code’s evolution and explains its degeneracy patterns.

Our geometric model, a 9-polytope differs significantly from the 6-cube and the other mathematical models for the genetic code referenced above, but the polytope does uniquely correspond with the graph representation of the codon set with Hamming metric, the CodonGraph (Section 2.3, [24]). The symmetry group of the CodonPolytope is isomorphic to a product of small permutation groups acting on the codon set and to the symmetry group of the CodonGraph (Section 4 and Section 5). However the polytope symmetry group is very different from the 6-cube group and other mathematical groups mentioned above. Many Euclidian symmetries of the polytope correspond with the similarity and degeneracy patterns of the genetic code, in other words, these polytope symmetries identify code symmetries (Section 6). The lower dimensional faces of the polytope display the strongest code symmetries and this hierarchy of face symmetries suggests that the early evolution of the code in pre-LUCA organisms can be modeled by splitting the polytope progressively into its lower dimensional faces. This model evolves the characteristic symmetry patterns of the code, patterns most unlikely generated by random processes (Section 6). An accurate geometric model for the genetic code can form the basis for further mathematical analysis. To illustrate: we applied Polya’s colorings enumeration to count the number of code (=colorings) classes. The polytope symmetries partition the astronomically large number of all possible codes mapping 64 codons onto 21 messages into symmetry equivalence classes. This classification quantifies the uniqueness of the genetic code and its symmetries (Section 7). These findings and applications of the CodonPolytope for the analysis of the genetic code are discussed (Section 8).

2. Preliminaries

This section summarizes some essential, well known, as well as some lesser known, but previously published background material for this article. The appendices contain some mathematical background material; Section 3 ,Section 4, Section 5, Section 6, and Section 7 cover the new, original results.

2.1. The Code Function

The canonical genetic code is comprised of 64 codons, triplets of the nucleic acid bases Adenine, Cytosine, Guanine or Uracil, abbreviated as A, C, G, and U, located on messenger RNA strands (on DNA, Thymine replaces Uracil). In the language of mathematical coding theory [9] the codons correspond with code words; the codons are all 64 (=4³) three-letter code words that can be made up by the four letter alphabet {A, C, G, U}. The genetic code is a length-3 block code—all code words have the same 3-length, and it is a quaternary code—build with four symbols, as opposed to the more common binary computer codes constructed with two symbols {0,1}. Each code word encodes a single message, an amino acid or stop signal, as reflected in the standard codon table (see Figure 1). The code function C: 64 codons → 21 messages is an onto mapping, or surjection, that reaches all 21 target messages at least once, but this coding function is not a bijection as several codons map to the same message, i.e., the function C is not invertible. The encoding of the same message by different (synonymous) codons is known by biologists as the degeneracy of the code. Degeneracy is not identical with the coding theory notion of redundancy, which relates to code words that are longer than minimally required, say length-3 instead of length-2 blocks. The code is not redundant in this sense as a 4-letter length-2 block code can encode at most 16 (=4²) messages, not 21. We use [n] as notation for a finite n-set = {1, 2, …, n} so that the codons can be indexed (numbered) by [64] = {1, …, 64} and the messages by [21]. The genetic code is one of 1.51 × 1084 different [64] → [21] surjections, an astronomically large function space [24]. (Appendix A summarizes the notation and combinatorial counting formulas used in this article, see [25]) The fact that just one code (or at most a few, very similar codes) evolved is a strong argument in favor of a last unique common ancestor (LUCA) for all known living organisms, but how, pre-LUCA, this unique code evolved is a yet unanswered question.

2.2. The Hamming Distances between the 64 Codons of the Codon Set

Hamming distances, which equal the number of non-identical positions in code words, measure differences between code words: two different codons are at 1-, 2- or 3-Hamming distance. For example, the codons AAG, AAU are at 1-distance as they differ only in the third codon position, GAU, CAC at 2-distance, and GGG, ACU at 3-distance. Every codon is at 1-distance of nine other codons, at 2-distance of 27 other codons and at 3-distance of the remaining 27 codons of the codon set; the distances between the 64 codons are shown in Figure 4, the Codon-Distance-Matrix. The symmetry patterns of this matrix reflect the mathematical structure imposed on the codon set by the Hamming metric, the structure of the normed metric codon space. The Hamming distances are fundamental in mathematical coding theory, but also have significant biological relevance. They are related to mutation distances: A single point mutation changes a codon to a codon at 1-distance, and minimally two, respectively, three point mutations are required to change a codon to a codon at 2- or 3-distance. Hamming distances also are correlated with the code’s similarity patterns: Codons encoding the same message almost always are at 1-distance, and codons for similar messages most often are at 1- or 2-distance. For example, the four synonymous GUN codons (with N representing any of the four bases), each at 1-distance from the three others, make up the family box of the codon table encoding the hydrophobic amino acid valine. In addition these valine codons are at 1- or 2-distance of similar sets of synonymous codons encoding other hydrophobic amino acids: alanine (GCN), leucine(CUN, UUR), phenylalanine (UUY), isoleucine (AUA, AUY), and methionine (AUG)—with R representing a purine {A, G} and Y a pyrimidine {C, U} base (see Figure 1).

2.3. The CodonGraph, a Graph Representation of the Codon Set with Hamming Metric

A graph (G) is a set of vertices (V) together with a set of edges (E) between two vertices, elements of V:G = {V, E}, for V = {v₁, v₂, … , v_n} and E = {{v_i,v_j}, … , {v_x,v_y}}. Two vertices incident on the same edge are adjacent. The CodonGraph is comprised of 64 vertices, representing the codons, and 288 edges between adjacent vertices [24]. Adjacent vertices represent codons at Hamming 1-distance, and the graph is 9-regular as each vertex is adjacent to nine vertices representing the nine nearest neighbor codons at 1-distance. Therefore the graph contains 288 edges (288 = 64 × 9/2, two vertices per edge). Each vertex is connected via nine, 1-edge shortest paths with nine adjacent vertices, via 27, 2-edge shortest paths with 27 vertices representing codons at Hamming 2-distance, and via 27, 3-edge shortest paths with the remaining 27 vertices representing codons at Hamming 3-distance. The graph’s edge-metric (the number of edges on the shortest path) thus corresponds one-to-one with the Hamming metric: the graph representation of the codon set preserves the intercodon Hamming distances. Figure 5 shows a circular embedding of the CodonGraph—all vertices are arranged on a circle, numbered counterclockwise, and labeled with the codons in lexicographical order. A subgraph of the CodonGraph induced by a single vertex (such as vertex-1, AAA in Figure 6) comprises its nine adjacent vertices and contains three K4-graphs—complete-4 graphs made up of four adjacent vertices and six edges. The single induction vertex (vertex-1) is a cut vertex that connects the three K4-graphs (deleting this vertex disconnects the graph, cuts it in separate pieces). Each K4-graph contains four vertices that represent four codons that only differ at one particular codon position; for example, the vertices representing the codons AAA, AAC, AAG and AAU make up a K4-graph in Figure 6. Each of the 64 graph vertices and its nine adjacent vertices form a closed neighborhood made up of three K4-graphs as shown in Figure 6 (only the vertex labels change). Vertices connected via respectively 2- and 3-edge shortest paths are diagonal opposites of square- and cube-subgraphs—graph representations of the eponymous geometric figures, as shown in Figure 7. The CodonGraph has 3-width—the shortest path between any two vertices contains at most three edges, and the subgraphs of Figure 5, Figure 6 and Figure 7 thus illustrate all intercodon Hamming distance relationships.

Figure 4. The CodonDistanceMatrix. This 64 × 64 matrix shows the Hamming distances between the 64 codons numbered as in Figure 5. Zero-, 1-, 2- and 3-distances between codon-i (=row-i) and codon-j (=column-j) correspond with, respectively, black, dark gray, light gray, and white (small square) matrix entries-(i,j). Distance-0 entries (black) fall on the main diagonal, distance-1 (dark gray) entries correspond with edges between vertices i and j of the CodonGraph (Figure 5). Each row/column contains one 0-distance; nine 1-distances; 27, 2-distances; and 27, 3-distances [24].

Figure 5. Circular embedding of the CodonGraph. The graph’s 64 vertices are numbered and labeled counterclockwise with codons in lexicographical order and its 288 edges connect adjacent vertices at representing codons at Hamming 1-distance [24].

Figure 6. The closed neighborhood of vertex-1 of the CodonGraph. The subgraph of the CodonGraph induced by vertex-1 AAA and its nine adjacent vertices consists of three K4-graphs linked by cut vertex-1. The vertices are numbered and labeled as in Figure 5. Apart from the numbers and labels, the closed neighborhoods of all 64 vertices of the CodonGraph are identical [24].

Figure 7. A cube subgraph of the CodonGraph. The cube-graph shows that vertices representing codons at Hamming 2- and 3-distances are diagonal opposites of, respectively, square- and cube-subgraphs of the CodonGraph. For example, codons 50 = UAC and 58 = UGC are, respectively, at 2- and 3-distance of codon 1 = AAA. The vertices are labeled as in Figure 5 [24].

2.4. From Graph to Geometry

A graph represents a geometrical object if the vertex and edge sets of the graph correspond one-to-one with those of the object. For example, the cube-graph of Figure 7 obviously represents a geometrical cube. A graph can represent different geometries because edge-length and angles between edges are not defined in the graph, but they are in Euclidian space. For example, a square-graph represents all geometric quadrilaterals, including those with four unequal edges and four different interior angles; the four vertices need not lie in the same plane—the quadrilateral need not be flat. However, a triangle is always flat because three vertices always lay in a plane, and a K4-graph (four vertices and six edges; Figure 6 contains three K4-graphs) always represents a 3-dimensional tetrahedron with four flat triangular sides (otherwise the object has two “interior edges” and is a quadrilateral with four, not six edges).

The CodonGraph thus represents a geometric object with 64 vertices and 288 edges, a polytope. Importantly the edges of the polytope have to be congruent (of equal length) because in the graph as well as in Euclidian space, two codons at one Hamming distance (HD) are represented by adjacent vertices—vertices incident on the same edge: 1-HD thus corresponds with the Euclidian length of an edge of the polytope. Therefore the three K4-graphs of Figure 6 represent three congruent regular tetrahedrons, and the faces of these tetrahedrons are congruent equilateral triangles. The four vertices of a tetrahedron represent four codons differing in one position only, such as AAA, AAC, AAG and AAU—the four codons of a codon table family box. Surprisingly the existing genetic code literature contains square and rectangle models for the four nucleotides (as will be discussed in Section 8), but not this tetrahedron model. The polytope contains 48 regular tetrahedrons (as each vertex is incident on three tetrahedrons: 48 = 64 × 3/4) and 192 equilateral triangles (as each vertex is incident on nine triangles: 192 = 64 × 9/3 as shown in Figure 6 for vertex AAA), and it will be constructed in Section 4.1. The polytope cannot be a hypercube because an n-cube does not contain tetrahedrons or triangles, only cubes (a square is a 2-cube, an edge a 1-cube, and a vertex a 0-cube in this geometric analysis).

2.5. Permutation Symmetries of Graphs and Euclidian Symmetries of Geometric Objects

Symmetry, permutations and mathematical groups are fundamental concepts discussed in some detail in Appendix B. To briefly illustrate: the equilateral triangle (Figure 8) possesses three mirrors (μ1, μ2, μ3), and a single rotation axis (for 0, 120 and 240 degree rotations) perpendicular to its geometrical center; these six symmetries make up the symmetry group D3 (dihedral-3). The three mirrors intersect with 60 and 120 degree angles and two consecutive mirror reflections generate a rotation of twice the angle between the mirrors, so all symmetries can be generated by the mirrors: D3 is a reflection symmetry group. The geometric center is a unique point, fixed by all symmetries: D3 is also a point symmetry group [26]. D3 is isomorphic to S₃, the Symmetric group that contains all six permutations of three points, such as the three vertices of the triangle. (Isomorphic groups are essentially the same group, identical to abstract groups of the same number of group elements and their composition.) The mirror and rotation symmetries leave the triangle invariant—in the same position in the plane, but induce permutations of the triangle vertices that correspond with those of S₃. Similarly, the symmetry group of a triangle graph ({v₁, v₂, v₃}, {{v₁,v₂}, {v₁,v₃}, {v₂,v₃}}) permutes the three vertices {v₁, v₂, v₃}, and because all six permutations leave the edge set {{v₁,v₂}, {v₁,v₃}, {v₂,v₃}}invariant, this group is also isomorphic to S₃.

Figure 8. Equilateral triangle with mirrors. The vertices of the triangle are numbered (1, 2, 3) and the mirrors are labeled μ1, μ2, and μ3. The mirrors are incident on one vertex and orthogonally bisect the opposite side; they usually are seen as 2-dimensional planes perpendicular to the plane containing the triangle. Reflections in the three mirrors generate the D3 group of six symmetries.

As for the triangle, the symmetries of a regular tetrahedron are all mathematical transformations, such as rotations along an axis and reflections in a mirror plane, that leave it invariant—in the same position before and after the transformation; only if the object were labeled, as in Figure 9, could one observe that the object was transformed. To illustrate, Figure 9 shows a tetrahedron inscribed in a cube with a mirror plane incident on the {1, 2} edge and perpendicularly bisecting the {3, 4} edge. A reflection in this plane exchanges the vertices G ↔ U, i.e., maps ACGU → ACUG, but leaves the tetrahedron invariant (only the vertex labels changed places, but the labels are not part of the tetrahedron as geometric object). The tetrahedron has six mirror planes, each one bisecting a different edge, and all 24 symmetries of the tetrahedron are generated by reflections in these mirrors as detailed in Appendix C. These 24 symmetries form a reflection symmetry group, the Coxeter-A3 group [27] that is irreducible (not a product of smaller reflection groups) and characterizes, among others, the symmetries of methane (CH₄) with a central carbon and four hydrogen atoms at the vertices of a tetrahedron. The A3-group is isomorphic with the permutation group S₄, the Symmetric group on four objects, such as {A, C, G, U}, comprising all 24 permutations of these objects (Appendix B and Appendix C). The symmetry group of the K4-graph (Figure 6) of order 24 (the number of group elements) permutes the graph’s four vertices, but leaves its vertex and edge sets invariant and is isomorphic to both S₄ and A3 (isomorphism is transitive: if a ≈ b and b ≈ c then a ≈ c).

Figure 9. Tetrahedron inscribed in a cube with a mirror plane. The vertices of the tetrahedron are numbered (1, 2, 3, 4) and labeled (A, C, G, U). The front face is colored dark grey and the frontal edges are bold-solid-black while the edges hidden behind the front are bold-dashed-black. The edges of the cube are thin-gray-dashed. One of the six mirror planes of the tetrahedron is colored light-gray and outlined in thin-black. All six mirrors are planes intersecting the cube diagonally; reflections in these mirrors generate the Coxeter A3 group of 24 symmetries.

3. The CodonArray Embedding of the CodonGraph

The CodonArray, a not previously described embedding of the CodonGraph (Section 2.3), facilitates computation of the 3376 subgraphs and their corresponding faces of the geometric model, the CodonPolytope (Section 4). The graph’s 3-dimensional array embedding, projected as a 2D-image in Figure 10, is not a geometric model (most certainly not a cube). In the CodonArray the 64 vertices are organized as a 4 × 4 × 4 array with three array indices (i, j, k) that run over {1, 2, 3, 4} and identify each vertex by three “orthogonal” coordinates; e.g., i = 3, j = 2 and k = 4 identify vertex (3, 2, 4). Setting the indices (i, j, k) to correspond with codon positions (1, 2, 3) and by varying them in alphabetical order over {A, C, G, U} assigns codon labels to the array vertices; e.g., vertex (3, 2, 4) = GCU. Every row/column comprises four vertices and six edges and corresponds with a K4-graph (see Figure 11). Every vertex is incident on three orthogonal rows, and per row the labeling at only one codon position varies while the other two are fixed—identical to the neighborhood configuration for the cut index in Figure 6. For example, in Figure 10, vertex (1, 1, 1) = AAA is incident on three rows, labeled like the corresponding K4-graphs of Figure 6. With six edges per row, the 48 rows and columns (16 in each of the three orthogonal dimensions i, j, and k) contain all 288 edges of the CodonArray. Sub-arrays comprised of edge-connected vertices correspond with subgraphs; for example, a 4 × 1 × 1 subarray (a row of four vertices: one index varies over all four values, the other two indices are fixed at one value) corresponds with a K4-graph, and a 2 × 2 × 2 subarray (for any two values of the three indices) with a cube-graph. All 3376 subgraphs are identified and enumerated in Table 1. (To illustrate: the graph contains 216 = 6³ cube-graphs as there are C(4,2) = 6 ways to pick two from four values for each of the three indices, see Appendix A).

Figure 10. The CodonArray embedding of the CodonGraph. The CodonArray is a 3-dimensional 4 × 4 × 4 array embedding of the 64 vertices of the CodonGraph; it is a graph, not a Euclidian cube. Only some vertices are labeled and only three of the six edges per row/column are shown so as not to clutter the image.

Figure 11. A row/column K4-subgraph of the CodonArray. The K4-graph contains four vertices, shown as disks labeled 1, 2, 3 and 4, and six edges, and it corresponds with a single row or column of the CodonArray of Figure 10. Each K4 graph represents a tetrahedron (Figure 9).

Table 1. The 3376 subgraphs of the CodonGraph and faces of the CodonPolytope. The subgraphs correspond with subarrays of the 4 × 4 × 4 CodonArray, and each subgraph corresponds with a face of the CodonPolytope. The number of vertices and edges of each subarray is listed; the dimensions are the dimensions of the corresponding polytope faces, and the number of faces corresponds with the number of subarrays. Non-congruent faces of the same dimension are distinguished by proper names (Triangle versus Square) or capital letters (4A-Face versus 4B-Face). Subarray A × B × C stands for all permutations of A, B and C as their order does not matter: e.g., 4 × 1 × 1 = 1 × 4 × 1 = 1 × 1 × 4.

**Table 1.** The 3376 subgraphs of the CodonGraph and faces of the CodonPolytope. The subgraphs correspond with subarrays of the 4 × 4 × 4 CodonArray, and each subgraph corresponds with a face of the CodonPolytope. The number of vertices and edges of each subarray is listed; the dimensions are the dimensions of the corresponding polytope faces, and the number of faces corresponds with the number of subarrays. Non-congruent faces of the same dimension are distinguished by proper names (Triangle versus Square) or capital letters (4A-Face versus 4B-Face). Subarray A × B × C stands for all permutations of A, B and C as their order does not matter: e.g., 4 × 1 × 1 = 1 × 4 × 1 = 1 × 1 × 4.
Sub-Arrays of the CodonArray and the corresponding Faces of the CodonPolytope
Dimension	Sub-Array	Face Name	Vertices	Edges	Faces	Faces per Dimension
9	4 × 4 × 4	Polytope	64	288	1	1
8	4 × 4× 3	8-Facet	48	192	12	12
7	4 × 4 × 2	7A-Ridge	32	112	18	66
7	4 × 3 × 3	7B-Ridge	36	126	48	66
6	4 × 4 × 1	6A-Face	16	48	12
	4 × 3 × 2	6B-Face	24	72	144
	3 × 3 × 3	6C-Face	27	81	64	220
5	4 × 3 × 1	5A-Face	12	30	96
	4 × 2 × 2	5B-Face	16	40	108
	3 × 3 × 2	5C-Face	18	45	288	492
4	4 × 2 × 1	4A-Face	8	16	144
	3 × 3 × 1	4B-Face	9	18	192
	3 × 2 × 2	4C-Face	12	24	432	768
3	4 × 1 × 1	Tetrahedron	4	6	48
	3 × 2 × 1	Prism	6	9	576
	2 × 2 × 2	Cube	8	12	216	840
2	3 × 1 × 1	Triangle	3	3	192
2	2 × 2 × 1	Square	4	4	432	624
1	2 × 1 × 1	Edge	2	1	288	288
0	1 × 1 × 1	Vertex	1	0	64	64
−1	0 × 0 × 0	Empty	0	0	1	1

4. The Geometric Model: The CodonPolytope

4.1. The Construction and Characterization of the CodonPolytope

Recall the regular tetrahedron, one of the Platonic solids; it has four vertices, six equal-length edges and four congruent, equilateral triangular faces. (The four faces, which lie in four 2-dimensional planes are the boundaries that close the 3-dimensional tetrahedron.) Number the tetrahedron vertices (1, 2, 3, 4), label them (A, C, G, U) so that an edge and its geometric Euclidian length represents the Hamming 1-distance between two words of a quaternary length-1 block code as shown in Figure 9. The tetrahedron is a 3-dimensional geometric object, a polyhedron, an object closed by its faces. Polytopes are closed geometric objects of any dimension: Line segments are 1-polytopes (closed by two endpoints), polygons, such as a triangle, 2-polytopes (closed by line segments), polyhedrons 3-polytopes, and d-dimensional closed geometric objects d-polytopes. Higher dimensional polytopes can be constructed from lower dimensional ones by the polytope product [28,29], a procedure detailed in Appendix D. For example, the product of two congruent line segments gives a square, and of three such line segments in a cube, etc. The CodonPolytope is the polytope product of three congruent regular tetrahedrons (Th), indexed 1, 2, and 3: Th₁ × Th₂ × Th₃. The Cartesian product of the vertex sets of the three tetrahedrons produces the 64 (=4³) vertices of the polytope. When labeled as above (Figure 9), the vertices of the CodonPolytope are numbered and labeled like those of the CodonArray graph. For example, the product of vertex-3 of Th₁, vertex-2 of Th₂ and vertex-4 of Th₃ generates polytope vertex (3,2,4) = GCU. By construction every polytope vertex is incident on three tetrahedrons and connected via nine equal-length edges with nine adjacent vertices. This geometry corresponds with the closed neighborhood of the CodonGraph vertices, which are incident on three K4-graphs (Figure 6 and Figure 10). Therefore the vertex and edge sets of the CodonPolytope and CodonGraph correspond one-to-one: the graph uniquely represents the polytope—any graph representing the polytope is isomorphic to the CodonGraph. (Section 2.4. discusses the relation between a graph and the geometric objects it represents).

The CodonPolytope is a simple 9-polytope: 9-dimensional as the polytope product sums the dimensions of the three tetrahedrons, and simple because its dimension equals the number of edges on which every vertex is incident. A theorem by Blind and Mani states that simple polytopes are determined, up to combinatorial isomorphism, by their graphs [29]. This means that the number of faces of all dimensions and their relations, the face lattice of the polytope, is fully determined by the graph, but of course the graph does not define the Euclidian angles and scale of the polytope. In this sense, the CodonPolytope is the unique geometric representation of the CodonGraph. All 3376 polytope faces and corresponding graphs (sub-arrays of the CodonArray) are enumerated in Table 1. The 9-polytope is the highest, 9-dimensional face, the 8-facets are 8-dimensionsal faces, the 7-ridges 7-dimensional faces, and so on. The empty face corresponds with the empty vertex set and by convention has dimension minus-one. Non-congruent polytope faces of the same dimension, such as the 2-dimensional triangles and squares, are, when they lack proper names, distinguished by capital letters, such as for the 4-dimensional faces: 4A, 4B, and 4C. Because the CodonPolytope contains such incongruent faces of same dimension, it is not regular (unlike an n-cube, which is regular as its proper faces are all congruent cubes of lower dimensions). The dimension of the faces corresponds with the dimension of the polytope product of the corresponding subarrays; for example, the 4 × 3 × 2 subarray corresponds with the product of a tetrahedron, triangle and line segment respectively, and the sum of their dimensions is 6 (3 + 2 + 1). All subarrays correspond with polytope products of simplexes—geometric objects of dimension one less than their number of vertices, and all polytope faces thus are simple polytopes. Table 1 is summarized by the face-vector of the polytope, which lists the number of faces per dimension starting with the lowest dimension, empty face: (1, 64, 288, 624, 840, 768, 492, 220, 66, 12, 1). Because the tetrahedron is closed and convex (any line segment connecting two points of the tetrahedron lies entirely within the tetrahedron), the polytope, by construction, is also closed and convex, and as a solid, or closed point set, equals the convex hull of its 64 vertices, just as the tetrahedron equals the convex hull of its four vertices. (A convex hull is the “shrink wrapped” space enclosed by the vertices.) The polytope is closed by its 12, 8-facets, which lie in 12 different 8-D hyperplanes. The Euler-Pointcaré characteristic, the alternating sum of the face-vector equals zero for convex polytopes [29] and indeed: 1 + 64 – 288 + 624 – 840 + 768 – 492 + 220 – 66 + 12 − 1 = 0. (This formula generalizes Euler’s famous V – E + F = 2 sum of vertices, edges and faces for convex polyhedrons). Simple polytopes have interesting “twins” named polar or dual polytopes, such as the well-known cube and octahedron duals—twinning Platonic solids. The dual of the simple CodonPolytope is a unique polar simplicial 9-polytope, the CodonPolar, which is described in detail in Appendix E. All CodonPolar faces are enumerated in Table 2; they correspond via an inversion of the face vector and an anti-isomorphism of the face lattice one-to-one to the CodonPolytope faces. In particular, the CodonPolar possesses 64 congruent 8-facets in one-to-one correspondence with the 64 vertices of the CodonPolytope, and thus with the 64 codons: the CodonPolar is a 9-dimensional 64-sided die that, in a figurative sense, can be cast to randomly pick with equal probability any of the 64 codons.

Table 2. The 3376 faces of the Codon-Polar-Polytope. The 12 vertices of the polytope are located on three tetrahedrons, each residing in a different 3-dimensional subspace of a Euclidian 9-space. The notation P + Q + R stands for P-, Q-, and R-vertices on the different tetrahedrons; e.g., each of the vertices of a 1 + 1 + 1 A-Triangle is incident on a different tetrahedron, while those of a 3 + 0 + 0 C-Triangle are all incident on the same tetrahedron.

**Table 2.** The 3376 faces of the Codon-Polar-Polytope. The 12 vertices of the polytope are located on three tetrahedrons, each residing in a different 3-dimensional subspace of a Euclidian 9-space. The notation P + Q + R stands for P-, Q-, and R-vertices on the different tetrahedrons; e.g., each of the vertices of a 1 + 1 + 1 A-Triangle is incident on a different tetrahedron, while those of a 3 + 0 + 0 C-Triangle are all incident on the same tetrahedron.
Faces of the Codon-Polar-Polytope
Dimension	Vertex sets	Face Name	Vertices	Edges	Faces	Faces per Dimension
9	4 + 4 + 4	PolarPolytope	12	66	1	1
8	3 + 3 + 3	8-Facet	9	36	64	64
7	3 + 3 + 2	7-Ridge	8	28	288	288
6	3 + 2 + 2	6A-Face	7	21	432
6	3 + 3 + 1	6B-Face	7	21	192	624
5	2 + 2 + 2	5A-Face	6	15	216
	3 + 2 + 1	5B-Face	6	15	576
	3 + 3 + 0	5C-Face	6	15	48	840
4	2 + 2 + 1	4A-Face	5	10	432
	3 + 1 + 1	4B-Face	5	10	192
	3 + 2 + 0	4C-Face	5	10	144	768
3	2 + 1 + 1	A-Tetrahedron	4	6	288
	2 + 2 + 0	B-Tetrahedron	4	6	108
	3 + 1 + 0	C-Tetrahedron	4	6	96	492
2	1 + 1 + 1	A-Triangle	3	3	64
	2 + 1 + 0	B-Triangle	3	3	144
	3 + 0 + 0	C-Triangle	3	3	12	220
1	1 + 1 + 0	A-Edge	2	1	48
1	2 + 0 + 0	B-Edge	2	1	18	66
0	1 + 0 + 0	Vertex	1	0	12	12
−1	0 + 0 + 0	Empty	0	0	1	1

4.2. A Realization of the CodonPolytope

The CodonPolytope can be realized in Euclidian 9-space: Three 3D-tetrahedrons, centered on the origin, their vertices numbered (1, 2, 3, 4), labeled (A, C, G, U), and assigned space coordinates (1,1,1), (−1,−1,1), (1,−1,−1), (−1,1,−1) generate, via the Th₁ × Th₂ × Th₃ product, 64 vertices with 9-space coordinates—concatenations of the relevant sets of 3-space coordinates. To illustrate, polytope vertex (3,2,4) = GCU has coordinates (1,−1,−1,−1,−1,1,−1,1,−1). The realized polytope is centered on the origin of the 9-space, and all its vertices are located on an 8-sphere surface at Euclidian 3-distance from the origin (√(1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1) = √9 for all vertices). The Hamming 1-, 2- and 3-distances between the codon labels of the vertices are in one-to-one correspondence with the Euclidian distances 2√2, 4 and 2√6 between vertices and with one, two, or three edges on the shortest path between vertices. These mappings of the intercodon Hamming distances onto the polytope are well defined and invertible, and thus preserve the Hamming metrics of the code. The polytope is inscribed in a 9-cube with 512 (=2⁹) vertices that have space coordinates composed of nine ±1 entries. Only one out of eight cube vertices coincides with a polytope vertex.

4.3. The Point Symmetry Group of the CodonPolytope

Section 2.5 discusses the symmetry groups of triangle—D3, and the tetrahedron—the Coxeter-A3 group, and their isomorphism to the permutation groups S₃ and S₄ respectively.

The symmetries of the CodonPolytope are all orthogonal transformations of the Euclidian 9-space that leave the polytope invariant. These rotations and reflections form a point group that fixes the unique geometric center point of the polytope and maps the polytope vertex set onto itself. By construction of the CodonPolytope as rectangular product of three tetrahedrons (Section 4.1), the direct product of three Coxeter-A3 groups, A3 × A3 × A3, becomes a symmetry group of the 9-polytope. Each A3-group acts on a different 3-subspace and fixes the complementary perpendicular 6-space. We index the groups: A3₁ acts on the 3-subspace spanned by dimensions 1, 2 and 3; A3₂ on the space spanned by dimensions 4, 5 and 6; and A3₃ on the space spanned by dimensions 7, 8 and 9. Their 18 mirror planes (3 × 6 per tetrahedron), which are 8-dimensional hyperplanes dividing the 9-space into two 9-dimensional half spaces, generate all 13,824 (24³) polytope symmetries of A3₁ × A3₂ × A3₃. Each mirror bisects 16 polytope edges and exchanges the 32 vertices incident on these edges, but does not move the other 32 vertices as they lie within the 8-plane. For example, one mirror fixes all 32 {NNA, NNC} (N stands for any letter), but exchanges all 32 other codon labels, NNG ↔ NNU, analogous to the tetrahedron G ↔ U mirror shown in Figure 9. All 18 edges of the three tetrahedrons in Figure 6 (represented by K4 graphs) are bisected by one of the 18 mirrors, e.g., mirror NNG ↔ NNU bisects {AAG, AAU}, but fixes all other vertices of Figure 6. The six mirrors of each A3 are perpendicular to the mirrors of the other two groups so that reflections of different A3 groups commute, e.g., the order of multiplication of A3₁ × A3₂ × A3₃, the direct product of the three A3 symmetry groups, does not matter. The three A3 groups are identical as are the three 3D-subspaces on which they act. Six transformations (3 rotations, including the 0-degree identity rotation, and three reflections) exchange these 3D-subspaces and form a 9-dimensional reflection group isomorphic to D3, the symmetry group of the equilateral triangle. These transformations exchange the six tetrahedron mirror planes between the three 3D-subspaces, and thus exchange or permute the three A3 groups. The symmetry group of the CodonPolytope thus is formed by the product of the 9-dimensional reflection group isomorphic to D3 with the direct product of the three A3 groups. This space symmetry group is isomorphic to the permutation group formed by the wreath product of S₃ with the direct product of three S₄ groups: S₃ x_wreath (S₄)₁ × (S₄)₂ × (S₄)₃—in this wreath product S₃ permutes the three S₄ groups (as described above for the three A3 groups), or equivalently the 4-sets upon which they act (analogous to the permutations of the 3D-subspaces mentioned above). The actions of the permutation group S₃ x_wreath (S₄)₁ × (S₄)₂ × (S₄)₃ on the codon set are described in Section 5.1 and Appendix B; for wreath products and permutation group theory see [30,31]. The CodonPolytope symmetry group has order 82,944 (=6 × 24³).

A matrix representation of this symmetry group is computed from scratch. The symmetry group of the polytope must be a subgroup of the group of all orthogonal transformations of Euclidian 9-space that leave the (infinite) set of points with nine integer coordinates in this space invariant—the modular orthogonal group O-(9, Z) of order 185,794,560 (=2⁹ × 9!) [32]. These transformations correspond with 9 × 9 matrices having only one non-zero ±1 entry per row and column (in particular, all 512 = 2⁹ vertices of a unit 9-cube with 9 ± 1 coordinates are permuted by these transformations). Only those matrices that map the set of coordinates of the 64 vertices of a realization of the polytope (Section 4.2) onto itself are symmetries of the polytope and a computer scan of the 185,794,560 matrices identified 82,944 such symmetries; one advantage of a geometric model is that it permits such brute experimental computation. These 82,944 matrices can be partitioned into six sets of similar block matrices, each matrix is composed of nine 3 × 3 blocks: three 3 × 3 blocks contain the 24 tetrahedron symmetries for the three 3D-subspaces (the A-entries) and six 3 × 3 blocks are zero matrices (the dot “.”-entries). These six matrix sets are:

(\begin{matrix} A & . & . \\ . & A & . \\ . & . & A \end{matrix})

,

(\begin{matrix} A & . & . \\ . & . & A \\ . & A & . \end{matrix})

,

(\begin{matrix} . & . & A \\ . & A & . \\ A & . & . \end{matrix})

,

(\begin{matrix} . & A & . \\ A & . & . \\ . & . & A \end{matrix}),

(\begin{matrix} . & A & . \\ . & . & A \\ A & . & . \end{matrix})

,

(\begin{matrix} . & . & A \\ A & . & . \\ . & A & . \end{matrix})

.

These six sets are generated from the first set by the six permutations of S₃ that exchange the 3 perpendicular 3-subspaces (replacing the A-blocks with 3 × 3 identity matrices corresponds with a matrix representation of S₃ in 9-space.) Each set of matrices comprises 13,824 (24³) symmetries, and the union of the six sets 82,944 symmetries. The matrix symmetry group of the CodonPolytope thus is a O-(9, Z)-subgroup with index 2240 (=2⁹ × 9!/82,944)—only one of every 2240 symmetries of O-(9, Z) is a symmetry of the polytope, but all 185,794,560 transformations of O-(9, Z) are symmetries of the unit 9-cube in which the polytope is inscribed.

For comparison: the symmetry group of the unit 6-cube, often used to model the codon set (see Section 1) equals O-(6, Z) and is isomorphic to S₆ x_wreath (S₂)⁶. This group has order 46,080 (=6! × 2⁶ = 720 × 64) and thus is smaller than the CodonPolytope symmetry group, but the 6-cube group is not a subgroup of the polytope group as its index 1.8 (= 82,944/46,080) is not an integer. S₃ x_wreath (S₂ × S₂)₁ × (S₂ × S₂)₂ × (S₂ × S₂)₃ of order 384 (=6 × 4³) is the largest group that the six cube and polytope groups have in common. Each S₂ permutes the two bits at one of the six-positions, each S₂ × S₂ is isomorphic to the Klein Four group, and the S₃ wreath product exchanges the 2-bit sets at positions {1,2}, {3,4}, and {5,6}—each set corresponds with a codon position. The S₂ × S₂ subgroup of S₄ corresponds with the three 180 degree rotations of the tetrahedron plus the 0 degree rotation identity of the A3 tetrahedron symmetry group (see Appendix C).

4.4. Symmetries of the Polytope Faces

The symmetry groups of the polytope faces are stabilizers or isotropy groups that map the vertex set spanning a face onto itself, and they are subgroups of the symmetry group of the polytope. Table 1 lists the faces as polytope products: 4 indicates a tetrahedron, 3 a triangle, 2 a line segment, and 1 a vertex. The stabilizer groups correspond with the (wreath) product of the symmetry groups of the faces in these polytope products. The tetrahedron group is isomorphic to S₄, the triangle group to S₃, the edge group to S₂, and the vertex group to S₁, which is usually omitted. As shown above, the 4 × 4 × 4 polytope is the product of three tetrahedrons and its stabilizer group is isomorphic to S₃ x_wreath (S₄)₁ × (S₄)₂ × (S₄)₃ (Section 4.3). Similarly the stabilizer of a 2 × 2 × 2 cube face is isomorphic to S₃ x_wreath (S₂)₁ × (S₂)₂ × (S₂)₃ of order 48 (=6 × 2³), which is isomorphic to the cube reflection symmetry group. And the stabilizer group of the 6-face corresponding with a 4 × 3 × 2 subarray is isomorphic to the direct product (S₄)₁ × (S₃)₂ × (S₂)₃ of order 288 (=24 × 6 × 2); this symmetry group lacks a wreath product permuting the three Symmetric groups because these groups are unequal; equivalently, the tetrahedron, triangle and line segment are not congruent and no Euclidian symmetry exchanges them.

5. The Symmetries of the CodonGraph and Codon Set

5.1. The Symmetries of the Codon Set That Preserve Hamming Distances

Recall the Coxeter A3 reflection symmetry group of the tetrahedron—a 3-dimensional geometric object; this group is isomorphic to the symmetry group of the K4-graph—a set of four vertices and six edges representing the tetrahedron, and both are isomorphic to S₄, which permutes four objects—just four points of zero dimension in an abstract point space in correspondence with the four vertices of the K4-graph or those of the tetrahedron (Section 4.3 and Appendix B and Appendix C). Similarly, the symmetry group of the CodonPolytope—a 9-dimensional geometric object, is isomorphic to the symmetry group of the CodonGraph—a set of 64 vertices and 288 edges, and both are isomorphic to the permutation group S₃ x_wreath (S₄)₁ × (S₄)₂ × (S₄)₃—the wreath product of S₃ with the direct product of three S₄ (Section 4.3). (Notation: the index-i for i = 1, 2, 3, in (S₄)_i corresponds with the codon position acted on by the S₄ group, and S₃ permutes the codon positions; See also Appendix B and [30,31].) Perhaps it is helpful to “visualize” this permutation group as the symmetry group of a (large) equilateral triangle with three congruent tetrahedrons, labeled 1, 2 and 3, centered on the vertices of this triangle: each tetrahedron is transformed independently of the two others by its own 24 symmetries in its own 3-space in correspondence with the actions of S₄ on the tetrahedron vertex labels {A, C, G, U}, and the tetrahedrons are exchanged by the six symmetries of the triangle in correspondence with the actions of S₃ on three S₄ groups. With the vertices of the triangle and the tetrahedrons labeled as in the Figure 8 and Figure 9, this configuration has 6 × 24 × 24 × 24 = 82,944 differently labeled, but identical geometries. Most importantly, as will be shown below, S₃ x_wreath (S₄)₁ × (S₄)₂ × (S₄)₃ acting on the codon space (64 points in an abstract point space with Hamming metric) preserves the Hamming metric: the Hamming distance between any two codons p, q є [64] is the same before and after any of the 82,944 permutations of the codon set induced by this group. The group induces two kinds of permutations of the 64 codons: the three S₄ permute the four letters at each of the three codon positions, and the S₃ wreath product permutes the three indices, or equivalently, the three codon positions (Appendix B). For example, the permutation (1,2,3,4) → (2,1,4,3) є S4 induces the permutation (A,C,G,U) → (C,A,U,G), and when acting at the middle codon position—e.g., as element of (S₄)₂, induces a permutation of all 64 codons: AAA ↔ ACA, AGA ↔ AUA, … etc., a reordering of the lexicographically ordered codons: (1, 2, 3, 4, 5, 6, …, 63, 64) → (2, 1, 4, 3, 6, 5, …, 64, 63), a [64] → [64] permutation of the codon set. Similarly the permutation (1,2,3) → (3,2,1) є S3 acting on the codon set exchanges the letters at the first and third codon position of all codons: AAA ↔ AAA, AAC ↔ CAA, CAG ↔ GAC, … etc., which also reorders the indexed codons. A basic theorem states that every permutation and Symmetric group can be generated from transpositions, or inversions—permutations exchanging two elements (a, b) → (b, a); the above (1,2,3) → (3,2,1) є S3 is a (1,3) → (3,1) inversion, and the (1,2,3,4) → (2,1,4,3) є S₄ contains two inversions. As can be readily checked the three inversions contained in S₃ and the six in S₄ induce permutations of the codon set that preserve the Hamming metric, and therefore all permutations generated by these inversions do as well, that is all of S₃ and S₄, and the 82,944 permutations of S₃ x_wreath (S₄)₁ × (S₄)₂ × (S₄)₃.

The largest permutation group acting on the codon set is S₆₄ and any inversion of S₆₄: (p, q) → (q, p) є S₆₄ for p, q є [64], affects just two codons—say, for p = 2 and q = 4: AAC ↔ AAU, which changes their intercodon Hamming distances with many fixed codons, with, for example, ACC and AUU (AAC and ACC are at 1-HD, but after the permutation AAC → AAU, AAU and ACC are at 2-HD). All 30 other codons ending with C or U have to undergo the same exchange to preserve the Hamming metric of the codon space, while the 32 codons ending in A or G can remain fixed, and the letters at codon positions 1 or 2 of all codons do not change (these findings are easily confirmed by experiment, or by a long proof by cases). Together these 16 inversions of S₆₄ preserve the Hamming metric, but their union is identical with the inversion (C, U) → (U, C) induced by (3, 4) → (4, 3) є (S₄)₃ acting on the codon set. Some inversions of S₆₄ (such as for p = 7 and q = 19: ACG ↔ CAG) result in letter changes in more than one codon position, and when complemented by the relevant 15 inversions at each position to preserve the Hamming metric, their union corresponds with an action of the S₄ groups acting at each codon position (as above). Alternatively in some cases, such as for ACG ↔ CAG, inversions of S₆₄ (that transpose codon positions 1 and 2) affecting all eight codons ACN ↔ CAN, but then also of the eight AGN ↔ GAN and eight UCN ↔ CUN codons, etc., can complement the initial inversion to preserve the Hamming metric, and their union then equals the inversion (1,2) → (2,1) є S3 acting on the codon set. (The above set of inversions of S₆₄ does not include any permutations of the 16 codons {AAN, CCN, GGN, UUN}, but the action of (1,2) → (2,1) є S3 on these codons also equals the identity, that is they remain fixed.) Thus a single inversion of S₆₄ acting on the codon space does not preserve the Hamming metric, but this inversion can be complemented with a set of similar inversions, the union of which preserves the metric, but then also equals one of the permutations of the codon set induced by an action of S₃ x_wreath (S₄)₁ × (S₄)₂ × (S₄)₃. This wreath product therefore contains all permutations of the codon set that preserve the intercodon Hamming distances; it is the largest subgroup of S₆₄ that does this. Both the wreath product of order 82,944 and the direct product (S₄)₁ × (S₄)₂ × (S₄)₃ of order 13,824 are transitive on the codon set—they permute any codon into any other; the orbit of each codon under these symmetry groups equals the whole set. Both groups are small subgroups of S₆₄ with integer index ≈9.18 × 10⁸⁴ and ≈1.53 × 10⁸⁴ respectively (the index equals the order of S₆₄/order of subgroup). S₆₄ contains all 64! (≈1.27 × 10⁸⁹) permutations of the codon set and permutations preserving the Hamming metric are relatively rare—only about 1 of every 10⁸³ permutations of the codon set does so.

5.2. The Symmetries of the CodonGraph

The symmetries of the CodonGraph are most easily derived by inspection of the CodonArray (Section 3), which looks like a 3-dimensional cube (Figure 10), but is a graph with six edges (not three edges) per row (Figure 11). The four values of the three indices (i, j, k) are permuted by the three S₄ groups. For example, the inversion (1,2,3,4) → (2,1,3,4) є S₄ acting on the values of index-j induces a relabeling of the graph’s vertices (A,C,G,U) → (C,A,G,U) that affects 32 codons with A or C at the middle position (i.e., AAA ↔ ACA): the 16 vertices of the front of the “cube” of Figure 10 (AAA to UAU) are exchanged with the 16 vertices right behind them (ACA to UCU), and this leaves the structure of the array intact (both the vertex and edge sets are invariant, only the labels changed.) The same holds for all such inversions for all three S₄ and thus for the direct product (S₄)_i × (S₄)_j × (S₄)_k. (Notation: the index-p with p = i, j, or k in (S₄)_p corresponds with the array index i, j, k acted on by the S₄ group.) The S₃ wreath product permutes the three indices (i, j, k), which is a symmetry of the CodonArray as the array is identical in each of these three directions. Inspection of the array reveals no other symmetries, and exchanging just one vertex (with edges attached) between different rows, requires readjustments of other vertices (with edges attached) like those described for codon inversions in Section 5.1 to restore the array. The symmetry group of the graph thus equals S₃ x_wreath (S₄)_i × (S₄)_j × (S₄)_k of order 82,944. (The CodonGraph symmetry group was derived in a different way in [24].) The graph symmetry group contains stabilizer subgroups for all its 3376 subgraphs; they are isomorphic to the stabilizer groups for the polytope faces, and easily derived from the subarrays, as discussed in Section 4.4. For example, the wreath product contains 216 (=6³) copies of S₃ x_wreath (S₂)_i × (S₂)_j × (S₂)_k—isomorphic to symmetry group of the cube, as each S₄ contains 6 S₂ subgroups; the 216 cube subgraphs are easily seen in the array (take any two vertices of each of the three orthogonal rows and “fill out” the cube). The graph symmetries permute the codon labels of the vertices of the array, and indeed, the array vertices can be labeled in 82,944 ways: Any of the 64 codons can be mapped to vertex (1,1,1), e.g., AAA → (1,1,1) as in Figure 10. This leaves nine labeling choices for a vertex at Hamming 1-distance of AAA, e.g., AAC → (1,1,2), which maps codon position-3 to array index-k and leaves only two choices for the remaining two letters in the third position, e.g., (AAG), (AAU) → (1,1,3), (1,1,4). Labeling one of remaining six vertices at 1-distance of (1,1,1) = AAA, e.g., ACA → (1,2,1), maps the two other codon positions to specific indices: 2 → j and 1 → i, and this restricts the labeling of the other five vertices to these two rows. In total 64 × (9 × 2 × 1) × (6 × 2 × 1) × (3 × 2 × 1) = 82,944 labeling choices—a confirmation of the order of the graph’s symmetry group. Without the array structure—the 288 edges between the 64 vertices in the 9-regular graph, the 64 vertices can be labeled in 64! ways, the number of [64] → [64] onto mappings of 64 labels onto 64 points.

6. Symmetries of the Genetic Code

6.1. Exact and Near Symmetries of the Code

The degeneracy of the genetic code—the encoding of the same message by different codons, and the symmetries of the CodonPolytope are related. For example, the familiar codon table (Figure 1) shows that codons UUU and UUC both encode Phe; indeed all 16, 2-codon sets {NNC, NNU} encode the same amino acid. (Notation: N stands for any nucleotide, but in comparisons between two or more sets N indicates the same nucleotide for the comparison, so that {NNC, NNU} indicates {AAC, AAU}, {ACC, ACU}, etc.) Thus the NNC ↔ NNU mirror (one of the 18 mirrors generating the direct product symmetry group of the polytope, Section 4.3), which induces the corresponding permutation of 32 codons, leaves the genetic code completely unchanged—invariant, and is an exact symmetry of the code. (A symmetry of a set of objects is a change—a transformation, imposed on the set that leaves some aspect of this set invariant; exact code symmetries leave the code invariant.) The NNC ↔ NNU permutation induces a reordering of the codons in 32 of the 64 slots of the codon table while the amino acid assignments of these slots are not altered—they are fixed as a reference frame, not affected by the permutation. For example, the codon in the top-left slot changes from UUU to UUC, but this slot remains assigned to Phe, and because UUU and UUC both encode Phe in the code, this permutation does not change the codon-amino acid assignment—it leaves the genetic code invariant. The NNA ↔ NNG mirror leaves the standard code invariant for 28 out of the 32 permuted codons and is thus a near symmetry of the standard code, but an exact symmetry of the mitochondrial codes comprising two Met and two Trp codons [33,34]. (Exact symmetries are exceedingly rare, but near symmetries are common in biology [35]. For example, the left and right hand of the same individual are nearly symmetric: they are mirror images, but not mathematically or physically perfect mirror images.) Code symmetries suggest that the underlying physicochemical and biological mechanisms are identical (or very similar) for the symmetrical entities. For the symmetry between the two codons of all 16, 2-codon sets {NNC, NNU}, the biological cause is known: the 5′GNN3′ anticodons wobble-pair at the 3rd codon position with both NNC and NNU codons in extant biology. Because one anticodon recognizes two codons, the code cannot distinguish between these codons and the encoded message has to be identical for both codons. For other code symmetries (below) the mechanisms are not known, but we conjecture that these symmetries are remnants of no longer observable mechanisms, such as wobble-pairing at the 1st and 2nd codon positions, that operated during the evolution of the genetic code, and thus hold clues as to the evolution of the code itself.

6.2. Conservative and Anti-Conservative Symmetries of the Code

The codon table (Figure 1), a rather arbitrary but ingenious ordering of the 64 codons in 2D-table form, conveniently groups the 16, 4-codon sets differing only at the third codon position into family boxes. These 16 sets {AAN, ACN, …, UUN} correspond one-to-one with the 16, 1 × 1 × 4 tetrahedron faces of the CodonPolytope, a 9D-geometric model determined by (non-arbitrary) intercodon Hamming-distances. The 24 tetrahedron symmetries are exact code symmetries in eight out 16 boxes that encode for a single amino acid (box has one color in Figure 1), and conservative code symmetries in six boxes that encode 2 similar amino acids (the box has two colors that are close on the polar requirement scale of Figure 2). For example, the four GAN-box codons encode the acidic amino acids Asp and Glu, so that all tetrahedron symmetries leave the acidic character of the encoded amino acid invariant. (Substitution of Asp with Glu in a protein is called a conservative mutation; conservative code symmetries leave the physicochemical character of the amino acids invariant.) Arguably only 2 out of 16 boxes lack these conservative symmetries: these boxes contain stop codons (white, no color in Figure 1), which by necessity introduce dissymmetries or asymmetries with codons encoding amino acids.

The other common subdivisions of the codon table also correspond with faces of the polytope. The table itself corresponds with the 4 × 4 × 4 face, the 9-polytope itself, and its left and right halves with two 4 × 2 × 4, 7A-ridges representing the two 32-sets of NYN and NRN codons respectively, with Y = pyrimidine (C or U) and R = purine nucleotide (A or G). The codons of the left table half almost exclusively encode hydrophobic, and those of the right half, predominantly hydrophilic amino acids. (Purple and blue represent hydrophobic amino acids, while orange, yellow and green represent more hydrophilic amino acids in Figure 1; the scale is given in Figure 2). Therefore many of the 2304 symmetries of these faces (their stabilizers are isomorphic with S₂ x_wreath (S₄)₁ × S₂ × (S₄)₃; the S₂ wreath product permutes the 1st and 3rd codon positions, Section 4.4) are conservative or near conservative code symmetries. A few face symmetries are exact code symmetries, but stop codons, or a minority of codons encoding non-similar amino acids in the right table half cause some dissymmetries as well. Most strikingly, the polytope symmetries that exchange the two 7A-ridges (two different 180 rotations generated by two different 2-mirror systems {NAN ↔ NCN, NGN ↔ NUN} and {NAN ↔ NUN, NCN ↔ NGN}), are anti-conservative or near anti-conservative symmetries of the code as they exchange codon assignments between hydrophobic and hydrophilic amino acids for most permuted codons. (An anti-symmetry or black-white, plus-minus, or 0–1 symmetry exchanges parts that are equivalent but of opposite binary value: for example 010 ↔ 101). This hydrophobic ↔ hydrophilic anti-symmetry on the amino acid level corresponds with an anti-symmetry R ↔ Y on the codon level (both 180 rotations above map onto NRN ↔ NYN). Therefore we conjecture that at a very early pre-LUCA stage of the code’s evolution the peptide synthesis machinery distinguished between hydrophobic and hydrophilic amino acids (probably just a few of each kind existed), and at the same time only discriminated between purines and pyrimidines at the middle codon position (the other codon positions do not impact the hydrophobic ↔ hydrophilic anti-symmetry). Recognition of codons by anti-codons through wobble pairing at the middle codon position only, analogous to the wobble pairing at the third position in extant organisms, could have been the biological mechanism underlying the NRN ↔ NYN anti-symmetry. This needs minimally two anti-codons: one with a G and one with a U at the middle position to recognize, respectively, all 32 NYN and 32 NRN codons. The two anti-symmetries, hydrophobic ↔ hydrophilic and R ↔ Y, generate a primitive, initial code capable of controlling to a large extent the hydrophilic / hydrophobic character of synthesized peptides, and thus among others, their 3D-folding and affinity for lipid membranes. This early directed peptide synthesis likely presented a significant selective advantage over a non-directed, random peptide synthesis that probably existed before a genetic code evolved.

6.3. Stronger and Weaker Symmetries of the Code

As mentioned above and continuing that argument, the common subdivisions of the codon table correspond with faces of the polytope. The four columns of the codon table correspond with all four 4 × 1 × 4 congruent 6A-faces, the eight lower and upper halves of these columns with all eight 2 × 1 × 4 congruent 4A-faces, and the 16 family boxes with all 16, 1 × 1 × 4 tetrahedrons as discussed in Section 6.2. Many symmetries of these faces correspond with near conservative or conservative code symmetries, or even with exact code symmetries—all codons encoding the same amino acid are always in the same column/6A-face (except for the six Ser codons, of which four are in the second and two in the fourth column). With exact symmetries seen as stronger symmetries than near-symmetries, or conservative symmetries, then in general, the symmetries of the lower dimensional, smaller polytope faces correspond with stronger code symmetries then those of the higher dimensional, larger faces. (Figure 1 visualizes these differences: the colors of smaller faces are more similar than those of the larger faces; for example, there is a notable difference between the colorings of the four columns, but within each column the colors are rather more similar. Figure 2 indicates how “similar” different colors are; for example, in the first column the Polar Requirements only vary between 4.9 and 5.6.) The smallest faces with the strongest code symmetries—the exact code symmetries, reflect a lack of discrimination between biochemically different molecular entities by the extant protein synthesis machinery. For example, the mirror, or S₂ symmetries of all 16 edges spanned by the two vertices representing the two codons {NNC, NNU} are exact code symmetries due to codon-anticodon wobble pairing at the 3rd codon position. For the small but slightly larger faces, the tetrahedrons, we conjecture that the 24 tetrahedron symmetries, exact symmetries for eight tetrahedrons and conservative symmetries for six tetrahedrons in the extant code, are remnants of exact symmetries of an earlier code based on codon-anticodon Watson-Crick pairing at the first and second codon position while the third position did not matter. At this stage, the code encodes maximally 16 messages, and all tetrahedron symmetries are exact code symmetries (e.g., acidic amino acid is an exact symmetry at this stage). This earlier code evolves to the canonical code when wobble base pairing at the 3rd codon position becomes relevant, and the protein synthesis machinery develops the capacity to distinguish between very similar amino acids, such as Asp and Glu, so that some exact code symmetries evolve to conservative symmetries. By analogy and continuity going back in time, the larger polytope faces with the weaker code symmetries—the near symmetries and conservative symmetries, and the weaker yet—the near conservative symmetries, are remnants of exact symmetries of even earlier codes, going back to the earliest code represented by the two 7A-ridges (Section 6.2).

6.4. Code Symmetries are Not Random

We conjecture above that the symmetries of the code are remnants of its evolution and were not generated by chance in pre-LUCA organisms. To back up this claim a million (10⁶) computer generated random codes composed of the same number of codons per amino acid as the canonical code were screened for exact code symmetries and all numerical data on random codes in this section are results from this simulation. Figure 12 shows codon tables for six random codes with the amino acid color scheme of Figure 2, and visual inspection reveals that the random codes lack most of the symmetries displayed by the canonical code—compare Figure 1 and Figure 12. While the canonical genetic code polytope contains eight tetrahedrons (≈17% of all its 48 tetrahedron faces) displaying exact code symmetries, among the million random code polytopes only 3757 codes contain one, and only two codes contain two such tetrahedrons, and none has more. Thus, random codes with four codons at Hamming 1-distance encoding the same amino acid are rare (about four per 10³ random codes), codes with two such “family boxes” much rarer (about 2 per 10⁶ codes), and more than two extremely rare—so rare that our computer simulations would not stand a chance of generating a random code having eight family boxes like the genetic code (the “trend” suggests only one such code among 10²⁴ random codes). The canonical code polytope possesses 69 edges (≈24% of 288 edges) and 33 triangles (≈18% of 192 triangles) with exact code symmetries, and of these 69 edges 21 are not contained in the eight tetrahedrons displaying exact symmetries, while the same holds for only one triangle. Random codes contain far fewer of these symmetries: none of the random code polytopes possesses more than 28 edges or more than eight triangles (all contained in two tetrahedrons) with exact code symmetries; most frequently random code polytopes contain 11 or 12 such edges (for ≈135,225 per million, or ≈1/6), and no such triangles (≈2/3 has none, and only ≈1/3 has one or more such triangles). Thus stochastic evolution in a pre-LUCA organism will not generate the observed exact symmetry patterns of the genetic code with any practical probability; instead a single, random path most likely generates a code resembling the most frequently simulated codes described above (if the codon assignments of the canonical code are predetermined).

6.5. The CodonPolytope Splitting Model for the Evolution of the Code

If the weaker code symmetries of the larger polytope faces correspond with exact symmetries of more primitive codes, the early evolution of the code in pre-LUCA organisms can be modeled by splitting the CodonPolytope progressively into its smaller faces: 9-polytope → two 7A-ridges → four 6A-faces → eight 4A-faces → 16 tetrahedrons → 32 line segments. At each of these five distinct steps (symbolized by the arrow →) the larger faces split into two, congruent, smaller faces. At each stage of evolution the symmetries of the faces listed, which are the stabilizer groups of the vertex sets spanning them, are exact code symmetries: the vertices of a face and the codons they represent are equivalent under the stabilizer group, these codons encode the same message. The splitting of the CodonPolytope into smaller faces corresponds with the breaking of the symmetry group of the polytope into the smaller stabilizer groups of the faces, and the polytope splitting model is fully compatible with, and illustrates a more mathematically abstract symmetry breaking model for the evolution of the code [24]. Both models progressively partition the codon set in binary fashion; the five steps above split the polytope into smaller faces containing fewer vertices: [64] → 2 × [32] → 4 × [16] → 8 × [8] → 16 × [4] → 32 × [2], for [n] = the set of vertices incident on a face, or the set of codons represented by these vertices. This splitting process generates a binary codon tree (Figure 13).

Non-saltatory, gradual evolution proceeds in small steps, and in a pre-LUCA, primitive RNA world, the emergent protein synthesis apparatus needs to evolve capacities to recognize codons, anticodons, tRNAs and amino acids. We sketch here an outline of a reductionist model that does not address the evolution at the anticodon-tRNA-amino acid levels, which adds another layer of complexity that causes some dissymmeteries of the canonical code, but which are ignored in this section (the assignment process of anticodons, tRNAs and amino acids to the codon blocks of the binary codon tree is discussed in [24]).

The first step splits the CodonPolytope in two 7A-ridges and creates a primitive code distinguishing only between hydrophobic and hydrophilic amino acids and NRN and NYN codons as discussed in Section 6.2.

Figure 12. Codon tables of six random codes. The codes randomly assign the same number of codons to each message as the canonical genetic code. The 64 slots of the codon tables are colored as in Figure 1.

Figure 13. Binary codon tree generated by the five step polytope splitting model. The root node of the tree, labeled 0, represents the 64 codon set, nodes 1 and 2 each represent a 32 codon set, etc., The 32 leave nodes, labeled 31–62, represent 32, 2-codon sets. Each codon set corresponds with the vertices of a polytope face.

The second step splits each 7A ridge into two 6A-faces, each 6A-face corresponds with a column of the codon table. This early code can convey four messages and distinguish between NAN, NCN, NGN, and NUN codons—due to Watson-Crick base pairing at the middle codon position; as well as differentiate between two categories of hydrophic amino acids, the aliphatic and non-aliphatic amino acids—encoded by the codons of the first and second column-6A-face respectively, and between two categories of hydrophylic amino acids, the Arg-like and non-Arg-like amino acids, encoded by the codons of the fourth and third column-6A-faces respectively. The columns of the extant code display remnants of such symmetries; for example 13 of the 16 codons of the first column encode the three aliphatic amino acids, Ile, Leu and Val.

The third step splits the four 6A-faces into eight 4A-faces, corresponding with the upper and lower halves of the four codon table columns. This primitive code comprises eight different messages, and due to wobble base pairing at the 1st codon position (in addition to Watson-Crick pairing at the middle position) minimally eight different anticodons are required to recognize all 64 codons. All 4A-face symmetries are exact code symmetries of this code, and remnants are present in the canonical code. For example, the codons of the upper and lower first-column 4A faces encode, respectively, Leu (6 out of eight codons) or Ile and Val (7 out of eight codons), suggesting that this early code distinguishes between these two sets of aliphatic amino acids: the wobble base paring anti-symmetry Y ↔ R corresponds with the anti-symmetry Leu ↔ Ile/Val on the amino acid level. The second column displays comparable anti-symmetries Ala ↔ Pro and Ser ↔ Thr, which probably also evolved at this stage.

The fourth step splits the eight 4A-faces into the 16 tetrahedrons corresponding with the family boxes. This step corresponds with the imposition of Watson-Crick, rather than wobble pairing at the first codon position, and requires minimally 16 tRNA species for the recognition of all codons and transmission of up to 16 messages. The similarity patterns of the family boxes of the extant codes suggest that this earlier code distinguishes between eight individual amino acids and various subclasses of amino acids, such as the acidic amino acids and subclasses of basic amino acids.

The fifth and last step of the code’s pre-LUCA evolution splits the 16 tetrahedrons into 32 line segments. This step corresponds with the imposition of wobble pairing at the 3rd codon position (in addition to Watson-Crick pairing at the other positions), and requires minimally 32 tRNAs (for non-modified A, C, G and U bases) to recognize all 64 codons. The presence of stop codons in the canonical code is due to the missing of two tRNAs of this minimal set. The code conveys only 21 messages—not 32, because several different tRNA species are charged with the same amino acid. Mitochondrial codes are identical to this primitive code, while the canonical code differs only slightly: one tetrahedron is split into a triangle and a vertex (in Eukaryotes, anticodon IAU, with the rare Inosine base pairs with the three codons encoding Ile and anticodon CAU with the 4th codon encoding Met) and one line segment is broken into two vertices (codon UGA is a stop codon because anticodon UCA of the minimal tRNA set is missing, but the Trp codon UGG is recognized by anticodon CCA, which is not an anticodon of the minimal set) [33,34].

7. Codes Represented by Colorings of the Codon Polytope

7.1. CodonPolytope Colorings as Code Models

As stated in Section 2.1 there are over 1.5 × 10⁸⁴ different code functions that map the 64 codons onto the 21 messages, the C: [64] → [21] surjections, and only one of them is the canonical genetic code. Each of these codes maps each codon to a single message, C: codon-j → message-m, for indices j є [64] and m є [21] (each code is a function); each code maps at least one codon to every one of the 21 messages (an onto mapping or surjection reaches all targets, Appendix A); and in no two codes is this mapping the same for all 64 codons: the map C: codon-j → message-m differs for at least one codon-j for two different codes. Each code is modeled by the CodonPolytope via the mapping f: [64] vertices → [64] codons → [21] messages. Let map f₁: vertex-i → codon-j, for i, j є [64], be fixed for all i and j—that is the same for all codes, then f: vertex-i → message-m is uniquely determined by the code C: codon-j → message-m. Each vertex is labeled with a message and no two codes are represented by the same labeling of the CodonPolytope because at least one vertex is assigned a different message. The mathematical literature with relevance to this section [36] uses colors instead of messages; so let map g: message-k to color-k for k є [21] be fixed for all k—the 21 colors represent one-to-one the 21 messages, then any code C: [64] → [21] corresponds to a specific and unique coloring of the 64 vertices of the polytope with 21 colors via the map f: vertex-i → codon-j → message-m → color-m, for i, j є [64] and m є [21]. Figure 14 illustrates some elementary coloring concepts; Appendix F contains additional background material.

7.2. The Genetic Code Represents a Class of 41,472 Equivalent Codes

In Section 7, the symmetries of the polytope act only on the colors of the vertices, the vertices and the codons they represent are fixed in space—not moved by the symmetries. For example, the NNC ↔ NNU mirror exchanges the vertex colors between the two codons of all 16 codon sets {NNC, NNU}. (In Section 5 the symmetries moved the codons, while the messages were fixed; both uses of the polytope symmetries are equally valid). The NNC ↔ NNU mirror is the only exact symmetry of the canonical genetic code (Section 5) and thus leaves the coloring of the corresponding canonical code polytope invariant (the colors of the 64 vertices are not changed by the actions of this mirror). However, the polytope symmetries that are not exact code symmetries generate different colorings: the colors change for at least two vertices. For example, the NNA ↔ NNG mirror exchanges the “colors” Stop and Trp between the vertices UGA and UGG of the canonical code polytope. The different polytope colorings obtained via the symmetry operations are equivalent—essentially the same, like left and right hands, and form a set of equivalent colorings, a colorings class, which can be represented by a single class member, such as the class of hands by the left hand. All members of the class can be obtained from the single class representative by the actions of the polytope symmetry group. Every coloring belongs to a colorings class (a single member can constitute a class); members of different colorings classes cannot be transformed into each other by the polytope symmetries. Because the polytope colorings correspond with codes, the polytope colorings classes correspond with code classes. A code lacking any exact symmetries (except for the identity) represents a class of 82,944 codes—the maximum size for a code class, because every symmetry operation generates another class member. By the same argument, the genetic code represents a class of 41,472 equivalent codes, and the mitochondrial code a class of 20,736 codes. (The canonical code has two (identity i and mirror μ) exact symmetries, or stabilizers mapping the code onto itself, and the mitochondrial code has four such symmetries (i, μ1, μ2, μ1.μ2) generated by two mirrors; the orbit-stabilizer theorem states: order stabilizer x size orbit = order group; i.e., 2 × 41,472 = 82,944 and 4 × 20,736 = 82,944).

Figure 14. All two-colored tetrahedrons. The 16 ways to color the four vertices of a tetrahedron with two colors, Red and Blue: One tetrahedron with all four vertices Red (4R) and one 4B are shown on the left of the top row, the six tetrahedrons 2R2B fill out the top row and second row, the four 1R3B the third, and the four 3R1B the bottom row. These five sets of colorings are contained in Polya’s colorings classes inventory {4R, 3R1B, 2R2B, 1R3B, 4B}; each class contains equivalent colorings under the symmetry group of the tetrahedron.

7.3. Counting all Classes of Codes Conveying 21 Messages

Polya’s enumeration formula [36] counts the number of colorings classes as a function of the number of colors and the symmetry group of the polytope (Appendix F explains the mathematical theory, and Appendix G contains the cycle index of the polytope symmetry group required for the formula). Polya’s formula for 21 colors counts all classes including those containing fewer than 21 colors that do not represent codes reaching all 21 messages. Therefore, we adapted Polya’s formula to count only classes containing exactly 21 colors: a Polya-21-onto enumeration. (From Polya’s formula for n colors, all p-onto-enumerations for p < n are deducted for n ≤ 21, see Table 3 and Appendix F). The Polya-21-onto formula counts 1.82 × 10⁷⁹ colorings classes of [64] → [21] surjections (see Table 3); representatives of different classes are non-equivalent colorings or codes (under the polytope symmetry group). The ≈1.51 × 10⁸⁴, [64] → [21] codes thus are partitioned into ≈1.82 × 10⁷⁹ code classes with an average class size near the maximum size of 82,944 (the difference is within the rounding error). This shows that almost all codes lack exact symmetries (other than the identity—see Section 7.2), and that the canonical code with two exact symmetries and the mitochondrial code with four exact symmetries have an exceptional symmetrical structure.

Table 3. The number of CodonPolytope colorings classes with up to 21 colors. The first column lists the number of colors, the second the Polya colorings classes, and the third Polya-p-onto count of classes containing exactly the number of colors of the row. Numbers composed of powers of 10, n × 10^m, are listed as “n m”.

**Table 3.** The number of CodonPolytope colorings classes with up to 21 colors. The first column lists the number of colors, the second the Polya colorings classes, and the third Polya-p-onto count of classes containing exactly the number of colors of the row. Numbers composed of powers of 10, n × 10^m, are listed as “n m”.
Number of Colors	Polya Count of Colorings Classes		Polya p-Onto Count of Colorings Classes of Exactly p colors
		Power of 10		Power of 10	% of Polya Count
1	1.0		1.0
2	2.2	14	2.2	14	100
3	4.1	25	4.1	25	100
4	4.1	33	4.1	33	100
5	6.5	39	6.5	39	100
6	7.6	44	7.6	44	100
7	1.4	49	1.5	49	100
8	7.6	52	7.6	52	99.8
9	1.4	56	1.4	56	99.5
10	1.2	59	1.2	59	98.8
11	5.4	61	5.2	61	97.6
12	1.4	64	1.3	64	95.4
13	2.4	66	2.2	66	92.5
14	2.7	68	2.4	68	88
15	2.2	70	1.9	70	83
16	1.4	72	1.1	72	76
17	6.8	73	4.7	73	69
18	2.6	75	1.6	75	62
19	8.4	76	4.4	76	53
20	2.2	78	9.8	77	45
21	5.1	79	1.8	79	35

7.4. Counting All Code Classes that Share the Pattern of the Genetic Code

Polya’s enumeration formula expanded with an explicit list of the colors generates an inventory of colorings classes (Appendix F) [36]; these classes are identified by the number of vertices that are colored with the same color—the colorings pattern (see Figure 14). The colorings pattern of the canonical genetic code is: 1 vertex is “colored” with Met, 1 vertex with Trp; two vertices each with Asp, Asn, Cys, Gln, Glu, His, Lys, Phe, and Tyr; three vertices each with Ile and Stop; four vertices each with Ala, Gly, Pro, Thr, and Val; six vertices each with Arg, Leu, and Ser (the messages are the colors). Polya’s colorings class inventory counts ≈2.79 × 10⁶⁴ colorings classes with the exact colorings pattern of canonical genetic code. (For calculations see Appendix H). Thus, only ≈1.5 of every 10¹⁵ code classes of exactly 21 colors displays this pattern (≈1.5 × 10⁻¹⁵ = ≈2.79 × 10⁶⁴/≈1.82 × 10⁷⁹). A code with this rare pattern is only with vanishing probability generated as a random code of 21 messages. (Our simulations of Section 6.4 used the canonical code pattern as an input to generate only random codes displaying this pattern).

7.5. Colorings Classes under Color Symmetries

In DeBruijn’s generalization of Polya’s enumeration of colorings classes color symmetries exchange colors and thereby reduce the number of colorings classes (Appendix F) [36]. For example, the two Polya colorings {one vertex Met, three vertices Ile} and {one vertex Ile, three vertices Met} are equivalent under a color symmetry exchanging “colors” Met and Ile, and correspond with just one DeBruijn coloring {one vertex one color, three vertices a different color}. S₂₁, the Symmetric group on [21] contains 21! (≈5.11 × 10¹⁹) permutations, and the action of S₂₁ on 21 colors renders them equivalent, although distinguishable. The colorings pattern of the code (Section 7.4 above) induces a set partition of the 64 codons: 1²2⁹3²4⁵6³, for n^m: n = block size, or number of similarly colored codons, and m = number of blocks of size n (for example, 3² stands for the two sets of three codons—Leu and Stop in the canonical code). Since permutations of colors between different blocks of the same size do not alter the colorings pattern, S₂₁ induces M(21; 2, 9, 2, 5, 3) ≈ 4.89 × 10¹⁰ permutations of the colorings pattern (see Appendix A for the multinomial formula) and this renders equivalent as many Polya colorings classes with the same codon set partition, but differing in the colorings of its blocks. These 4.89 × 10¹⁰ different Polya colorings classes “collapse” into just one DeBruin 1²2⁹3²4⁵6³ colorings class. (Here, for example, 3² stands for two blocks of three codons, each block colored differently, but all codons of a block colored identical. Please note the difference with counting set partitions 1²2⁹3²4⁵6³—the sets are not colored differently, but of the same color, only distinguished by size.) Regrettably an enumeration of all DeBruin colorings using 21 colors is not feasible so that the relative frequency of the DeBruin pattern 1²2⁹3²4⁵6³ cannot calculated directly. However because each of the ≈2.79 × 10⁶⁴ DeBruin colorings classes with this canonical code inventory pattern (same as the Polya count for the canonical code inventory, Section 7.3) corresponds with 4.89 × 10¹⁰ Polya colorings classes, there are 1.36 × 10⁷⁵ (≈2.79 × 10⁶⁴ × 4.89 × 10¹⁰) Polya code classes sharing this the DeBruin pattern. Therefore ≈0.75 out of every 10⁴ Polya code classes of [64] → [21] surjections (≈0.75 = ≈1.36 × 10⁷⁵/1.82 × 10⁷⁹—Section 7.3) displays this pattern. These classes are not very rare and a million random [64] → [21] codes are likely to contain on average ≈75 codes that assign the 21 messages in the colorings pattern 1²2⁹3²4⁵6³ of the genetic code, but not with the codon blocks colored as in the code (Section 7.4), and also lacking the characteristic symmetries of the canonical code (Section 6.4).

8. Discussion

The codon table, Figure 2, reveals that similar codons encode similar amino acids and most “obvious” similarities were noted early on [5,6]. The table was even called a periodic table by Jungck [37] because he found that the Polar Requirement of the amino acids correlates with the hydrophylicity of the 3’dimer of their anticodons: a “direct interaction” possibly explaining the pattern of hydrophobic amino acids on the left side of the table, mostly hydrophilic ones on the right side ([37], Figure 5). In Section 6 we map these and other familiar patterns from the codon table onto the polytope, a 9-dimensional geometric object of which the 64 vertices represent the codons in Euclidian space (Section 4.1). Relevant similarity patterns of the codon table map to distinctive faces of the polytope and the Euclidian symmetries of the polytope characterize these patterns as code symmetries (Section 6). For example, the 16 family boxes of the table correspond with 16 tetrahedron faces so that for the eight boxes encoding one amino acid the 24 tetrahedron symmetries are exact code symmetries, while for the six boxes encoding two amino acids they are conservative code symmetries (Section 6). Why go to the trouble of using a geometric object, a rather abstract mathematical model? Why not use the codon table to find and analyze similarity patterns? Indeed many investigators use various rearrangements of the table to find new code patterns that are not obvious from the original layout and then analyze these patterns using distances and symmetries of the table. This use of the codon table is problematic as distances and symmetries of tables are not defined mathematically. There is no “table distance” and codons differing by one point mutation are found not only in the codon’s own family box, but in all four rows and columns of the table. And codons differing by two mutations are found in all other boxes outside the family box. Ignoring the variation at the third base, as is often done, there are 576 equally valid ways to display the layout of the codon table by permuting the order of the bases at the first and second position (576 = 4! × 4!). Certain particular layouts are said to exhibit symmetries, such as a “degenerate mirror symmetry” [38] to name just one example, but tables are not rectangles on the Euclidian plane although our “intuitive eye” sees them as such. (This single “degenerate mirror symmetry” is generated in the polytope by two orthogonal Euclidian mirrors, G ↔ C and A ↔ U, and corresponds to a Euclidian rotation.) The “rectangle” view of the table is compatible with a continuous variation of parameters (such as Polar Requirement) “over” the table that can be displayed as a “continuous smooth surface” in 3-space “with chemical property as altitude” [39]; however neither the table, nor the finite set of parameter values are continuous or smooth so this analysis is problematic, but nicely illustrates the issue at hand.

The Hamming metric of mathematical coding theory is a natural metric for the codon space as one Hamming distance corresponds with one point mutation, the commonly used unit distance between nucleotide sequences. Other metrics define different spaces; for example, Dragovich and Dragovich [40] use a p-adic, ultrametric norm; the four nucleotides are at one 5-adic and four codons differing only in the 3rd position are at 1/25 5-adic distance from each other. shCherbak [41] assigns codons integer nucleon numbers of their encoded amino acids and develops a digital arithmetic code. Jungck [42] reviews many of the “genetic code as mathematical code” models; the discussion below focuses on those most related to our approach.

The CodonDistanceMatrix (Figure 4) and the CodonGraph (Figure 5 and Figure 10) display the intercodon Hamming distances of the (normed, Hamming metric) codon space, and their symmetries are described by permutation groups (Section 5), but they lack the mirror reflection and axial rotation symmetries of Euclidian space. (In Euclidian space an inner product defines the required angles and distances for these symmetries). In a non-Euclidian, graph topological approach, Tlusty [43] embeds a codon graph with 48 vertices (synonymous codons ending in C or U are represented by the same vertex) and 192 edges on a 2-dimensional surface of genus 25 (25 holes are needed to avoid edges from crossing) and chromatic number 20 (20 colors are required to color all neighboring quadrilaterals differently); this coloring number (20) is the upper limit for encoded amino acids by this configuration and equals the number of amino acids of the genetic code. A similar embedding of a 64 vertex, 288 edges graph, defined like the CodonGraph, has genus 41 and chromatic number 25, a topology encoding up to 25 amino acids. (The CodonGraph, shown in circular and array embedding in Figure 5 and Figure 10, can encode up to 64 messages). Chechetkin [44] uses a De Bruijn graph with 16 vertices representing the 16, 2-mers of the four nucleotides, and 64 directed edges representing the codons overlapping with both vertices (vertex AA is joined by edge AAC to vertex AC) to study the translational stability of the code. Tlusty [43] noticed that the 64 vertex, 288 edge CodonGraph is “natural” to be used for this purpose as is discussed further below.

The CodonPolytope (Section 4), a 9-dimensional geometric object in Euclidian space preserves the Hamming metric of the codon space: the intercodon Hamming 1-, 2- and 3-distances correspond one-to-one to the three particular Euclidian distances between the 64 vertices of the polytope representing the codons; in one realization of the polytope these distances are 2√2, 4, and √6, respectively (Section 4.1 and Section 4.2). The Euclidian reflection symmetry group of the polytope, the permutation symmetry group of the graph, and the largest permutation group that preserves the Hamming metric of the codon space, are all three isomorphic to S₃ x_wreath (S₄)₁ × (S₄)₂ × (S₄)₃ (Notation: the index-i for i = 1, 2, 3, in (S₄)_i corresponds with the codon position acted on by the S₄ group); S₄ permutes {A,C,GU}, S₃ the three codon positions (Section 4.3 and Section 5). This group contains all 82,944 symmetries of the 64 codon set that preserve the intercodon Hamming distances (the distance between any two codons before and after the permutation is the same). The group induces permutations of the codon set and rearrangements of the codon table; for example, the two S₄ acting at the first two codon positions induce all 576 codon table layouts mentioned above.

To our knowledge, apart from the CodonPolytope, no published geometric model of the code preserves the Hamming metric. The often used 6-cube, 6-bit codon model ([12,13,14,15,16,17] and many references herein) does not preserve intercodon Hamming distances as discussed in the introduction. Moreover the symmetry group of the 6-cube of order 46,080 is smaller than the polytope group, but is not a subgroup of the polytope group and therefore contains 6-cube symmetries that do not preserve intercodon Hamming distances: only the 384 symmetries of the 6-cube subgroup S₃ x_wreath (S₂ × S₂)₁ × (S₂ × S₂)₂ × (S₂ × S₂)₃ preserve these distances (Section 4.3); the (S₂ × S₂) groups are isomorphic to the Klein-4 group, see further below. In general hypercube models of nucleotide sequences such as those used by Eigen ([45], pp. 354–387) do not preserve the intercodon Hamming distances (as they do not contain triangles or tetrahedrons, Section 2.5). Nonetheless the 6-cubes are frequently used for analysis of code patterns: Jiménez-Montaño et al. [17] hold that the cube structure explains amino acid substitution patterns, and according to Karasev and Stefanov [18] the 6-cube’s topology encodes a 4-amino acid-arc helical protein topology—the “topological nature of the code”. Several investigators [12,15,17,46] derive genetic Gray codes based on the cube’s Hamming distances. The 3D “Genetic Hotels” [16,19,47,48] are projections of the 6-cube onto a “3-cube” in R³ space, a 3D-version of the codon table with {C,U,A,G} mapped to {0,1,2,3} and the 1st, 2nd and 3rd codon positions plotted on the x, y and z axes respectively, so CCC corresponds with (0,0,0) and GGG with (3,3,3). The hotel “cube” resembles the CodonArray graph, Figure 10, but the hotel has only three edges per row or column, while the graph has six edges per row and is not a geometric object. In the hotel, the intercodon Hamming 1-distances vary from one to two to three cube edges; the hotel thus distorts this metric even more than the 6-cube. Moreover, the hotel 3-cube is not Euclidian, as the 0, 1, 2, and 3 coordinates are projections of the values 0, 1, α, and 1 + α of the Galois 4-Field: the distance between 1 and α equals 1 + α (not 1 as the cube suggests), and between 1 and 1 + α actually equals α (not 2). The hotel cube can be manipulated with Galois 4-Field algebra (four additions, three multiplications), but does not possess Euclidian symmetries. Different projections onto the hotel result in different 3D-code geometries; for example (C,U,A,G) produces hotel-cube-edges for amino acids encoded by just two codons [16], but (G,U,A,C) does not [48]. Other three-dimensional geometries such as a simple tetrahedral construct with 20 lattice points representing 64 codons [49] also do not preserve the Hamming metric. In fact any geometry preserving this metric in Euclidian space has to be isomorphic to the CodonPolytope (by a mathematical theorem, Section 4.1), a simple 9-polytope, and therefore no such object could exist in a Euclidian space of fewer than nine dimensions. This polytope thus provides a unique geometry for the identification of code symmetries by well-defined Euclidian symmetry transformations such as mirror reflections and rotations. The polytope has 82,944 symmetries, so one is bound to find a few interesting non-obvious code patterns and intriguing symmetry subgroups, but their biological significance might not be obvious either.

Jestin and Soulé [50] identify three “base substitution symmetries” of the code; in our vocabulary these symmetries correspond with mirror symmetries of the codon polytope. As reviewed in [14] the “Rumer transformations”, first reported by Rumer in Russian 1968, have been extensively analyzed, but their biological significance has not been identified. Of the 16 family boxes, eight each encode a single amino acid (the M1 set of boxes), and the other eight (the M2 set) encode two or three messages. The single “degenerate mirror symmetry” of the UCGA × UCGA layout of the codon table mentioned above [38] or two “base substitution symmetries” G ↔ C and A ↔ U at the first codon position [51] map the two sets of boxes onto themselves. The “Rumer transformations” exchange A ↔ C and G ↔ U at all codon positions and thereby exchange the 8-sets, M1 ↔ M2, as reviewed in [14,50]. Danckwerts and Neubert [52] define three operators α, β, γ acting on nucleotide characters; α: Purine ↔ Pyrimidine, β: Weak ↔ Strong, or 2 H-bonds ↔ 3 H-bonds, and γ: Amino ↔ Keto; or α: (A ↔ C, G ↔ U), β: (A ↔ U, G ↔ C) and γ: (A ↔ G, C ↔ U). These plus an identity operator make up an operator group isomorphic to the Klein Four group that permutes the four nucleotides. The Rumer transformation corresponds with α acting on all three codon positions [52], or with γ acting on the first, and α on the second and third codon positions as was found later by Jestin and Soulé [50]. Jiménez-Montaño [14] showed that a CGUA × CGUA table displays a “yin yang” pattern for the two 8-box sets M1 and M2, various “quadrant” patterns for the two nucleotide characteristics (R/Y and S/W), and Gray codes based on the 2-bit nucleotide representations. In a group theoretic approach Findley et al. [53] identify the four nucleotides with the four group elements of the Klein-4 or the Z4 group (cyclic group of order 4) and generate the 64 codons as product group K × K × K = K (three elements of K multiplied produce an element of K). Thus each codon identifies with an element of K and thereby with one of the nucleotides: the codons are partitioned in four blocks of 16 codons. The Klein-4 group induces a unique codon partition with degeneracies equivalent to those of the genetic code; the Z4 group induces six different partitions with different degeneracy patterns.

Historically various geometric models were used to analyze these patterns and symmetries. Danckwerts and Neubert [52] illustrate the Klein-4 group (=K) with a square having the four nucleotides as vertices and the group elements (α, β and γ) as edges and diagonals, while Jiménez-Montaño [14] uses a rectangle in an identical way; Bertman and Jungck [54] showed a tesseract or 4-cube representation of K × K having the 16 dinucleotides as vertices, and two group elements (α and β) as edges so that all eight vertices of the set M1 (dimers of 4× degenerate codons) lie in three connected planes (2D-square faces, in our parlance). The Klein-4 group is isomorphic to the bitwise addition group for {00, 01, 10, 11} [14,16]—the very definition of a Hamming square, as well as to the rectangle symmetry group, and therefore investigators often use the rectangle and square models simultaneously. Remarkably the isomorphism with the Euclidian rectangle mirror symmetry group (identity, two mirrors bisecting the opposite sides, and one 180 degree rotation) was never used explicitly. The Klein-4 group also is isomorphic to the rotation symmetry subgroup of order 4 (identity, 180 degree rotations on three orthogonal axes) of A3—the tetrahedron reflection symmetry group; A3 is isomorphic to S₄, and Klein-4 is isomorphic to S₂ × S₂, a small subgroup of S₄. These isomorphisms show that the symmetries and similarity patterns discussed above can all be expressed as Euclidian symmetries of the tetrahedron and CodonPolytope. The other geometries have drawbacks because the 24 ways to label the four vertices of a square or rectangle with {A,C,G,U} are not equivalent. The non-equivalent ways of labeling correspond with different neighborhoods for each label. Depending on the labeling of the vertices, different nucleotides are non-adjacent (diagonally opposite vertices are separated by two edges, not one), or if on a rectangle, adjacent via long or short edges. Therefore the edge or Euclidian distance between the vertices in these models cannot coincide with the “one point mutation” distance between the four nucleotides, and this is also why n-cube models cannot preserve the intercodon Hamming distances. In contrast, all ways of labeling the regular tetrahedron are equivalent: all four vertices are at 1-edge and at identical Euclidian distance in correspondence with the Hamming 1-distance between the nucleotides. Moreover the tetrahedron A3 reflection symmetry group contains subgroups isomorphic to the rectangle and square symmetry groups, and the polytope as product of three tetrahedrons contains all products of these symmetries, such as K × K × K and K × K mentioned above, in its direct product symmetry subgroup A3 × A3 × A3, isomorphic to (S₄)₁ × (S₄)₂ × (S₄)₃.

The CodonPolytope and its faces display many code symmetries (Section 6): exact symmetries permuting synonymous codons, conservative symmetries permuting codons encoding similar amino acids, anti-symmetries that exchange codons encoding amino acids with opposite characteristics (such as hydrophobic and hydrophilic) and near (not perfect) symmetries of all three kinds. The larger polytope faces display weaker, less perfect code symmetries than the smaller faces, which display stronger, more perfect and exact symmetries. This hierarchy of faces and symmetries suggests that the stepwise splitting of the polytope into its smaller faces models an early evolution of the code that generates the similarity patterns of the extant codes (Section 6.5). This model is fully compatible with a more abstract symmetry breaking model [24]. Both models partition the 64-codon set along a binary tree in five steps to 32, 2-codon blocks; at each step the codon blocks correspond with the polytope faces generated by the splitting process. Increasing codon-anticodon base pairing stringencies from none to wobble to Watson-Crick, initially at the middle codon position, subsequently at the first, and lastly at the third position (but only to wobble at the third position) as in the sequential “2-1-3” model [55], partitions the codons in exactly this manner. At each stage each codon block (polytope face) encodes a class of similar amino acids; the members of this class are not differentiated from each other by the cellular machinery so that the face symmetries correspond with exact code symmetries. Only during the final fifth step is the class size reduced to one specific amino acid for all codon blocks. This process generates the extant mitochondrial codes and nearly the canonical code. Early codes are ambiguous as each codon block encodes similar amino acids and these similarity patterns are (near) conservative symmetries in the extant codes. For example, almost all codons represented by a polytope 6A-face (corresponding with the left column of the codon table) encode aliphatic hydrophobic amino acids, a remnant of an early code that neither distinguishes between the 16 NUN codons of the left column, nor between these very similar amino acids. The polytope model makes no particular assumptions about the presence or absence of particular amino acids during its evolution, but most likely amino acid repertoires increased over time [56]. If at the four 6A-faces stage only Val is present, and the other aliphatic amino acids, Ile and Leu have not yet been generated, then all codons of the 6A-face block encode Val and only at the next, eight 4A-face stage are the codons of one of the 4A-blocks reassigned to Leu, while the codons of the other block encode Val and Ile. Thus, the polytope model is compatible with Higgs’s “four column model” [57] and Wong’s and Di Giulio’s coevolutionary theory [58,59] that assign amino acids sequentially to specific codon blocks. Such assignments also depend on the evolving specificities of primitive RNA-based aminoacyl-tRNA synthetases (aaRSs) for blocks of tRNAs and classes of amino acids [60]. For example, the early aaRS for Val evolves to three aaRSs differentiating between the three aliphatic amino acids and the seven tRNAs complementary to different codon blocks of the extant code [24].

Delarue [61] found an “asymmetric pattern” in the AGCU × CUGA layout of the codon table that depends on whether the encoded amino acid is recognized by a Class I aaRS or a Class II aaRS. Rodin and Rodin [62] rearrange the table differently with “complementary” codons “face to face” to show a “latent mirror symmetry,” while Jestin and Soulé [50] describe this pattern by six “base substitution symmetries”. The pattern maps to distinct polytope faces and “recapitulates” the progression of splits of our evolution model: the two NUN and NCN 6A faces (table columns) are Class I and Class II respectively, in correspondence with a NUN ↔ NCN = Class I ↔ Class II anti-symmetry mirror in our nomenclature. The two NRN columns are split into upper and lower 4A faces, in correspondence with a NYN ↔ NRN = Class I ↔ Class II anti-symmetry mirror of the 6A faces, etc., which leads to a binary partition of the codon set [61] and decision tree [14] much like our polytope splitting model (Section 6.5).

The clustering of same and similar amino acids on the faces of the polytope (with vertices representing encoded amino acids) and the related exact and conservative code symmetries (Section 6, and discussed above) confers on the code a degree of robustness to mutations and reading errors because single errors correspond with polytope symmetries (mirror reflections of the affected codon). As the genetic code displays many near-symmetries this robustness seems suboptimal, and indeed codes less prone to errors have been found, as reviewed by Santos and Monteaguado [63]. The error-sensitivity of the code defined as the average variation in Polar Requirement of the amino acids encoded caused by all single point mutations affecting all codons [63], can be computed as the average edge weight of the CodonPolytope/Graph with edge weights reflecting the difference in Polar Requirement between the neighboring amino acid vertices on polytope (or graph); Tlusty [43] considered the graph a natural way to study the impact of mutations, and Buhrman et al. [64] explicitly constructed the graph for their computations. Polytope/graph faces with exact code symmetries contribute nil to the total edge weight; those with conservative symmetries less than those with near conservative or anti-symmetries. On the one hand symmetry breaking [21,22,23,24,65], code trees [14,61] and polytope splitting generate symmetric codes with error robustness, but on the other hand selection for codes with low error loads during the pre-LUCA evolution of early codes, the error minimization hypothesis [66], should generate codes with many symmetries.

Several group theoretical models [21,22,23], reviewed in [65], evolve the code from an initial group with a 64-dimensional irreducible representation (irrep) under which all 64 codons are equivalent, via a series of symmetry breaking steps, into subgroups with smaller dimensional irreps, corresponding exactly with the codon degeneracies (the block partition 1²2⁹3²4⁵6³ of the codon set, Section 7). Antoneli et al. [21] claim to have screened all algebraic models within this approach, whether based on Lie groups/Lie algebras, on Lie superalgebras or on finite groups ([21] reviews all earlier work in this area). They identified several Symplectic groups, but foremost Sp(6) and its supersymmetric version as “unique solution”. The Sp(6) model evolves the canonical code from the initially non-coding 64 codons in at most four steps (Figure 5 in [21]). The first step generates six subgroups comprised of 20, 16, 10, 4 and two codons, encoding respectively Gly, Ala, Ser, Val, Asp, and His; in the second step the 20 Gly codons split into eight Gly, six Cys, and six Ile codons (and all other groups other than the two His codons split up as well); and in a third step the six Ile codons split in three Ile and three Stop codons, and most other codon blocks split as well. This splitting scheme generates the codon partition of the canonical code per force—some subgroups are artificially “frozen” (partial symmetry breaking) as otherwise blocks of synonymous codons are split into smaller sets. The similarity patterns of the early codes do not seem to match those of the codon table at all (for example, the three Ile and three Stop codons do not form one block of six related codons), and the fixation of the two His codons in the earliest code seems particular. Only three finite Symplectic groups [23] of orders 103,608; 2,903,040; and 4,245,696 evolve the code under partial symmetry breaking; these groups do not break in a predetermined order and, thus, generate a variety of early codes. Bashford et al. [22,65] find that the Lie superalgebra A(5,0) ≈ sl(6.1) can evolve the anticodon genetic code (anticodon as opposed to amino acid assignments to codon blocks) through partial symmetry breaking in five to six steps in three different ways, one of which resembles the binary tree models mentioned above ([14,24,61] and the polytope model). In a different approach, Sciarino et al. [20,67] assign the four nucleotides to the irreps of the quantum group Uq(su(2)⊕ su(2)) in the limit q → 0 (the crystal basis), obtain the codons as tensor products of the nucleotides, and their amino acid assignments as eigenvalues of a codon reading operator; different genetic codes correspond with different operators. A more recent application of this Crystal Basis Model [68] determines codon-anticodon pairing based on the “minimum principle” of the mitochondrial code: anticodon wobble base U is identified for family boxes of four synonymous codons, and G and U for boxes with two pairs of synonymous codons. This quantum group does not evolve codes, but computes similar wobble bases for early codes such as the “Archetypal” code (15 family boxes encoding a single amino acid, one box encoding Tyr and Stop, each by two codons) [69], which closely resembles the 16 tetrahedron stage of the polytope splitting model. These group theoretical models are mathematically ambitious, but none evolves ab inito with complete symmetry breaking the genetic code from a primordial non-differentiated codon set (no such group was found). The riddle as to how the code itself evolved in pre-LUCA organisms is thus alive and well.

The canonical genetic code is unique, but how unique? Taking the 64 triplet codons as a given, 64! ≈1.3 × 10⁸⁹ different codes are possible; these codes assign up to 64 messages to the 64 codons. Assuming the 21 messages of the canonical code, the literature sometimes uses 21⁶⁴ ≈ 4.2 × 10⁸⁴ as “first approximation,” but there are 1.5 × 10⁸⁴ (≈36% of 21⁶⁴) codes that convey exactly 21 messages, or [64] → [21] surjections [24]. If one further assumes the number of codons assigned to each message by the canonical code as fixed, i.e., one codon to Met, six codons to Ser, etc, then the number of codes is given by the multinomial formula M(64, 1²2⁹3²4⁵6³) ≈ 2.3 × 10⁶⁹ (Appendix A. An often quoted formula from ([70], p. 96) is incorrect.) None of these calculations takes the 82,944 symmetries of the polytope into account. Polya’s formula enumerates colorings classes of geometric objects—in each class all colorings are equivalent (essentially the same) under the symmetry group of the object [36]. We adapted Polya’s enumeration to count only colorings using exactly 21 colors (and not fewer), the colorings then correspond with codes. When applied to the CodonPolytope with 20 amino acids and one stop signal as 21 colors the canonical code represents a class of 41,472 equivalent codes, and the mitochondrial code a class of 20,736 codes (Section 7.2). The ≈1.5 × 10⁸⁴, [64] → [21] surjections are partitioned into ≈1.8 × 10⁷⁹ code classes with an average class size of ≈82,944 (within rounding), the maximum class size as virtually all codes, unlike the canonical and mitochondrial codes, lack exact symmetries. (Section 7.3). The ≈2.3 × 10⁶⁹ codes that assign the same number of codons to same message as the canonical code are partitioned into ≈ 2.8 × 10⁶⁴ classes of size ≈82,944 (Section 7.4); These spaces of code classes are too vast to find even a single representative of any of the classes of the few extant codes among billions of randomly generated codes; in other words, there is no chance of generating codes like the genetic code by chance.

Acknowledgments

The author thanks his spouse Toni Claudio for fruitful discussions and critical proofreading of the manuscript, and the three anonymous reviewers for their constructive comments and references to relevant literature.

Conflicts of Interest

The author declares no conflict of interest.

Appendix A. Some Discrete Mathematics, Notation and a Few Combinatorial Formulas

Let [n] stand for the finite n-set of positive integers, {1, 2, 3, …, n−2, n−1, n}, then [n] is an index set for any finite n-set of objects; for example, {1, 2, 3, 4} or [4] is an index set for the set of four letters, {A, C, G, U}—each letter is indexed by the corresponding number: A₁, C₂, G₃, U₄. Because of this one-to-one correspondence between the index set and object set, mathematical formulas that are valid for the general index set are valid for the specific object set. We refer to Mazur’s book for the notation and the formulas used in this appendix [25].

A mapping, map, or function on [n] is a relation of [n], the domain, with a set [m], the range or target that relates every element of [n] with one (and only one) element of [m]; we use the notation, R: [n] → [m]: for all n є [n] there exists one and only one m є [m] for which the relation R, nRm, or R: n → m is valid. Other common notations for nRm are R(n) = m, and (n, m). The genetic code is a function C: [64] → [21] as every element of the 64-codon set encodes just one element of the 21-message set—the 20 amino acids and a termination signal. The inverse relation between the 21-message set and the 64-codon set is not a mapping as, for example, Arg is encoded by six codons and not only by one (the unique relation: Arg → X is not defined, as X can be any of six codons). Thus, the genetic code is not a reversible mapping; it is an irreversible map, which indicates that information cannot be easily transmitted backwards from amino acid to codon and indeed the central dogma as formulated by Francis Crick states that information flows from DNA to RNA to protein, but not backwards. (The mapping DNA → RNA is reversible mathematically, and biologically by reverse transcriptase, which was discovered after Crick formulated the central dogma—one ignores fundamental mathematics at one’s peril.) Mathematical codes, such as binary computer codes designed by humans to transmit information are reversible codes [n] ↔ [m], so that both coding and decoding are functions and information is easily transmitted both ways.

A map of [n] onto [m], or surjection [n] → [m], is a map [n] → [m] that reaches all m є [m]. So for all m є [m] there is at least one n є [n] for which the map n → m is defined; every image m є [m] has at least one pre-image n є [n]. Let N and M be the number of elements in [n] and [m] respectively, then N ≥ M as every n є [n] reaches only one m є [m], but a m є [m] can be reached by more than one n є [n]. The genetic code is an onto-mapping [64] → [21]. All messages are encoded by at least one codon. As opposed to a surjection, an injection [n] → [m], a map of [n] into [m], may not reach all m є [m]; an m є [m] does not have a pre-image n є [n] if the function maps none of the n є [n] to this m є [m], and thus N ≤ M.

Permutations are mappings of an n-set onto itself: [n] → [n], and of course N = N. Permutations are reversible mappings or bijections: [n] ↔ [m]; n → m, every pre-image n є [n] has only one image m є [m], and n ← m, every image m є [m] one pre-image n є [n], and thus N = M.

The number of permutations of n objects or [n] is given by n-factorial or n! = n × (n–1) × … × 2 × 1. For example, the letters of {A, C, G, U}, indexed by [4], can be rearranged as an ordered 4-tuple (1, 2, 3, 4) in 24 ways: four choices for the first position, three for the second (as no letter can be used twice), two for the third and one for the fourth position = 4 × 3 × 2 × 1 = 4! = 24.

The number of ways to choose k objects from n objects equals the number of combinations, or the binomial coefficient, C(n,k) = n!/(k! × (n–k)!). For example, the number of ways to select two vertices from the four vertices of a tetrahedron equals C(4,2) = 4!/(2! × (4−2)!) = 4!/(2! × 2!) = 6; each 2-vertex set corresponds with one of the six edges of the tetrahedron. The binomial coefficient counts the number of ways n objects can be distributed over two boxes: k objects in the box labeled “chosen” and (n–k) objects in the box labeled “rejects”—two boxes with different labels, but any order of the objects in the boxes is valid—the k-objects can be ordered in k! ways, and the (n–k) objects in (n–k)! ways.

The multinomial coefficient counts the number of ways a set of objects can be distributed over different boxes, such as the set of 64 codons over 21 boxes labeled with the 21 messages of the code—a different label for each box. Let the sum of positive integers k, l, m, … , z, equal N, the size of [n], then the multinomial coefficient equals M(N; k, l, m, …, z) = N!/(k! × l! × m! × … × z!); the first box contains k objects, the second l objects, etc. For example, let [c] stand for a set of codons encoding the same amino acids in the canonical genetic code, i.e., [1] for the codon set encoding Met, and [6] for the set encoding Arg, then the genetic code can be represented by the sets 2 × [1] + 9 × [2] + 2 × [3] + 5 × [4] + 3 × [6], or 1²2⁹3²4⁵6³ (21 sets), then the number of ways to distribute the [64] codon set over the 21 boxes labeled with the messages equals M(64, 1²2⁹3²4⁵6³) = 64!/(1!² × 2!⁹ × 3!² × 4!⁵ × 6!³) ≈ 2.316 × 10⁶⁹. (Biologists often quote [70] but his formula (p. 96) and result are mistaken: because he does not count the three stop codons, his formula has one factor 3! in the denominator, but then his nominator should read 61!—not 64!, and his result should be 5.56 × 10⁶⁴—not 1.40 × 10⁷⁰ as in his text).

When the boxes are not labeled, but n-sets distinguished only by their size, then p n-sets of the same size can be arranged in p! indistinguishable ways. For example, the genetic code has nine sets of 2-size, and all 9! orderings of these boxes are indistinguishable. The number of ways that the 64-codon set can be distributed over the 21 sets of the genetic code’s set partition 1²2⁹3²4⁵6³ is thus given by: M(64, 1²2⁹3²4⁵6³)/(2! × 9! × 2! × 5! × 3!)] ≈ 2.16 × 10⁶⁰; the factor (2! × 9! × 2! × 5! × 3!) ≈ 1.045 × 10⁹ corresponds with the number of ways the genetic code’s sets can be permuted. The formula counts the number of set partitions of [64] with the size of the subsets equal to 1²2⁹3²4⁵6³ (21 sets). The genetic code’s set partition is quite unique: fewer than 1 in 10,000 partitions of [64] into 21 blocks are comprised of similar sized blocks. (There are S(64,21) ≈ 2.96 × 10⁶⁴ partitions of [64] in 21 sets—a Stirling number, see below; 2.16 × 10⁶⁰/2.96 × 10⁶⁴ ≈ 0.75 × 10⁻⁴).

Neither the multinomial coefficient, nor the set partitions do enumerate all possible ways to map 64 codons onto 21 messages, C: [64] → [21]. The computation of the number of surjections, C: [64] → [21] has two parts: First, the 64-codon-set is divided up into 21 non-overlapping, non-empty subsets (blocks), like dividing 64 cards into 21 stacks—this is a set partition. Second, the 21 blocks of the set partition are mapped onto 21 messages: [21] → [21], which can be done in 21! ways, the number of permutations of [21]; each codon block is assigned a different message, so all 21 messages are reached. The number of partitions of an n-set into k blocks is given by the Stirling number of the second kind, S(n,k), an elementary formula but long to derive (Mazur 2010). Thus, the number of onto coding functions: [64] → [21] equals S(64,21) × 21! =

\sum_{j = 0}^{21} C (21, j) x {(- 1)}^{j} x {(21 - j)}^{64}

≈ 1.51011 × 10⁸⁴—an astronomically large number (in this formula C(21,j) is a binomial coefficient.) Nonetheless, these coding functions are just a subset of ≈36% of all 21⁶⁴ ≈ 4.18827 × 10⁸⁴ mappings of the 64 codons to the 21 messages, most of which reach only 20 or fewer targets (i.e., most of these 21⁶⁴ functions are injections not surjections) [24].

Appendix B. Permutations, Groups and Group Isomorphisms

There are n! permutations of the n-set: [n] → [n], (Appendix A). A permutation corresponds with a reordering of the n-numbers of an ordered n-tuple (1, 2, …, n). For example, the 3! = 6 permutations of [3] are: the identity permutation (1,2,3) that keeps the original order, three inversions or transpositions (1,3,2), (2,1,3), (3,2,1) that reorder only two numbers, and two permutations (2,3,1) and (3,1,2) that reorder all three numbers. The inversion (1,3,2) is short for the mapping: 1 → 1, 2 → 3, and 3 → 2, corresponding with the exchange 2 ↔ 3, while 1 is fixed, not moved.

As a permutation maps the n-set onto itself, one permutation π1 can be followed by another π2 as the image of π1 equals the pre-image of π2. This composition or product of the two permutations: π1∙π2, maps the n-set onto itself and equals a third permutation π3 of [n]. For example, the composition of the two inversions (1,3,2)∙(3,2,1) reads 1 → 1→ 3, 2 → 3 → 1, and 3 → 2 → 2 and thus equals (2,3,1), a reordering of all three numbers. A fundamental theorem states that all permutations can be composed of inversions. For example the identity equals twice the same inversion: i = (1,2,3) = (1,3,2)∙(1,3,2).

The Symmetric group on n objects, or S_n, is made up by the set of all n! permutations of [n] in combination with the composition of these permutations. The size of S_n equals its order. For example, S₃, the Symmetric group on three objects of order six is made up by the six permutations of [3] and their composition. The Symmetric group is a mathematical group because it is closed (two permutations make another permutation: π1∙π2 = π3 є S_n), composition is associative (the order of multiplication of more than two permutations does not matter: (π1∙π2)∙π3= π1∙(π2∙π3)), it contains an identity (i), and every permutation π is invertible by its inverse permutation π⁻¹ (π∙π⁻¹= i).

Mathematical groups are fundamental structures describing, among others, symmetries, which are operations on a set that leave some aspect of the set the same. For example, the symmetries of an equilateral triangle map the triangle on itself: the position of the triangle is the same before and after the symmetry operation. In particular the set of three vertices is mapped onto itself: [3] → [3]. An equilateral triangle (Figure 8) has three mirror planes—they are incident on one vertex and bisect orthogonally the opposite edge, and reflections in these planes fix the vertex in the plane, but exchange the two other vertices. In Figure 8 the three vertices are labeled (1,2,3) counterclockwise and the three mirrors, μ1, μ2, μ3; reflections in these mirrors move the vertices: (1,3,2), (3,2,1), (2,1,3), in one-to-one correspondence with the three inversion permutations of S₃. In addition, the three mirrors intersect in the geometric center of the triangle and their line of intersection forms a rotation axis for 0 = 360, 120, and 240 degree counterclockwise rotations: σ₀, σ₁₂₀, σ₂₄₀. These symmetries of the triangle relabel the vertices: (1,2,3), (3,1,2), and (2,3,1) respectively, in one-to-one correspondence with respectively the identity and the two reordering permutations of S₃. Each rotation can be generated by two mirror reflections: the angle between the mirrors is 60 degrees and reflection in one mirror followed by reflection in the next counterclockwise mirror generates a rotation of 120 degrees (e.g., μ1·μ3 = σ₁₂₀); a second reflection in the previous counterclockwise mirror generates a rotation of −120 = + 240 degrees (e.g., μ1·μ2 = σ₂₄₀). The zero degree rotation or identity is obtained by reflecting twice in the same mirror. These six symmetries of the equilateral triangle also form a mathematical group (the group requirements listed above are met). The symmetry group of the equilateral triangle is known as D3 (dihedral 3-group); D3 is a reflection group as all its symmetries can be generated by mirror reflections, and D3 is a point group as its geometric center is fixed by all symmetries (the center is unique and always mapped to itself).

D3 and S₃ are isomorphic: they correspond with the same abstract group of six elements and rules of composition. As shown above every symmetry of D3 induces a permutation of the vertex labels (1,2,3) that is an element of S₃, and the six symmetries of D3 correspond one-to-one with the six permutations of S₃ (both groups have the same order). In addition, the composition of two symmetries (such as two reflections) corresponds with the composition of the corresponding permutations (two involutions). The reversible function (bijection) Φ mapping the symmetries to permutations with preservation of composition of the group elements is called an isomorphism; that is let Φ(μ1) = (1,3,2) = π1 and Φ(μ2) = (3,2,1) = π2; then Φ(μ1∙μ2) = Φ(μ1)∙Φ(μ2) = π1∙π2 = (1,3,2)∙(3,2,1) = (2,3,1) = Φ(σ₂₄₀) = Φ(μ1∙μ2); and so in general for any two symmetries s1 and s2: Φ(s1∙s2) = Φ(s1)∙Φ(s2).

The six permutations of the three codon positions, represented by an ordered 3-tuple, (1,2,3) correspond with those of S₃, but equivalently, S₃ acts on the three codon positions (1,2,3) as a symmetry group and induces six permutations of the codon positions—group actions on the codon positions, a common way to describe symmetries. D3 is generated by three 2-dimensional plane mirrors and a group isomorphic to D3 is generated by three 8-dimensional hyperplane mirrors and permutes three 3-dimensional subspaces in 9-space as described in Section 4.3. This group is a symmetry group of the CodonPolytope and induces the six permutations of the three codon positions by relabeling the 64 vertices of the CodonPolytope, analogously to the relabeling of the three vertices of an equilateral triangle by D3, and with a one-to-one correspondence to the actions of S₃ on the three codon positions—these groups are isomorphic.

The Symmetric group on four objects, S₄, of order 4! (=24), acting on the four letters of the alphabet of the genetic code, in lexicographical order—(A,C,G,U), permutes their order. For example, the inversion (2,1,3,4) induces the reordering (C,A,G,U) or the exchange A ↔ C, while fixing G and U. S₄ is isomorphic to the symmetry groups of the K4-graph and the tetrahedron (Appendix C): the 24 symmetries of the graph and the tetrahedron leave them invariant but permute the vertex labels and thereby induce the 24 permutations of S₄. S₄ acts on the codon set by permuting these four letters at a particular codon position; for example, acting on the letters at the 3rd codon position, the exchange A ↔ C induces the exchange of 32 codons NNA ↔ NNC (short for AAA ↔ AAC, ACA ↔ ACC, etc.), while fixing the 16 NNG and 16 NNU codons. The permutations of the codon set: [64] → [64], induced by such actions of S₄ are symmetries of the codon set: they fix the set set-wise, the set itself is invariant (indeed all 64! permutations of [64] are symmetries of the codon set). A copy of S₄ acts at each codon position, and the actions the three S₄ are independent from each other—the order of their actions does not matter: the induced permutations of the letters commute—they form a direct product. The direct product (S₄)₁ × (S₄)₂ × (S₄)₃ is a permutation group of order 24³ = 13,824, and a symmetry group of the codon set—the indices (1,2,3) indicate the codon positions upon which each S₄ acts. The wreath product, S₃ x_wreath (S₄)₁ × (S₄)₂ × (S₄)₃, of order 82,944 (=6 × 13,824), is a permutation group acting on the codon set in which S₃ permutes the indices (1,2,3) corresponding with the three codon positions (Section 5.1). The identity of S₃ recovers the direct product (S₄)₁ × (S₄)₂ × (S₄)₃ from the wreath product. The wreath product does not commute, for example: (1 ↔ 2). (A₂ ↔ C₂) ≠ (A₂ ↔ C₂). (1 ↔ 2); the first permutation exchanges codon positions 1 ↔ 2 and then induces A ↔ C at the second position resulting in the exchange A ↔ C at the 2nd codon position, while the second permutation induces A ↔ C at the second position and then exchanges codon positions 1 ↔ 2 resulting in the exchange A ↔ C at the 1st codon position.

In general, a finite group G on an n-set is isomorphic to a subgroup of S_n (Cayley’s theorem), and the order of G divides n!, the order of S_n (by Lagrange’s theorem). In particular, S₆₄ acts on the 64 codons as an indexed set [64], and S₆₄ of order 64! is isomorphic to the largest symmetry group of the codon set as it comprises all [64] → [64] maps. Computation confirms that both the direct product (S₄)₁ × (S₄)₂ × (S₄)₃ and the wreath product S₃ x_wreath (S₄)₁ × (S₄)₂ × (S₄)₃ are subgroups of S₆₄ with (very large) integer indices (index = order 64!/order subgroup), i.e., their order divides 64! exactly.

Appendix C. The Symmetry Group of the Tetrahedron

The tetrahedron symmetry group, or Coxeter A3 group, comprises 12 reflections and 12 rotations and is isomorphic to S₄ (S₄ permutes the four labels of the tetrahedron vertices; S₄ is discussed in Appendix B). The A3 group is generated by reflections in the six tetrahedron symmetry planes, the perpendicular bisectors of the tetrahedron edges, and A3 is thus a reflection or Coxeter group [27]. The 24 symmetries are illustrated with the tetrahedron of Figure 9: the vertex numbers are fixed as reference frame and the vertices/vertex labels {A,C,G,U} moved by the symmetries. The initial labeling (1,2,3,4) = ACGU is changed by the reflection in the M₃₄-mirror plane of Figure 9, the bisector of the {3,4} edge, to (1,2,3,4) = acUG (fixed labels are in small caps): acGU → acUG. The six mirror reflections produce CAgu, GcAu, UcgA, aGCu, aUgC, acUG. Two consecutive reflections in the same mirror give a 0-degree or identity rotation: acgu. The intersections of mirror planes generate rotation axes as two consecutive reflections equate a rotation. Three 180 degree rotation axes run through the centers of opposite tetrahedron edges and opposite faces of the cube of Figure 9. The 180 degree rotations, CAUG, GUAC, and UGCA, are generated by reflections in two orthogonal mirrors, such as the bisectors of {1,2} and {3,4}. The four 60 and 120 degrees rotation axes that run from the tetrahedron vertices through the centers of the opposite triangular faces are diagonals of the cube of Figure 9. For example, the 60 degree counterclockwise rotation around the axis from vertex-1 through the center of the opposite face moves aCGU → aUCG and is generated by reflection in the {3, 4}-bisector plane, acGU → acUG, followed by reflection in the {2, 3}-bisector, aCUg → aUCg. (The four equilateral triangular faces of the tetrahedron possess the symmetries of the triangle, Appendix B and Figure 9). The eight rotation products are aUCG, aGUC, GcUA, UcAG, UAgC, CUgA, CGAu, GACu. Lastly, reflections of the three 180 degree rotation products, CAUG, GUAC, and UGCA, in a mirror planes at a 45 degree angle with the rotation axis produce the remaining six reflection symmetries: UACG, CGUA, CUAG, GAUC, UGAC, and GUCA. For example, CAUG followed by a reflection in the {1,3}-bisector plane gives UACG, as does UGCA followed by reflection in the {2,4}-bisector. As shown above, the 24 different A3 symmetries induce permutations of the tetrahedron labels in one-to-one correspondence with the 24 S₄ permutations of ACGU. Thus, if two A3-symmetries R1, R2 induce permutations p, q, respectively, then R1 followed by R2 induces the permutation p followed by q: A3 and S₄ are isomorphic (Group isomorphism is defined in Appendix B).

Appendix D. The Polytope Product

The polytope product [28,29] is defined for any two polytopes. It is illustrated here for two line segments: segment-A of length-1, defined by vertex set {v1, v2} and space coordinates {(0), (1)}, and segment-B of length-2, defined by vertex set {v3, v4} and coordinates {(0), (2)}. The Cartesian product of the two vertex sets generates four (=2 × 2) vertices {v1v3, v1v4, v2v3, v2v4} with space coordinates {(0,0), (0,2), (1,0), (1,2)} that are the vertices of a rectangle—hence the name rectangular product [28] for the polytope product in Euclidian space. Similarly, the product of any two polytopes P and Q defined by, respectively, p and q vertices, generates (p × q) vertices via the Cartesian product of these vertex sets, and the corresponding product of the space coordinates adds the dimensions of the P and Q polytopes. In this process every edge (line segment) of P forms a rectangular product with every edge of Q as described above. The CodonPolytope is the product of three congruent regular tetrahedrons, and the rectangular product of their congruent edges, one edge of each tetrahedron, forms a cube. (With six edges per tetrahedron, the rectangular product generates 216 = 6³ cubes.)

Appendix E. The CodonPolar Polytope

A cube has an octahedron as polar (dual) partner; the six octahedron vertices are centered on the six faces of the cube. Such polar partners have the same symmetry group, but inverted face vectors and anti-isomorphic face lattices, as discussed below. In fact, every simple polytope has a simplicial polar partner of the same dimension and vice versa [29]. The example above illustrates this: the cube is a simple 3-polytope (as its vertices are incident on three edges, the same number as its dimension), and the octahedron is a simplicial 3-polytope as all its lower dimensional faces (but not the octahedron itself) are simplexes. Simplexes are polytopes for which each subset of two vertices defines an edge. Line segments, triangles and tetrahedrons are, respectively, 1-, 2- and 3-simplexes, and higher dimensional simplexes are formed by adding vertices to a tetrahedron, one vertex per dimension, and connecting these vertices via single edges to all other vertices. As the CodonPolytope is a simple 9-polytope (Section 4.1), it has a simplicial 9-polytope as dual partner—the CodonPolar polytope. The Polar face vector (1, 12, 66, 220, 492, 768, 840, 624, 288, 64, 1) is the inverse of the CodonPolytope face vector (1, 64, 288, …, 66, 12, 1) (Section 4.1). For example, the single empty face (dimension minus-1) of the CodonPolytope corresponds with the CodonPolar 9-polytope itself, and the 64 (congruent, zero dimensional) vertices of the CodonPolytope correspond with the 64 congruent 8-facets of the Polar so that each Polar 8-facet identifies a codon. Table 2 lists all faces of the Polar, which are related to the CodonPolytope faces (listed in Table 1) through the inversion of the face vectors and anti-isomorphism (analogous to inversion) of the face lattices. (Face lattices are ordering by inclusion relationships of polytope faces, such as three vertices are pair-wise contained in three edges, which are contained in a triangle). The CodonPolar is the 9-dimensional convex hull of only 12 vertices in correspondence with the geometric centers of the twelve 8-facets of the CodonPolytope. These 12 vertices span three congruent tetrahedrons, each one living in a different 3-subspace of Euclidian 9-space. The Polar can be realized in 9-space by adding six zero coordinates to the 3D-coordinates of tetrahedron vertices. For example, for the tetrahedron living in the first three dimensions: {(−1,−1,−1, 0, …, 0), (1, 1, −1, 0, …, 0), (−1, 1, 1, 0, … , 0), (1, −1, 1, 0, …, 0)}. These integer Polar vertex coordinates correspond with the 3x-dilated geometric centers of the 8-facets of the CodonPolytope realization of Section 4.2. The 66 edges of the Polar comprise 48 A-edges of Euclidian length √6 between vertices of different tetrahedrons and 18 B-edges of length 2√2 between vertices of the same tetrahedron, see Table 2. These A and B edges are non-congruent 1D-faces and correspond, via the anti-isomorpishm of the face lattices, with the 48 7B-ridges and 18 7A-ridges of the CodonPolytope (Table 1). The CodonPolar’s simplex faces are obtained by adding one vertex per dimension, and the sum of vertices (X + Y + Z) in the 2nd column of Table 2 indicates whether these face vertices are incident on one, two or three of the 3-subspace tetrahedrons, e.g., each vertex of an A-triangle (1 + 1 + 1) is incident on a different tetrahedron, while all vertices of a C-triangle (3 + 0 + 0) are incident on the same tetrahedron. The symmetry group of the Polar is identical to the symmetry group of the CodonPolytope and isomorphic with S₃ x_wreath (A3)₁ × (A3)₂ × (A3)₃, with each A3 acting on a different tetrahedron and different 3-subspace of the 9-space, and S₃ actions permuting the three 3-subspaces and the tetrahedrons and A3-group mirrors contained in them (see Section 4.3 for a more detailed description of this 9-space symmetry group).

Appendix F. Colorings, Colorings Classes, and Color Counting Formulas

The general mathematical theory, and in particular, Burnside’s Lemma, Polya’s enumeration formula and De Bruijn’s generalization of this formula can be found in [36]. The basic coloring concepts are illustrated here for the tetrahedron and two colors, Red (R) and Blue (B)—a “toy” geometric model for a 1-length block code using a four letter alphabet {A, C, G, U} encoding two messages {R,B}, not unlike the family box tetrahedrons of the genetic code encoding two different amino acids (Section 6.2). There are 16 (=2⁴) ways to color the four vertices with two colors; the 16, 2-colorings of the tetrahedron are shown in Figure 14. Take one coloring (R, B, B, B)—vertex-1 Red and the other vertices Blue; the symmetries of the tetrahedron move R to any other vertex: (B, R, B, B), (B, B, R, B) or (B, B, B, R)–3th row of Figure 14, so that all four colorings of one vertex R and three B belong to the same colorings equivalence class 1R3B: all four colorings 1R3B are images of each other—equivalent, under the tetrahedron symmetries, essentially the same coloring. The class colorings pattern 1R3B corresponds with code equivalence class: one code word for Red, three code words for Blue. Similarly, all six colorings of two vertices Red and two Blue (2nd row and last two tetrahedrons of the 1st row of Figure 14) are equivalent under the tetrahedron symmetries and, thus, form a single colorings class with colorings pattern 2R2B. The two colorings classes 4R and 4B are each made up by a single coloring—symmetry operations do not color any vertices differently (first two tetrahedrons of the 1st row of Figure 14). In summary: the tetrahedron symmetries partition the 16, 2-colorings of the tetrahedron into five colorings classes {4R, 3R1B, 2R2B, 1R3B, 4B}, each having a distinct colorings pattern, and containing, respectively {1, 4, 6, 4, 1} different 2-colorings.

Polya’s enumeration formula counts the number of classes (5) and calculates the colorings pattern inventory {4R, 3R1B, 2R2B, 1R3B, 4B}, with the number of classes for each pattern. Note that two classes {4R, 4B} comprise colorings with only one color, and, thus, do not model a code that reaches two messages (R and B). The number of classes with two colors (=3) is obtained by subtraction from Polya’s count of all colorings classes (=5), the number of classes of one color (=2). We call Polya’s enumeration of colorings classes using exactly n colors, a Polya-n-onto count and this number is obtained by iteratively subtracting from Polya’s formula for n colors all Polya-p-onto counts for p = 1, 2, …, (n–2), (n–1). The colorings classes using exactly n colors correspond with equivalence classes of codes reaching n messages (see example below).

Polya’s counting formula is based on the symmetry group of the geometric object, or more precisely, on the isomorphic permutation group of its vertices with all permutations expressed as a cycles—the group’s cycle index. For example for the tetrahedron, the identity permutation I is represented by four singleton cycles of just one vertex (1)(2)(3)(4) as all four tetrahedron vertices are fixed; the 3 ↔ 4 mirror M₃₄ by the 2-cycle in (1)(2)(34), which indicates that vertices 1 and 2 are fixed, but vertices three and four exchanged positions; the rotation of three vertices R₂₄₃ by the 3-cycle in (1)(243), which indicates that vertex 2 moved to the previous position of vertex 4: 2 → 4, 4 →3, and 3 → 2; and the permutation of four vertices P₁₃₂₄ by the 4-cycle (1324), which reads 1 → 3 → 2 → 4 → 1. Let C_n^m indicate m cycles of length n, then these permutations can be abbreviated: I = C₁⁴, M₃₄ = C₁²C₂, R₂₄₃ = C₁C₃, and P₁₃₂₄ = C₄; and the sum of all 24 permutations of S₄ (Appendix B and Appendix C) expressed as the symmetry group’s cycle index: C₁⁴ + 6C₁²C₂ + 3C₂² + 8C₁C₃ + 6C₄. The cycle index of the CodonPolytope symmetry group is given in Appendix G. A permutation leaves a coloring invariant when all vertices permuted by a cycle are the same color, but different cycles can have different colors. This observation forms the basis for Polya’s formula that counts the number of colorings classes: in the group cycle index substitute for C_j the number of colors and divide the total by the group order. For the 2-colorings of the tetrahedron Polya’s formula thus reads: (2⁴ + 6 × 2² × 2 + 3 × 2² + 8 × 2 × 2 + 6 × 2)/24 = 5 colorings classes. The number of colorings of four tetrahedron vertices using one, two, three, and four colors equals 1, 16, 81, and 256 (=n⁴, with n = number of colors); by Polya’s formula these colorings are partitioned into respectively, 1, 5, 15, and 35 colorings classes, but the corresponding number Polya-n-onto colorings classes (see above) is only 1, 3, 3, and 1. (Here we illustrate the iterative subtraction of Polya-p-onto counts for p = 1, … , n–1 to arrive at the Polya-n-onto count: to calculate the Polya-2-onto-count, subtract from the five colorings classes using 2 colors the 2, 1-color classes: 5 − 2 = 3; to calculate the Polya-3-onto count, subtract from the 15 classes all 3, 1-color classes and all 9, 2-onto-colorings (C(3,2) = 3 ways to pick two colors from three colors, and there are three Polya-2-onto classes: 3 × 3 = 9): 15 − 12 = 3; and similarly for the Polya-4-onto count: 35 − 4 × 1 – 6 × 3 − 4 × 3 = 1. The notation C(n,m) indicates the number of ways to choose m out of n, see Appendix A).

Polya’s formula also identifies the colorings pattern inventory and the number of colorings classes per pattern: substitute in the group cycle index for all terms C_n^m, C_n with a color sum (such as R + B for two colors) with each color raised to the power n (so 3C₂² becomes 3(R² + B²)²), then expand and add all terms and divide the result by the group order. For example, the tetrahedron symmetry group of order 24 has cycle index = C₁⁴ + 6C₁²C₂ + 3C₂² + 8C₁C₃ + 6C₄, so that Polya’s formula for two colors R and B equals [(R + B)⁴ + 6(R + B)²(R² + B²) + 3(R² + B²)² + 8(R + B)(R³ + B³) + 6(R⁴ + B⁴)]/24 = R⁴ + R³B + R²B² + B³R + B⁴, which corresponds with the colorings classes inventory {4R, 3R1B, 2R2B, 1R3B, 4B} above, and with only one colorings class per pattern. For comparison, the colorings inventory for a 2-colored square equals R⁴ + R³B + 2R²B² + RB³ + B⁴; it has two R²B² classes in correspondence with two adjacent or two diagonally opposed vertices of the same color—these two different colorings are not equivalent under the symmetry group of the square.

In DeBruijn’s generalization of Polya’s theory [36] color symmetries permute colors and reduce the number of colorings classes in the inventory. For example, the permutation group S₂ acting on the colors Red and Blue exchanges the two colors, they become equivalent (but not the same, they remain distinguishable). The action of S₂ on the colorings inventory of the tetrahedron, {4R, 3R1B, 2R2B, 1R3B, 4B}, renders the two classes 4R and 4B equivalent, they become the single class “all four vertices the same color.” Similarly the classes 3R1B and 1R3B are equivalent under S₂ color symmetry as class “three vertices one color, one vertex the other color,” while the Polya class 2R2B equals the unique DeBruin class “two vertices one color, two vertices the other color”. Thus, the DeBruin’s colorings pattern inventory equals {4, (3,1), (2,2)}, and contains just three classes (instead of Polya’s five classes) that comprise respectively, {2, 8, 6} 2-colorings of the tetrahedron (which are easily identified in Figure 14). The DeBruijn’s counting identifies just two different codes conveying two messages: one code using two code words for each message, and one code using three code words for one message, and one code word for the other. With application to the genetic code, the four GAN codons (represented by the vertices of a tetrahedron face of the CodonPolytope) differ only by the last letter {A, C, G, U}, and {GAA, GAG} encode Glu, while {GAC,GAU} encode Asp, and these codes thus correspond to a two color, 2R2B code according to Polya’s formula, and a (2,2) code according to DeBruin’s enumeration; each code represents a unique Polya or DeBruin code class that contains all mathematically equivalent codes assigning any two GAN codons to Asp and the other two GAN codons to Glu.

Appendix G. The Cycle Indices of the Direct and Wreath Product Groups

The cycle indices of the groups were computed from the group actions on the codon set (Appendix B and Section 5.1). These actions permute the codons and generate the corresponding permutation cycles of the 64 codons. Cycle indices, cycles and their notation are detailed in Appendix F.

Cycle index of the direct product (S₄)₁ × (S₄)₂ × (S₄)₃:

C₁⁶⁴ + 18 C₁³²C₂¹⁶ + 108 C₁¹⁶C₂²⁴ + 216 C₁⁸C₂²⁸ + 657 C₂³² + 24 C₁¹⁶C₃¹⁶ + 192 C₁⁴C₃²⁰ + 512 C₁C₃²¹ + 3096 C₄¹⁶ + 288 C₁⁸C₂⁴C₃⁸C₆⁴ + 1152 C₁²C₂C₃¹⁰C₆⁵ + 864 C₁⁴C₂⁶C₃⁴C₆⁶ + 1224 C₂⁸C₆⁸ + 576 C₂²C₆¹⁰ + 3744 C₄⁴C₁₂⁴ + 1152 C₄C₁₂⁵.

Cycle index of the wreath product: S₃ x_wreath (S₄)₁ × (S₄)₂ × (S₄)₃:

C₁⁶⁴ + 18 C₁³²C₂¹⁶ + 180 C₁¹⁶C₂²⁴ + 648 C₁⁸C₂²⁸ + 873 C₂³² + 24 C₁¹⁶C₃¹⁶ + 1344 C₁⁴C₃²⁰ + 512 C₁C₃²¹ + 432 C₁⁸C₂⁴C₄¹² + 2592 C₁⁴C₂⁶C₄¹² + 1296 C₂⁸C₄¹² + 9576 C₄¹⁶ + 288 C₁⁸C₂⁴C₃⁸C₆⁴ + 1152 C₁²C₂C₃¹⁰C₆⁵ + 1440 C₁⁴C₂⁶C₃⁴C₆⁶ + 1224 C₂⁸C₆⁸ + 576 C₁⁴C₃⁴C₆⁸ + 4608 C₁C₃⁵C₆⁸ + 10368 C₁²C₂C₃²C₆⁹ + 5760 C₂²C₆¹⁰ + 6912 C₈⁸ + 9216 C₁C₉⁷ + 3456 C₁²C₂C₃²C₄³C₆C₁₂³ + 5472 C₄⁴C₁₂⁴ + 11520 C₄C₁₂⁵ + 3456 C₈²C₂₄².

Appendix H. Coloring Computations

The number of code classes of [64] → [21] codes equals the number of different Polya-21-onto colorings classes of the CodonPolytope—the number of classes of colorings of the polytope with exactly 21 colors (and not with fewer than 21 colors) (Section 7.3). The calculation of Poly-21-onto colorings based on Polya’s counting formula of all colorings is detailed in Appendix F; the cycle index of the CodonPolytope symmetry group of order 82,944, and isomorphic with S₃ x_wreath (S₄)₁ × (S₄)₂ × (S₄)₃ is given in Appendix G. Polya’s count of the colorings classes equals substitution of the number of colors in the cycle index with division of the result by the group order (Appendix F). The results of the iterative computations of Polya-p-onto colorings, for p = 1, … , 21, are given in Table 3. The number of code classes of [64] → [21] codes equals 1.82 × 10⁷⁹ (Section 7.3) about 36% of all 5.05 × 10⁷⁹ Polya colorings classes of the CodonPolytope using 21 (and fewer) colors.

Polya’s formula also counts the number classes using the colorings pattern of the genetic code: one vertex “colored” with Met, one with Trp; two vertices each with Asp, Asn, Cys, Gln, Glu, His, Lys, Phe, and Tyr; three vertices each with Ile and Stop; four vertices each with Ala, Gly, Pro, Thr, and Val; six vertices each with Arg, Leu, and Ser (the messages are the colors, Section 7.4); this pattern corresponds with the set partition 1²2⁹3²4⁵6³ of [64] (Section 7.5). The formula requires substitution of these 21 colors in the group cycle index with expansion of the terms and division of the total by the group order (Appendix F). In this calculation the first term of the cycle index C₁⁶⁴ evaluates as the multinomial coefficient M(64, 1²2⁹3²4⁵6³) = 64!/(1!² × 2!⁹ × 3!² × 4!⁵ × 6!³) ≈ 2.316 × 10⁶⁹ (Appendix A), and this term dominates all other terms of the cycle index: The 2nd term 18 C₁³²C₂¹⁶ evaluates to a smaller number than 18 × 32! × 16! ≤ 10⁵⁰ (because the denominator evaluates to greater than 1) and the remaining terms are even smaller so that even the sum of these terms can be neglected in the calculation. The number of code classes of [64] → [21] codes with the same code pattern as the genetic code thus equals 2.79 × 10⁶⁴ = 2.316 × 10⁶⁹/82,944, or M(64, 1²2⁹3²4⁵6³)/group order (Section 7.4). Similar calculations with Polya’s formula for codes with colorings patterns corresponding with binary divisions of [64] such as those related with the codon polytope splitting model for the evolution of the code (Section 6.5): two colors for 32 codons each, corresponding with the set partition 32², and for four colors for 16 codons each or 16⁴, and 8⁸, and 16⁴ and 32² showed that the number of code classes using these patterns equals, respectively, 2.21 × 10¹³, 7.98 × 10³⁰, 2.19 × 10⁴⁷, 1.26 × 10⁶², and 3.56 × 10⁷⁴.

References

Knight, R.D.; Freeland, S.J.; Landweber, L.F. Rewiring the keyboard: Evolvability of the genetic code. Nat. Rev. Genet. 2001, 2, 49–58. [Google Scholar] [CrossRef] [PubMed]
Koonin, E.V.; Novozhilov, A.S. Origin and evolution of the genetic code: The universal enigma. IUBMB Life 2009, 61, 99–111. [Google Scholar] [CrossRef] [PubMed]
Atkins, J.F.; Gesteland, R.F.; Cech, R. RNA Worlds; Cold Spring Harbor Laboratory Press: Cold Spring Harbor, NY, USA, 2011. [Google Scholar]
Deamer, D.; Szostak, J.W. The Origins of Life; Cold Spring Harbor Laboratory Press: Cold Spring Harbor, NY, USA, 2010. [Google Scholar]
Woese, C.R. Order in the genetic code. Proc. Natl. Acad. Sci. USA 1965, 54, 71–75. [Google Scholar] [CrossRef] [PubMed]
Crick, F.H.C. The origin of the genetic code. J. Mol. Biol. 1968, 38, 367–379. [Google Scholar] [CrossRef]
Woese, C.R.; Dugre, D.H.; Saxinger, W.C.; Dugre, S.A. On the Fundamental Nature and Evolution of the Genetic Code. Cold Spring Harbour Symp. Quant. Biol. 1966, 31, 723–736. [Google Scholar] [CrossRef]
Stephenson, J.D.; Freeland, S.J. Unearthing the root of amino acid similarity. J. Mol. Evol. 2013, 77, 159–169. [Google Scholar] [CrossRef]
Pretzel, O. Error-Correcting Codes and Finite Fields; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
Hamming, R.W. Error detecting and error correcting codes. Bell Lab. Record. 1950, 28, 193–198. [Google Scholar] [CrossRef]
Thompson, T.M. From Error Correcting Codes through Sphere Packing to Simple Groups; The Mathematical Association of America: Washington, DC, USA, 1983. [Google Scholar]
He, M.X.; Petoukhov, S.V.; Ricci, P.E. Genetic code, Hamming Distance and Stochastic Matrices. Bull. Math. Biol. 2004, 66, 1405–1421. [Google Scholar] [CrossRef] [PubMed]
Sánchez, R.; Morgado, E.; Grau, R.A. Genetic code Boolean structure. I. The meaning of Boolean deductions. Bull. Math. Biol. 2005, 67, 1–14. [Google Scholar] [CrossRef] [PubMed]
Jiménez-Montaño, M.A. The fourfold way of the genetic code. BioSystems 2009, 98, 105–114. [Google Scholar] [CrossRef]
Crowder, T.; Li, C.-K. Studying the Genetic Code by a Matrix Approach. Bull. Math. Biol. 2010, 72, 953–972. [Google Scholar] [CrossRef]
José, M.V.; Morgado, E.R.; Govezensky, T. Genetic Hotels for the Standard Genetic Code: Evolutionary Analysis Based upon Novel Three-Dimensional Algebraic Models. Bull. Math. Biol. 2011, 73, 1443–1476. [Google Scholar] [CrossRef] [PubMed]
Jiménez-Montaño, M.A.; de la Mora-Basáñez, C.R.; Pöschel, T. The hypercube structure of the genetic code explains conservative and non-conservative aminoacid substitutions in vivo and in vitro. BioSystems 1996, 39, 117–125. [Google Scholar] [CrossRef]
Karesev, V.A.; Stefanov, V.E. Topological Nature of the Genetic Code. J. Theor. Biol. 2001, 209, 303–317. [Google Scholar] [CrossRef] [PubMed]
José, M.V.; Morgado, E.R.; Govezensky, T. An Extended RNA Code and its Relationship to the Standard Genetic Code: An Algebraic and Geometrical Approach. Bull. Math. Biol. 2007, 69, 215–243. [Google Scholar] [CrossRef] [PubMed]
Frappat, L.; Sciarrino, A.; Sorba, P. A crystal base for the genetic code. Phys. Lett. A 1998, 250, 214–221. [Google Scholar] [CrossRef]
Antoneli, F.; Forger, M.; Gaviria, P.A.; Hornos, J.E.M. On amino acid and codon assignment in algebraic models for the genetic code. Int. J. Modern Phys. B 2010, 24, 435–463. [Google Scholar] [CrossRef]
Bashford, J.D.; Tsohantjis, I.; Jarvis, P.D. A supersymmetric model for the evolution of the genetic code. Proc. Natl. Acad. Sci. USA 1998, 95, 987–992. [Google Scholar] [CrossRef] [PubMed]
Antoneli, F.; Forger, M. Symmetry breaking in the genetic code: Finite Groups. Math. Comput. Model. 2011, 53, 1469–1488. [Google Scholar] [CrossRef]
Lenstra, R. Evolution of the genetic code through progressive symmetry breaking. J. Theor. Biol. 2014, 347, 95–108. [Google Scholar] [CrossRef] [PubMed]
Mazur, D.R. Combinatorics, A guided Tour; The Mathematical Association of America Inc.: Washington, DC, USA, 2010. [Google Scholar]
Liboff, R.L. Primer for Point and Space Groups; Springer Verlag New York Inc.: New York, NY, USA, 2004. [Google Scholar]
Grove, L.C.; Benson, C.T. Finite Reflection Groups. Graduate Texts in Mathematics 99; Springer Verlag New York Inc.: New York, NY, USA, 1985. [Google Scholar]
Robertson, S.A. Polytopes and Symmetry. London Mathematical Society Lecture Note Series 90; Cambridge Univeristy Press: Cambridge, UK, 1984. [Google Scholar]
Ziegler, G.M. Lectures on Polytopes. Graduate Texts in Mathematics 152; Springer Verlag New York Inc.: New York, NY, USA, 2007. [Google Scholar]
Passman, D.S. Permutation Groups; Dover Publications Inc.: Mineola, NY, USA, 2012. [Google Scholar]
Rotman, J.J. An Introduction to the Theory of Groups. Graduate Texts in Mathematics 148; Springer-Verlag New York Inc.: New York, NY, USA, 1995. [Google Scholar]
Gilmore, R. Lie Groups, Physics, and Geometry; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
Knight, R.D.; Freeland, S.J.; Landweber, L.F. Selection, history and chemistry: The three faces of the genetic code. Trends Biochem. Sci. 1999, 24, 241–247. [Google Scholar] [CrossRef]
Grosjean, H.; de Grécy-Lagard, V.; Marck, C. Review. Deciphering synonymous codons in the three domains of life: Co-evolution with specific tRNA modification enzymes. Febs Lett. 2010, 584, 252–264. [Google Scholar] [CrossRef] [PubMed]
Graham, J.H.; Raz, S.; Hel-Or, H.; Nevo, E. Fluctuating asymmetry: Methods, theory and applications. Symmetry 2010, 2, 466–540. [Google Scholar] [CrossRef]
Harris, J.M.; Hirst, J.L.; Mossinghoff, M.J. Combinatorics and Graph Theory; Springer: New York, NY, USA, 2008. [Google Scholar]
Jungck, J.R. The genetic code as a periodic table. J. Mol. Evol. 1978, 11, 211–224. [Google Scholar] [CrossRef] [PubMed]
Lehman, J. Physico-chemical constraints connected with the coding properties of the genetic system. J. Theor. Biol. 2000, 202, 129–144. [Google Scholar] [CrossRef] [PubMed]
Tlusty, T. A colorful origin for the genetic code: Information theory, statistical mechanics and the emergence of molecular codes. Phys. Life Rev. 2010, 7, 362–376. [Google Scholar] [CrossRef] [PubMed]
Dragovich, B.; Dragovich, A. p-Adic modeling of the genome and the genetic code. Comput. J. 2010, 53, 432–441. [Google Scholar] [CrossRef]
shCherbak, V.I. Arithmetic inside the universal genetic code. Biosystems 2003, 70, 187–209. [Google Scholar] [CrossRef]
Jungck, J.R. Genetic codes as codes: Towards a theoretical basis for bioinformatics. In BIOMAT 2008; Mondani, R.P., Ed.; World Scientific Publishing: Singapore, 2009; pp. 300–337. [Google Scholar]
Tlusty, T. A model for the emergence of the genetic code as a transition in a noisy information channel. J. Theor. Biol. 2007, 249, 331–342. [Google Scholar] [CrossRef] [PubMed]
Chechetkin, V.R. Block structure and stability of the genetic code. J. Theor. Biol. 2003, 222, 177–188. [Google Scholar] [CrossRef]
Eigen, M. From Strange Simplicity to Complex Familiarity. A Treatise on Matter, Information, Life and Thought; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
He, P.-A.; Li, D.; Zhang, Y.; Wang, X.; Yao, Y. A 3D graphical representation of protein sequences based on the Gray code. J. Theor. Biol. 2012, 304, 81–87. [Google Scholar] [CrossRef] [PubMed]
José, M.V.; Morgado, E.R.; Guimaraes, R.C.; Zamudio, G.S.; de Farias, S.T.; Bobadilla, J.R.; Sosa, D. Three-dimensional algebraic models of the tRNA code and 12 graphs for representing amino acids. Life 2014, 4, 341–373. [Google Scholar] [CrossRef] [PubMed]
Sánchez, R.; Grau, R.; Morgado, E. A novel Lie algebra of the genetic code over the Galois field of four DNA bases. Math. Biosci. 2006, 202, 156–174. [Google Scholar] [CrossRef] [PubMed]
Trainor, L.E.H.; Rowe, G.W.; Szabo, V.L. A tetrahedral representation of poly-codon sequences and a possible origin of codon degeneracy. J. Theor. Biol. 1984, 108, 459–468. [Google Scholar] [CrossRef]
Jestin, J.-L.; Soulé, C. Symmetries by base substitutions in the genetic code predict 2′ or 3′ aminoacylation of tRNAs. J. Theor. Biol. 2007, 247, 391–494. [Google Scholar] [CrossRef] [PubMed]
Jestin, J.-L. Degeneracy in the genetic code and its symmetries by base substitutions. C. R. Biol. 2006, 329, 168–171. [Google Scholar] [CrossRef] [PubMed]
Danckwerts, H.J.; Neubert, D. Symmetries of genetic code-doublets. J. Mol. Evol. 1975, 5, 327–332. [Google Scholar] [CrossRef] [PubMed]
Findley, G.L.; Findley, A.M.; McGlynn, S.P. Symmetry characteristics of the genetic code. Proc. Nat. Acad. Sci. USA 1982, 79, 7061–7065. [Google Scholar] [CrossRef] [PubMed]
Bertman, M.O.; Jungck, J.R. Group graph of the genetic code. J. Hered. 1979, 70, 379–384. [Google Scholar] [PubMed]
Massey, S.E. A sequential “2-1-3” model of the genetic code evolution that explains codon constraints. J. Mol. Evol. 2006, 62, 809–810. [Google Scholar] [CrossRef] [PubMed]
Trifonov, E.N. Consensus temporal order of amino acids and evolution of the triplet code. Gene 2000, 261, 139–151. [Google Scholar] [CrossRef]
Higgs, P.G. A four-column theory for the origin of the genetic code: Tracing the evolutionary pathways that gave rise to an optimized code. Biol. Direct 2009, 4. [Google Scholar] [CrossRef] [PubMed]
Di Giulio, M. The coevolution theory of the origin of the genetic code. Phys. Life Rev. 2004, 1, 128–137. [Google Scholar] [CrossRef]
Wong, J.T. Coevolution theory of the genetic code at age thirty. BioEssays 2005, 27, 416–425. [Google Scholar] [CrossRef] [PubMed]
De Pouplana, L.R.; Schimmel, P. Aminoacyl-tRNA synthetases: Potential markers of genetic code development. Trends Biochem. Sci. 2001, 26, 591–596. [Google Scholar] [CrossRef]
Delarue, M. An asymmetric underlying rule in the assignment of codons: Possible clue to a quick early evolution of the genetic code via successive binary choices. RNA 2007, 13, 161–169. [Google Scholar] [CrossRef] [PubMed]
Rodin, S.N.; Rodin, A.S. On the origin of the genetic code: Signatures of its primordial complementarity in tRNAs and aminoacyl-tRNA synthetases. Heridity 2008, 100, 341–355. [Google Scholar] [CrossRef] [PubMed]
Santos, J.; Monteagudo, A. Study of the genetic code adaptability by means of a genetic algorithm. J. Theor. Biol. 2010, 264, 854–865. [Google Scholar] [CrossRef] [PubMed]
Buhrman, H.; van der Gulik, P.T.S.; Kelk, S.M.; Koolen, W.M.; Stougie, L. Some mathematical refinements concerning error minimization in the genetic code. IEEE/ACM Trans. Comput. Biol. BioInform. 2011, 8, 1358–1372. [Google Scholar] [CrossRef] [PubMed]
Bashford, J.D.; Jarvis, P.D. Spectroscopy of the genetic code. In Quantum Aspects of Life; Abbott, D., Davies, P.C.W., Pati, A.K., Eds.; Imperial College Press: London, UK, 2008; pp. 147–186. [Google Scholar]
Freeland, S.J.; Wu, T.; Keulmann, N. The case for an error minimizing standard genetic code. Orig. Life Evol. Biosph. 2003, 33, 457–477. [Google Scholar] [CrossRef] [PubMed]
Frappat, L.; Sciarrino, A.; Sorba, P. Crystalizing the genetic code. J. Biol. Phys. 2001, 27, 1–34. [Google Scholar] [CrossRef] [PubMed]
Sciarrino, A.; Sorba, P. A minimum principle in codon-anticodon interaction. BioSystems 2012, 107, 113–119. [Google Scholar] [CrossRef] [PubMed]
Sciarrino, A.; Sorba, P. Codon-anticodon interaction and the genetic code evolution. BioSystems 2013, 111, 175–180. [Google Scholar] [CrossRef] [PubMed]
Yockey, H.P. Information Theory, Evolution, and the Origin of Life; Cambridge University Press: New York, NY, USA, 2005. [Google Scholar]

© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).

Share and Cite

MDPI and ACS Style

Lenstra, R. The Graph, Geometry and Symmetries of the Genetic Code with Hamming Metric. Symmetry 2015, 7, 1211-1260. https://doi.org/10.3390/sym7031211

AMA Style

Lenstra R. The Graph, Geometry and Symmetries of the Genetic Code with Hamming Metric. Symmetry. 2015; 7(3):1211-1260. https://doi.org/10.3390/sym7031211

Chicago/Turabian Style

Lenstra, Reijer. 2015. "The Graph, Geometry and Symmetries of the Genetic Code with Hamming Metric" Symmetry 7, no. 3: 1211-1260. https://doi.org/10.3390/sym7031211

APA Style

Lenstra, R. (2015). The Graph, Geometry and Symmetries of the Genetic Code with Hamming Metric. Symmetry, 7(3), 1211-1260. https://doi.org/10.3390/sym7031211

Article Menu

The Graph, Geometry and Symmetries of the Genetic Code with Hamming Metric

Abstract

1. Introduction

2. Preliminaries

2.1. The Code Function

2.2. The Hamming Distances between the 64 Codons of the Codon Set

2.3. The CodonGraph, a Graph Representation of the Codon Set with Hamming Metric

2.4. From Graph to Geometry

2.5. Permutation Symmetries of Graphs and Euclidian Symmetries of Geometric Objects

3. The CodonArray Embedding of the CodonGraph

4. The Geometric Model: The CodonPolytope

4.1. The Construction and Characterization of the CodonPolytope

4.2. A Realization of the CodonPolytope

4.3. The Point Symmetry Group of the CodonPolytope

4.4. Symmetries of the Polytope Faces

5. The Symmetries of the CodonGraph and Codon Set

5.1. The Symmetries of the Codon Set That Preserve Hamming Distances

5.2. The Symmetries of the CodonGraph

6. Symmetries of the Genetic Code

6.1. Exact and Near Symmetries of the Code

6.2. Conservative and Anti-Conservative Symmetries of the Code

6.3. Stronger and Weaker Symmetries of the Code

6.4. Code Symmetries are Not Random

6.5. The CodonPolytope Splitting Model for the Evolution of the Code

7. Codes Represented by Colorings of the Codon Polytope

7.1. CodonPolytope Colorings as Code Models

7.2. The Genetic Code Represents a Class of 41,472 Equivalent Codes

7.3. Counting all Classes of Codes Conveying 21 Messages

7.4. Counting All Code Classes that Share the Pattern of the Genetic Code

7.5. Colorings Classes under Color Symmetries

8. Discussion

Acknowledgments

Conflicts of Interest

Appendix A. Some Discrete Mathematics, Notation and a Few Combinatorial Formulas

Appendix B. Permutations, Groups and Group Isomorphisms

Appendix C. The Symmetry Group of the Tetrahedron

Appendix D. The Polytope Product

Appendix E. The CodonPolar Polytope

Appendix F. Colorings, Colorings Classes, and Color Counting Formulas

Appendix G. The Cycle Indices of the Direct and Wreath Product Groups

Appendix H. Coloring Computations

References

Share and Cite

Article Metrics

Article Access Statistics

Further Information

Guidelines

MDPI Initiatives

Follow MDPI