Insights on Determining Improved Conditions for Multipurpose Reagent Dosing to Increase Froth Flotation Efficiency: NaSH in Cu-Mo Selective Flotation Case Study
Abstract
:1. Introduction
2. Materials and Methods
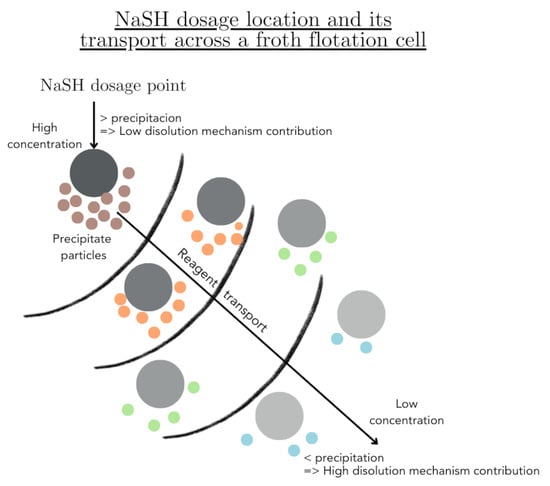
2.1. Eh and pH Monitoring during NaSH Dosing
2.2. NaSH Dosing Tests Leading towards Precipitate Characterisation
3. Results
3.1. Eh and pH Monitoring during NaSH Dosing
3.2. Test B. Precipitate Characterisation
3.3. Modelling and Discussion
3.3.1. Thermodynamics
3.3.2. Conservation Equations
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Wang, D.; Liu, Q. Hydrodynamics of Froth Flotation and its Effects on Fine and Ultrafine Mineral Particle Flotation: A Literature Review. Miner. Eng. 2021, 173, 107220. [Google Scholar] [CrossRef]
- Arbiter, N.; Harris, C.C.; Yap, R.F. The air flow number in flotation machine scale-up. Int. J. Miner. Process. 1976, 3, 257–280. [Google Scholar] [CrossRef]
- Mankosa, M.J. Scale-Up of Column Flotation. Ph.D. Thesis, Faculty of the Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 1990; p. 371. [Google Scholar]
- Yianatos, J.B.; Henríquez, F.D.; Oroz, A.G. Characterization of large size flotation cells. Miner. Eng. 2005, 19, 531–538. [Google Scholar] [CrossRef]
- Kelsall, D.F. Application of probability in the assessment of flotation systems. IMM Trans. 1961, 70, 191–204. [Google Scholar]
- Truter, M. Scale-Up of Mechanically Agitated Flotation Processes Based on the Principles of Dimensional Similitude. MSc Thesis, Department of Process Engineering at the University of Stellenbosch, Stellenbosch, South Africa, 2010; p. 187. [Google Scholar]
- Gochin, R.J.; Smith, M.R. The methodology of froth flotation test work. In Mineral Processing Design; Yarar, B., Dogan, Z.M., Eds.; NATO ASI Series; Springer: Dordrecht, The Netherlands, 1987; Volume 122, pp. 166–201. [Google Scholar]
- Cases, J.M.; Villieras, F. The mechanisms of collector adsorption-desorption (ionic and non-ionic surfactants) on heterogeneous surfaces. In Innovations in Flotation Technology; Mavros, P., Matis, K.A., Eds.; Springer: Dordrecht, The Netherlands, 1992; pp. 25–56. [Google Scholar]
- Somasundaran, P.; Ramachandran, R. Surfactants in Flotation. In Surfactants in Chemical/Process Engineering; Surfactant Science Series No 28; Wasan, D.T., Ginn, M.E., Shah, D.O., Eds.; Routledge: New York, NY, USA, 1988; Chapter 6; pp. 195–235. [Google Scholar]
- Pradip; Fuerstenau, D.W. The role of inorganic and organic reagents in the flotation separation of rare-earth ores. Int. J. Miner. Process. 1991, 32, 1–22. [Google Scholar] [CrossRef]
- Heinrich Schubert, H.; Bischofberger, C. On the hydrodynamics of flotation machines. Int. J. Miner. Process. 1978, 5, 131–142. [Google Scholar] [CrossRef]
- Nagata, S. Mixing: Principles and Applications; Halsted Press: New York, NY, USA, 1975; p. 458. [Google Scholar]
- Gupta, C.K. Extractive Metallurgy of Molybdenum; CRC Press: Boca Raton, FL, USA, 2000; p. 404. [Google Scholar]
- Nagaraj, D.R.; Gorken, A. Potential controlled flotation and depression of copper sulphides and oxides using hydrosulphide in non-xanthate systems. In Processing of Complex Ores, Proceedings of the International Symposium on Processing of Complex Ores, Proceedings of Metallurgical Society of Canadian Institute of Mining and Metallurgy, Halifax, NS, Canada, 20–24 August 1989; Elsevier: Amsterdam, The Netherlands, 1989; pp. 203–213. [Google Scholar]
- Chander, S. Oxidation/Reduction Effects in Depression of Sulfide Minerals—A Review. Min. Metall. Explor. 1985, 2, 26–35. [Google Scholar] [CrossRef]
- Goktepe, F. Effect of H2O2 and NaSH Addition to Change the Electrochemical Potential in Flotation of Chalcopyrite and Pyrite Minerals. Miner. Process. Extr. Metall. Rev. Int. J. 2010, 32, 24–29. [Google Scholar] [CrossRef]
- Rousseau, W. Handbook of Separation Process Technology; Wiley: Hoboken, NJ, USA, 1987; p. 1024. [Google Scholar]
- Wills, B.A.; Finch, J.A. Wills’ Mineral Processing Technology: An Introduction to the Practical Aspects of Ore Treatment and Mineral Recovery; Elsevier: Amsterdam, The Netherlands, 2015; p. 512. [Google Scholar]
- Kalichini, M.S. A Study of the Flotation Characteristics of a Complex Copper Ore. MSc Thesis, University of Cape Town, Cape Town, South Africa, 2015; p. 178. [Google Scholar]
- Yin, W.Z.; Zhang, L.R.; Ding, Y.Z. Research on Potential Control Flotation of Molybdenite. Adv. Mater. Res. 2009, 58, 147–153. [Google Scholar] [CrossRef]
- Aydin, S.B.; Gul, A. Optimization of flotation parameters for beneficiation of a molybdenum ore. Physicochem. Probl. Miner. Process. 2017, 53, 524–540. [Google Scholar]
- Mehrabani, J.V.; Pourghahramani, P.; Asqarian, H.; Bagherian, A. Effects of Ph and pulp potential on selective separation of Molybdenite from the Sungun Mine Cu-Mo concentrate. Int. J. Min. Geo-Eng. 2017, 51, 147–150. [Google Scholar]
- Brenet, J. Introduction a L’electrochimie de L’equilibre et du non Equilibre; Masson: Paris, France, 1980; p. 155. [Google Scholar]
- Eliaz, N.; Gileadi, E. Physical Electrochemistry: Fundamentals, Techniques, and Applications, 2nd ed.; Wiley-VCH: Hoboken, NJ, USA, 2019; p. 452. [Google Scholar]
- Montes-Atenas, G. Role of Composition and Structure of Oxidation Surface Layer of Iron in Decomposition of Differently Structured Azo-Dyes. Kinetics and Reaction Pathways. Ph.D. Thesis, Institut National Polytechnique de Lorraine (INPL), Nancy, France, 2004; p. 189. [Google Scholar]
- Charlot, G.; Badoz-Lambling Mme, J.; Tremillon, B. Les Reactions Electrochimiques. Les Méthodes Electrochimiques d’Analyse; Masson: Paris, France, 1959; p. 395. [Google Scholar]
- Werner, J.; Belz, M.; Klein, K.-F.; Sun, T.; Grattan, K.T.V. Characterization of a fast response fiber-optic pH sensor and illustration in a biological application. Analyst 2021, 146, 4811–4821. [Google Scholar] [CrossRef] [PubMed]
- Rumble, J.R. CRC Handbook of Chemistry and Physics, 100th ed.; CRC Press: Boca Raton, FL, USA, 2019; p. 1554. [Google Scholar]
- Zemaitis, J.F., Jr.; Clark, D.M.; Rafal, M.; Scrivner, N.C. Handbook of Aqueous Electrolyte Thermodynamics: Theory and Application; Wiley: Hoboken, NJ, USA, 1986; p. 478. [Google Scholar]
- Jones, L.; Atkins, P. Chemistry. Molecules, Matter and Change, 4th ed.; W.H. Freeman and Co.: New York, NY, USA, 1989; p. 998. [Google Scholar]
- Karapetiantz, M. Initiation à la Théorie des Phénomènes Chimiques; Traduit du russe par A.Anissimov Editions Mir: Moscow, Russia, 1978; p. 329. [Google Scholar]
- Ekberg, C.; Brown, P.L. Hydrolysis of Metal Ions; Wiley-VCH Verlag GmbH and Co. KGaA: Weinheim, Germany, 2016; p. 952. [Google Scholar]
- Schwertmann, U.; Cornell, R.M. Iron Oxides in the Laboratory: Preparation and Characterizzation, 2nd ed.; Wiley-VCH: Hoboken, NJ, USA, 2000; p. 188. [Google Scholar]
- Lambert, I. An evaluation of the solubility of calcium hydroxide in water and in various aqueous solutions. In Alkaline Earth Hydroxides in Water and Aqueos Solutions; IUPAC Solubility Data Series; Pergamon Press: Oxford, UK, 1992; pp. 112–247. [Google Scholar]
- Pourbaix, M. Atlas of Electrochemical Equilibria in Aqueous Solutions; Franklin, J.A., Translator; National Association of Corrosion Engineers (NACE): Houston, TX, USA, 1974; p. 645. [Google Scholar]
- Brookins, D.G. Eh-pH Diagrams for Geochemistry; Springer: Berlin/Heidelberg, Germany, 1988; p. 176. [Google Scholar]
- Blais, J.F.; Djedidi, Z.; Cheikh, R.B.; Tyagi, R.D.; Mercier, G. Metals Precipitation from Effluents: Review. Pract. Period. Hazard. Toxic Radioact. Waste Manag. 2008, 12, 135–149. [Google Scholar] [CrossRef]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena; John Wiley and Sons: Hoboken, NJ, USA, 2002; p. 895. [Google Scholar]
- Bazanat, M.Z.; Stone, H.A. A two-species reaction-diffusion problem with one static reactant: The case of higher order kinetics. In Nonlinear PDE’s in Condensed Matter and Reactive Flows; NATO, Series C: Mathematical and Physical Sciences; Springer: Dordrecht, The Netherlands, 1999; Volume 569, pp. 1–10. [Google Scholar]
- Harmandas, N.G.; Koutsoukos, P.G. The formation of iron (II) sulfides in aqueous solutions. J. Cryst. Growth 1996, 167, 719–724. [Google Scholar] [CrossRef]
- Szynkarczuk, J.; Komorowski, P.G.; Donini, J.C. Redox reactions of hydrosulphide ions on the platinum electrode—II. An impedance spectroscopy study and identification of the polysulphide intermediates. Electrochim. Acta 1995, 40, 487–494. [Google Scholar] [CrossRef]








| (8) | ||
| (9) | ||
| (10) | ||
| (11) | ||
| (12) | ||
| (13) | ||
| (14) | ||
| (15) | ||
| (16) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernandez, B.; Montes-Atenas, G.; Valenzuela, F.; Yarmuch, J.L. Insights on Determining Improved Conditions for Multipurpose Reagent Dosing to Increase Froth Flotation Efficiency: NaSH in Cu-Mo Selective Flotation Case Study. Minerals 2024, 14, 240. https://doi.org/10.3390/min14030240
Fernandez B, Montes-Atenas G, Valenzuela F, Yarmuch JL. Insights on Determining Improved Conditions for Multipurpose Reagent Dosing to Increase Froth Flotation Efficiency: NaSH in Cu-Mo Selective Flotation Case Study. Minerals. 2024; 14(3):240. https://doi.org/10.3390/min14030240
Chicago/Turabian StyleFernandez, Braulio, Gonzalo Montes-Atenas, Fernando Valenzuela, and Juan Luis Yarmuch. 2024. "Insights on Determining Improved Conditions for Multipurpose Reagent Dosing to Increase Froth Flotation Efficiency: NaSH in Cu-Mo Selective Flotation Case Study" Minerals 14, no. 3: 240. https://doi.org/10.3390/min14030240
APA StyleFernandez, B., Montes-Atenas, G., Valenzuela, F., & Yarmuch, J. L. (2024). Insights on Determining Improved Conditions for Multipurpose Reagent Dosing to Increase Froth Flotation Efficiency: NaSH in Cu-Mo Selective Flotation Case Study. Minerals, 14(3), 240. https://doi.org/10.3390/min14030240