The Process of the Intensification of Coal Fly Ash Flotation Using a Stirred Tank
Abstract
:1. Introduction
2. Methodology
2.1. Geometry Structure
2.2. Governing Equations
2.3. Numerical Methods
2.4. The Post-Processing of the LES Results
3. Numerical Simulation Results and Discussion
3.1. Mean Velocity
3.2. Turbulent Kinetic Energy
3.3. Flow Rate Balance
3.4. Trailing Vortices behind the Blades
3.5. Power Consumption under Different Rotation Speeds
3.6. Turbulent Length Scale
4. Conditioning-Flotation Experiments
4.1. Materials and Methods
4.2. Experimental Results and Discussion
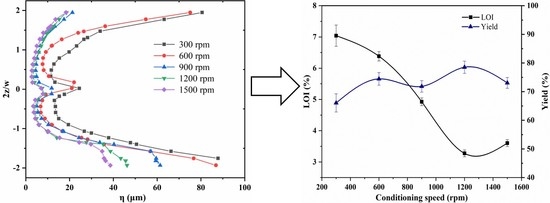
4.2.1. Effect of the Conditioning Speed on the LOI and Yield of Flotation Tailings
4.2.2. Effect of the Conditioning Speed on the RUC of Flotation Concentrates
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xu, Z.; Liu, J.; Choung, J.W.; Zhou, Z. Electrokinetic study of clay interactions with coal in flotation. In. J. Miner. Process. 2003, 68, 183–196. [Google Scholar] [CrossRef]
- Hartuti, S.; Hanum, F.F.; Takeyama, A.; Kambara, S. Effect of Additives on Arsenic, Boron and Selenium Leaching from Coal Fly Ash. Minerals 2017, 7, 99. [Google Scholar] [CrossRef]
- Li, S.; Wu, W.; Li, H.; Hou, X. The direct adsorption of low concentration gallium from fly ash. Sep. Technol. 2016, 51, 395–402. [Google Scholar] [CrossRef]
- ASTM D7348-13, Standard Test Methods for Loss on Ignition (LOI) of Solid Combustion Residues; ASTM International: West Conshohocken, PA, USA, 2013.
- Fly Ash Used for Cement and Concrete; PRC National Standard; Standardization Administration of the People’s Republic of China: Beijing, China, 2017; GB/T 1596-2017.
- Bartoňová, L. Unburned carbon from coal combustion ash: An overview. Fuel Process. Technol. 2015, 134, 136–158. [Google Scholar] [CrossRef]
- Cameán, I.; Garcia, A.B. Graphite materials prepared by HTT of unburned carbon from coal combustion fly ashes: Performance as anodes in lithium-ion batteries. J. Power Sources 2011, 196, 4816–4820. [Google Scholar] [CrossRef]
- Cao, Y.; Li, G.; Liu, J.; Zhang, H.; Zhai, X. Removal of unburned carbon from fly ash using a cyclonic-static microbubble flotation column. J. S. Afr. I. Min. Metall. 2012, 112, 891–896. [Google Scholar]
- An, M.; Liao, Y.; Zhao, Y.; Li, X.; Lai, Q.; Liu, Z.; He, Y. Effect of frothers on removal of unburned carbon from coal-fired power plant fly ash by froth flotation. Sep. Sci. Technol. 2018, 53, 535–543. [Google Scholar] [CrossRef]
- Peng, Y.; Grano, S. Effect of iron contamination from grinding media on the flotation of sulphide minerals of different particle size. Int. J. Miner. Process. 2010, 97, 1–6. [Google Scholar] [CrossRef]
- Piñeres, J.; Barraza, J. Energy barrier of aggregates coal particle-bubble through the extended DLVO theory. Int. J. Miner. Process. 2011, 93, 14–20. [Google Scholar] [CrossRef]
- Hao, J.; Gao, Y.; Khoso, S.; Ji, W.Y.; Hu, Y.H. Interpretation of Hydrophobization Behavior of Dodecylamine on Muscovite and Talc Surface through Dynamic Wettability and AFM Analysis. Minerals 2018, 8, 391. [Google Scholar]
- Sun, W.; Xie, Z.J.; Hu, Y.H.; Deng, M.J.; Yi, L.; He, G.Y. Effect of high intensity conditioning on aggregate size of fine sphalerite. T. Nonferr. Metals. Soc. 2008, 18, 438–443. [Google Scholar] [CrossRef]
- Feng, B.; Feng, Q.M.; Lu, Y.P. The effect of conditioning methods and chain length of xanthate on the flotation of a nickel ore. Miner. Eng. 2012, 39, 48–50. [Google Scholar] [CrossRef]
- Yu, Y.X.; Cheng, G.; Ma, L.Q.; Huang, G.; Wu, L.; Xu, H. Effect of agitation on the interaction of coal and kaolinite in flotation. Powder Technol. 2017, 313, 122–128. [Google Scholar] [CrossRef]
- Tabosa, E.; Rubio, J. Flotation of copper sulphides assisted by high intensity conditioning (HIC) and concentrate recirculation. Miner. Eng. 2010, 23, 1198–1206. [Google Scholar] [CrossRef]
- Feng, D.; Aldrch, C. Effect of preconditioning on the flotation of coal. Chem. Eng. Commun. 2005, 192, 972–983. [Google Scholar] [CrossRef]
- Pan, A.; Xie, M.H.; Li, C.; Xia, J.Y.; Chu, J.; Zhuang, Y.P. CFD Simulation of Average and Local Gas–Liquid Flow Properties in Stirred Tank Reactors with Multiple Rushton Impellers. J. Chem. Eng. Jpn. 2017, 50, 878–891. [Google Scholar] [CrossRef] [Green Version]
- Vlček, P.; Kysela, B.; Jirout, T.; Fořt, I. Large eddy simulation of a pitched blade impeller mixed vessel-comparison with LDA measurements. Chem. Eng. Res. Des. 2016, 108, 42–48. [Google Scholar] [CrossRef]
- Eggels, J.G. Direct and Large-eddy Simulation of Turbulent Fluid Flow Using the Lattice-Boltzmann Scheme. Int. J. Heat Fluid 1996, 17, 307–323. [Google Scholar] [CrossRef]
- Bakker, A.; Oshinowo, L.M. Modelling of turbulence in stirred vessels using large eddy simulation. Chem. Eng. Res. Des. 2004, 82, 1169–1178. [Google Scholar] [CrossRef]
- Zhou, G.; Kresta, S.M. Correlation of mean drop size and minimum drop size with the turbulence energy dissipation and the flow in an agitated tank. Chem. Eng. Sci. 1998, 53, 2063–2079. [Google Scholar] [CrossRef]
- Smoluchowski, M.V. Versuch einer mathematischen theorie der koagulations kinetis kolloider losungen. Z. Phys. Chem. 1918, 92, 129–168. [Google Scholar]
- Bakker, R.A. Micromixing in Chemical Reactors: Models, Experiments and Simulations. Ph.D. Thesis, TU Delft, Delft, The Netherlands, 1996. [Google Scholar]
- Yoon, H.S.; Balachandar, S.; Man, Y.H. Large eddy simulation of passive scalar transport in a stirred tank for different diffusivities. Int. J. Heat Mass Tran. 2015, 91, 885–897. [Google Scholar] [CrossRef]
- Zadghaffari, R.; Moghaddas, J.S.; Revstedt, J. Large-eddy Simulation of Turbulent Flow in a Stirred Tank Driven by a Rushton Turbine. Comput. Fluids. 2010, 39, 1183–1190. [Google Scholar] [CrossRef]
- Yeoh, S.L.; Papadakis, G.; Lee, K.C.; Yianneskis, M. Large Eddy Simulation of Turbulent Flow in a Rushton Impeller Stirred Reactor with Sliding-deforming Mesh Methodology. Chem. Eng. Technol. 2004, 27, 257–263. [Google Scholar] [CrossRef]
- Min, J.; Gao, Z.M. Large Eddy Simulations of Mixing Time in a Stirred Tank. Chinese J. Chem. Eng. 2006, 14, 1–7. [Google Scholar] [CrossRef]
- Derksen, J. Assessment of Large Eddy Simulations for Agitated Flows. Chem. Eng. Res. Des. 2001, 79, 824–830. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Wang, Y.; Yan, X.; Wang, A.; Cao, Y.A. Numerical study on efficient recovery of fine-grained minerals with vortex generators in pipe flow unit of a cyclonic-static micro bubble flotation column. Chem. Eng. Sci. 2017, 158, 304–313. [Google Scholar] [CrossRef]
- Wu, H.; Patterson, G.K. Laser-Doppler Measurements of Turbulent-flow Parameters in a Stirred Mixer. Chem. Eng. Sci. 1989, 44, 2207–2221. [Google Scholar] [CrossRef]
- Escudié, R. Structure de L’hydrodynamique Générée par une Turbine de Rushton. Ph.D. Thesis, INSA de Toulouse, Toulouse, France, 2001. (In French). [Google Scholar]
- Jaworski, Z.; Dyster, K.N.; Nienow, A.W. The effect of size, location and pumping direction of pitched blade turbine impellers on flow patterns: LDA measurements and CFD predictions. Chem. Eng. Res. Des. 2001, 79, 887–894. [Google Scholar] [CrossRef]
- Zadghaffari, R.; Moghaddas, J.S.; Revstedt, J. A Mixing Study in a Double-Rushton Stirred Tank. Comput. Chem. Eng. 2009, 33, 1240–1246. [Google Scholar] [CrossRef]
- Malik, S.; Lévêque, E.; Bouaifi, M.; Gamet, L.; Ghamri, N.; Simoëns, S.; El-Hajema, M. Shear improved smagorinsky model for large eddy simulation of flow in a stirred tank with a rushton disk turbine. Chem. Eng. Res. Des. 2016, 108, 69–80. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Yang, C.; Mao, Z. Large eddy simulation of liquid flow in a stirred tank with improved inner-outer iterative algorithm. Chinese J. Chem. Eng. 2006, 14, 47–55. [Google Scholar] [CrossRef]
- Soos, M.; Kaufmann, R.; Winteler, R.; Kroupa, M.; Lüthi, B. Determination of maximum turbulent energy dissipation rate generated by a rushton impeller through large eddy simulation. Aiche J. 2013, 59, 3642–3658. [Google Scholar] [CrossRef]
- Bakker, A.; Oshinowo, L.M.; Marshall, E.M. Chapter 31—The Use of Large Eddy Simulation to Study Stirred Vessel Hydrodynamics. In Proceedings of the 10th European Conference, Delft, The Netherlands, 2–5 July 2000; pp. 247–254. [Google Scholar]
- Escudié, R.; Bouyer, D.; Liné, A. Characterization of trailing vortices generated by a rushton turbine. Aiche J. 2004, 50, 75–86. [Google Scholar] [CrossRef]
- Derksen, J.; Akker, H. Large eddy simulations on the flow driven by a rushton turbine. Aiche J. 2010, 45, 209–221. [Google Scholar] [CrossRef]
- Deglon, D.; Meyer, C. CFD modeling of stirred tanks: Numerical considerations. Miner. Eng. 2006, 19, 1059–1068. [Google Scholar] [CrossRef]
- Bartels, C.; Breuer, M.; Wechsler, K.; Durst, F. Computational fluid dynamics applications on parallel-vector computers: computations of stirred vessel flows. Comput. Fluids. 2002, 31, 69–97. [Google Scholar] [CrossRef]
- Hudcova, V.; Machon, V.; Nienow, A.W. Gas-liquid dispersion with dual Rushton turbine impellers. Biotechnol. Bioeng. 1989, 34, 617–628. [Google Scholar] [CrossRef] [PubMed]
- Taghavi, M.; Zadghaffari, R.; Moghaddas, J.; Moghaddas, Y. Experimental and cfd investigation of power consumption in a dual rushton turbine stirred tank. Chem. Eng. Res. Des. 2011, 89, 280–290. [Google Scholar] [CrossRef]
- Escudié, R.; Liné, A. A simplified procedure to identify trailing vortices generated by a rushton turbine. Aiche J. 2010, 53, 523–526. [Google Scholar] [CrossRef]
- Escudié, R.; Liné, A. Experimental analysis of hydrodynamics in a radially agitated tank. Aiche J. 2003, 49, 585–603. [Google Scholar] [CrossRef]
- Yeoh, S.L.; Papadakis, G.; Yianneskis, M. Numerical simulation of turbulent flow characteristics in a stirred vessel using the les and rans approaches with the sliding/deforming mesh methodology. Chem. Eng. Res. Des. 2004, 82, 834–848. [Google Scholar] [CrossRef]
- Dey, S. Enhancement in hydrophobicity of low rank coal by surfactants-a critical overview. Fuel Process. Technol. 2012, 94, 151–158. [Google Scholar] [CrossRef]
- Peng, Y.; Liang, L.; Tan, J.; Sha, J.; Xie, G. Effect of flotation reagent adsorption by different ultra-fine coal particles on coal flotation. Int. J. Miner. Process. 2015, 142, 17–21. [Google Scholar] [CrossRef]
- Xia, W.; Yang, J.; Liang, C. A short review of improvement in flotation of low rank/oxidized coals by pretreatments. Powder Technol. 2013, 237, 1–8. [Google Scholar] [CrossRef]
- Zhou, F.; Yan, C.; Wang, H.Q.; Zhou, S.; Liang, H. The result of surfactants on froth flotation of unburned carbon from coal fly ash. Fuel 2017, 190, 182–188. [Google Scholar] [CrossRef]
- Deglon, D.A. The effect of agitation on the flotation of platinum ores. Miner. Eng. 2005, 18, 839–844. [Google Scholar] [CrossRef]
- Hower, J.C.; Groppo, J.G.; Graham, U.M.; Wardb, C.R.; Kostovac, I.J.; Maroto-Valer, M.M.; Dai, S.F. Coal-derived unburned carbons in fly ash: A review. Int. J. Coal Geol. 2017, 179, 11–27. [Google Scholar] [CrossRef]











| Region | Flow in (L/s) | Flow out (L/s) | Difference (%) |
|---|---|---|---|
| 0 ≤ r ≤ 55 mm | 0.3683 | 0.3735 | 1.4 |
| 55 ≤ r ≤ 85 mm | 0.7474 | 0.7422 | 0.7 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Zhu, Z.; Qi, X.; Yan, X.; Zhang, H. The Process of the Intensification of Coal Fly Ash Flotation Using a Stirred Tank. Minerals 2018, 8, 597. https://doi.org/10.3390/min8120597
Yang L, Zhu Z, Qi X, Yan X, Zhang H. The Process of the Intensification of Coal Fly Ash Flotation Using a Stirred Tank. Minerals. 2018; 8(12):597. https://doi.org/10.3390/min8120597
Chicago/Turabian StyleYang, Lu, Zhenna Zhu, Xin Qi, Xiaokang Yan, and Haijun Zhang. 2018. "The Process of the Intensification of Coal Fly Ash Flotation Using a Stirred Tank" Minerals 8, no. 12: 597. https://doi.org/10.3390/min8120597
APA StyleYang, L., Zhu, Z., Qi, X., Yan, X., & Zhang, H. (2018). The Process of the Intensification of Coal Fly Ash Flotation Using a Stirred Tank. Minerals, 8(12), 597. https://doi.org/10.3390/min8120597