Next Article in Journal
Serpentine–Hisingerite Solid Solution in Altered Ferroan Peridotite and Olivine Gabbro
Next Article in Special Issue
Design of Flotation Circuits Using Tabu-Search Algorithms: Multispecies, Equipment Design, and Profitability Parameters
Previous Article in Journal
Basin Evolution and Massive Sulfide Deposition at Rammelsberg (Germany): Updating the Subsidence Analysis
Previous Article in Special Issue
Optimizing Flotation Circuit Recovery by Effective Stage Arrangements: A Case Study
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Minerals
Volume 9
Issue 1
10.3390/min9010046
minerals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Study of K-Feldspar and Lime Hydrothermal Reaction: Phase and Mechanism with Reaction Temperature and Increasing Ca/Si Ratio

by
Shanke Liu
1,2,*,
Cheng Han
1,2 and
Jianming Liu
1,2
1
Key Laboratory of Mineral Resources, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China
2
Institutions of Earth Science, Chinese Academy of Sciences, Beijing 100029, China
*
Author to whom correspondence should be addressed.
Minerals 2019, 9(1), 46; https://doi.org/10.3390/min9010046
Submission received: 15 December 2018 / Revised: 30 December 2018 / Accepted: 9 January 2019 / Published: 14 January 2019
(This article belongs to the Special Issue Modeling, Design and Optimization of Multiphase Systems in Minerals Processing)
Browse Figures
Review Reports Versions Notes

Abstract

:
To elucidate the physicochemical properties of the artificial silicate composite material, K-feldspar and lime were reacted in mild hydrothermal conditions (different reaction temperatures and various K-feldspar/lime ratios). Formed phases were investigated using various techniques, such as X-ray powder diffraction, the Rietveld method, scanning electron microscopy (SEM), and inductively coupled plasma-optical emission spectrometry. The analysis revealed that tobermorite, grossular (hydrogarnet), alpha-dicalcium silicate hydrate (α-C2SH), amorphous calcium silicate hydrate, potassium carbonate, bütschliite, calcite, and calcium hydroxide formed with various conditions. Both the temperature and the Ca/Si molar ratio in the starting material greatly affected the formation of phases, especially the generation of tobermorite and α-C2SH. The substitution of H4O4 ↔ SiO4 proceeded with the increase of the Ca/Si molar ratio rather than the reaction temperature and the reaction time. More hydrogen was incorporated in hydrogarnet through the substitution of H4O4 ↔ SiO4 with the increase of the Ca/Si molar ratio in the starting material. Due to the properties of tobermorite as a cation exchanger and its potential applications in hazardous waste disposal, experimental parameters should be optimized to obtain better performance of the artificial silicate composite material from K-feldspar and lime hydrothermal reaction. The dissolution mechanism of K-feldspar was also discussed.

Graphical Abstract

1. Introduction

Silicates are extremely important materials, both naturally and artificially, for the development of science and technology. Although there is no known way of accurately ascertaining the abundance of every mineral within the earth’s crust, based on a rough estimate, silicates comprise most of the earth’s crust, as shown in Figure 1 [1]. In addition, silicates are the main component of ceramics, Portland cement, and glass. Silicate-based materials as amendments such as zeolites, clays, and cementitious materials show increasing interest in the stabilization/solidification of heavy-metal contaminated soils or environments [2,3,4].
Recently, an artificial silicate composite material, namely a nanosubmicron mineral-based soil conditioner (NMSC) prepared by the hydrothermal reaction of K-feldspar and lime, was reported [5,6,7]. Field and in-house tests indicated that the artificial silicate composite material showed excellent performance and served multiple functions that were closely related to its physicochemical properties and mineral components [8,9]. Of them, both carbonates and 11 Å tobermorite contributed to pH improvement and the inhibition of cadmium (Cd) uptake in rice. Tobermorite is one of the calcium silicate hydrate (CSH) compounds, and the main interest is related to its close relationship with the CSH phases formed during the hydration of Portland cement [10]. In addition, tobermorite may act as cation exchangers to absorb unhealthy elements and has potential applications in waste disposal [11,12,13]. Tobermorite is also a slow-release reservoir for some nutrients, such as [K+] and [NH4+] [14]. As a primary product of the hydrothermal reaction, the weight percentage of tobermorite can reach 35%–40% by controlling the reaction conditions.
In a CaO–Al2O3–SiO2–H2O (C–A–S–H) hydrothermal system, the abundance of formed minerals is closely related to the reaction conditions, such as the ratio of starting reactants [15,16,17]. Therefore, a study of mineral components and its abundance is a key point for the artificial silicate composite material under the different reaction conditions. We carried out a primary test on the hydrothermal reaction of K-feldspar and lime by a single-factor analysis [18]. However, at that time, the authors did not realize that the silicate composite material NMSC would show such excellent performance and serve multiple functions, as mentioned above [8,9]. Therefore, the main aim of the previous test was to improve the percentage of K-feldspar dissolution via optimizing experimental parameters. We further investigated the mechanism of the hydrothermal reaction between K-feldspar and different alkalis [including Ca(OH)2] and identified minerals formed through an elaborative interface experiment [19]. Several researchers also studied the preparation of potassium fertilizer via the hydrothermal alternation of K-feldspar ore at 200 °C [20,21]. However, none of the abovementioned studies investigated the hydrothermal reaction of K-feldspar under alkaline conditions with reaction conditions, such as various reaction temperatures, various reactant ratios (the ratio of K-feldspar and lime in the starting material), and various reaction times. For a better understanding of the chemistry and mineralogy of the artificial silicate composite material, the investigation of K-feldspar and lime hydrothermal reaction must consider various conditions rather than a limited one.
Three groups of the hydrothermal experiments were carried out for investigating the K-feldspar and lime system with various conditions, i.e., the reaction temperature, the reactant ratio, and the reaction time. For each group of the hydrothermal experiment, only one factor was changed and others remained constant. The reaction temperatures of 130 °C to 250 °C were chosen for studying the effects of the reaction temperature on the hydrothermal reaction between K-feldspar and lime. In general, the operating temperature of a common autoclave in China is approximately 190 °C in order to ensure safety during the production. Therefore, based on a view from the commercialization point, the reaction temperature of 190 °C was chosen for studying the hydrothermal reaction with the reaction time (from 0 h to 36 h) and the reactant ratio (the ratio of K-feldspar and lime was 3:7 to 7:3, and 10 g total solid mixture was fixed). The artificial silicate composite material under various hydrothermal conditions was systematically investigated by combining various techniques, such as X-ray powder diffraction (XRPD), the Rietveld method, scanning electron microscopy (SEM), energy dispersive X-ray spectroscopy (EDS), and inductively coupled plasma–optical emission spectrometry (ICP–OES). The material was then further analyzed from a viewpoint of chemistry and mineralogy. We published the report of the hydrothermal reaction with the reaction time in another journal [22]. Here, we only present the results of the hydrothermal reaction with the reaction temperature and the reactant ratio.

2. Materials and Methods

Materials and methods were briefly described in the publication of Liu et al. [18] and are stated in detail here for better understanding.

2.1. Materials

K-feldspar was obtained from a quarry near Geshi Town, Ningyang County, Shandong Province, China, and its chemical formula is (K0.96Na0.04)(Al1.00Si3.00)O8.00. Lime (CaO, AR) was obtained from Sinopharm Chemical Reagent Co., Ltd. (Beijing, China).

2.2. Hydrothermal Method

K-feldspar blocks were crushed using a jaw crusher and then pulverized by a Vibratory Disc Mill RS 200 (Retsch, Hann, Germany). Lime blocks were manually crushed and ground in an agate mortar. Both materials were sieved to a particle size of less than 74 µm by a 200-mesh screen.

2.2.1. Reaction Temperature

A mixture of K-feldspar powder (5.5 g), lime powder (4.5 g), and deionized water (30 mL) was homogenously blended for five minutes by a magnetic agitator at the speed of 500 rpm, and then was heated in an autoclave (100 mL volume) for 20 h at 130, 160, 190, 220, and 250 °C. After the hydrothermal reaction ended, the reactors were naturally cooled to room temperature. For comparison, the same operation was carried out for a mixture of 5.5 g K-feldspar powder, 4.5 g lime powder, and 30 mL deionized water in an autoclave at room temperature (25 °C). Then, the production materials were removed from the autoclaves and dried at 105 °C for 12 h. Finally, the samples were manually crushed and ground in an agate mortar to prepare them for assessment. These corresponding production materials at 25, 130, 160, 190, 220, and 250 °C were labeled as L–1, L–2, L–3, L–4, L–5, and L–6, respectively.

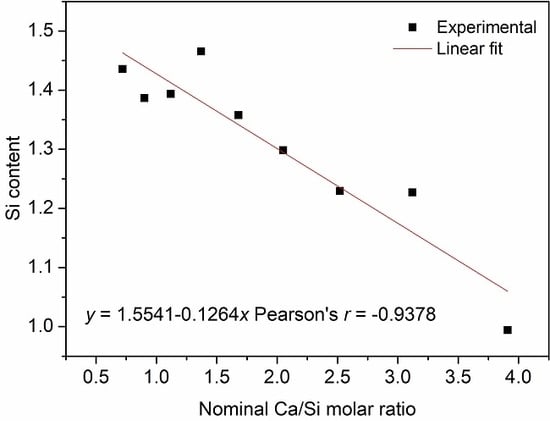
2.2.2. Reactant Ratio

A 10 g solid powder mixture of K-feldspar and lime was cooked along with 30 mL deionized water in the autoclaves at 190 °C for 13.6 h. The mixture was obtained by homogeneously blending K-feldspar powder and lime powder in dry conditions, and K-feldspar/lime mass ratio in the mixture was 7/3, 6.5/3.5, 6/4, 5.5/4.5, 5/5, 4.5/5.5, 4/6, 3.5/6.5, and 3/7, respectively. After the hydrothermal reaction was stopped, the reactors were naturally cooled to room temperature. Then, the productions were removed from those autoclaves and were dried at 105 °C for 12 h. Lastly, they were crushed and ground for evaluation. The hydrothermal productions for various K-feldspar/lime mass ratios of 7/3, 6.5/3.5, 6/4, 5.5/4.5, 5/5, 4.5/5.5, 4/6, 3.5/6.5, and 3/7 were labeled as M–1, M–2, M–3, M–4, M–5, M–6, M–7, M–8, and M–9, respectively (Table S1).

2.3. Leaching Experiment

To analyze the chemical composition, a 1-g aliquot of each sample (fifteen samples, from L–1 to L–6 and from M–1 to M–9) was added to 100 ml of deionized water, and another 1-g aliquot was added to 100 ml of 0.5 mol·L−1 HCl. Both samples were placed in a constant-temperature oscillator for one hour and filtered through filter paper. The filtered solutions and residues were conserved for further analysis.

2.4. Analytical Methods

2.4.1. SEM and EDS

The morphology of the powdered materials was studied using a Leo 1450 VP SEM instrument (Carl Zeiss AG, Jena, Germany) under high vacuum on the uncoated specimen, operated at 20 kV and with a beam current of 1 nA. EDS using an energy dispersive X-ray spectrometer (mounted on the scanning electron microscope, Kevex superdry EDS, Valencia, CA, USA) was performed to measure an average composition of spherical and bar particles of Sample L–6. The H atom was not provided by EDS because of the limited resolution.

2.4.2. XRPD

To distinguish the phases formed during the hydrothermal reactions, XRPD patterns of all of the powdered samples (fifteen samples, L–1 to L–6 and M–1 to M–9) were obtained using a Dmax2400 X-ray diffractometer (Rigaku, Tokyo, Japan) at 40 kV and 80 mA in the 2 theta range from 3° to 65° at a step of 0.02° with a counting time of 0.3 s per step and a total scan time of 15 min 30 s. Quantitative phase analysis (QPA) of the XRPD results was conducted using GSAS [23] and EXPGUI [24] software with the Rietveld method [25]. The instrumental parameter file was obtained from the XRPD pattern of LaB6 standard (SRM 660b, National Institute of Standards and Technology, USA).

2.4.3. ICP-OES

The element concentrations in the filtrated solutions were determined using ICP–OES with IRIS advantage inductively coupled argon plasma optical emission spectrometers (Thermo Fisher Scientific Inc., Waltham, MA, USA), and its limit of detection (LOD) was 3σ (σ is the standard deviation of blank determination), and the relative standard deviation (RSD) was approximately 0.5%–2.0%.

3. Results and Discussion

In an early study [18], the authors performed the hydrothermal reaction using the same process as that mentioned in the experimental section. Samples of L–1 to L–6 and samples of M–1 to M–9 in this work corresponded to from LSF12–1 to LSF12–6 and from LSF11–1 to LSF11–9, respectively, in a previous work [18]. In that report, we aimed to optimize the experimental parameters by the single-factor analysis in order to improve the percentage of K-feldspar dissolution. Therefore, we have not presented the results reported in that paper yet. Here, we only show new analysis and supply additional data to better understand the physicochemical properties of K-feldspar and lime hydrothermal reactions.

3.1. Phase

3.1.1. Crystal

With the reaction temperature and the reactant ratio (the Ca/Si molar ratio), the hydrothermal treatment of K-feldspar with lime exhibited complex product phases, including remaining K-feldspar, calcium hydroxide, calcite, grossular, tobermorite, alpha-dicalcium silicate hydrate (α-C2SH), potassium carbonate, bütschliite, and amorphous calcium silicate hydrate (ACSH) (Figure 2, Table 1 and Table S2). In fact, the products were finally formed through a two-step process (Figure S1). First, calcium (alumino) silicate hydrates and potassium or calcium hydroxide were produced in the pressure-tight autoclaves during heating. Then, carbonates were formed through the reaction between their corresponding hydroxides and carbon dioxide during the drying of the sample at 105 °C in air.
With the increase of the reaction temperature, the amount of K-feldspar decreased in terms of the quantitative phase analysis data (Figure 2 and Table S2). However, K-feldspar were still discernible when the temperature was increased to 250 °C, which suggests that the K-feldspar structure is difficult to destroy under these hydrothermal conditions. All calcium hydroxide apparently reacted when the temperature reached 190 °C (Table S2). With the increasing of the Ca/Si ratio, calcium hydroxide appeared when the Ca/Si ratio reached 1.68, indicating that calcium hydroxide was apparently leftover. More and more calcium hydroxide was formed. The QPA results demonstrated that the amount of leftover K-feldspar decreased with the increasing Ca/Si molar ratio (Figure 2 and Table S2), and this was in accord with its decreasing ratio in the starting material. However, there still left about 13% K-feldspar when the Ca/Si ratio reached 3.91 (the weight ratio between K-feldspar and lime is 3:7), and approximately 60% K-feldspar reacted with lime in terms of an estimation. K-feldspar did not react with lime at room temperature (25 °C) because only calcium hydroxide and calcite were formed for L-1 while the sample was dried at 105 °C in air (Table S2). In fact, all carbonates were formed while the sample was dried at 105 °C in air. Calcite appeared in all the produced materials (Table 1). With the exception of potassium carbonate, the double carbonate bütschliite began to appear. Bütschliite can be obtained in the systems of CaCO3—K2CO3–H2O and CaCO3/Ca(OH)2–KOH–H2O at room temperature [26,27]. This was proven by the fact that bütschliite, calcium hydroxide, and calcite were identified as the phases contained in the solid residue. The solid residue was obtained by vaporing a mixed solution filtrated from a mixture of a 1-g aliquot of each sample (nine samples, M–1 to M–9) and 100 ml of deionized water (Figure S2). Therefore, potassium hydroxide, which was not detected by XRPD, reacted with calcium hydroxide and carbon dioxide to form bütschliite during the drying of the sample at 105 °C in air.
Three crystal calcium aluminosilicate hydrates, i.e., grossular (hydrogarnet), α-C2SH, and tobermorite, were formed under the set hydrothermal conditions (Figure 2, Table 1 and Table S2). Higher contents of grossular and tobermorite generated at higher temperatures. Grossular stably existed after its appearance. However, the generation of α-C2SH and tobermorite was greatly affected by the reaction condition. For example, with the increase in temperature, α-C2SH only appeared at 190 °C, and tobermorite existed from 190 °C to 250 °C. With the increase of the Ca/Si ratio, α-C2SH stably existed after its appearance when the Ca/Si ratio reached 1.37. However, tobermorite disappeared when the Ca/Si ratio reached 1.68.
The K-feldspar–lime hydrothermal system is composed of K2O–CaO–Al2O3–SiO2–H2O, i.e., K–C–A–S–H, which has the same elements as those of CaO–Al2O3–SiO2–H2O (C–A–S–H) except K. However, the minerals of tobermorite, α-C2SH, and hydrogarnet are common phases for both systems [15,16,17,28,29,30,31,32]. Taylor summarized the phase stability of the CaO–SiO2–H2O (C–S–H) system: 11 Å tobermorite stably exists below 200 °C, and α-C2SH exists below 150 °C [16,17]. Meller et al. [16] determined that the phase stability was radically altered by small quantities of additives. In their study, as the upper temperature limits of α-C2SH (<250 °C) and 11 Å tobermorite (<300 °C) increased, hydrogarnet was the only aluminum-bearing phase that was stable below 300 °C, and the presence of alumina greatly increased the stability of 11 Å tobermorite. In this study, tobermorite was stable from 190 °C to 250 °C, grossular was stable from 160 °C to 250 °C, and α-C2SH appeared only at 190 °C. These results are consistent with the results obtained in the studies by Ríos et al. and Meller et al. [15,16]. There was no evidence that Al-substituted tobermorite was formed; however, it is possible that the Al substitution for Si in tobermorite increased its stability [33,34]. Besides, the generation of α-C2SH and tobermorite was greatly affected by the initial Ca/Si ratio in the starting material (Table 1). Here, the analysis shows that grossular was generated prior to α-C2SH and tobermorite with an increase in the reaction temperature, revealing that it is easier to generate grossular than α-C2SH and tobermorite under the hydrothermal conditions. Since the Ca atoms of grossular, α-C2SH, and tobermorite originate from lime, both Si and Al originate from K-feldspar. Therefore, there is no competition of parallel reactions. The phase transformation is also true for α-C2SH because α-C2SH appeared at 190 °C and disappeared at 220 °C, showing that α-C2SH is metastable and transforms to a more stable phase at higher temperatures [17,35].
As a layered silicate, tobermorite has high exchangeability and selectivity for cations [11], which can alleviate the damage of heavy metals such as Cd, Pb, and Cr on soil [13,36,37]. Tobermorite is also a slow-release reservoir for some nutrients, such as [K+] and [NH4+] [14]. As a primary product of the hydrothermal reaction, the weight percentage of tobermorite can reach 35%–40% by controlling the reaction conditions (Table S2). Tobermorite has a structure similar to that of the 2:1 clay minerals, and this structure plays a key role in the soil K cycle [38] with a positive correlation to the pH buffering capacity [39,40], thereby benefitting the soil.
The general formula of 11 Å tobermorite may be written as Ca4+x(AlySi6-y)O15+2x-y(OH)2−2x+y·5H2O, with 0 ≤ x ≤ 1 and 0 ≤ y ≤ 1. The variable x represents the amount of additional calcium hosted in the structural cavities. Consequently, 11 Å tobermorite is actually a series between two endmembers, Ca4Si6O15(OH)2·5H2O and Ca5Si6O17·5H2O [41]. Therefore, the Ca/Si ratio in the structure of tobermorite is [0.67, 0.83]. Based on a magnified view of XRPD, the CSH gel phase—rather than tobermorite—was formed when the Ca/Si ratio deviated from an ideal one in the structure of tobermorite (the star phase in Figure S3). Wang et al. [42] found that the deviation of the Ca/Si molar ratio from 0.8 to 1.4 impeded the appearance of tobermorite, and this conclusion is in accord with the trend of the tobermorite appearance with the Ca/Si ratio. However, with the increasing of the Ca/Si ratio, it seemed beneficial for the formation of α-C2SH due to its high Ca/Si ratio. It is well known that Al-substituted tobermorite will lead an increase of the basal spacing (002) between the silicate layers along the c axis and the basal spacing increases with Al content [33,43,44]. Compared to tobermorite synthesized without Al, the (002) diffraction peak of samples from L–4 to L–6, from M–1 to M–4, and from Tm–6 to Tm–10 shifted towards lower angles (Figure 3). The content of Al for Si substitution should have been similar because two theta angles of the (002) diffraction peaks of all these samples were almost the same. Considering that the Al/Si ratio was constant due to their shared source from K-feldspar, the conclusion seems reasonable. The EDS data showed that tobermorite contained K and Al atoms. Therefore, we concluded that Al-substituted tobermorite was formed (Table S6).
The hydrogarnet is an important mineral that is often found in nature and hydrated cement. A calcic hydrogarnet that occurs frequently in the literature is hydrogrossular, Ca3Al2(SiO4)3−x(OH)4x (0 ≤ x ≤ 3), and has intermediate compositions between grossular (x = 0) and katoite (x = 3). The structure of hydrogarnet (cubic, space group I a 3 ¯ d , no. 230) consists of AlO6 octahedra and SiO4 tetrahedra linked with oxygen and the hydroxyl component (OH) in a solid solution with both (OH) and (SiO4) units depending on the composition x [45,46]. A linear relationship between lattice parameter a and x or a and Si content was observed for natural and artificial hydrogarnet [32,47,48], and a good agreement of the Si content estimates from XRD and EPMA was proven [32]. By plotting Si content (3 − x) against lattice parameter a from the powder diffraction file (PDF) data, a linear equation was obtained for hydrogarnet (Figure 4a):
3 − x = 48.4521 − 3.8529 a
The Si content of grossular in the samples of M–1 to M–9 was calculated from Equation (1) and was plotted against the Ca/Si ratio in the starting material in Figure 4b. These values of Si content calculated from Equation (1) basically agreed with those obtained in terms of Figure 3 from Kyritsis et al. [32], Figure 1A from Okoronkwo and Glasser [48], and Figure 2 from Adhikari et al. [49]. It is observed from Figure 4b that more hydrogen was incorporated in hydrogarnet through H4O4 ↔ SiO4 with an increase of the Ca/Si molar ratio in the starting material (nominal Ca/Si molar ratio), which is basically consistent with the conclusion of the references [16,32]. Particularly, more hydrogen incorporation proceeded after calcium hydroxide appeared at NCa/Si = 1.68, which agreed with the shift of XRPD towards a lower angle for samples from M–5 to M–9 (a magnified view of the characteristic diffraction peak (420) of hydrogarent in Figure 5b). However, the ratio of H4O4 ↔ SiO4 in hydrogarnet seemed to remain constant due to the same position of the diffraction peak (420) of hydrogarent for the samples of L–2 to L–6 and of Tm–3 to Tm–10. This indicated that neither the reaction temperature nor the reaction time affected the substitution of H4O4 ↔ SiO4 in hydrogarnet if there was the same Ca/Si molar ratio in the starting material.
In order to obtain one single phase, some researchers used the responding oxides to prepare tobermorite and hydrogarnet. For example, tobermorite was synthesized from lime and quartz or lime and fumed silica powder under the hydrothermal condition with the designed Ca/Si molar ratio (0.83) according to the ideal composition of tobermorite (Ca5Si6O16(OH)2·4H2O) [13,33,44,50]. Hydrogarnet was synthesized through silica gel, calcium hydroxide, and γ-alumina [51]. Therefore, the generation of the abovementioned phases was closely related to the atom ratio rather than the sources of Ca, Si, and Al in the starting materials. In this study, Ca was from lime, and Al and Si were both from K-feldspar. In terms of estimated Si content, the Al/Si ratio in hydrogarnet was [1.39, 2.01], which was greater than the ratio of 1:3 in the K-feldspar structure. When one structural unit of K-feldspar was destroyed by Ca2+ and OH− attacking, K+ was leached into the solution [19]. Released Al and Si combined with Ca to form hydrogarnet, and residual Si reacted with Ca to form crystal or ACSH. Al of K-feldspar mainly entered into the structure of hydrogarnet, and Si distributed in both hydrogarnet and caclium silicate hydrates.

3.1.2. Amorphous

With an increase in the reaction temperature and the Ca/Si ratio, the ACSH diffraction peak was verified by a slight bump at 29° for M–5 to M–9 (* phase in Figure S3) and L–2 to L–3 (* phase in Figure S4). This was also true for the samples of Tm–3 to Tm–5 with a time increase [22]. In fact, the bump corresponded to a diffraction peak of CSH gel and became a stronger diffraction peak of tobermorite when the CSH gel was transformed into tobermorite [52,53,54,55]. CSH gel is the principal hydration product and primary binding phase in C–A–S–H or C–S–H systems such as Portland cement. It is generally accepted that the CSH gel phase has a tobermorite-like structure, which can be described as a layer of CaO polyhedra sandwiched between individual silicate chains that are organized in a “dreierketten” structure [10,56]. Some researchers confirmed that lime and Si-containing phases, such as quartz or cement, produced CSH gel with relatively low crystallinity during the hydrothermal reaction and then formed tobermorite with higher crystallinity [57,58]. Shaw et al. employed in situ energy-dispersive X-ray diffraction techniques to study the hydrothermal formation of crystalline tobermorite from 190 °C to 310 °C [57]. First, a poorly crystalline CSH gel phase was formed. The second stage involved the ordering of the CSH gel to form ordered crystalline tobermorite. Based on the phase analysis, ACSH existed in all samples (Table S2). K-feldspar was the only residual after the product was filtrated by 0.5 mol·L−1 HCl. Therefore, these amorphous phases should have been acid soluble [22]. All formed phases were concluded to be calcium silicate hydrate or calcium aluminosilicate hydrate by EDS analysis, and the amorphous phases were mainly composed of calcium silicate hydrates or some transition state compounds that were discussed in a previous work [19]. Here, ACSH may have contained other amorphous phases—except calcium silicate hydrates—and all of these phases were judged to be amorphous by XRPD [20]. Therefore, the authors did not further determine the chemical compositions of ACSH because it was still difficult to distinguish different crystal or amorphous phases, even using Electron Probe Micro-Analyzer (EPMA) due to small particles and quantities of intertwining phases [19,20].

3.2. Morphology

Considering the complexity of the products and the inability to identify the phases of different morphology, we do not discuss the SEM images of the samples of M–1 to M–9 and only present the SEM images of the starting materials K-feldspar and lime (Figure 6) and the samples of L–1 to L–6 (Figure 7).
Figure 6 shows that the unreacted K-feldspar powder consisted of a few to tens of micron-sized particles and that lime was composed of a few micron-sized particles, which were obviously prepared from a calcining material. When K-feldspar and lime were kept under a closed hydrothermal reactor for 13.6 h at room temperature, no reaction occurred. However, lime reacted with water to form calcium hydroxide and further carbonized to form calcite during the drying of the sample at 105 °C in air. Figure 7a clearly shows that several floccules adhered to the K-feldspar surface, and these floccules were identified as calcium hydroxide and calcite based on the XRPD results (Table S2). The morphology of the hydrothermal product L–2 was different from that of L–1. Large quantities of floccules were deposited on the surface of the K-feldspar particle, and several spherical particles appeared (Figure 7b). When the temperature was increased to 160 °C, many squamiform slices appeared on the K-feldspar particles, and these slices may have been calcium hydroxide, calcite, and potassium carbonate (Figure 7c). At 190 °C, the products were diverse, and it was difficult to distinguish the phases by their different morphologies (Figure 7d). At higher temperatures, the amount of spherical and laminar particles increased, which was in accordance with the QPA results demonstrating that more grossular and tobermorite were formed (Figure 7e,f). The chemical compositions of the laminar and spherical particles were determined using EDS (Figure 8 and Table S6). The Ca/Al and Ca/(Al + Si) atom ratios determined by EDS were 1.63 and 0.62 for the spherical particle (Figure 8a), respectively, and approached the corresponding ratio values of grossular [NCa/Al = 1.5 NCa/(Al+Si) = 0.85, Ca3Al2(SiO4)1.53(OH)5.88, PDF card number 01-075-1690]. The Ca/Si atom ratio determined by EDS was 0.72 for the laminar particle (Figure 8b) and approached its corresponding ratio value of tobermorite [NCa/Si = 0.75, Ca2.25(Si3O7.5(OH)1.5)(H2O), PDF card number 01-083-1520]. The spherical particle contained a K atom and the laminar one contained both K and Al atoms, and this may have been caused by the intertwining of the formed phases with each other. As a result, the ratio determined by EDS slightly deviated from the reference value. Therefore, in this study, the laminar phase was tobermorite, as identified in our previous study and by other researchers [19,59,60,61,62], and the spherical particle was grossular, as identified in our previous study and by other researchers [19,60,63].

3.3. Dissolution Mechanism

For investigating the dissolution mechanism of K-feldspar under hydrothermal condition, we analyzed the percentage of K-feldspar dissolution (Table S7, and the percentage of K-feldspar dissolution was calculated from their corresponding element contents in Table S3; please see the Supplementary Materials) with the reaction temperature. Because K-feldspar did not react with lime at room temperature (25 °C), the authors did not consider the data of K-feldspar dissolution at this temperature. Only five-point data were fitted between the natural logarithm of the dissolution percentage (lnD) and the reciprocal of the temperature (1/T, K−1). When lnD versus 1/T (K−1) was plotted in Figure 9, a turning point was found rather than a linear relationship. As a result, the plot of lnD vs. 1/T could be divided into two regions: I, [130 °C, 190 °C], and II, [190 °C, 250 °C]. Then, two fitted lines were applied to these two regions:
I :   l n D = 13.4850 − 4346.3643 T   ( 403 K ≤ T ≤ 463 K ;   Pearson’s   r = − 0.9914 )
II :   l n D = 7.6155 − 1593.4882 T   ( 463 K ≤ T ≤ 523 K ;   Pearson’s   r = − 0.9843 ) .
In terms of the Arrhenius equation, the following represents the relationship between lnD and the dissolution apparent activation energy Ea:
l n D = l n A − E a / R T .
When Equation (4) was differentiated, the following equation was obtained:
E a = − R d l n D d ( 1 T ) .
Based on Equation (5), the activation energies were calculated as 36 kJ/mol at 130 °C ≤ T ≤ 190 °C and 13 kJ/mol at 190 °C ≤ T ≤ 250 °C.
In general, Ea is a constant over a small temperature range, which is true for regions I and II in Figure 9. Using a similar hydrothermal condition at higher temperatures (260–290 °C), Liu et al. [64] found a linear relationship between lnK and 1/T and calculated the activation energy for the K-feldspar and slaked lime hydrothermal reaction. However, the activation energy calculated by those authors was 23 kJ/mol, which was larger than 13 kJ/mol at 190 °C ≤ T ≤ 250 °C and less than 36 kJ/mol at 130 °C ≤ T ≤ 190 °C in this work. It is reasonable to assume that different experimental conditions or approaches can cause a difference in the activation energy calculations [65].
From the activation energy data, we concluded that two different processes controlled the reaction, and a sketch of these processes is illustrated in Figure 10. First, the reaction was controlled by a dissolution-precipitation process (region I). At higher temperatures, the reaction was dominated by a diffusion process due to the quantities of deposited phases (region II). A similar trend was also found for the dissolution of K-feldspar with the reaction time. Through a preliminary interface study, Liu et al. [19] concluded that the reaction between K-feldspar and lime under hydrothermal conditions was a mineral-mineral replacement reaction proceeded by the dissolution-precipitation mechanism. The dissolution-precipitation mechanism was true for a reaction that occurs on the K-feldspar particle surface at medium temperatures, i.e., 160–190 °C. Under this condition, the rate of K-feldspar dissolution was close to the deposition rate of the formed phases. However, at higher temperatures, due to the deposition of large quantities of mineral phases on the K-feldspar surface, the diffusion of K+ and Ca2+ was blocked. The mechanism in Figure 10 is consistent with the SEM results (Figure 7) because more phases were deposited on the K-feldspar surface at higher temperature.
By studying the kinetics and mechanism of the hydrothermal synthesis of barium titanate, Eckert et al. found that multiple reaction mechanisms competed in different regimes [66]. Berger et al. measured the rate of mineral dissolution of sanidine from 100 °C to 300 °C and suggested a competition between two parallel reactions at the mineral surface [67]. In this work, different reaction mechanisms dominated in various temperature regions, which is in agreement with the abovementioned conclusions.

4. Conclusions

Based on an environmentally friendly hydrothermal process, the artificial silicate composite material generated from natural silicate rock, i.e., K-feldspar, exhibited complex mineralogical properties. Except carbonates (namely, potassium carbonate, calcite, and bütschliite), calcium (alumno) silicates—including grossular, tobermorite, alpha-dicalcium silicate hydrate, and amorphous calcium silicate hydrate—were the main products of the K-feldspar and lime hydrothermal reaction in the 130 °C to 250 °C temperature range and in the 7:3 to 3:7 K-feldspar/lime weight ratio range (i.e., the Ca/Si molar ratio from 0.72 to 3.91). Both the temperature and the Ca/Si molar ratio in the starting material greatly affected the formation of phases, especially the generation of tobermorite and α-C2SH. The substitution of H4O4 ↔ SiO4 proceeded with the increase of the Ca/Si molar ratio rather than the reaction temperature and the reaction time. More hydrogen was incorporated in hydrogarnet through the substitution of H4O4 ↔ SiO4 with the increase of the Ca/Si molar ratio in the starting material.
The dissolution mechanism analysis showed that a turning point between the natural logarithm of the percentage of K-feldspar dissolution and the reciprocal of the temperature (K−1) appeared, implying that different reaction mechanisms controlled K-feldspar dissolution. The apparent activation energies were also calculated.
Based on the results of phase analysis and from a point of environmental and economic views, the mass ratio of K-feldspar and lime should be more than 55:45 to obtain optimized properties of synthesized silicate composite material. More lime in the starting materials means higher product cost due to the higher price compared with K-feldspar. However, because of the properties of tobermorite as a cation exchanger and its potential applications in hazardous waste disposal, experimental parameters should be optimized to obtain better performance of the artificial silicate composite material from the K-feldspar and lime hydrothermal system. A detailed study is worthy of being carried out for investigating the relationship between the mineralogy and the function of the artificial silicate composite material.
As a potential sustainable agromineral, the artificial composite silicate material is particularly appealing, not only because of its green production process, but also because of its excellent performances and multiple functions of remediating the soil [8,9]. Primary studies proved that these excellent performances and functions were closely related to its physicochemical properties and mineral components [8,9]. Therefore, the study yields vital and valuable insights into comprehending the mineralogical properties of the K-feldspar and lime hydrothermal reaction and producing artificial silicate agrominerals from potassium-rich rocks.

Supplementary Materials

The following are available online at https://www.mdpi.com/2075-163X/9/1/46/s1, Element content and QPA; Nomenclature of grossular and hydrogarnet; Definition of the percentage of K-feldspar dissolution (D, %); Table S1: Overview of the hydrothermal reaction with reactant ratio (T = 190 °C, t = 13.6 h, and deionized water = 30 mL); Table S2: Quantitative phase analysis by the Rietveld method (%); Table S3: Element contents measured by ICP–OES and calculated from XRPD; Table S4: PDF data of hydrogarnet used in Figure 4a; Table S5: Estimated Si content, x, and Al/Si ratio of formed hydrogarnet from Equation (1) in this study; Table S6: EDS data of spherical and laminar particle in the sample L–6; Table S7: Percentage of K-feldspar dissolution and original data of Figure 9; Figure S1: Flow chart of mineral phases during the K-feldspar and lime hydrothermal reaction; Figure S2: XRPD of the residue of the filtrated solutions of the samples M–1 to M–9 dissolved in deionized water; Figure S3: A magnified view of XRPD pattern of M–1 to M–9 from 28.2° to 35°; Figure S4: A magnified view of XRPD pattern of L–1 to L–6 from 28.2° to 29.8°; Figure S5: Element contents of ICP–OES vs. XRPD: (a) the hydrothermal reaction with reaction temperature; (b) the hydrothermal reaction with reactant ratio.

Author Contributions

S.L. performed the experiments, analyzed the data and wrote the paper, C.H. and J.L. together presented the research plans and discussed the results.

Funding

This research project was supported by the Open Project Program of Key Laboratory of Mineral Resources, Institute of Geology and Geophysics, Chinese Academy of Sciences (No. KLMR2017-07), Projects in the National Science & Technology Pillar Program during the Eleventh Five-Year Plan Period (China, No. 2006BAD10B04), and the Knowledge Innovation Project of Chinese Academy of Sciences and Spark Program of China (No. 2007EA173003).

Acknowledgments

The authors were appreciated for the precious comments and suggestions of the editor and two reviewers.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Klein, C.; Philpotts, A.R. Chapter 7 Igneous rock-forming minerals. In Earth Materials: Introduction to Mineralogy and Petrology, 2nd ed.; Klein, C., Philpotts, A.R., Eds.; Cambridge University Press: New York, NY, USA, 2017; p. 161. [Google Scholar]
  2. Xu, Y.; Liang, X.; Xu, Y.; Qin, X.; Huang, Q.; Wang, L.; Sun, Y. Remediation of heavy metal-polluted agricultural soils using clay minerals: A review. Pedosphere 2017, 27, 193–204. [Google Scholar] [CrossRef]
  3. Guo, B.; Liu, B.; Yang, J.; Zhang, S. The mechanisms of heavy metal immobilization by cementitious material treatments and thermal treatments: A review. J. Environ. Manag. 2017, 193, 410–422. [Google Scholar] [CrossRef] [PubMed]
  4. Misaelides, P. Application of natural zeolites in environmental remediation: A short review. Microporous Mesoporous Mater. 2011, 144, 15–18. [Google Scholar] [CrossRef]
  5. Liu, J.M.; Liu, S.K.; Han, C.; Sheng, X.B.; Qi, X.; Zhang, Z.L. Mineral technology for soil remediation and improvement: A new applied research direction from mineralogy, petrology and geochemistry. Bull. Mineral. Petrol. Geochem. 2014, 33, 556–560. [Google Scholar]
  6. Han, C.; Liu, J.M. Method for Preparing Microporous Mineral Fertilizer from Silicates Rock Using Hydrothermal Chemical Reaction. Patent WO2009070953A1, 5 December 2007. [Google Scholar]
  7. Han, C. Method for Producing Micropore Silicon-Potassium-Calcium Mineral Fertilizer. Patent CN101054313B, 26 April 2007. [Google Scholar]
  8. Liu, S.K.; Qi, X.; Han, C.; Liu, J.M.; Sheng, X.B.; Li, H.; Luo, A.M.; Li, J.L. Novel nano-submicron mineral-based soil conditioner for sustainable agricultural development. J. Clean. Prod. 2017, 149, 896–903. [Google Scholar] [CrossRef]
  9. Liu, S.K.; Li, H.; Han, C.; Sheng, X.B.; Liu, J.M. Cd inhibition and pH improvement via a nano-submicron mineral-based soil conditioner. Environ. Sci. Pollut. Res. 2017, 24, 4942–4949. [Google Scholar] [CrossRef] [PubMed]
  10. Richardson, I.G. The calcium silicate hydrates. Cem. Concr. Res. 2008, 38, 137–158. [Google Scholar] [CrossRef]
  11. Komarneni, S.; Roy, D.M. Tobermorites: A new family of cation exchangers. Science 1983, 221, 647–648. [Google Scholar] [CrossRef] [PubMed]
  12. Zou, J.J.; Guo, C.B.; Zhou, X.Q.; Sun, Y.J.; Yang, Z. Sorption capacity and mechanism of Cr3+ on tobermorite derived from fly ash acid residue and carbide slag. Colloids Surf. A 2018, 538, 825–833. [Google Scholar] [CrossRef]
  13. Guo, X.L.; Shi, H.S. Microstructure and heavy metal adsorption mechanisms of hydrothermally synthesized Al-substituted tobermorite. Mater. Struct. 2017, 50, 10. [Google Scholar] [CrossRef]
  14. Yao, Z.D.; Tamura, C.; Matsuda, M.; Miyake, M. Resource recovery of waste incineration fly ash: Synthesis of tobermorite as ion exchanger. J. Mater. Res. 1999, 14, 4437–4442. [Google Scholar] [CrossRef]
  15. Rios, C.A.; Williams, C.D.; Fullen, M.A. Hydrothermal synthesis of hydrogarnet and tobermorite at 175 °C from kaolinite and metakaolinite in the CaO-Al2O3-SiO2-H2O system: A comparative study. Appl. Clay Sci. 2009, 43, 228–237. [Google Scholar] [CrossRef]
  16. Meller, N.; Kyritsis, K.; Hall, C. The mineralogy of the CaO-Al2O3-SiO2-H2O (CASH) hydroceramic system from 200 to 350 °C. Cem. Concr. Res. 2009, 39, 45–53. [Google Scholar] [CrossRef]
  17. Meller, N.; Hall, C.; Kyritsis, K.; Giriat, G. Synthesis of cement based CaO-Al2O3-SiO2-H2O (CASH) hydroceramics at 200 and 250 °C: Ex-situ and in-situ diffraction. Cem. Concr. Res. 2007, 37, 823–833. [Google Scholar] [CrossRef]
  18. Liu, S.K.; Han, C.; Liu, J.M.; Li, H. Research of extracting potassium, silica and aluminum from potassium feldspar by hydrothermal chemical reaction. Acta Mineral. Sin. 2009, 29, 320–326. [Google Scholar]
  19. Liu, S.K.; Han, C.; Liu, J.M.; Li, H. Hydrothermal decomposition of potassium feldspar under alkaline conditions. RSC Adv. 2015, 5, 93301–93309. [Google Scholar] [CrossRef]
  20. Ciceri, D.; de Oliveira, M.; Allanore, A. Potassium fertilizer via hydrothermal alteration of K-feldspar ore. Green Chem. 2017, 19, 5187–5202. [Google Scholar] [CrossRef]
  21. Skorina, T.; Allanore, A. Alkali Metal Ion Source with Moderate Rate of Ion Release and Methods of Forming. U.S. Patent US9340465B2, 6 May 2013. [Google Scholar]
  22. Liu, S.; Han, C.; Liu, J. Study of K-feldspar and lime hydrothermal reaction at 190 °c: Phase, kinetics and mechanism with reaction time. ChemistrySelect 2018, 3, 13010–13016. [Google Scholar] [CrossRef]
  23. Larson, A.C.; Von Dreele, R.B. General Structure Analysis System (GSAS); Los Alamos National Laboratory Report LAUR; Los Alamos National Laboratory: New Mexico, NM, USA, 2004; pp. 86–748. [Google Scholar]
  24. Toby, B.H. EXPGUI, a graphical user interface for GSAS. J. Appl. Crystallogr. 2001, 34, 210–213. [Google Scholar] [CrossRef]
  25. Rietveld, H.M. A profile refinement method for nuclear and magnetic structures. J. Appl. Crystallogr. 1969, 2, 65–71. [Google Scholar] [CrossRef] [Green Version]
  26. Reardon, E.J.; Fagan, R. The calcite/portlandite phase boundary: Enhanced calcite solubility at high pH. Appl. Geochem. 2000, 15, 327–335. [Google Scholar] [CrossRef]
  27. Pabst, A. Synthesis, properties, and structure of K2Ca(CO3)2, Bütschliite. Am. Mineral. 1974, 59, 353–358. [Google Scholar]
  28. Al-Wakeel, E.I.; El-Korashy, S.A. Reaction mechanism of the hydrothermally treated CaO-SiO2-Al2O3 and CaO-SiO2-Al2O3-CaSO4 systems. J. Mater. Sci. 1996, 31, 1909–1913. [Google Scholar] [CrossRef]
  29. Klimesch, D.S.; Ray, A. DTA-TG study of the CaO-SiO2-H2O and CaO-Al2O3-SiO2-H2O systems under hydrothermal conditions. J. Therm. Anal. Calorim. 1999, 56, 27–34. [Google Scholar] [CrossRef]
  30. Klimesch, D.S.; Ray, A. DTA-TGA evaluations of the CaO-Al2O3-SiO2-H2O system treated hydrothermally. Thermochim. Acta 1999, 334, 115–122. [Google Scholar] [CrossRef]
  31. Watanabe, O.; Kitamura, K.; Maenami, H.; Ishida, H. Hydrothermal treatment of a silica sand complex with lime. J. Am. Ceram. Soc. 2001, 84, 2318–2322. [Google Scholar] [CrossRef]
  32. Kyritsis, K.; Meller, N.; Hall, C. Chemistry and morphology of hydrogarnets formed in cement-based CASH hydroceramics cured at 200 to 350 °C. J. Am. Ceram. Soc. 2009, 92, 1105–1111. [Google Scholar] [CrossRef]
  33. Guo, X.L.; Meng, F.J.; Shi, H.S. Microstructure and characterization of hydrothermal synthesis of Al-substituted tobermorite. Constr. Build. Mater. 2017, 133, 253–260. [Google Scholar] [CrossRef]
  34. Organova, N.I.; Koporulina, E.V.; Ivanova, A.G.; Trubkini, N.V.; Zadov, A.E.; Khomyakov, A.P.; Marcille, I.M.; Chukanov, N.V.; Shmakov, A.N. Structure model of Al,K-substituted tobermorite and structural changes upon heating. Crystallogr. Rep. 2002, 47, 950–956. [Google Scholar] [CrossRef]
  35. Hu, X.L.; Yanagisawa, K.; Onda, A.; Kajiyoshi, K. Stability and phase relations of dicalcium silicate hydrates under hydrothermal conditions. J. Ceram. Soc. Jpn. 2006, 114, 174–179. [Google Scholar] [CrossRef]
  36. Pena, R.; Guerrero, A.; Goni, S. Hydrothermal treatment of bottom ash from the incineration of municipal solid waste: Retention of Cs(I), Cd(II), Pb(II) and Cr(III). J. Hazard. Mater. 2006, 129, 151–157. [Google Scholar] [CrossRef] [PubMed]
  37. Coleman, N.J. Interactions of Cd(II) with waste-derived 11 angstrom tobermorites. Sep. Purif. Technol. 2006, 48, 62–70. [Google Scholar] [CrossRef]
  38. Hinsinger, P. Potassium. In Encyclopedia of Soil Science; Lal, R., Ed.; Marcel Dekker Inc.: New York, NY, USA, 2002; pp. 1354–1358. [Google Scholar]
  39. Xu, R.K.; Zhao, A.Z.; Yuan, J.H.; Jiang, J. pH buffering capacity of acid soils from tropical and subtropical regions of China as influenced by incorporation of crop straw biochars. J. Soils Sediments 2012, 12, 494–502. [Google Scholar] [CrossRef]
  40. Weaver, A.R.; Kissel, D.E.; Chen, F.; West, L.T.; Adkins, W.; Rickman, D.; Luvall, J.C. Mapping soil pH buffering capacity of selected fields in the coastal plain. Soil Sci. Soc. Am. J. 2004, 68, 662–668. [Google Scholar] [CrossRef]
  41. Biagioni, C.; Merlino, S.; Bonaccorsi, E. The tobermorite supergroup: A new nomenclature. Mineral. Mag. 2015, 79, 485–495. [Google Scholar] [CrossRef]
  42. Wang, Z.H.; Ma, S.H.; Zheng, S.L.; Wang, X.H. Incorporation of Al and Na in Hydrothermally Synthesized Tobermorite. J. Am. Ceram. Soc. 2017, 100, 792–799. [Google Scholar] [CrossRef]
  43. Matsui, K.; Kikuma, J.; Tsunashima, M.; Ishikawa, T.; Matsuno, S.-Y.; Ogawa, A.; Sato, M. In situ time-resolved X-ray diffraction of tobermorite formation in autoclaved aerated concrete: Influence of silica source reactivity and Al addition. Cem. Concr. Res. 2011, 41, 510–519. [Google Scholar] [CrossRef]
  44. Maeda, H.; Abe, K.; Ishida, E.H. Hydrothermal synthesis of aluminum substituted tobermorite by using various crystal phases of alumina. J. Ceram. Soc. Jpn. 2011, 119, 375–377. [Google Scholar] [CrossRef] [Green Version]
  45. Grew, E.S.; Locock, A.J.; Mills, S.J.; Galuskina, I.O.; Galuskin, E.V.; Halenius, U. Nomenclature of the garnet supergroup. Am. Mineral. 2013, 98, 785–810. [Google Scholar] [CrossRef]
  46. Cohenaddad, C.; Ducros, P.; Bertaut, E.F. Etude de la substitution du groupement SiO4 par (OH)4 dans les composes Al2Ca3(OH)12 et Al2Ca3(SiO4)2,16(OH)3,36 de type grenat. Acta Crystallogr. 1967, 23, 220–230. [Google Scholar] [CrossRef]
  47. Oneill, B.; Bass, J.D.; Rossman, G.R. Elastic properties of hydrogrossular garnet and implications for water in the upper-mantle. J. Geophys. Res. Solid Earth 1993, 98, 20031–20037. [Google Scholar] [CrossRef]
  48. Okoronkwo, M.U.; Glasser, F.P. Compatibility of hydrogarnet, Ca3Al2(SiO4)(x)(OH)(4(3-x)), with sulfate and carbonate-bearing cement phases: 5–85 °C. Cem. Concr. Res. 2016, 83, 86–96. [Google Scholar] [CrossRef]
  49. Adhikari, P.; Dharmawardhana, C.C.; Ching, W.Y. Structure and properties of hydrogrossular mineral series. J. Am. Ceram. Soc. 2017, 100, 4317–4330. [Google Scholar] [CrossRef]
  50. Galvankova, L.; Masilko, J.; Solny, T.; Stepankova, E. Tobermorite synthesis under hydrothermal conditions. In Ecology and New Building Materials and Products 2016; Drdlova, M., Kubatova, D., Bohac, M., Eds.; Elsevier Science Bv: Amsterdam, The Netherlands, 2016; Volume 151, pp. 100–107. [Google Scholar]
  51. Maeda, H.; Kurosaki, Y.; Nakamura, T.; Nakayama, M.; Ishida, E.H.; Kasuga, T. Control of chemical composition of hydrogrossular prepared by hydrothermal reaction. Mater. Lett. 2014, 131, 132–134. [Google Scholar] [CrossRef]
  52. Grangeon, S.; Fernandez-Martinez, A.; Baronnet, A.; Marty, N.; Poulain, A.; Elkaim, E.; Roosz, C.; Gaboreau, S.; Henocq, P.; Claret, F. Quantitative X-ray pair distribution function analysis of nanocrystalline calcium silicate hydrates: A contribution to the understanding of cement chemistry. J. Appl. Crystallogr. 2017, 50, 14–21. [Google Scholar] [CrossRef] [PubMed]
  53. Hou, D.S.; Ma, H.Y.; Li, Z.J. Morphology of calcium silicate hydrate (C-S-H) gel: A molecular dynamic study. Adv. Cem. Res. 2015, 27, 135–146. [Google Scholar] [CrossRef]
  54. Grangeon, S.; Claret, F.; Lerouge, C.; Warmont, F.; Sato, T.; Anraku, S.; Numako, C.; Linard, Y.; Lanson, B. On the nature of structural disorder in calcium silicate hydrates with a calcium/silicon ratio similar to tobermorite. Cem. Concr. Res. 2013, 52, 31–37. [Google Scholar] [CrossRef]
  55. Houston, J.R.; Maxwell, R.S.; Carroll, S.A. Transformation of meta-stable calcium silicate hydrates to tobermorite: Reaction kinetics and molecular structure from XRD and NMR spectroscopy. Geochem. Trans. 2009, 10, 14. [Google Scholar] [CrossRef] [PubMed]
  56. Lothenbach, B.; Scrivener, K.; Hooton, R.D. Supplementary cementitious materials. Cem. Concr. Res. 2011, 41, 1244–1256. [Google Scholar] [CrossRef]
  57. Shaw, S.; Clark, S.M.; Henderson, C.M.B. Hydrothermal formation of the calcium silicate hydrates, tobermorite (Ca5Si6O16(OH)(2) · 4H(2)O) and xonotlite (Ca6Si6O17(OH)(2)): An in situ synchrotron study. Chem. Geol. 2000, 167, 129–140. [Google Scholar] [CrossRef]
  58. Mitsuda, T.; Sasaki, K.; Ishida, H. Phase evolution during autoclaving process of aerated concrete. J. Am. Ceram. Soc. 1992, 75, 1858–1863. [Google Scholar] [CrossRef]
  59. Zhang, P.; Ma, H.W. The synthesis of tobermorite from potassium feldspar powder: An experimental study. Acta Petrol. Et Mineral. 2005, 24, 333–338. [Google Scholar]
  60. Qiu, M.Y.; Ma, H.W.; Nie, Y.M.; Zhang, P.; Liu, H. Experimental study on synthesis of tobermorite by decomposing potassium feldspar. Geoscience 2005, 19, 348–354. [Google Scholar]
  61. Klimesch, D.S.; Ray, A. Effects of quartz particle size and kaolin on hydrogarnet formation during autoclaving. Cem. Concr. Res. 1998, 28, 1317–1323. [Google Scholar] [CrossRef]
  62. Klimesch, D.S.; Ray, A. Hydrogarnet formation during autoclaving at 180 °C in unstirred metakaolin-lime-quartz slurries. Cem. Concr. Res. 1998, 28, 1109–1117. [Google Scholar] [CrossRef]
  63. Klimesch, D.S.; Ray, A. Autoclaved cement-quartz pastes with metakaolin additions. Adv. Cem. Based Mater. 1998, 7, 109–118. [Google Scholar] [CrossRef]
  64. Liu, Y.; Xia, H.; Ma, H. Kinetics of hydrothermal decomposition of potassium feldspar with calcium hydroxide. Adv. Mater. Res. 2012, 549, 65–69. [Google Scholar] [CrossRef]
  65. Skorina, T.; Allanore, A. Aqueous alteration of potassium-bearing aluminosilicate minerals: From mechanism to processing. Green Chem. 2015, 17, 2123–2136. [Google Scholar] [CrossRef]
  66. Eckert, J.O.; HungHouston, C.C.; Gersten, B.L.; Lencka, M.M.; Riman, R.E. Kinetics and mechanisms of hydrothermal synthesis of barium titanate. J. Am. Ceram. Soc. 1996, 79, 2929–2939. [Google Scholar] [CrossRef]
  67. Berger, G.; Beaufort, D.; Lacharpagne, J.C. Experimental dissolution of sanidine under hydrothermal conditions: Mechanism and rate. Am. J. Sci. 2002, 302, 663–685. [Google Scholar] [CrossRef]
Minerals 09 00046 g001 550
Figure 1. Estimated volume percentages for the most common minerals in the earth’s crust. The data are from the reference [1], and are normalized to 100%.
Figure 1. Estimated volume percentages for the most common minerals in the earth’s crust. The data are from the reference [1], and are normalized to 100%.
Minerals 09 00046 g001
Minerals 09 00046 g002 550
Figure 2. Results of quantitative phase analysis by the Rietveld method: (a) with reaction temperature; (b) with Ca/Si molar ratio (see the detail of the reactant ratio in Table S1). Abbreviations: M—K-feldspar [KAlSi3O8]; S—Calcium hydroxide [slaked lime (portlandite), Ca(OH)2]; C—Calcite [CaCO3]; P—Potassium carbonate [K2CO3]; B—Bütschliite [K2CaCO3]; G—Grossular [Ca3Al2(SiO4)1.53(OH)5.88]; D—alpha-dicalcium silicate hydrate [α-C2SH, Ca2(SiO3OH)(OH)]; T—Tobermorite [Ca2.25(Si3O7.5(OH)1.5)(H2O)]; A—Amorphous phase.
Figure 2. Results of quantitative phase analysis by the Rietveld method: (a) with reaction temperature; (b) with Ca/Si molar ratio (see the detail of the reactant ratio in Table S1). Abbreviations: M—K-feldspar [KAlSi3O8]; S—Calcium hydroxide [slaked lime (portlandite), Ca(OH)2]; C—Calcite [CaCO3]; P—Potassium carbonate [K2CO3]; B—Bütschliite [K2CaCO3]; G—Grossular [Ca3Al2(SiO4)1.53(OH)5.88]; D—alpha-dicalcium silicate hydrate [α-C2SH, Ca2(SiO3OH)(OH)]; T—Tobermorite [Ca2.25(Si3O7.5(OH)1.5)(H2O)]; A—Amorphous phase.
Minerals 09 00046 g002
Minerals 09 00046 g003 550
Figure 3. Enlargement of the diffraction peak of tobermorite (002). The sample (Tob) without Al was synthesized with a 0.83 Ca/Si molar ratio under the same temperature, time and water/solid ratio to those of M–1 to M–9, and Ca and Si sources were from lime and fumed silica powder, respectively. Data of Tm–6 to Tm–10 were from the previous publication [22].
Figure 3. Enlargement of the diffraction peak of tobermorite (002). The sample (Tob) without Al was synthesized with a 0.83 Ca/Si molar ratio under the same temperature, time and water/solid ratio to those of M–1 to M–9, and Ca and Si sources were from lime and fumed silica powder, respectively. Data of Tm–6 to Tm–10 were from the previous publication [22].
Minerals 09 00046 g003
Minerals 09 00046 g004 550
Figure 4. (a) Plot of Si content against lattice parameter a of hydrogarnet from the powder diffraction file (PDF) data (see Table S4); (b) plot of Si content of hydrogarnet calculated from Equation (1) against nominal Ca/Si molar ratio in the starting material (see Table S5).
Figure 4. (a) Plot of Si content against lattice parameter a of hydrogarnet from the powder diffraction file (PDF) data (see Table S4); (b) plot of Si content of hydrogarnet calculated from Equation (1) against nominal Ca/Si molar ratio in the starting material (see Table S5).
Minerals 09 00046 g004
Minerals 09 00046 g005 550
Figure 5. Diffraction peak from hydrogarnet (420) with various hydrothermal conditions: (a) reaction temperature; (b) Ca/Si molar ratio (NCa/Si); (c) reaction time (data of Tm–3 to Tm–10 were from the previous publication [22]).
Figure 5. Diffraction peak from hydrogarnet (420) with various hydrothermal conditions: (a) reaction temperature; (b) Ca/Si molar ratio (NCa/Si); (c) reaction time (data of Tm–3 to Tm–10 were from the previous publication [22]).
Minerals 09 00046 g005
Minerals 09 00046 g006 550
Figure 6. SEM images: (a) K-feldspar and (b) lime.
Figure 6. SEM images: (a) K-feldspar and (b) lime.
Minerals 09 00046 g006
Minerals 09 00046 g007 550
Figure 7. SEM images: (a) L–1; (b) L–2; (c) L–3; (d) L–4; (e) L–5 and (f) L–6.
Figure 7. SEM images: (a) L–1; (b) L–2; (c) L–3; (d) L–4; (e) L–5 and (f) L–6.
Minerals 09 00046 g007
Minerals 09 00046 g008 550
Figure 8. SEM magnified image of L–6: (a) spots of energy dispersive X-ray spectroscopy (EDS) for spherical particle; (b) spots of EDS for laminar particle. EDS were determined for the spots in the black circles.
Figure 8. SEM magnified image of L–6: (a) spots of energy dispersive X-ray spectroscopy (EDS) for spherical particle; (b) spots of EDS for laminar particle. EDS were determined for the spots in the black circles.
Minerals 09 00046 g008
Minerals 09 00046 g009 550
Figure 9. Natural logarithm of the percentage of dissolution (lnD) versus the reciprocal temperature (1/T, K−1). ● lnD; --- linear fit.
Figure 9. Natural logarithm of the percentage of dissolution (lnD) versus the reciprocal temperature (1/T, K−1). ● lnD; --- linear fit.
Minerals 09 00046 g009
Minerals 09 00046 g010 550
Figure 10. Hydrothermal dissolution mechanism of K-feldspar from 130 °C to 250 °C.
Figure 10. Hydrothermal dissolution mechanism of K-feldspar from 130 °C to 250 °C.
Minerals 09 00046 g010
Table
Table 1. An overview of mineral phases with various reaction conditions.
Table 1. An overview of mineral phases with various reaction conditions.
Single FactorNCa/SiTemperatureTime (b)
Experimental conditionTemp = 190 °C130 °C ≤ Temp ≤ 250 °CTemp = 190 °C
Time = 13.6 hTime = 20 h0 h ≤ Time ≤ 36 h
0.72 ≤ NCa/Si ≤ 3.91NCa/Si = 1.37NCa/Si = 1.37
M (a)allallall
SNCa/Si ˃ 1.37130 °C ≤ Temp < 190 °CTime < 16 h
Callallall
P/130 °C ≤ Temp < 190 °C4 h < Time < 16 h
BallTemp ˃ 160 °CTime ˃ 8 h
GallallTime ˃ 4 h
DNCa/Si ˃ 1.1216 °C < Temp < 220 °C8 h < Time < 32 h
TNCa/Si < 1.68Temp ˃ 160 °CTime ˃ 16 h
Aallallall
Note: (a) Abbreviations: M—K-feldspar [KAlSi3O8]; S—Calcium hydroxide [slaked lime (portlandite), Ca(OH)2]; C—Calcite [CaCO3]; P—Potassium carbonate [K2CO3]; B—Bütschliite [K2CaCO3]; G—Grossular [Ca3Al2(SiO4)1.53(OH)5.88]; D—alpha-dicalcium silicate hydrate [α-C2SH, Ca2(SiO3OH)(OH)]; T—Tobermorite [Ca2.25(Si3O7.5(OH)1.5)(H2O)]; A—Amorphous phase; (b) the data of phase with reaction time are cited from the previous work [22].

Share and Cite

MDPI and ACS Style

Liu, S.; Han, C.; Liu, J. Study of K-Feldspar and Lime Hydrothermal Reaction: Phase and Mechanism with Reaction Temperature and Increasing Ca/Si Ratio. Minerals 2019, 9, 46. https://doi.org/10.3390/min9010046

AMA Style

Liu S, Han C, Liu J. Study of K-Feldspar and Lime Hydrothermal Reaction: Phase and Mechanism with Reaction Temperature and Increasing Ca/Si Ratio. Minerals. 2019; 9(1):46. https://doi.org/10.3390/min9010046

Chicago/Turabian Style

Liu, Shanke, Cheng Han, and Jianming Liu. 2019. "Study of K-Feldspar and Lime Hydrothermal Reaction: Phase and Mechanism with Reaction Temperature and Increasing Ca/Si Ratio" Minerals 9, no. 1: 46. https://doi.org/10.3390/min9010046

APA Style

Liu, S., Han, C., & Liu, J. (2019). Study of K-Feldspar and Lime Hydrothermal Reaction: Phase and Mechanism with Reaction Temperature and Increasing Ca/Si Ratio. Minerals, 9(1), 46. https://doi.org/10.3390/min9010046

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop