Representativity of 2D Shape Parameters for Mineral Particles in Quantitative Petrography
Abstract
:1. Introduction
1.1. Overview
1.2. Shape Parameter Quantification
1.3. Objectives
2. Materials and Methods
2.1. Design and Development of Type Particles
2.2. Parameters and Measurement Techniques
2.3. Determination of Analysis Conditions
2.4. Data Acquisition and Evaluation
2.5. Estimation of a Regularity Indicator (RBC)
2.6. Application to A Case Study and Validation
3. Results
3.1. Description of Type Particles
3.2. Optimal Analysis Conditions of Shape Parameters
3.3. Shape Parameter Evaluation and A New Regularity Indicator (RBC)
3.3.1. Shape Parameter Evaluation
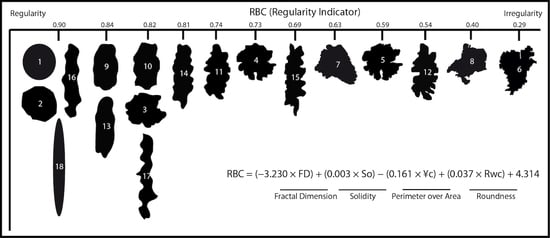
3.3.2. New Regularity Indicator (RBC)
3.4. Application and Validation of Shape Parameters
4. Discussion
4.1. Representativity of the Shape Parameters Studied
4.2. Minimum Particle Size for Shape Analysis
4.3. Application of the Proposed Indicator of Regularity
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Barrett, P.J. The shape of rock particles, a critical review. Sedimentology 1980, 27, 291–303. [Google Scholar] [CrossRef]
- Cho, G.C.; Dods, J.; Santamarina, J.C. Particle shape efects o packing density, stiffness and strength: Natural and crushed sands. J. Geotech. Geoenviron. Eng. 2006, 132, 591–602. [Google Scholar] [CrossRef] [Green Version]
- Tucker, M.E. Sedimentary Petrology: An Introduction to the Origin of Sedimentary Rocks, 3rd ed.; Blackwell Publishing Limited: Oxford, UK, 2001; 272p. [Google Scholar]
- Mitchell, J.K.; Soga, K. Soil composition and engineering properties. In Fundamentals of Soil Behavior, 3rd ed.; John Wiley & Sons: Hoboken, NY, USA, 2005; pp. 83–106. [Google Scholar]
- Blott, S.J.; Pye, K. Particle shape: A review and new methods of characterization and classification. Sedimentology 2008, 55, 31–63. [Google Scholar] [CrossRef]
- Krumbein, W.C.; Sloss, L.L. Stratigraphy and Sedimentation; W.H. Freeman and Company: San Francisco, CA, USA, 1951; 497p. [Google Scholar]
- Powers, M.C. A new roundness scale for Sedimentology particles. J. Sediment. Petrol. 1953, 23, 117–119. [Google Scholar] [CrossRef]
- Pettijohn, F.J.; Potter, P.E.; Siever, R. Sand and Sandstone; Springer: New York, NY, USA; Berlin/Heidelberg, Germany, 1973; 618p. [Google Scholar]
- Nichols, G. Sedimentology and Stratigraphy; Wiley-Blackwell: Oxford, UK, 2009; 419p. [Google Scholar]
- Wentworth, C.K. The Shapes of Beach Pebbles; US Government Printing Office: Washington, DC, USA, 1919; Volume 131, pp. 75–83. [Google Scholar]
- Wadell, H.A. Sphericity and roundness of rock particles. J. Geol. 1933, 41, 310–331. [Google Scholar] [CrossRef]
- Lees, G. A new method for determining the angularity of particles. Sedimentology 1964, 3, 2–21. [Google Scholar] [CrossRef]
- Sukumaran, B.; Ashmawy, A.K. Quantitative characterisation of the geometry of discrete particles. Geotechnique 2001, 51, 619–627. [Google Scholar] [CrossRef]
- Cox, E.P. A method of assigning numerical and percentage values to the degree of roundness of sand grains. J. Paleontol. 1927, 1, 179–183. [Google Scholar]
- Janoo, V. Quantification of Shape, Angularity, and Surface Texture of Base Course Materials (No. CRREL-SR-98-1); US Army Corps of Engineers: Washington, DC, USA, 1998; 28p. [Google Scholar]
- Fernández, F.J.; Menéndez-Duarte, R.; Aller, J.; Bastida, F. Application of geographical information systems to shape-fabric analysis. Geol. Soc. Lon. Spec. Pub. 2005, 245, 409–420. [Google Scholar] [CrossRef]
- Anselmetti, F.S.; Luthi, S.; Eberli, G.P. Quantitative characterization of carbonate pore systems by digital image analysis. AAPG Bull. 1998, 82, 1815–1836. [Google Scholar]
- Berrezueta, E.; Kovacs, T. Application of optical image analysis to the assessment of pore space evolution after CO2 injection in sandstones. A case study. J. Pet. Sci. Eng. 2017, 159, 679–690. [Google Scholar] [CrossRef]
- Preparata, F.P.; Shamos, M.I. Computational Geometry; Springer: New York, NY, USA, 1985; 390p. [Google Scholar]
- Melkman, A.A. On-line construction of the convex hull of simple polygon. Inf. Process. Lett. 1987, 25, 11–12. [Google Scholar] [CrossRef]
- Liu, E.J.; Cashman, K.V.; Rust, A.C. Optimizing shape analysis to quantify volcanic ash morphology. GeoResJ. 2015, 8, 14–30. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Ma, G.; Wang, H.; He, P.; Liu, M.; Wang, H.; Xu, B. Comparison of solidity and fractal dimension of plasma sprayed splat with different spreading morphologies. Appl. Surf. Sci. 2017, 409, 277–284. [Google Scholar] [CrossRef]
- Wadell, H.A. Volume, shape and roundness of rock particles. J. Geol. 1932, 40, 443–451. [Google Scholar] [CrossRef]
- Roussillon, T.; Piégay, H.; Sivignon, I.; Tougne, L.; Lavigne, F. Automatic computation of pebble roundness using digital imagery and discrete geometry. Comput. Geosci. 2009, 35, 1992–2000. [Google Scholar] [CrossRef]
- Rittenhouse, G. A visual method of estimating two-dimensional sphericity. J. Sediment. Petrol. 1943, 13, 79–81. [Google Scholar]
- Mandelbrot, B.B. Fractals: Form, Chance and Dimension; W.H. Freeman & Company: San Francisco, CA, USA, 1977; 365p. [Google Scholar]
- Vallejo, L.E. Fractal analysis of granular materials. Geotechnique 1995, 45, 159–163. [Google Scholar] [CrossRef]
- Vallejo, L.E. Fractals in engineering geology preface. Eng. Geol. 1997, 48, 159–160. [Google Scholar] [CrossRef]
- Hyslip, J.P.; Vallejo, L.E. Fractal analysis of the roughness and size distribution of granular materials. Eng. Geol. 1997, 48, 231–244. [Google Scholar] [CrossRef]
- Araujo, G.S.; Bicalho, K.V.; Tristao, F.A. Use of digital image analysis combined with fractal theory to determine particle morphology and surface texture of quartz sands. J. Rock Mech. Geotech. Eng. 2017, 9, 1131–1139. [Google Scholar] [CrossRef]
- Richardson, L. The problem of contiguity: An appendix to statistics of deadly quarrels. Gen. Syst. Yearb. 1961, 6, 139–187. [Google Scholar]
- Santamarina, J.C.; Cho, G.C. Soil Behavior: The Role of Particle Shape. In Proceedings of the Advances in Geotechnical Engineering: The Skempton Conference, London, UK, 29–31 March 2004. [Google Scholar]
- Rodríguez, J.; Edeskär, T.; Knutsson, S. Particle shape quantities and measurement techniques: A review. Electron. J. Geotechnique Eng. 2013, 18, 169–198. [Google Scholar]
- He, H.; Courard, L.; Pirard, E.; Michel, F. Shape analysis of fine aggregates used for concrete. Image Anal. Stereol. 2016, 35, 159–166. [Google Scholar] [CrossRef] [Green Version]
- Igathinathane, C.; Pordesimo, L.O.; Columbus, E.P.; Batchelor, W.D.; Methuku, S.R. Shape identification and particles size distribution from basic shape parameters using ImageJ. Comput. Electron. Agric. 2008, 63, 168–182. [Google Scholar] [CrossRef]
- Zheng, J.; Hryciw, R.D. Traditional soil particle sphericity, roundness and surface roughness by computational geometry. Geotechnique 2015, 65, 494–506. [Google Scholar] [CrossRef]
- Zheng, J.; Hryciw, R.D. Roundness and sphericity of soil particles in assemblies by computational geometry. J. Comput. Civ. Eng. 2016, 30, 04016021. [Google Scholar] [CrossRef]
- Zang, Z.X.; Yan, C.G.; Dong, Z.Y.; Huang, J.; Zang, Y.F. Granger causality analysis implementation on MATLAB: A graphic user interface toolkit for fMRI data processing. J. Neurosci. Methods 2012, 203, 418–426. [Google Scholar] [CrossRef]
- Liu, K.; Ostadhassan, M. Multi-scale fractal analysis of pores in shale rocks. J. Appl. Geophys. 2017, 140, 1–10. [Google Scholar] [CrossRef]
- Berrezueta, E.; González-Menéndez, L.; Ordóñez-Casado, B.; Olaya, P. Pore network quantification of sandstones under experimental CO2 injection using image analysis. Comput. Geosci. 2015, 77, 97–110. [Google Scholar] [CrossRef]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef] [PubMed]
- Vallejo, L.E.; Zhou, Y. The relationship between the fractal dimension and Krumbein‘s roundness number. Soils Found. 1995, 35, 163–167. [Google Scholar] [CrossRef] [Green Version]
- Krumbein, W.C. Measurement and geological significance of shape and roundness of sedimentary particles. J. Sedimentol. Res. 1941, 11, 64–72. [Google Scholar] [CrossRef]
- Takashimizu, Y.; Iiyoshi, M. New parameter of roundness R: Circularity corrected by aspect ratio. Prog. Earth Planet. Sci. 2016, 3, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Berrezueta, E.; Domínguez-Cuesta, M.J.; Ordóñez-Casado, B.; Medina, C.; Molinero, R. Pore space quantification of sedimentary rocks before-after Supercritical CO2 Interaction by Optical Image Analysis. Energy Procedia 2017, 114, 4382–4393. [Google Scholar] [CrossRef]
- Altuhafi, F.; O’Sullivan, C.; Cavarretta, I. Analysis of an image-based method to quantify the size and shape of sand particles. J. Geotech. Geoenviron. Eng. 2013, 139, 1290–1307. [Google Scholar] [CrossRef]
- Vangla, P.; Roy, N.; Gali, M.L. Image based shape characterization of granular materials and its effect on kinematics of particle motion. Granul. Mater. 2018, 20, 6. [Google Scholar] [CrossRef]
- Krumbein, W.C. The effects of abrasion on the size, shape and roundness of rock fragments. J. Geol. 1941, 49, 482–520. [Google Scholar] [CrossRef]
- Cuervas-Mons, J. Estudio de Partículas Minerales Mediante Procesamiento de Imágenes Digitales: Análisis Cualitativo—Cuantitativo de Parámetros de Forma; Trabajo Fin de Máster; Universidad de Oviedo: Oviedo, Spain, 2019; 62p. [Google Scholar]
- Russel, R.D.; Taylor, R.E. Roundness and shape of Mississippi river sands. J. Geol. 1937, 45, 225–267. [Google Scholar] [CrossRef]
- Pettijohn, F.J. Sedimentary Rocks, 2nd ed.; Harper and Brothers: New York, NY, USA, 1957; 718p. [Google Scholar]
- Hawkins, A.E. The Shape of Powder-Particle Outlines; Research Studies Press: Taunton, UK; J. Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Berrezueta, E.; González-Menéndez, L.; Breitner, D.; Luquot, L. Pore system changes during experimental CO2 injection into detritic rocks: Studies of potential storage rocks from some sedimentary basins of Spain. Int. J. Greenh. Gas Control 2013, 17, 411–422. [Google Scholar] [CrossRef]
- Olaya, P. Caracterización Petrográfica Mineralógica Automatizada de Rocas Con Potencial Para Almacenar CO2. Bachelor’s Thesis, Facultad de Ingeniería en Ciencias de la Tierra (FICT), Escuela Superior Politécnica del Litoral (Espol), Guayaquil, Ecuador, 2011; 110p. [Google Scholar]
- Hryciw, R.D.; Zheng, J.; Shetler, K. Particle roundness and sphericity from images of assemblies by chart estimates and computer methods. J. Geotech. Geoenviron. Eng. 2016, 142, 04016038. [Google Scholar] [CrossRef]
- Cassel, M.; Piégay, H.; Lavé, J.; Vaudor, L.; Sri, D.H.; Budi, S.W.; Lavigne, F. Evaluating a 2D image-based computerized approach for measuring pebble roundness. Geomorphology 2018, 311, 143–157. [Google Scholar] [CrossRef]
- Saint-Cyr, B.; Delenne, J.Y.; Radjai, F.; Sornay, P. Rheology of granular materials composed of nonconvex particles. Phys. Rev. E 2011, 84, 041302. [Google Scholar] [CrossRef] [PubMed]












| Properties | Shape Parameters | References |
|---|---|---|
| Sphericity (form) | Wadell’s circularity | [11,23] |
| Sphericity | [6] | |
| Ellipticity-aspect ratio-elongation | [16,24] | |
| Rittenhouse’s sphericity | [25] | |
| Roundness | Wentworth’s roundness | [10] |
| Wadell’s roundness | [11] | |
| Angularity | [12] | |
| Shape Factor | [13] | |
| Angularity Factor | ||
| Circularity of Cox/ Shape factor | [14,15,16] | |
| Perimeter over area normalized ratio | [17] | |
| Solidity-convexity | [19,20] | |
| Krumbein’s roundness number | [43] | |
| Roundness | [44] | |
| Roughness (surface texture) | Fractal Dimension | [26,27,28,29,30] |
| Morphological Parameter | Mathematical Expression | Software |
|---|---|---|
| Roundness (Rw) [11]. where ri is the radius of curvature of each corner, N is the number of corners, and rins is the radius of the maximum circle inscribed in the particle. | Custom application in DOS OS Roussillon Toolbox [24] | |
| Sphericity (S) [6]. where d1 is the length of the particle and d2 is the width. | ImageJ (v. 1.52) | |
| Solidity-convexity (So) [19,20]. where AT is the area of the particle, and Aconvex is the area defined by the convexity produced by the irregularity of the edge of the particle. | ImageJ (v. 1.52) | |
| Fractal Dimension (FD) [26]. | Richardson Method [31] | Image-Pro Plus® (v.7) |
| ¥ (normalized PoA) [17]. where Pi and Ai are, respectively, the perimeter and the area measured for a particle. | ImageJ (v. 1.52) | |
| Sf (Shape factor) [14]. where Pi and Ai are, respectively, the perimeter and the area measured for a particle. | ImageJ (v. 1.52) |
| Objective | Camera Lenses | Total | Geometric Calibration µm/pixel | Minimum Ø (µm) Case a | Minimum Ø (µm) Case b |
|---|---|---|---|---|---|
| 40 | 0.63 | 25.32 | 0.156 | 23.4 | 7.80 |
| 20 | 0.63 | 12.66 | 0.312 | 46.8 | 15.60 |
| 10 | 0.63 | 6.33 | 0.624 | 93.6 | 31.20 |
| 5 | 0.63 | 3.17 | 1.248 | 187.2 | 62.40 |
| 4 | 0.63 | 2.52 | 1.564 | 234.6 | 78.20 |
| 2 | 0.63 | 1.26 | 3.120 | 468 | 156.00 |
| Particle | Shape Parameters | Linear Multiple Regression | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| FD | So | ¥c | Rwc | RBC1 | a, a2, σa | b, b2, σb | c, c2, σc | d, d2, σd | e, σe | RBC | |
| 1 | 1.0180 | 1.00 | 1.06 | 0.94 | 1.00 | −3.230 −0.692 0.787 | 0.003 0.001 0.339 | −0.161 −0.252 0.15 | 0.037 0.043 0.129 | 4.314 0.82 | 0.90 |
| 2 | 1.0137 | 0.99 | 1.08 | 0.67 | 0.95 | 0.90 | |||||
| 3 | 1.0209 | 0.88 | 1.31 | 0.42 | 0.90 | 0.82 | |||||
| 4 | 1.0358 | 0.86 | 1.57 | 0.38 | 0.70 | 0.73 | |||||
| 5 | 1.0657 | 0.83 | 1.83 | 0.26 | 0.55 | 0.59 | |||||
| 6 | 1.1608 | 0.80 | 1.85 | 0.62 | 0.40 | 0.29 | |||||
| 7 | 1.0801 | 0.90 | 1.32 | 0.55 | 0.50 | 0.63 | |||||
| 8 | 1.1339 | 0.78 | 1.63 | 0.49 | 0.45 | 0.41 | |||||
| 9 | 1.0317 | 0.97 | 1.10 | 0.91 | 0.85 | 0.84 | |||||
| 10 | 1.0335 | 0.92 | 1.19 | 0.90 | 0.80 | 0.82 | |||||
| 11 | 1.0459 | 0.85 | 1.41 | 0.82 | 0.65 | 0.74 | |||||
| 12 | 1.0812 | 0.81 | 1.97 | 0.78 | 0.55 | 0.54 | |||||
| 13 | 1.0333 | 0.96 | 1.06 | 0.94 | 0.80 | 0.84 | |||||
| 14 | 1.0389 | 0.88 | 1.15 | 0.91 | 0.65 | 0.81 | |||||
| 15 | 1.0544 | 0.78 | 1.55 | 0.82 | 0.60 | 0.69 | |||||
| 16 | 1.0174 | 0.81 | 1.09 | 0.94 | 0.95 | 0.90 | |||||
| 17 | 1.0208 | 0.66 | 1.43 | 0.91 | 0.90 | 0.82 | |||||
| 18 | 1.0130 | 1.00 | 1.12 | 0.73 | 0.95 | 0.90 | |||||
| Samples | Statistics | FD | So | Sf | ¥c | Rwc | S | RBC |
|---|---|---|---|---|---|---|---|---|
| SI sample 105 particles > 50 pixels | Average | 1.1353 | 0.82 | 0.40 | 1.65 | 0.57 | 0.61 | 0.40 |
| Standard deviation | 0.0557 | 0.09 | 0.16 | 0.36 | 0.14 | 0.16 | 0.23 | |
| SB sample 99 particles | Average | 1.1213 | 0.83 | 0.37 | 1.50 | 0.77 | 0.61 | 0.48 |
| Standard deviation | 0.0465 | 0.06 | 0.13 | 0.24 | 0.14 | 0.17 | 0.18 | |
| SB sample 68 particles > 50 pixels | Average | 1.1124 | 0.85 | 0.43 | 1.53 | 0.70 | 0.62 | 0.50 |
| Standard deviation | 0.0045 | 0.05 | 0.12 | 0.26 | 0.18 | 0.16 | 0.18 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berrezueta, E.; Cuervas-Mons, J.; Rodríguez-Rey, Á.; Ordóñez-Casado, B. Representativity of 2D Shape Parameters for Mineral Particles in Quantitative Petrography. Minerals 2019, 9, 768. https://doi.org/10.3390/min9120768
Berrezueta E, Cuervas-Mons J, Rodríguez-Rey Á, Ordóñez-Casado B. Representativity of 2D Shape Parameters for Mineral Particles in Quantitative Petrography. Minerals. 2019; 9(12):768. https://doi.org/10.3390/min9120768
Chicago/Turabian StyleBerrezueta, Edgar, José Cuervas-Mons, Ángel Rodríguez-Rey, and Berta Ordóñez-Casado. 2019. "Representativity of 2D Shape Parameters for Mineral Particles in Quantitative Petrography" Minerals 9, no. 12: 768. https://doi.org/10.3390/min9120768
APA StyleBerrezueta, E., Cuervas-Mons, J., Rodríguez-Rey, Á., & Ordóñez-Casado, B. (2019). Representativity of 2D Shape Parameters for Mineral Particles in Quantitative Petrography. Minerals, 9(12), 768. https://doi.org/10.3390/min9120768