Low Temperature Synthesis of Aegirine NaFeSi2O6: Spectroscopy (57Fe Mössbauer, Raman) and Size/Strain Analysis from X-ray Powder Diffraction
Abstract
:1. Introduction
2. Materials and Methods
2.1. Synthesis
2.2. High-Resolution Transmission Electron Microscopy (HRTEM)
2.3. X-ray Diffraction
2.4. Mössbauer Spectroscopy
2.5. Raman Spectroscopy
3. Results
3.1. Synthesis and Sample Morphology
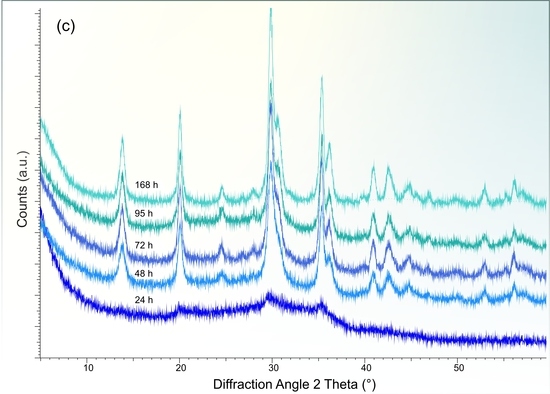
3.2. X-ray Diffraction Analysis
3.3. 57Fe Mössbauer Spectroscopy
3.4. Raman Spectroscopy
4. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Temperature (°C) | Duration (h) | Color | Phase Content |
|---|---|---|---|
| 130 | 24 | dark reddish brown | am (100) |
| 130 | 92 | dark reddish brown | am (100) |
| 130 | 142 | reddish brown | am (100) |
| 130 | 192 | Grey yellow | ae (80), am (20) |
| 130 | 310 | yellow | ae |
| 150 | 24 | Light yellow brown | am (90), ae (10) |
| 150 | 48 | yellow-green | ae |
| 150 | 72 | yellow-green | ae |
| 150 | 96 | yellow-green | ae |
| 150 | 120 | yellow-green | ae |
| 150 | 168 | yellow-green | ae |
| 155 | 24 | yellow | ae |
| 160 | 24 | yellow | ae |
| 170 | 24 | yellow | ae |
| 180 | 24 | yellow | ae |
| 190 | 24 | yellow | ae |
| 200 | 24 | yellow | ae |
| 210 | 24 | yellow | ae |
| 220 | 24 | pale yellow | ae |
| 225 | 24 | pale yellow | ae |
| 230 | 24 | pale yellow | ae |
| Annealing Experiment | |||
| 130, 500 | 24, 24 | intense red-brown | am |
| 130, 700 | 24, 24 | red-brown | ae (85), he (15) |
| 130, 900 | 24, 24 | red- brown | ae (87), he (13) |
| 200, 300 | 24, 24 | yellow | ae |
| 200, 400 | 24, 24 | yellow | ae |
| 200, 500 | 24, 24 | yellow | ae |
| 200, 550 | 24, 24 | yellow | ae |
| 200, 600 | 24, 24 | yellow | ae |
| 200, 650 | 24, 24 | yellow | ae |
| 200, 700 | 24, 24 | yellow | ae |
| 200, 750 | 24, 24 | yellow | ae |
| 200, 800 | 24, 24 | pale yellow | ae |
| 200, 850 | 24, 24 | pale yellow | ae |
| 200, 900 | 24, 24 | pale yellow | ae |
| Site | occ | x | y | z | Biso |
|---|---|---|---|---|---|
| Na | 0.5 | 0 | 0.3010 (7) | 0.25 | 2.4 (4) |
| Fe | 0.5 | 0 | 0.8984 (3) | 0.25 | 2.0 (4) |
| Si | 1.0 | 0.2899 (3) | 0.0898 (4) | 0.2334 (7) | 2.0 (3) |
| O1 | 1.0 | 0.1140 (5) | 0.0830 (8) | 0.1386 (9) | 2.1 (4) |
| O2 | 1.0 | 0.3584 (5) | 0.2564 (7) | 0.3025 (9) | 1.4 (4) |
| O3 | 1.0 | 0.3523 (6) | 0.0068 (5) | 0.0127 (2) | 2.5 (4) |







References
- Deer, W.A.; Howie, R.A.; Zussman, J. Single-Chain Silicates, 2nd ed.; Geological Soc.: London, UK, 2001; Volume 2A, p. VIII, 668 S. [Google Scholar]
- Decarreau, A.; Petit, S.; Vieillard, P.; Dabert, N. Hydrothermal synthesis of aegirine at 200 °C. Eur. J. Mineral. 2004, 16, 85–90. [Google Scholar] [CrossRef]
- Milton, C.; Eugster, H.P. Mineral assemblages of Green River formation. In Researches in Geochemistry; Abelson, H.P., Ed.; John Wiley & Sons: New York, NY, USA, 1959; pp. 118–150. [Google Scholar]
- Redhammer, G.J.; Amthauer, G.; Lottermoser, W.; Treutmann, W. Synthesis and structural properties of clinopyroxenes of the hedenbergite CaFe2+Si2O6-aegirine NaFe3+Si2O6 solid-solution series. Eur. J. Mineral. 2000, 12, 105–120. [Google Scholar] [CrossRef]
- Redhammer, G.J.; Amthauer, G.; Roth, G.; Tippelt, G.; Lottermoser, W. Single-crystal X-ray diffraction and temperature dependent 57Fe Mossbauer spectroscopy on the hedenbergite-aegirine (Ca,Na)(Fe2+,Fe3+)Si2O6 solid solution. Am. Mineral. 2006, 91, 1271–1292. [Google Scholar] [CrossRef]
- Dollase, W.A.; Gustafson, W.I. 57Fe Mossbauer spectral-analysis of the sodic clinopyroxenes. Am. Mineral. 1982, 67, 311–327. [Google Scholar]
- Redhammer, G.J.; Tippelt, G.; Amthauer, G.; Roth, G. Structural and 57Fe Mossbauer spectroscopic characterization of the synthetic NaFeSi2O6 (aegirine)-CaMgSi2O6 (diopside) solid solution series. Z. Fur Krist. 2012, 227, 396–410. [Google Scholar] [CrossRef]
- Nolan, J. Physical properties of synthetic and natural pyroxenes in the system diopside-hedenbergite-acmite. Mineral. Mag. 1969, 37, 216–229. [Google Scholar] [CrossRef]
- Yagi, K. System acmite-diopside and its bearing on stability relations of natural pyroxenes of acmite-hedenbergite-diopside series. Am. Mineral. 1966, 51, 976–1000. [Google Scholar]
- Redhammer, G.J.; Camara, F.; Alvaro, M.; Nestola, F.; Tippelt, G.; Prinz, S.; Simons, J.; Roth, G.; Amthauer, G. Thermal expansion and high-temperature P21/c-C2/c phase transition in clinopyroxene-type LiFeGe2O6 and comparison to NaFe(Si,Ge)2O6. Phys. Chem. Miner. 2010, 37, 685–704. [Google Scholar] [CrossRef]
- Secco, L.; Guastoni, A.; Nestola, F.; Redhammer, G.J.; Dal Negro, A. Crystal chemistry of aegirine as an indicator of P-T conditions. Mineral. Mag. 2007, 71, 321–326. [Google Scholar] [CrossRef]
- Jodlauk, S.; Becker, P.; Mydosh, J.A.; Khomskii, D.I.; Lorenz, T.; Streltsov, S.V.; Hezel, D.C.; Bohaty, L. Pyroxenes: A new class of multiferroics. J. Phys. Condens. Matter 2007, 19, 432201. [Google Scholar] [CrossRef]
- Redhammer, G.J.; Roth, G.; Paulus, W.; Andre, G.; Lottermoser, W.; Amthauer, G.; Treutmann, W.; Koppelhuber-Bitschnau, B. The crystal and magnetic structure of Li-aegirine LiFe3+Si2O6: a temperature-dependent study. Phys. Chem. Miner. 2001, 28, 337–346. [Google Scholar] [CrossRef]
- Redhammer, G.J.; Roth, G.; Treutmann, W.; Hoelzel, M.; Paulus, W.; Andre, G.; Pietzonka, C.; Amthauer, G. The magnetic structure of clinopyroxene-type LiFeGe2O6 and revised data on multiferroic LiFeSi2O6. J. Solid State Chem. 2009, 182, 2374–2384. [Google Scholar] [CrossRef]
- Redhammer, G.J.; Senyshyn, A.; Lebernegg, S.; Tippelt, G.; Dachs, E.; Roth, G. A neutron diffraction study of crystal and low-temperature magnetic structures within the (Na,Li) FeGe2O6 pyroxene-type solid solution series. Phys. Chem. Miner. 2017, 44, 669–684. [Google Scholar] [CrossRef]
- Redhammer, G.J.; Senyshyn, A.; Meven, M.; Roth, G.; Prinz, S.; Pachler, A.; Tippelt, G.; Pietzonka, C.; Treutmann, W.; Hoelzel, M. Nuclear and incommensurate magnetic structure of NaFeGe2O6 between 5 K and 298 K and new data on multiferroic NaFeSi2O6. Phys. Chem. Miner. 2011, 38, 139–157. [Google Scholar] [CrossRef]
- Redhammer, G.J.; Tippelt, G. The (Na,Li)FeGe2O6 clinopyroxene-type series: A temperature-dependent single-crystal X-ray diffraction and Fe-57 Mossbauer spectroscopic study. Phys. Chem. Miner. 2016, 43, 1–22. [Google Scholar] [CrossRef]
- Zhang, M.; Redhammer, G.J.; Salje, E.K.H.; Mookherjee, M. LiFeSi2O6 and NaFeSi2O6 at low temperatures: An infrared spectroscopic study. Phys. Chem. Miner. 2002, 29, 609–616. [Google Scholar] [CrossRef]
- Baum, M.; Komarek, A.C.; Holbein, S.; Fernández-Díaz, M.T.; André, G.; Hiess, A.; Sidis, Y.; Steffens, P.; Becker, P.; Bohatý, L.; et al. Magnetic structure and multiferroic coupling in pyroxene NaFeSi2O6. Phys. Rev. B 2015, 91, 214415. [Google Scholar] [CrossRef]
- Baum, M.; Schmalzl, K.; Steffens, P.; Hiess, A.; Regnault, L.P.; Meven, M.; Becker, P.; Bohatý, L.; Braden, M. Controlling toroidal moments by crossed electric and magnetic fields. Phys. Rev. B 2013, 88, 024414. [Google Scholar] [CrossRef]
- Drokina, T.V.; Bayukov, O.A.; Petrakovskii, G.A.; Velikanov, D.A.; Bovina, A.F.; Stepanov, G.N.; Ivanov, D.A. Synthesis and properties of NaFeGe2O6 polycrystals. Phys. Solid State 2008, 50, 2141–2144. [Google Scholar] [CrossRef]
- Drokina, T.V.; Petrakovskii, G.A.; Bayukov, O.A.; Bovina, A.F.; Shimchak, R.; Velikanov, D.A.; Kartashev, A.V.; Volkova, A.L.; Ivanov, D.A.; Stepanov, G.N. Properties of clinopyroxene LiFeGe2O6. Phys. Solid State 2010, 52, 2405–2408. [Google Scholar] [CrossRef]
- Drokina, T.V.; Petrakovskii, G.A.; Keller, L.; Schefer, J.; Balaev, A.D.; Kartashev, A.V.; Ivanov, D.A. Modulated magnetic structure in quasi-one-dimensional clinopyroxene NaFeGe2O6. J. Exp. Theor. Phys. 2011, 112, 121–126. [Google Scholar] [CrossRef]
- Drokina, T.V.; Petrakovskii, G.A.; Molokeev, M.S.; Bondarev, V.S.; Velikanov, D.A. Synthesis and study of structural, thermodynamic, and magnetic properties of NaxLi1-xFeGe2O6 (x = 0.1–0.9) compounds. Phys. Solid State 2016, 58, 1361–1370. [Google Scholar] [CrossRef]
- Drokina, T.V.; Petrakoyskii, G.A.; Molokeev, M.S.; Misyul, S.V.; Bondarev, V.S.; Velikanov, D.A.; Frontzek, M.; Schefer, J. Crystal and magnetic structures, phase transitions in quasi-one-dimensional pyroxenes Na0.5Li0.5FeGe2O6. J. Magn. Magn. Mater. 2015, 385, 243–249. [Google Scholar] [CrossRef]
- Ballet, O.; Coey, J.M.D.; Fillion, G.; Ghose, A.; Hewat, A.; Regnard, J.R. Magnetic order in acmite-NaFeSi2O6. Phys. Chem. Miner. 1989, 16, 672–677. [Google Scholar] [CrossRef]
- Baum, E.; Treutmann, W.; Behruzi, M.; Lottermoser, W.; Amthauer, G. Structural and magnetic properties of the clinopyroxenes NaFeSi2O6 and LiFeSi2O6. Z. Fur Krist. 1988, 183, 273–284. [Google Scholar] [CrossRef]
- Zhou, S.; Zeier, W.G.; Kemei, M.C.; Sougrati, M.T.; Mecklenburg, M.; Melot, B.C. Hydrothermal Preparation and Magnetic Properties of NaFeSi2O6: Nanowires vs Bulk Samples. Inorg. Chem. 2014, 53, 12396–12401. [Google Scholar] [CrossRef]
- Bowen, N.L.; Schairer, J.F.; Willems, H.W.V. The ternary system; Na2SiO3–Fe2O3–SiO2. Am. J. Sci. 1930, 20, 405–455. [Google Scholar] [CrossRef]
- Topas Version 4.1; Bruker AXS Inc.: Madison, WI, USA, 2012.
- Coelho, A. TOPAS and TOPAS-Academic: An optimization program integrating computer algebra and crystallographic objects written in C++. J. Appl. Crystallogr. 2018, 51, 210–218. [Google Scholar] [CrossRef]
- Balzar, D. Voigt-Function Model in Diffraction Line-Broadening Analysis. In Defect and Microstructure Analysis by Diffraction; Snyder, R.L., Fiala, J., Bunge, H.J., Eds.; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Redhammer, G.J.; Roth, G. Structural variations in the aegirine solid-solution series (Na,Li)FeSi2O6 at 298 K and 80 K. Z. Fur Krist. 2002, 217, 63–72. [Google Scholar] [CrossRef]
- Cheary, R.W.; Coelho, A. A fundamental parameters approach to X-ray line-profile fitting. J. Appl. Crystallogr. 1992, 25, 109–121. [Google Scholar] [CrossRef]
- Cheary, R.W.; Coelho, A.A.; Cline, J.P. Fundamental parameters line profile fitting in laboratory diffractometers. J. Res. Natl. Inst. Stand. Technol. 2004, 109, 1–25. [Google Scholar] [CrossRef]
- Lagarec, K.; Rancourt, D.G. Extended Voigt-based analytic lineshape method for determining N-dimensional correlated hyperfine parameter distributions in Mossbauer spectroscopy. Nucl. Instrum. Methods Phys. Res. Sect. B-Beam Interact. Mater. At. 1997, 129, 266–280. [Google Scholar] [CrossRef]
- Rancourt, D.G.; Ping, J.Y. Voigt-based methods for arbitrary-shape static hyperfine parameter distributions in Mossbauer spectroscopy. Nucl. Instrum. Methods Phys. Res. Sect. B-Beam Interact. Mater. At. 1991, 58, 85–97. [Google Scholar] [CrossRef]
- Rietveld, H.M. A profile refinement method for nuclear and magnetic studies. J. Appl. Crystallogr. 1969, 2, 65–71. [Google Scholar] [CrossRef]
- Balzar, D.; Popa, N.C. Crystallite Size and Residual Strain/Stress Modeling in Rietveld Refinement. In Diffraction Analysis of the Microstructure of Materials; Mittemeijer, E.J., Scardi, P., Eds.; Springer: Berlin, Germany, 2004; pp. 125–145. [Google Scholar]
- Prencipe, M.; Mantovani, L.; Tribaudino, M.; Bersani, D.; Lottici, P.P. The Raman spectrum of diopside: A comparison between ab initio calculated and experimentally measured frequencies. Eur. J. Mineral. 2012, 24, 457–464. [Google Scholar] [CrossRef]
- Prencipe, M. Simulation of vibrational spectra of crystals by ab initio calculations: An invaluable aid in the assignment and interpretation of the Raman signals. The case of jadeite (NaAlSi2O6). J. Raman Spectrosc. 2012, 43, 1567–1569. [Google Scholar] [CrossRef]
- Prencipe, M.; Maschio, L.; Kirtman, B.; Salustro, S.; Erba, A.; Dovesi, R. Raman spectrum of NaAlSi2O6 jadeite. A quantum mechanical simulation. J. Raman Spectrosc. 2014, 45, 703–709. [Google Scholar] [CrossRef]
- Popovic, Z.V.; Konstantinovic, M.J.; Popov, V.N.; Cantarero, A.; Dohcevic-Mitrovic, Z.; Isobe, M.; Ueda, Y. Optical phonons in the NaTiSi2O6 oxide with S = 1/2 spin chains. Phys. Rev. B 2005, 71. [Google Scholar] [CrossRef]
- Stangarone, C.; Tribaudino, M.; Prencipe, M.; Lottici, P.P. Raman modes in Pbca enstatite (Mg2Si2O6): An assignment by quantum mechanical calculation to interpret experimental results. J. Raman Spectrosc. 2016, 47, 1247–1258. [Google Scholar] [CrossRef]
- Wang, A.; Jolliff, B.L.; Haskin, L.A.; Kuebler, K.E.; Viskupic, K.M. Characterization and comparison of structural and compositional features of planetary quadrilateral pyroxenes by Raman spectroscopy. Am. Mineral. 2001, 86, 790–806. [Google Scholar] [CrossRef]
- Lambruschi, E.; Aliatis, I.; Mantovani, L.; Tribaudino, M.; Bersani, D.; Redhammer, G.J.; Lottici, P.P. Raman spectroscopy of CaM2+Ge2O6 (M2+ = Mg, Mn, Fe, Co, Ni, Zn) clinopyroxenes. J. Raman Spectrosc. 2015, 46, 586–590. [Google Scholar] [CrossRef]
- Redhammer, G.J.; Ohashi, H.; Roth, G. Single-crystal structure refinement of NaTiSi2O6 clinopyroxene at low temperatures (298 <T <100 K). Acta Crystallogr. Sect. B 2003, 59, 730–746. [Google Scholar] [CrossRef]
- Popovic, Z.S.; Sljivancanin, Z.V.; Vukajlovic, F.R. Sodium pyroxene NaTiSi2O6: Possible haldane spin-1 chain system. Phys. Rev. Lett. 2004, 93, 036401. [Google Scholar] [CrossRef]
- Ohashi, H.; Sekita, M. Raman Spectroscopic Study of the Si–O–Si Stretching Vibration in Clinopyroxenes. J. Jpn. Assoc. Mineral. Petrol. Econ. Geol. 1982, 77, 455–459. [Google Scholar] [CrossRef]











| T (°C) | d (h) | a (Å) | b (Å) | c (Å) | β (°) | Vol. (Å3) | IB (nm) | |
|---|---|---|---|---|---|---|---|---|
| 130 | 196 | 9.739 (3) | 8.806 (3) | 5.3207 (15) | 107.34 (2) | 435.56 | 8.10 (15) | 0.09 (3) |
| 130 | 310 | 9.717 (2) | 8.8034 (19) | 5.3121 (6) | 107.295 (12) | 433.87 | 10.54 (16) | 0.13 (2) |
| 150 | 48 | 9.707 (2) | 8.804 (2) | 5.3135 (11) | 107.305 (15) | 433.54 | 9.66 (16) | 0.130 (18) |
| 150 | 72 | 9.7033 (18) | 8.8017 (19) | 5.3124 (9) | 107.303 (11) | 433.18 | 11.9 (2) | 0.134 (12) |
| 150 | 96 | 9.7018 (18) | 8.8027 (18) | 5.3110 (9) | 107.309 (12) | 433.04 | 12.3 (2) | 0.132 (13) |
| 150 | 120 | 9.7004 (13) | 8.8026 (13) | 5.3105 (7) | 107.305 (8) | 432.93 | 13.41 (17) | 0.129 (9) |
| 150 | 168 | 9.6957 (13) | 8.7996 (13) | 5.3083 (6) | 107.322 (8) | 432.35 | 15.0 (2) | 0.120 (9) |
| 155 | 24 | 9.701 (3) | 8.804 (2) | 5.3131 (11) | 107.287 (15) | 433.24 | 9.14 (14) | 0.127 (19) |
| 160 | 24 | 9.697 (2) | 8.8026 (19) | 5.3111 (10) | 107.293 (13) | 432.86 | 10.16 (14) | 0.129 (15) |
| 170 | 24 | 9.6948 (16) | 8.8022 (15) | 5.3098 (7) | 107,313 (9) | 432.59 | 13.2 (2) | 0.129 (9) |
| 180 | 24 | 9.6893 (12) | 8.8010 (12) | 5.3083 (6) | 107.328 (7) | 432.12 | 15.24 (18) | 0.125 (8) |
| 190 | 24 | 9.6870 (10) | 8.7999 (10) | 5.3068 (5) | 107.345 (6) | 431.81 | 18.1 (2) | 0.115 (6) |
| 200 | 24 | 9.6817 (9) | 8.8018 (9) | 5.3052 (4) | 107.356 (4) | 431.51 | 20.3 (3) | 0.115 (7) |
| 210 | 24 | 9.6804 (9) | 8.8003 (9) | 5.3044 (5) | 107.362 (5) | 431.29 | 22.5 (3) | 0.118 (5) |
| 215 | 24 | 9.6804 (8) | 8.8012 (8) | 5.3040 (4) | 107.367 (5) | 431.30 | 24.0 (3) | 0.101 (5) |
| 220 | 24 | 9.6789 (9) | 8.8011 (9) | 5.3036 (4) | 107.371 (6) | 431.18 | 25.8 (4) | 0.108 (5) |
| 225 | 24 | 9.6787 (7) | 8.8007 (7) | 5.3038 (3) | 107.372 (4) | 431.17 | 27.4 (3) | 0.118 (4) |
| 230 | 24 | 9.6769 (7) | 8.8004 (7) | 5.3036 (3) | 107.377 (4) | 431.04 | 28.1 (3) | 0.101 (4) |
| Sample from 200 °C/24 h annealed at: | ||||||||
| 300 | 24 | 9.6729 (10) | 8.7988 (10) | 5.3025 (5) | 107.401 (6) | 430.65 | 19.9 (3) | 0.112 (6) |
| 400 | 24 | 9.6663 (11) | 8.7978 (11) | 5.3007 (5) | 107.416 (7) | 430.13 | 20.2 (3) | 0.116 (6) |
| 500 | 24 | 9.6623 (9) | 8.7981 (9) | 5.2980 (5) | 107.421 (6) | 429.72 | 20.0 (2) | 0.115 (5) |
| 550 | 24 | 9.6608 (9) | 8.7981 (9) | 5.2971 (4) | 107.421 (5) | 429.58 | 20.0 (3) | 0.115 (6) |
| 600 | 24 | 9.6576 (10) | 8.7966 (11) | 5.2963 (5) | 107.418 (7) | 429.31 | 20.0 (3) | 0.121 (6) |
| 650 | 24 | 9.6563 (19 | 8.7978 (10) | 5.2964 (5) | 107.419 (6) | 429.32 | 20.8 (3) | 0.120 (6) |
| 700 | 24 | 9.6570 (13) | 8.7975 (14) | 5.2956 (6) | 107.428 (8) | 429.24 | 20.9 (4) | 0.121 (7) |
| 750 | 24 | 9.6571 (8) | 8.7979 (8) | 5.2955 (4) | 107.424 (6) | 429.28 | 28.7 (4) | 0.115 (4) |
| 800 | 24 | 9.6569 (5) | 8.7977 (5) | 5.2961 (3) | 107.427 (3) | 429.29 | 38.0 (4) | 0.083 (3) |
| 850 | 24 | 9.6573 (3) | 8.7974 (3) | 5.2952 (5) | 107.426 (2) | 429.26 | 64.6 (7) | 0.044 (4) |
| 900 | 24 | 9.6566 (2) | 8.7977 (2) | 5,2947 (1) | 107.424 (15) | 429.18 | 92 (1) | 0.015 (3) |
| Sample | IS (mm/s) | QS (mm/s) | FWHM (mm/s) | Area (%) | Site | Red. χ2 |
|---|---|---|---|---|---|---|
| 200 °C_T 900 °C | 0.393 (3) | 0.284 (2) | 0.227 (3) | 100 | [6]Fe3+ | 1.372 |
| 200 °C-24 h | 0.395 (2) | 0.357 (2) | 0.262 (3) | 100 | [6]Fe3+ | 1.102 |
| 180 °C-24 h | 0.3946 (19) | 0.378 (2) | 0.260 (4) | 97.9 (6) | [6]Fe3+ | 1.040 |
| 0.194 (8) | 1.055 (7) | 0.264 (6) | 2.1 (6) | [4]Fe3+ | ||
| 170 °C-24 h | 0.396 (3) | 0.414 (2) | 0.271 (7) | 94.7 (8) | [6]Fe3+ | 1.551 |
| 0.181 (4) | 0.946 (6) | 0.273 (6) | 5.3 (8) | [4]Fe3+ | ||
| 160 °C-24 h | 0.395 (2) | 0.428 (2) | 0.274 (4) | 94 (2) | [6]Fe3+ | 1.478 |
| 0.185 (4) | 1.000 (5) | 0.281 (5) | 6 (2) | [4]Fe3+ | ||
| 150 °C-24 h | 0.356 (6) | 0.659 (8) | 0.36 (2) | 100 | [6]Fe3+ | 0.953 |
| 180 °C-24 h | 225 °C-24 h | 200 °C_T 900 °C | NaTiSi2O6 § | Possible Band Assignment & | |
|---|---|---|---|---|---|
| calc. | obs. | Adopted from [43] | |||
| - | - | - | 111 | - | Na-vibrations, SiO4 tilt, bend |
| 130.4 | 131.9 | 132.9 | 147 | 150.8 | Na-vibrations, SiO4 tilt, bend |
| 158.6 | 159.0 | 159.8 | 165 | 176.6 | Na-vibration //z |
| 178.1 | 178.5 | 178.7 | 184 | 188.8 | Na-vibrations, SiO4 and FeO6 bend |
| 190.0 | 190.7 | 191.6 | 195 | 208.6 | Obr–Si–Obr bending |
| 210.5 | 211.3 | 212.0 | 212 | 220.8 | Na-vibrations, SiO4 and FeO6 bend |
| 262.3 | 262.7 | 263.2 | 250 | 266.5 | Na-vibration, O–Fe–O bend |
| 272.9 | 273.9 | 275.0 | 272 | 275.4 | Na-vibration, O–Si–O bend |
| 290.8 | 291.5 | 292.2 | 282 | 304.4 | Na- and FeO6 vibration |
| 305.9 | 307.6 | 309.1 | 307 | - | SiO4 tilt, bend, Fe vibration |
| 336.4 | 338.0 | 339.2 | 309 | 329.3 | SiO4 tilt, O–Fe–O bend |
| 345.0 | 345.2 | 345.4 | 352 | - | SiO4 tilt |
| 364.4 | 365.5 | 366.6 | 362 | 388.0 | O–Fe–O bend |
| 382.4 | 382.9 | 383.4 | 452 | - | O–Fe–O bend |
| 460.8 | 462.6 | 462.7 | 466 | 468.2 | O–Fe–O bend |
| 494.6 | 495.3 | 496.2 | 487 | 494.3 | O–Si–O bend |
| 528.5 | 528.7 | 528.9 | 537 | - | O–Fe–O bend |
| 541.4 | 541.7 | 541.9 | 543 | 553.6 | O–Fe–O, O–Si–O bend |
| 558.5 | 559.2 | 560.1 | 574 | - | O–Si–O bending |
| - | - | - | 627 | 624.2 | Si–Onbr, Ti–O stretching |
| 675.0 | 675.0 | 676.7 | 693 | 673.3 | Si–Obr stretching // x; Si–Obr–Si bend |
| 755.4 | 756.5 | 757.9 | 748 | 750.0 | Si–Obr stretching // x |
| 804.1 | 805.0 | 804.9 | 821 | 837.6 | Si–Obr stretching // yz |
| 864.4 | 864.9 | 865.3 | 870 | - | Si–Obr stretching // yz |
| - | - | - | 908 | - | Si–Onbr stretching |
| 947.1 | 947.9 | 948.7 | 950 | 947.6 | Si–Onbr stretching |
| 959.6 | 959.6 | 959.7 | 958 | - | Si–Onbr stretching |
| 970.9 | 971.6 | 971.6 | 968 | 693.7 | Si–Onbr stretching, asym. |
| 972.8 | 998.8 | 1014.2 | 1017 | 1023.6 | Si–O4, TiO4 breathing |
| 1041.2 | 1042.0 | 1042.1 | 1047 | 1038 | Si–Onbr stretching, asym. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Redhammer, G.J.; Weber, J.; Tippelt, G.; Zickler, G.A.; Reyer, A. Low Temperature Synthesis of Aegirine NaFeSi2O6: Spectroscopy (57Fe Mössbauer, Raman) and Size/Strain Analysis from X-ray Powder Diffraction. Minerals 2019, 9, 444. https://doi.org/10.3390/min9070444
Redhammer GJ, Weber J, Tippelt G, Zickler GA, Reyer A. Low Temperature Synthesis of Aegirine NaFeSi2O6: Spectroscopy (57Fe Mössbauer, Raman) and Size/Strain Analysis from X-ray Powder Diffraction. Minerals. 2019; 9(7):444. https://doi.org/10.3390/min9070444
Chicago/Turabian StyleRedhammer, Günther J., Julian Weber, Gerold Tippelt, Gregor A. Zickler, and Andreas Reyer. 2019. "Low Temperature Synthesis of Aegirine NaFeSi2O6: Spectroscopy (57Fe Mössbauer, Raman) and Size/Strain Analysis from X-ray Powder Diffraction" Minerals 9, no. 7: 444. https://doi.org/10.3390/min9070444
APA StyleRedhammer, G. J., Weber, J., Tippelt, G., Zickler, G. A., & Reyer, A. (2019). Low Temperature Synthesis of Aegirine NaFeSi2O6: Spectroscopy (57Fe Mössbauer, Raman) and Size/Strain Analysis from X-ray Powder Diffraction. Minerals, 9(7), 444. https://doi.org/10.3390/min9070444