Performance Evaluation of Bidding-Based Multi-Agent Scheduling Algorithms for Manufacturing Systems

Abstract

Artificial Intelligence techniques have being applied to many problems in manufacturing systems in recent years. In the specific field of manufacturing scheduling many studies have been published trying to cope with the complexity of the manufacturing environment. One of the most utilized approaches is (multi) agent-based scheduling. Nevertheless, despite the large list of studies reported in this field, there is no resource or scientific study on the performance measure of this type of approach under very common and critical execution situations. This paper focuses on multi-agent systems (MAS) based algorithms for task allocation, particularly in manufacturing applications. The goal is to provide a mechanism to measure the performance of agent-based scheduling approaches for manufacturing systems under key critical situations such as: dynamic environment, rescheduling, and priority change. With this mechanism it will be possible to simulate critical situations and to stress the system in order to measure the performance of a given agent-based scheduling method. The proposed mechanism is a pioneering approach for performance evaluation of bidding-based MAS approaches for manufacturing scheduling. The proposed method and evaluation methodology can be used to run tests in different manufacturing floors since it is independent of the workshop configuration. Moreover, the evaluation results presented in this paper show the key factors and scenarios that most affect the market-like MAS approaches for manufacturing scheduling.

1. Introduction

The manufacturers’ success is no longer measured by their ability to cost-effectively produce a single product; success now seems to be measured in terms of flexibility, agility, and versatility [1]. In order to survive, manufacturing systems need to adapt at an ever-increasing pace to incorporate new technology, new products, new organizational structures, etc.

The above trends have motivated researchers in academia and industry to create and exploit new production paradigms on the basis of autonomy and co-operation because both concepts are necessary to create flexible behavior and thus to adapt to the changing production conditions. Such technologies provide a natural way to overcome such problems and to design and implement distributed intelligent manufacturing environments [1,2]. One of the complex problems in manufacturing systems is scheduling. Manufacturing scheduling is the process of assigning manufacturing resources over time to the set of manufacturing processes in the process plan. It determines the most appropriate time to execute each operation, taking into account the temporal relationships between manufacturing processes and the capacity limitations of the shared manufacturing resources. The assignments also affect the optimality of a schedule with respect to criteria such as cost, tardiness, or throughput. In summary, scheduling is an optimization process where limited resources are allocated over time among both parallel and sequential activities. Such an optimization process is becoming increasingly important for manufacturing enterprises to increase their productivity and profitability through greater shop floor agility to survive in a globally competitive market [3].

In the past twenty years, researchers have been applying Artificial Intelligence (AI) techniques to many problems [4,5,6,7]. For a large literature review of AI applications for manufacturing systems see [8]. In the specific field of manufacturing scheduling many works are published that try to cope with the complexity of the manufacturing environment. One of the approaches most utilized in the specialized literature is (multi)agent-based scheduling. Nevertheless, despite the large list of studies reported in this field there is almost no resource or scientific study on the performance measure of this type of approaches under very common and critical execution situations. Even so, Bench4Start [9] must be pointed out as an interesting approach to define benchmarking solutions for manufacturing systems. Nevertheless, Bench4Start does not take into account multi-agent based approaches for manufacturing scheduling. The goal of the work presented in this paper is to provide a mechanism to measure the performance of agent-based scheduling approaches for manufacturing systems under key critical situations such as: dynamic environment, rescheduling, and priority change. With this mechanism it will be possible to simulate critical situations and to stress the system in order to measure a given agent-based scheduling method performance. In this work a specific method developed for bidding-based or market-like multi-agent approaches of manufacturing scheduling is presented.

2. Task Allocation in Intelligent Manufacturing Systems: State of the Art, Background

Techniques from Artificial Intelligence have already been used in Intelligent Manufacturing for more than twenty years [1]. However, the recent developments in multi-agent systems in the domain of Distributed Artificial Intelligence have brought new and interesting possibilities. Distributed intelligent manufacturing systems are based on multi-agent system (MAS) technology [11]. MAS studies the coordination of intelligent behavior among a group of (possibly preexisting) agents. An agent is an autonomous and flexible computational system, which is able to act in the environment [11]. Today MAS is a very active area of research, which is beginning to see commercial and industrial applications [12,8,10,13].

The scheduling problem exists not only in manufacturing enterprises, but also in organizations like publishing houses, universities, hospitals, airports, and transportation companies. It is typically NP-hard, i.e., it is impossible to find an optimal solution without the use of an essentially enumerative algorithm, with computation time increasing exponentially with problem size. However, the manufacturing scheduling problem is one of the most difficult of all scheduling problems.

A well-known manufacturing-scheduling problem is the classical job shop scheduling where a set of jobs and a set of machines are given. Each machine can handle at most one job at a time. Each job consists of a chain of operations, each of which needs to be processed during an uninterrupted time period of a given length on a given machine. The purpose is to find the best schedule, i.e., an allocation of the operations to time intervals on the machines, which has the minimum total duration required completing all jobs. The total number of possible solutions for a classical job-shop scheduling problem with n jobs and m machines is (n!)m.

The problem becomes even more complex when unforeseen dynamic situations are considered. In a job shop manufacturing environment, things rarely go as expected. The system may be asked to include additional tasks that are not anticipated, or to adapt to changes to several tasks, or to neglect certain tasks. The resources available for performing tasks are subject to changes. Certain resources can become unavailable, and additional resources can be introduced. The beginning time and the processing time of a task are also subject to variations. A task can take more or less time than anticipated, and tasks can arrive early or late. Other uncertainties include power system failures, machine failures, operator absence, and unavailability of tools and materials. An optimal schedule, generated after considerable effort, may rapidly become unacceptable because of unforeseen dynamic situations on the shop floor and a new schedule may have to be generated. This kind of rescheduling problem is also called dynamic scheduling or real-time scheduling.

Agent-Based Scheduling for Manufacturing

In this paper the discussion on scheduling is restricted to (a) the allocation of production operations to specific resources and (b) the specification of timing (start, duration, and completion) for those operations. The key characteristics, which typify an intelligent manufacturing scheduling approach, are [14]:

−

A local decision-making and computational capability associated with each agent.

−

A cooperative interaction strategy that governs the way in which agents exchange information and determine mutually acceptable solutions.

−

An interchange mechanism or protocol, which manages the exchange of message types, needed to execute the cooperative strategy.

−

A means of ensuring that the global concerns of the factory are addressed.

−

A degree of central coordination (not present in all solutions).

Work on agent-based scheduling for manufacturing systems to date has predominantly experimented with different algorithms [15,16,17,18,19,20,21] and simulated testing although issues such as the desire for an emergent schedule vs. a fixed schedule structure, and the relationship between scheduling and execution has been examined also. Schiegg [22] compiled an extensive bibliography on multi-agent scheduling in manufacturing systems.

In agent-based manufacturing process planning and scheduling systems, bidding-based negotiations or market-like approaches are commonly used. In systems of this kind, the applied agent negotiation protocols require individual agents to reply to the incoming offers, to compete, and to negotiate or to bargain with other agents. As a result, rich knowledge bases and powerful learning and reasoning mechanisms are very important. Each agent should have at least knowledge of the capability, availability, and cost of the physical resource (e.g., a machine) represented by it. Some sophisticated agents need to have knowledge of other agents in the system, the products to be manufactured, and the know-how (historical experience, successful cases), etc.

The decision scheme of an individual agent depends primarily on two aspects [3]: coordination or negotiation mechanisms used by the multi-agent system and its local decision-making mechanisms based on knowledge. For example, a Contract Net protocol needs each individual agent to reply to an offer with requested information such as cost, starting time, processing time, etc. [23]. A game-theory-based multi-agent system needs agents to follow game rules [24]. While a multi-agent system implemented with a conversation scheme will need each agent to follow the conversation policies [25]. Local decision-making may use rule-based and case-based mechanisms reasoning on top of the knowledge the agent possesses. To update an agent’s knowledge, learning mechanisms are needed. Such learning mechanisms may range from case-based reasoning to neural network and fuzzy logic-based reasoning.

Negotiation protocols are used in most agent-based manufacturing scheduling systems for resource allocation. The Contract Net Protocol or its modified versions are the most commonly utilized, although some other protocols such as the voting mechanism have also been considered. Although Contract Net and its variants are usually used as negotiation protocols in most agent-based scheduling systems, market-based approaches are becoming more and more popular. Market-based like protocols use the so-called bargaining process or auction process, which is also simple and easy to use. Market-based like approaches have recently been used in a number of agent-based scheduling systems [26,27,28,29].

Two types of agent-based distributed manufacturing scheduling systems can be distinguished according to the following characteristics.

• Scheduling is an incremental search process that can involve backtracking. Agents, responsible for scheduling orders, perform local incremental searches for their orders and may consider multiple resources. The global schedule is obtained through the merging of local schedules. This is very similar to centralized scheduling.
• An agent represents a single resource (e.g., a work cell, a machine, a tool, a fixture, a worker, etc.) and is responsible for scheduling this resource. This agent may negotiate with other agents to carry out the overall scheduling [27,28,30].

Most agent-based manufacturing scheduling systems proposed and developed in literature use the second approach.

The work presented in this paper is focused on the second approach for the following potential advantages. (I) Resource agents may be connected directly to physical devices they represented so as to realize real-time dynamic rescheduling (of course, not immediate rescheduling after any change in the working environment for the sake of system stability). It may therefore provide the manufacturing system with higher reliability and device fault tolerance. (II) Schedules are achieved by using mechanisms similar to those being used in manufacturing supply chains (i.e., negotiation rather than search). This way, the manufacturing capabilities of manufacturers can be directly connected to each other and optimization is possible at the supply chain level in addition to the shop floor level and the enterprise level.

It is becoming clear that agent-based approaches offer many advantages for distributed manufacturing scheduling systems: modularity, reconfigurability, scalability, upgradeability, and robustness (including fault recovery). The results achieved so far in the agent research community provide excellent motivation for further development of solutions in this area. Moreover, at present, there are no other ways to solve these complex problems. However, whether the potential advantages of agent-based approaches can actually be realized in industrial systems will depend on the selection of a suitable system architecture for agent organization and an appropriate approach for agent encapsulation; on the design and implementation of effective mechanisms and protocols for communication, cooperation, coordination, and negotiation; and on the design and implementation of advanced internal architectures and efficient decision schemes of individual agents. Moreover, the key to success in any field is how well a given approach performs under very common and critical situations. Our goal is to assess this problem providing a mechanism that can help when evaluating the performance of a given agent-based scheduling approach for manufacturing.

3. A Bidding-Based MAS Approach for Dynamic Scheduling in Manufacturing

In this work the main interest is the performance of bidding-based or market-like MAS approaches for dynamic scheduling of manufacturing systems under critical situations.

The bidding process implemented into a MAS is any protocol that allows an agent to focus on one or more resources to determine its final allocation as well as the involved transactions set in which the agents will be involved.

The bidding scheme has proven its efficiency as a general solution when applied to resource allocation integrated into a MAS [31]. Many variants of biddings have been developed, including single, combined, and multiple [32].

It is important to remark that the most common bidding scheme—ascendant bidding, known as English auction—represents just a small piece of a wide bidding spectrum. The fact that the bidding process is a relatively simple resource allocation mechanism, allows this working scheme to conform an infinite set.

The most common bidding model includes: one resource to be allocated, one seller, and many potential buyers. Each one of the buyers will set their own tag price for the item and want to acquire it at the lowest price as well.

Having multiple agents grouped at one side of the market environment makes them fall into the single-sided bidding category. The main goal defined for this classification is developing a specific protocol in order to solve a certain amount of defined global criteria, like creating an earn maximizing protocol, or establishing an economically efficient auction process, one that guarantees the potential buyer to acquire the selling item offering the maximum market value.

As previously stated, there is a wide range of working schemes for bidding processes. However, they all share a diverse structure, taxonomically speaking, common to all of them. For research purposes and simulation of real applications, they are to be considered as a structured framework for diverse negotiation threads. Each one of them includes certain rules, basically outlined by three main categories:

(1)

Postulation rules: defining how, who, when, and what is to be contained for every auction bid.

(2)

Clarification rules: defining when negotiations occur, what each one of them is related to in the bidding process (who obtains the resources and which bids are being modified)

(3)

Information rules: related to bidders with active participation in the bidding process

The vast majority of the different bidding schemata include the above rules to a certain degree. However, more rules are likely to be added. However, aside from the bidding type and complexity aggregated to the industrial process, each design includes those three basic axes in its different implementations.

Given the vast amount of bidding schemes, the problem of how to select one of them may arise. With some considerations, the selection is not that relevant, as formalized in the following theorem:

Theorem 1. Revenue Equivalence Theorem. [33] Assume that each of n risk-neutral agents has an independent private valuation for a single good at auction, drawn from a common cumulative distribution F(o) that is strictly increasing and atom less on [o, ō]. Then any auction mechanism in which the good will be allocated to the agent with the highest valuation, and any agent with valuation o has an expected utility of zero; this yields the same expected revenue, and, hence, results in any bidder with valuation o making the same expected payment.

From the above paragraph, it can be concluded that when bidders have independent and private bids, every auction scheme earns an equivalent. Aside from the theorem being useful to remark that the bidding type selection is not that relevant, it is a very useful analytical tool. In particular, it can be used to identify equilibrium strategies in that auction types fulfill the theorem conditions.

4. The Proposed Model and Working Environment

In this section the mechanism to measure the performance of bidding-based scheduling approaches for manufacturing systems is presented. It is defined as a MAS that can simulate critical situations in order to stress a manufacturing working environment and measure the performance of the scheduling approach (bidding-based) that is being used. It is important to point out that the work presented in this paper is focused on bidding-based mechanisms, nevertheless, other approaches for agent-based manufacturing scheduling are also important. The model described in this section can be modified in order to cope with other agent-based approaches. The final goal of the work, which is being developed by the authors, is to provide a complete package that the user can configure in order to test different agent-based approaches for manufacturing systems.

The proposed MAS architecture includes two levels. The first one is composed of those entities related to the real environment to be simulated. The second comprehends the responsible agents designed for controlling and handling the aforementioned entities. Furthermore, the MAS architecture requires more elements, such as information and communication management for each agent, as well as coordination and execution control for the assigned jobs.

The working environment in which the proposed approach will be tested consists of an assembly line system, with job stations receiving constant manufacturing assignments from different categories. The integrated agents are autonomous, each one representing a physical entity into the system.

To properly apply the bidding scheme, two agent categories are included: bidder and auctioneer agents, both autonomous and able to intercommunicate:

Auctioneer agent: coordinates the initial stage of the auction process. It sets the starting price of the job order. Moreover, it analyzes the generated bids and defines the best one.

Bidder agent: encapsulates the state of a given machine when a job order arrives. It also defines the bid during the entire process of the auction.

The implemented auction technique is the English auction. The auctioneer sets the assigned value for the job order as well as the prices randomly generated and offered by the bidder agents. The auctioneer agent generates and sends the reserved price for the resource to the system. A bidding agent is assigned for each assembly line. The individual bids are sequentially sent to the auctioneer when a new job unit requires processing.

In the following sections, a complete and detailed evaluation of the bidding-based MAS approach for task allocation in manufacturing environment is presented. The bidding-based approach is tested in order to measure its performance under key critical requirements of manufacturing systems. In order to simulate the situations for testing, dynamic environment and rescheduling, specific algorithms, which include these characteristics, are proposed. It is important to point out that if the concrete bidding mechanisms needs to be changed (for example, a Dutch auction, Japanese auction, etc.) it is only required to change the step in which the auctioneer evaluates the bids and the internal process by which every bidder agent defines their individual bid.

4.1. Dynamic Environment

One of the basic properties characterizing a modern manufacturing system is dynamism, defined as the set of changes in the structure and behavior during operation. This expresses different competencies, responsibilities, and relationships between entities [34].

The first scheduling requirement in the manufacturing field is for it to be dynamic [35]; in it, the job orders arrive at the assembly line with diverse characteristics like different priorities, manufacturing times, etc. In order to create a simulation environment for this requirement, the software elements depicted in Figure 1 were included.

Figure 1. Conceptual classes for the multi-agent systems (MAS) Dynamic Environment.

Figure 1. Conceptual classes for the multi-agent systems (MAS) Dynamic Environment.

For the proper execution of the Dynamic Environment simulation tests, the following conditions were considered:

−

Every agent can process only one job at a time.

−

A set of n operation jobs is available for processing at time zero.

−

Setup times for the operations are included in processing times.

−

m different machines are continuously available.

−

The evaluations for the bids, resource value assignations, and bid amount generations are effectuated randomly.

−

The priority values are randomly generated for every job order and classified as being of high, medium or low priority. Unless otherwise stated, the corresponding range values for all simulations are 0–3 for low, 4–7 for medium and 8–9 for high priorities, respectively.

−

Parameters evaluated: Allocation or rejection (when the maximum bid value is lower than the resource value), time for each resource, job order priority and occurrence of assignation with increased initial value

The operation flow related to the MAS agents for this test is in Table 1.

Table 1. Algorithm for job allocation in the Dynamic Environment test.

(1) The auctioneer agent Si sets the initial value Vi for the corresponding resource to every generated job assignment. (2) Every registered bidder agent Aj presents one bid (ρj), constituting a set of eligible random options Cij = {ρj, ρj+1 … ρj+n} to allocate every job. Si verifies every bid and once ρj ≥ Vi is accomplished; the corresponding resource is assigned to the Aj agent. (3) ρj ≥ Vi + 1 is evaluated, in order to maximize the allocation value of the corresponding resource. If the evaluation is valid, the resource will be allocated at Vi + 1 price, otherwise the allocation will take effect at Vi price. (4) If ρj < Vi is valid for every element of Cij, the allocation will be considered empty. A new bidding stage takes effect. (5) If ρj = … ρj+1 = ρj+n is valid for every member of Cij, ρj will be considered the maximum bid for the corresponding resource allocation.

Table 1. Algorithm for job allocation in the Dynamic Environment test.

(1) The auctioneer agent Si sets the initial value Vi for the corresponding resource to every generated job assignment. (2) Every registered bidder agent Aj presents one bid (ρj), constituting a set of eligible random options Cij = {ρj, ρj+1 … ρj+n} to allocate every job. Si verifies every bid and once ρj ≥ Vi is accomplished; the corresponding resource is assigned to the Aj agent. (3) ρj ≥ Vi + 1 is evaluated, in order to maximize the allocation value of the corresponding resource. If the evaluation is valid, the resource will be allocated at Vi + 1 price, otherwise the allocation will take effect at Vi price. (4) If ρj < Vi is valid for every element of Cij, the allocation will be considered empty. A new bidding stage takes effect. (5) If ρj = … ρj+1 = ρj+n is valid for every member of Cij, ρj will be considered the maximum bid for the corresponding resource allocation.

4.2. Rescheduling

The Rescheduling process can be defined in general terms as a dynamic adjustment that updates the production scheme in response to sudden interruptions susceptible to occurrence in the manufacturing shop floor. There are diverse strategies that specify how and when to apply rescheduling to properly confront those occurrences. Within the scope of this work, the following strategies will be considered: High Priority and High Utilization [36].

The above strategies represent the combination of two elements: Rescheduling criteria and types of used algorithm for production rescheduling, both described in the following paragraph.

Rescheduling criteria: An interrupted job order by a failure in the manufacturing machines will be referenced as affected job; also, the amount of time for job completion will be the remaining time.

• Job priority: This criterion refers to the case of alternative machine susceptible of accepting the affected job, depending upon the priorities of the assigned job (actual job priority > minimum alternative job priority). If the affected job priority is higher than the equivalent in the processing job in the alternative machine, the latter is interrupted and the affected job starts to be processed.
• Machine utilization: Referred to when there are alternative machines able to receive the affected job depending upon its amount of utilization. When a failure in the machine affects a job, the availability of the alternatives is evaluated. If many options are presented, the machine with the lowest workload is selected.

Algorithm types

• High interference: Applied when a failure occurs. When activated, this algorithm will search alternative processing machines, ignoring the remaining time of the affected job process.
• Low interference: Consists of searching alternative machines only when failure time is higher than the affected job process remaining time.

In order to apply this test to the proposed algorithm, a set of software components was developed, as depicted in Figure 2.

Figure 2. Conceptual classes for rescheduling.

Figure 2. Conceptual classes for rescheduling.

In the following sections, the two types of simulated situations for rescheduling are implemented by the High Priority Algorithm and the High Utilization Algorithm. In this way the performance of the bidding-based MAS approach for scheduling can be validated when using the two mentioned techniques.

4.2.1. High Priority Algorithm

For simulation purposes of rescheduling requirements, the bidding-based algorithm is modified in order to use the high priority technique. In the first instance, when there is a breakdown occurrence affecting any of the scheduled jobs, the algorithm will select an alternative machine. If the priority of the affected job is higher than the available capacity of the remaining machines, the allocation is considered deserted. Otherwise, the job will be allocated to the machine with enough processing capacity.

In this test, the following conditions are considered:

• Every agent can process only one job at a time
• The random breakdown occurrence will always be applied on the machine with the best available capacity, 0 being for no machine failure and 1 for absence of breakdown. After the revision of this value for every scheduled job, the allocation process is initiated.
• A set of n operation jobs is available for processing at time zero.
• Setup times for the operations are included in processing times.
• m different machines are continuously available.

The characteristics of the High Priority Algorithm are defined in Table 2.

Table 2. High priority algorithm for rescheduling.

(1) The auctioneer agent Si sets the starting price (priority) Vi corresponding to every job order generated. Operation time ti is initialized. (2) Every registered bidding agent Aj offers a particular bid ρj, structuring one eligible random options set Cij = {ρj, ρj+1 … ρj+n} for assigning each job order. Si verifies every bid and evaluates ρj ≥ Vi, if valid, the resource is allocated to the Aj corresponding agent. (3) A failure condition is generated randomly in the maximum bid agent max (ρj). As an alternative, the agent with the immediate lower bid is selected. The operation time increases due to the failure. The increment is defined by: ti = ti + ∆ti. (4) ρj ≥ Vi + 1, is evaluated in order to maximize the allocation value of the corresponding resource. When valid, the corresponding job will be definitely allocated at a price equal to Vi + 1, otherwise it will be allocated at a price equal to Vi. (5) If ρj < Vi is valid for every element of Cij, the allocation will be considered deserted, and a new round of bids will take place. In a real environment, this is interpreted as a ðt waiting time, equivalent to the reincorporation of the failed machine. (6) If ρj = ρj+1 = … ρj+n is valid for every element of Cij, ρj will be designated as the maximum bid for defining the resource allocation, evaluated for both failure or normal working processes.

Table 2. High priority algorithm for rescheduling.

(1) The auctioneer agent Si sets the starting price (priority) Vi corresponding to every job order generated. Operation time ti is initialized. (2) Every registered bidding agent Aj offers a particular bid ρj, structuring one eligible random options set Cij = {ρj, ρj+1 … ρj+n} for assigning each job order. Si verifies every bid and evaluates ρj ≥ Vi, if valid, the resource is allocated to the Aj corresponding agent. (3) A failure condition is generated randomly in the maximum bid agent max (ρj). As an alternative, the agent with the immediate lower bid is selected. The operation time increases due to the failure. The increment is defined by: ti = ti + ∆ti. (4) ρj ≥ Vi + 1, is evaluated in order to maximize the allocation value of the corresponding resource. When valid, the corresponding job will be definitely allocated at a price equal to Vi + 1, otherwise it will be allocated at a price equal to Vi. (5) If ρj < Vi is valid for every element of Cij, the allocation will be considered deserted, and a new round of bids will take place. In a real environment, this is interpreted as a ðt waiting time, equivalent to the reincorporation of the failed machine. (6) If ρj = ρj+1 = … ρj+n is valid for every element of Cij, ρj will be designated as the maximum bid for defining the resource allocation, evaluated for both failure or normal working processes.

4.2.2. High Utilization Algorithm

This algorithm includes basically the same processing rules as the High Priority Algorithm, with one difference: once the failure in the best machine is generated, a seek process is started in order to find the minimum bid presented in the system (the least capable agent) This algorithm is formalized in Table 3.

4.3. Priority Change Algorithm

The jobs that are under execution in a manufacturing system can experiment priority changes during exection due to different situations, i.e., changes in the raw material bills, new job orders with different priority that enter the system affecting the already scheduled jobs, etc. In order to cope with this situation the Priority Change Algorithm is proposed to manage the system behavior when the priority level associated with the actual job rises at some point during execution. In order to simulate this situation, the proposed approach randomly generates two priority levels for the given job order, and defines a subsystem composed of the most and least occupied agents. Table 4 describes this algorithm in a more detailed fashion.

Table 3. High utilization algorithm for rescheduling.

(1) The auctioneer agent Si assigns the starting price (priority) Vi for the resource corresponding to every job order generated. Operation time ti is initialized. (2) Every registered bidder agent Aj generates a ρj bid, defining a random probable values set Cij = {ρj, ρj+1 … ρj+n} for assigning each job order. Si verifies every bid and evaluates ρj ≥ Vi, when valid, the resource is allocated to the Aj agent temporarily. (3) A failure condition in the agent with the best offer: max (ρj), is generated. As an alternative, the agent accomplishing a min(Cij)—which represents the agent with the most inactive state in the set—is chosen. The total operation time reflects an increment due to the generated failure defined for ti = ti + ∆ti. (4) ρj ≥ Vi + 1 is evaluated, trying to maximize the allocation job value. When the comparison evaluates true, the job will be allocated at a Vi + 1 price tag, otherwise the final assignation price will be Vi. (5) If ρj < Vi is true for every element of Cij, the allocation process is considered deserted. A new bidding round starts. This is considered as a ðt waiting time, equivalent to the reincorporation of the machine including a generated failure. (6) If ρj = ρj+1 = … ρj+n is true for every element of Cij, ρj is designated as the highest bid for defining the resource allocation, and is evaluated for all system configurations.

Table 3. High utilization algorithm for rescheduling.

(1) The auctioneer agent Si assigns the starting price (priority) Vi for the resource corresponding to every job order generated. Operation time ti is initialized. (2) Every registered bidder agent Aj generates a ρj bid, defining a random probable values set Cij = {ρj, ρj+1 … ρj+n} for assigning each job order. Si verifies every bid and evaluates ρj ≥ Vi, when valid, the resource is allocated to the Aj agent temporarily. (3) A failure condition in the agent with the best offer: max (ρj), is generated. As an alternative, the agent accomplishing a min(Cij)—which represents the agent with the most inactive state in the set—is chosen. The total operation time reflects an increment due to the generated failure defined for ti = ti + ∆ti. (4) ρj ≥ Vi + 1 is evaluated, trying to maximize the allocation job value. When the comparison evaluates true, the job will be allocated at a Vi + 1 price tag, otherwise the final assignation price will be Vi. (5) If ρj < Vi is true for every element of Cij, the allocation process is considered deserted. A new bidding round starts. This is considered as a ðt waiting time, equivalent to the reincorporation of the machine including a generated failure. (6) If ρj = ρj+1 = … ρj+n is true for every element of Cij, ρj is designated as the highest bid for defining the resource allocation, and is evaluated for all system configurations.

Table 4. Priority change algorithm.

(1) The auctioneer agent Si assigns the initial prices (priorities) Vi y Hi for the corresponding resource on each generated job. Hi > Vi. is true for all cases (2) From the priority ranges defined, the increment in priority will be classified as low to medium, medium to high or low to high, according to the generated values for Vi y Hi (3) Every registered bidder agent Aj presents a ρj bid, defining a set of random possible options Cij = {ρj, ρj+1 … ρj+n} in order to allocate each job order. Si verifies every bid and makes a selection on the best and worst offers max(ρj) and min(ρj), corresponding to the most and least occupied agents in the system, respectively. (4) K = max(ρj) + min(ρj) is defined as the total capacity for the system to process the job order. (5) If K < Vi evaluates true, the allocation process is considered deserted, and a new bidding round takes place. (6) If K ≥ Vi and K < Hi, the system is considered saturated when trying to process the actual job with a higher priority value. This result is added to the general evaluation of the system. (7) If K ≥ Hi is true, the system is considered not saturated and capable of processing the task at a higher priority. The result of the allocation is registered and incorporated to the general evaluation for the SMA on this specific test.

Table 4. Priority change algorithm.

(1) The auctioneer agent Si assigns the initial prices (priorities) Vi y Hi for the corresponding resource on each generated job. Hi > Vi. is true for all cases (2) From the priority ranges defined, the increment in priority will be classified as low to medium, medium to high or low to high, according to the generated values for Vi y Hi (3) Every registered bidder agent Aj presents a ρj bid, defining a set of random possible options Cij = {ρj, ρj+1 … ρj+n} in order to allocate each job order. Si verifies every bid and makes a selection on the best and worst offers max(ρj) and min(ρj), corresponding to the most and least occupied agents in the system, respectively. (4) K = max(ρj) + min(ρj) is defined as the total capacity for the system to process the job order. (5) If K < Vi evaluates true, the allocation process is considered deserted, and a new bidding round takes place. (6) If K ≥ Vi and K < Hi, the system is considered saturated when trying to process the actual job with a higher priority value. This result is added to the general evaluation of the system. (7) If K ≥ Hi is true, the system is considered not saturated and capable of processing the task at a higher priority. The result of the allocation is registered and incorporated to the general evaluation for the SMA on this specific test.

5. Performance Evaluation of the Bidding-Based Scheduling Approach Using the Proposed Mechanism

In this section the analysis of the execution of the bidding-based MAS approach for task allocation is described. The test where executed taking into account the performance criteria defined and modeled in the previous section: dynamic environment, rescheduling with high priority, rescheduling with high utilization, and priority change. The tests were executed running 100 simulations for the working environment (defined in Section 5) under the different complexity scenarios.

5.1. Dynamic Environment Test

The dynamic environment test was executed simulating the dynamic and random entrance of new job orders for one to 10 tasks. Moreover, every task was randomly labeled with a priority value: eight to nine for high priority, four to seven for medium priority, and zero to three for low priority. The results depicted in Figure 3 show that high priority allocation for jobs decreases when there are more job orders in the system. It varies, on average, from 24% with one job to 10% with ten jobs. On the other hand, the number of jobs does has almost no effect on the allocation of medium priority jobs in the system.

Finally, it can be noticed that when the number of jobs in the system increases, a very high amount of allocated jobs belongs to the low priority level, reaching up to 51.5% on average. Also, the unallocated job index with one job is very high (39%), while it remains almost stable (10.5% on average) when the number of jobs increases.

Figure 3. Dynamic Environment Test: Task allocation for one to 10 tasks order with high, medium, and low priority.

Figure 3. Dynamic Environment Test: Task allocation for one to 10 tasks order with high, medium, and low priority.

5.2. Rescheduling with High Priority Test

The rescheduling with High Priority test was executed with the following configuration: One hundred simulations; dynamic entrance of new job orders for one to 10 tasks, and priority values of eight to nine meaning high priority tasks, four to seven for medium, and zero to three for low. Random breakdown occurrences are simulated. The breakdown is always applied to the machine with the best available capacity, with zero being for no machine failure and one for absence of breakdown. After the revision of this value for every scheduled job, the allocation process is initiated.

Figure 4 shows that, despite the random failure generation in the most capable machine, the unassigned job levels maintain a low average for the medium and low priority scenarios. Although the high priority level scenario shows a decreasing performance when more job orders appear in the system, the percentage of allocated tasks is always between 30% and 50%. This result, in a real working environment scenario, indicates that the system is capable of processing a high percentage of jobs with a level of priority higher than the one initially required.

Figure 4. Rescheduling with High Priority Test: Task allocation for one to three task orders with high, medium, and low priority.

Figure 4. Rescheduling with High Priority Test: Task allocation for one to three task orders with high, medium, and low priority.

Once the testing process of the described software model finishes, having two generated job tasks, the unallocation index grows noticeably, moving from 9% to 20% for medium priority, and from 15% to 35% for high priority. This characteristic remains practically the same for low priorities. Despite that, the system behavior maintains acceptable levels of completed jobs, given that the unallocated job average level is lower than 10%. The observed general distribution is 25%, 30%, and 44% for high, medium, and low priority levels, respectively. The average completion time (50 ms) is slightly higher than the one observed in the previous test scenario (Dynamic Environment). This implies that the decision process before a machine failure generates an additional delay in the general allocation time.

5.3. Rescheduling with High Utilization Test

This test was executed under the same configuration of the working environment as for the previous tests (that is, 100 simulations; dynamic and random entrance of new job orders for one to 10 tasks; and, tasks’ priority values: eight to nine for high priority, four to seven for medium priority, and zero to three for low priority). The processing rules for this test are similar to those of the High Priority test, with the following difference: once the failure in the best machine is generated, a seeking process is started to find the minimum bid presented in the system (the least capable agent).

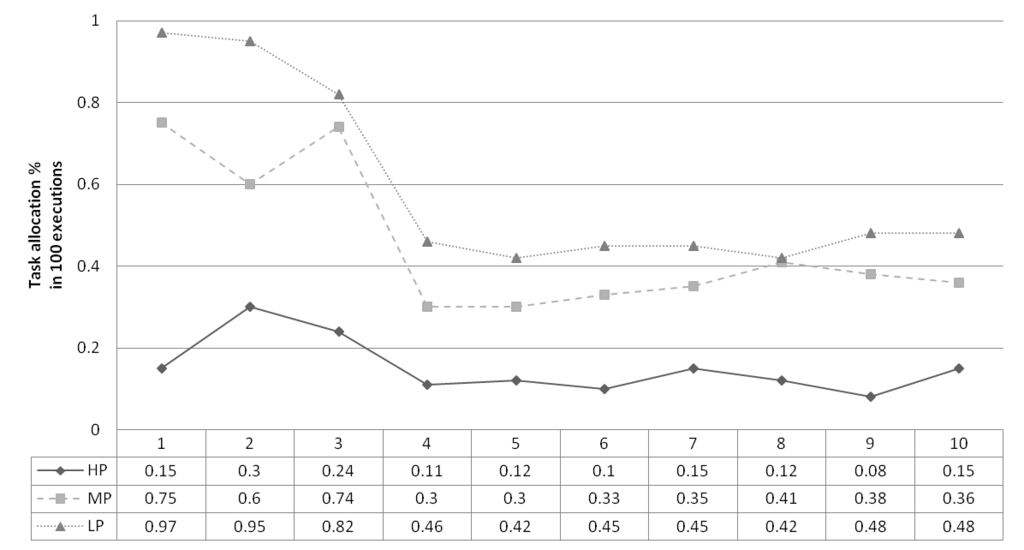
Figure 5 shows the percentage of allocated tasks when random job orders enter the system with different priority levels. Analyzing these results again reveals the difficulty to allocate high priority level tasks in the system when the task orders increases.

Figure 5. Rescheduling with High Utilization Test: Task allocation for zero to 10 task orders with high, medium, and low priority.

Figure 5. Rescheduling with High Utilization Test: Task allocation for zero to 10 task orders with high, medium, and low priority.

In the simulation using the High Utilization algorithm, the implemented Java code for the auctioneer seeks the lowest offer among the bidder agents and evaluates it against the randomly assigned value for the generated tasks. An independent routine is programmed in order to define a winner when the presented bids are equal; besides, three static functions use the bids as parameters to divide the information into decision blocks to allow the proper selection of the best bid for this particular case.

The allocation time using the High Utilization algorithm maintains practically the same observed levels in the application of the High Priority algorithm (arround 49 to 50 ms).

5.4. Priority Change Test

In this section the Priority Change test is decribed. In this test, the bidding-based MAS approach for task allocation is simulated with priority changes in the job orders that ramdonly enter the system. This way the average increment in the system saturation can be evaluated. For this test, the software simulator randomly generates the priority values as integer values in the range between zero and nine. To properly determine the coupled priority resulting from pairing two tasks of different values, the following conditions are considered: the total priority level is low if it falls in the range of zero to six, medium between seven and 12 and high between 13 and 18. For practical purposes, if the system is able to receive the job order at some initial priority but cannot complete it when its level is raised, it is considered oversaturated.

The high saturation in the system, when priority changes, is revealed in Figure 6 and in Table 5, with a 93% average for all the generated transitions, which leads to the conclusion that only with Low to Medium transitions the system has a good processing and allocating performance for the job tasks under this specific schema.

Figure 6. Average system saturation under simulations of the priority change test.

Figure 6. Average system saturation under simulations of the priority change test.

Table 5. Average system saturation levels.

Total Experiments	Low to Medium Priority	Medium to High Priority	Low to High Priority
1–20	83%	99%	99%
21–40	81%	96%	97%
41–50	92%	96%	98%

Table 5. Average system saturation levels.

Total Experiments	Low to Medium Priority	Medium to High Priority	Low to High Priority
1–20	83%	99%	99%
21–40	81%	96%	97%
41–50	92%	96%	98%

6. Performance Evaluation Analysis of the Algorithm

In this section, the overall performance of the bidding-based MAS approach when integrated by means of the algorithms presented in Section 5, to the diverse complexity scenarios is analyzed. The performance evaluation analysis considers the following: an optimum system performance is present when the processed orders are completed with a higher than initial priority (value), i.e., the best bidder agent is able to accelerate the process; good performance is presen if the best bidder is able to allocate the job order at the initial price, and finally, a bad performance is present when the order cannot be allocated (Figure 7).

Figure 7. Performance evaluation for different tests.

Figure 7. Performance evaluation for different tests.

Analyzing the results in Figure 7, it is clear that the overall behavior of the bidding-based MAS approach is good, on average, for those situations in which a high rescheduling requirement is present. For dynamic environments its behavior is not bad. Nevertheless, the number of unallocated tasks is higher than in the other tests.

In Figure 8, it can be noticed that the unallocated (NA) job level for the Dynamic environment Test is minimal (7%) and the entire allocation level is relatively high; however, a substantial amount of allocated jobs corresponds to low priority level orders, almost three times the result of high priority orders. Under the same optimum, good and bad classification scenarios, the High Priority test application results (Figure 8) show that despite the absence of the best bidder agent and the consequent utilization of an alternative, the accumulated amount of successfully allocated jobs is above 70%; however, categorizing the results, the high amount of unallocated jobs, almost equiparable to every allocated order category, is noticable.

For the High Utilization test, just as in the previous case, a failure occurrence in the best bidder agent is generated. Under these conditions, the alternative agent will be the least optimal. As expected, the amount of successfully completed orders decreases significantly (Figure 8). Furthermore, when the results for every priority level are distributed, the successfully completed high priority job order level is below 10%. Contrary to this, the low priority allocation level increases, reaching 32% on average.

Figure 8. Task allocation distribution for different test and different priority values.

Figure 8. Task allocation distribution for different test and different priority values.

The final perspective is the Priority Change test analysis shown in Figure 6. In this, the average saturation level of the entire system is measured, i.e., the system behavior when higher than initial priority levels are generated for all cases. For practical reasons, when reaching a 100% or higher saturation measure, the system is considered to surpass its capacity for processing incoming orders; for this reason, with the obtained values over 90% on average, it can be concluded that the system performs highly saturated under this conditions.

7. Robustness Measure Analysis of the Bidding-Based Algorithm

In this section, the robustness of the bidding-based MAS approach for task allocation is analyzed.

An optimized system, in a classical sense, can be very sensitive to small changes, without previous notification. It is preferable to design a system capable of delivering a high robustness level. Marczyk states that “optimization is precisely the opposite of robustness” [37] and, in this context, the system design is aimed at finding optimal solutions for the creation of a robust system. Precisely, the modeling process to attain this objective requires solving all related optimization problems, which are susceptible to demanding too much computing power [38].

The robustness of a schedule is not an easy concept to measure or even to define. A robustness measure can be calculated from the amount of lost time between the order finishing time and the order shipping time. In this case, a possible schedule robustness measure can be defined as:

$$R\left(S\right)=\frac{{{\displaystyle \sum }}_{j=1}^n{\text{ω}}_j\left(d_j-C_j\right)}{\Sigma {\text{ω}}_j{d}_j}$$

(1)

where:

$d_j$, is the shipping time for job order j.

$C_j$, is the makespan for j.

${\text{ω}}_j$, is a weigh (priority) value assigned to the job order j.

This way the robustness measure becomes better as the value of R(S) increases.

Consider, for example, the processing time, shipping time, and priority values shown in Table 6 for three jobs.

Table 6. Initial values for simulation.

Values	Job 1	Job 2	Job 3
pj	10	10	10
dj	10	22	34
ωj	1	100	100

Table 6. Initial values for simulation.

Values	Job 1	Job 2	Job 3
pj	10	10	10
dj	10	22	34
ωj	1	100	100

C_j, can be calculated from the cumulative processing time of the given job. In this case from Table 6 the following values are derived: C₁ = 10, C₂ = 20 and C₃ = 30.

The robustness measure using Equation (1) for schedule <1,2,3> is:

$$R\left(<1,2,3>\right)=\frac{600}{5610}=0.11$$

while for the sequence <2,3,1>, the robustness measure is higher:

$$R\left(<2,3,1>\right)=\frac{2580}{5610}=0.46$$

which means the second schedule is more robust than the first one. Moreover, this sequence has the higher value when analyzing all the possible sequences for this particular example.

In order to measure the robustness level of the generated schedules from the bidding-based MAS approach, a set of simulation tests taking into account the following issues, was executed:

−

Oe the process is initialized, if the task is allocated at first bid, the p_j value remains without changes; however, if the capacity of the bidder allows the allocation at a higher value, the processing time is reduced and the p_j value is decreased in one time unit; however, in the case that the job could not be allocated, a system delay is considered and two time units are added for the processing time p_j

−

Fty simulation tests were executed for this test, measuring the robustness index for each one and calculating their general average in order to obtain a comparative index against the optimal robustness level calculated initially.

As an example, when there is no adjudication of any task into the MAS, the robustness index level is defined as follows:

$$R\left(<2,3,1>\right)=\frac{100\times 6+100\times 8+1\times \left(-26\right)}{5610}=0.24$$

The general results from the robustness test reveals a 0.29 robustness unit for the average case (a 37% of the robustness measure for the most robust sequence) and a 0.38 robustness unit (17%) for the maximum capacity allocation in the system. Those values were calculated measuring the probability of interruption ocurrence, as well as the ability for reprogramming the assigned job tasks [39].

8. Conclusions

The research goal of the work presented in this paper is to provide a mechanism to measure the performance of agent-based scheduling approaches for manufacturing systems under key critical situations such as dynamic environment, rescheduling, and priority change. With this mechanism it will be possible to simulate critical situations and to stress the system in order to measure a given agent-based scheduling method performance. In this work a specific method developed for bidding-based or market-like multi-agent approaches for manufacturing scheduling was presented. The method presented and the evaluation test performed revealed that the bidding algorithm integrated into MAS is a useful model for effective utilization in real applications. However, some operating elements are in need of improvement, such as the system capacity for allocating job orders on failure occurrences into the best agents, which directly affects the robustness level. In addition, it is required that the methodology can include real measurement elements like operating times, incoming data with real variation, storing, and real time incorporation of historical data, among others.

In order to complete the mechanism for performance measure of agent-based scheduling approaches, more work is being developed in order to provide specific measurement methods for other kinds of agent-based scheduling approaches such as temperature equilibrium, swarm intelligence, etc. This will make it possible to have a performance measurement package that can be used to measure different agent-based approaches under different critical situations that affect the task allocation problem in manufacturing systems.