Figure 1.
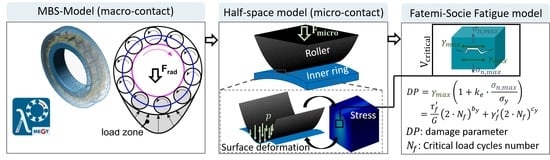
Schematic illustration of the entire modeling approach based on two contact models: MBS model in which the rolling element loads are determined from the entry into the load zone (at the angular position ) to the exit (at the angular position ), half-space model in which the stresses resulting in the inner ring (IR) (X: axial direction, Y: circumferential direction, Z: depth direction) are calculated and serve as input for the fatigue life estimation in the Fatemi-Socie model.
Figure 1.
Schematic illustration of the entire modeling approach based on two contact models: MBS model in which the rolling element loads are determined from the entry into the load zone (at the angular position ) to the exit (at the angular position ), half-space model in which the stresses resulting in the inner ring (IR) (X: axial direction, Y: circumferential direction, Z: depth direction) are calculated and serve as input for the fatigue life estimation in the Fatemi-Socie model.
Figure 2.
Illustration of the contact models used in both simulation levels, (a) macroscale MBS model and (b) microscale half-space model.
Figure 2.
Illustration of the contact models used in both simulation levels, (a) macroscale MBS model and (b) microscale half-space model.
Figure 3.
Maximum contact forces in the rolling bearing inner ring contact were determined using the MBS model.
Figure 3.
Maximum contact forces in the rolling bearing inner ring contact were determined using the MBS model.
Figure 4.
Comparison of the half-space elastic contact results with those of Hertz theory using the example of a line contact in a cylindrical roller bearing NU208 for the load case 2.4 GPa for an ideally smooth inner ring geometry.
Figure 4.
Comparison of the half-space elastic contact results with those of Hertz theory using the example of a line contact in a cylindrical roller bearing NU208 for the load case 2.4 GPa for an ideally smooth inner ring geometry.
Figure 5.
Schematic representation of the two basic concepts of material fatigue considered in the Fatemi–Socie model, (a) initiation of the slip bands (also places of microcrack initiation) by the shear stress τ, (b) microcrack expansion by the normal stress σ.
Figure 5.
Schematic representation of the two basic concepts of material fatigue considered in the Fatemi–Socie model, (a) initiation of the slip bands (also places of microcrack initiation) by the shear stress τ, (b) microcrack expansion by the normal stress σ.
Figure 6.
Left: stress component on a critical volume element for each angular position, middle: determination for each angular position of the normal and shear stresses on any plane Π of the critical volume element, right: result as input variables for the determination of the shear stress vectors.
Figure 6.
Left: stress component on a critical volume element for each angular position, middle: determination for each angular position of the normal and shear stresses on any plane Π of the critical volume element, right: result as input variables for the determination of the shear stress vectors.
Figure 7.
Plotting the angular position dependent shear stress vectors for a plane to determine the shear stress amplitude.
Figure 7.
Plotting the angular position dependent shear stress vectors for a plane to determine the shear stress amplitude.
Figure 8.
Schematic illustration of the bearing test rig.
Figure 8.
Schematic illustration of the bearing test rig.
Figure 9.
Surface analysis using a NANOFOCUS μSurf EXPLORER confocal microscope: Measurement setup (left) and CAD model (right).
Figure 9.
Surface analysis using a NANOFOCUS μSurf EXPLORER confocal microscope: Measurement setup (left) and CAD model (right).
Figure 10.
Measured real inner ring surface (a) rough ground, (b) hard turned, and (c) fine ground in manufactured and in run-in states.
Figure 10.
Measured real inner ring surface (a) rough ground, (b) hard turned, and (c) fine ground in manufactured and in run-in states.
Figure 11.
Elastically simulated contact pressures with of real surfaces (a): rough ground, (b) hard turned, and (c) fine ground bearing ring in manufactured (top) and run-in states (bottom).
Figure 11.
Elastically simulated contact pressures with of real surfaces (a): rough ground, (b) hard turned, and (c) fine ground bearing ring in manufactured (top) and run-in states (bottom).
Figure 12.
Elastically simulated vs. Mises stresses in contact of real surfaces; (a) rough ground, (b) hard ground, and (c) fine ground bearing ring in manufactured (top) and in run-in states (bottom).
Figure 12.
Elastically simulated vs. Mises stresses in contact of real surfaces; (a) rough ground, (b) hard ground, and (c) fine ground bearing ring in manufactured (top) and in run-in states (bottom).
Figure 13.
(a): Elasto-plastic simulated variation of the true contact area under cyclic indentation, (b): Simulation time for the respective load cycles.
Figure 13.
(a): Elasto-plastic simulated variation of the true contact area under cyclic indentation, (b): Simulation time for the respective load cycles.
Figure 14.
Elasto-plastically simulated contact pressure after 200 load cycles.
Figure 14.
Elasto-plastically simulated contact pressure after 200 load cycles.
Figure 15.
Evaluation of the simulated tangential residual stresses on the section plane through the volume element (a) a zoom window (b) and the maximum compressive residual stress in the section (c).
Figure 15.
Evaluation of the simulated tangential residual stresses on the section plane through the volume element (a) a zoom window (b) and the maximum compressive residual stress in the section (c).
Figure 16.
Experimental determination of the load-induced residual stress component in (c), by subtracting the measured residual stresses on the inner ring in the unloaded state (a) from the loaded state (b).
Figure 16.
Experimental determination of the load-induced residual stress component in (c), by subtracting the measured residual stresses on the inner ring in the unloaded state (a) from the loaded state (b).
Figure 17.
Computed stress components on the critical volume element (at depths of 125 μm and 1.17 μm for simulation cases with the ideally smooth and rough inner ring geometry, respectively) for different angular positions.
Figure 17.
Computed stress components on the critical volume element (at depths of 125 μm and 1.17 μm for simulation cases with the ideally smooth and rough inner ring geometry, respectively) for different angular positions.
Figure 18.
Maximum shear strain amplitude on all discretized planes 𝛱 of the critical volume element for the surface variants: ideally smooth, fine ground, hard turned and rough ground.
Figure 18.
Maximum shear strain amplitude on all discretized planes 𝛱 of the critical volume element for the surface variants: ideally smooth, fine ground, hard turned and rough ground.
Figure 19.
Illustration of the orientation of the critical plane in the simulations with ideally smooth and rough inner ring surfaces.
Figure 19.
Illustration of the orientation of the critical plane in the simulations with ideally smooth and rough inner ring surfaces.
Figure 20.
Profile of the normal stress perpendicular to the critical plane; maximum pressure normal stress marked with a asterisk.
Figure 20.
Profile of the normal stress perpendicular to the critical plane; maximum pressure normal stress marked with a asterisk.
Table 1.
Geometric and load variables of the MBS model and half-space model.
Table 1.
Geometric and load variables of the MBS model and half-space model.
| Macro-Variables | Micro-Variables |
|---|
| /mm | 10 | /mm | 0.6 |
| /mm | 49.98 | /mm | 0.6 |
| /mm | 9.7 | | |
| /N | 4986 | /N | 310 |
Table 2.
Microplastic material parameters of the Swift hardening model for 100Cr6 rolling bearing steel [
10,
14,
16,
17].
Table 2.
Microplastic material parameters of the Swift hardening model for 100Cr6 rolling bearing steel [
10,
14,
16,
17].
| Parameters | Value |
|---|
| /MPa | 945 |
| /- | 40 |
| /- | 0.121 |
Table 3.
Uniaxial cyclic material properties for the material group steel according to the FKM method [
4,
5] as a function of tensile strength.
Table 3.
Uniaxial cyclic material properties for the material group steel according to the FKM method [
4,
5] as a function of tensile strength.
| Parameters | Value |
|---|
| 3.1148 |
| −0.097 |
| |
| −0.52 |
| Validity range | MPa |
Table 4.
Material parameters using in the Fatemi–Socie fatigue life model.
Table 4.
Material parameters using in the Fatemi–Socie fatigue life model.
| Parameters | Value |
|---|
| /MPa | 1953 |
| /MPa | 1656 |
| /MPa | 80,769 |
| /− | 0.148 |
| /− | −0.097 |
| /− | −0.52 |
Table 5.
Relevant characteristics of the 3D confocal microscope.
Table 5.
Relevant characteristics of the 3D confocal microscope.
| Parameters | Unit | Value |
|---|
| Magnification | - | 20 |
| Measuring field | μm | 800 × 800 |
| Numerical aperture | - | 0.6 |
| Working distance | mm | 0.9 |
| Resolution in depth direction | nm | 4 |
| Resolution in the plane | μm | 1.6 |
Table 6.
Surface-related roughness parameters and in the manufactured state and in the run-in state, as mean value ± standard deviation of the repeat measurements.
Table 6.
Surface-related roughness parameters and in the manufactured state and in the run-in state, as mean value ± standard deviation of the repeat measurements.
| | Manufactured State | Run-In State (107. rev.) |
|---|
| | /μm | /μm | /μm | /μm |
| rough ground | 0.413 ± 0.001 | 0.392 ± 0.003 | 0.329 ± 0.001 | 0.310 ± 0.001 |
| hard turned | 0.168 ± 0.002 | 0.163 ± 0.004 | 0.113 ± 0.003 | 0.091 ± 0.000 |
| fine ground | 0.078 ± 0.001 | 0.061 ± 0.002 | 0.092 ± 0.002 | 0.083 ± 0.002 |
Table 7.
Simulated true contact areas of the measured rough surfaces in manufactured and run-in (after 107 revolutions) states.
Table 7.
Simulated true contact areas of the measured rough surfaces in manufactured and run-in (after 107 revolutions) states.
| | Manufactured State | Run-In State (107 rev.) |
|---|
| | / | / |
| rough ground | 0.0883 | 0.1088 |
| hard turned | 0.1265 | 0.2037 |
| fine ground | 0.1275 | 0.1896 |
Table 8.
Calculated potential plastic zone as the number of volume elements Nvol with a von Mises equivalent stress value greater than the yield stress, for the measured surfaces in manufactured and in run-in state (after 107 revolutions).
Table 8.
Calculated potential plastic zone as the number of volume elements Nvol with a von Mises equivalent stress value greater than the yield stress, for the measured surfaces in manufactured and in run-in state (after 107 revolutions).
| | Manufactured State | Run-In State (107. Rev.) |
|---|
| | Nvol | Vol / % | Nvol | Vol / % |
| rough ground | 434,817 | 8.95 | 433,501 | 8.92 |
| hard turned | 81,493 | 1.68 | 477 | 0.0098 |
| fine ground | 46,515 | 0.9581 | 491 | 0.0101 |
Table 9.
Comparison of the elasto-plastic computed stress components at the critical volume element at the 200th load cycle with those from the elastic computation with the elasto-plastic computed flattened surfaces after the 200th load cycle.
Table 9.
Comparison of the elasto-plastic computed stress components at the critical volume element at the 200th load cycle with those from the elastic computation with the elasto-plastic computed flattened surfaces after the 200th load cycle.
| | Rough Ground | Hard Turned | Fine Ground |
|---|
| | elastic | elastic-plastic | elastic | elastic-plastic | elastic | elastic-plastic |
| /MPa | −1310 | −1379 | −1339 | −1406 | −1312 | 1380 |
| /MPa | −2193 | −2319 | −2319 | −2255 | −2117 | −2054 |
| /MPa | −3466 | −3477 | −3477 | −3476 | −3331 | −3327 |
| /MPa | −27 | −27 | −3 | −3 | −23 | −22 |
| /MPa | −59 | −59 | 48 | 48 | −210 | −210 |
| /MPa | 8 | 8 | 34 | 34 | −112 | −112 |
Table 10.
Summary of simulation results: damage parameter
, the critical number of load cycles
, the number of inner ring revolutions
,
calculated according to the ISO standard [
1], and experimentally determined fatigue life values life values
.
Table 10.
Summary of simulation results: damage parameter
, the critical number of load cycles
, the number of inner ring revolutions
,
calculated according to the ISO standard [
1], and experimentally determined fatigue life values life values
.
| Surfaces | | | | | |
|---|
| ideally smooth | 0.0027 | 722 | 95 | - | - |
| fine ground | 0.0028 | 381 | 50 | 28.9 | 49.0 |
| hard turned | 0.0028 | 355 | 47 | 27.7 | 78.0 |
| rough ground | 0.0030 | 234 | 30 | 23.7 | 27.1 |