Novel Process Modeling of Magnetic-Field Assisted Finishing (MAF) with Rheological Properties
Abstract
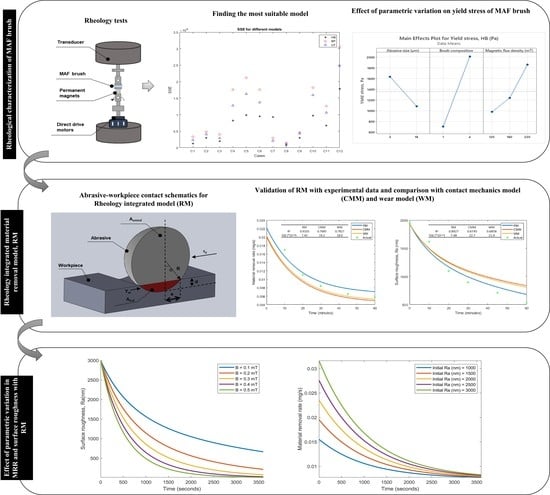
:1. Introduction
2. Materials and Methods
2.1. Rheology Tests
2.1.1. Design of Experiments
2.1.2. Rheology Models
2.1.3. Rheology Test Equipment, Tests and Rheological Parameters
2.2. Material Removal Model and Surface Roughness Model
2.2.1. Force and Number of Active Abrasives Calculation
2.2.2. Calculation of Indentation Depth
Contact Mechanics Model (CMM)
Wear Model (WM)
Proposed Rheology Integrated Model (RM)
2.2.3. Calculation of Material Removal Rate (MRR)
2.2.4. Calculation of Instantaneous Surface Roughness
3. Results and Discussion
3.1. Rheology Test Results
3.1.1. Selection of Best Rheological Model
3.1.2. Effect of Processing Conditions on Yield Stress
4. Material Removal Model Test Results
4.1. Calculation of MRR and Ra
4.2. Validation of MRR and Ra with Another Condition and Comparison of Various Models
4.3. Parametric Variation Results after Simulation
5. Conclusions
- Flow shear rate ramp data on the MAF brush showed a strong agreement with the HB model. The HB model was a better fit than the BP and CF models. GA was implemented to avoid the negative yield stress calculated by the HB model.
- Yield stress increased with magnetic flux density and iron-to-abrasive weight ratio and decreased with abrasive size. A larger abrasive size increased the inter-particle distance between iron particles and the interstitial spaces that a liquid carrier can occupy. These resulted in a lower magnetic force in the MAF brush and, subsequently, a lower yield stress.
- The new material removal model, rheology-integrated model (RM), formulated by integrating the yield stress of the MAF brush, predicted MRR and instantaneous roughness better than the pre-existing contact mechanics model and wear model.
- RM was used to predict MRR and surface roughness with different MAF conditions. Parametric variation results showed that the MRR increases with magnetic flux density, spindle speed, iron-to-abrasive weight ratio, and initial roughness, but decreases with abrasive size. The negative relation with abrasive size was due to the fact that the yield stress decreases with abrasive size, resulting in a loose brush and lower MRR.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shinmura, T.; Takazawa, K.; Hatano, E.; Matsunaga, M.; Matsuo, T. Study on magnetic abrasive finishing. CIRP Ann. Manuf. Technol. 1990, 39, 325–328. [Google Scholar] [CrossRef]
- Vahdati, M.; Rasouli, S.A. Study of magnetic abrasive finishing on freeform surface. Trans. IMF 2016, 94, 294–302. [Google Scholar] [CrossRef]
- Wang, L.; Sun, Y.; Chen, F.; Zhang, G.; Zhang, P.; Zuo, D. Experimental study on vibration-assisted magnetic abrasive finishing for internal blind cavity by bias external rotating magnetic pole. Precis. Eng. 2021, 74, 69–79. [Google Scholar] [CrossRef]
- Amnieh, S.K.; Mosaddegh, P.; Tehrani, A.F. Study on magnetic abrasive finishing of spiral grooves inside of aluminum cylinders. Int. J. Adv. Manuf. Technol. 2017, 91, 2885–2894. [Google Scholar] [CrossRef]
- Nguyen, H.X.; Suen, H.; Poudel, B.; Kwon, P.; Chung, H. Development of an innovative, high speed, large-scaled, and affordable metal additive manufacturing process. CIRP Ann. 2020, 69, 177–180. [Google Scholar] [CrossRef]
- Duda, T.; Raghavan, L.V. 3D Metal Printing Technology. IFAC-PapersOnLine 2016, 49, 103–110. [Google Scholar] [CrossRef]
- Slotwinski, J.A.; Garboczi, E.J. Metrology Needs for Metal Additive Manufacturing Powders. Jom 2015, 67, 538–543. [Google Scholar] [CrossRef]
- Poudel, B.; Nguyen, H.X.; O’neil, A.; Ahmad, M.U.; Qu, Z.; Kwon, P.; Chung, H. Selective Laser Melting and Mechanical Properties of Oxide Dispersion Strengthened Haynes 214 Alloy. In Volume 2: Manufacturing Processes; Manufacturing Systems; American Society of Mechanical Engineers: West Lafayette, IN, USA, 2022. [Google Scholar] [CrossRef]
- Nguyen, H.X.; Suen, H.; Poudel, B.; Qu, Z.; Ahmad, M.U.; Kwon, P.; Benard, A.; Chung, H. From Photopolymerization of Metal Suspension to Practical and Economical Additive Manufacturing of Haynes 214 Alloy for High Temperature Application. In Proceedings of the 2022 International Additive Manufacturing Conference, Lisbon, Portugal, 19–20 October 2022; American Society of Mechanical Engineers Digital Collection: Milpitas, CA, USA, 2022. [Google Scholar] [CrossRef]
- Mori, Y.; Yamauchi, K.; Endo, K. Elastic emission machining. Precis. Eng. 1987, 9, 123–128. [Google Scholar] [CrossRef]
- Ilie, F.; Minea, I.-L.; Cotici, C.D.; Hristache, A.-F. The Effects of Friction and Temperature in the Chemical–Mechanical Planarization Process. Materials 2023, 16, 2550. [Google Scholar] [CrossRef]
- Zhu, P.; Zhang, G.; Teng, X.; Du, J.; Jiang, L.; Chen, H.; Liu, N. Investigation and process optimization for magnetic abrasive finishing additive manufacturing samples with different forming angles. Int. J. Adv. Manuf. Technol. 2021, 118, 2355–2371. [Google Scholar] [CrossRef]
- Peng, X.; Kong, L.; Fuh, J.Y.H.; Wang, H. A Review of Post-Processing Technologies in Additive Manufacturing. J. Manuf. Mater. Process. 2021, 5, 38. [Google Scholar] [CrossRef]
- Wu, P.-Y.; Hirtler, M.; Bambach, M.; Yamaguchi, H. Effects of build- and scan-directions on magnetic field-assisted finishing of 316L stainless steel disks produced with selective laser melting. CIRP J. Manuf. Sci. Technol. 2020, 31, 583–594. [Google Scholar] [CrossRef]
- Poudel, B.; Lee, P.-H.; Song, G.; Nguyen, H.; Kim, K.; Jung, K.; Shao, C.; Kwon, P.; Chung, H. Innovative Magnetic-Field Assisted Finishing (MAF) Using Nano-Scale Solid Lubricant: A Case Study on Mold Steel. Int. J. Precis. Eng. Manuf. Technol. 2021, 9, 1411–1426. [Google Scholar] [CrossRef]
- Kim, J.; Kim, H.; Lee, S.H. Selective Magnetic Abrasive Finishing of Nano-Thickness IZO-Coated Pyrex Glass Using Acoustic Emission Monitoring and Artificial Neural Network. IEEE Access 2019, 7, 136783–136791. [Google Scholar] [CrossRef]
- Hou, Z.-B.; Komanduri, R. Magnetic Field Assisted Finishing of Ceramics—Part III: On the Thermal Aspects of Magnetic Abrasive Finishing (MAF) of Ceramic Rollers. J. Tribol. 1998, 120, 660–667. [Google Scholar] [CrossRef]
- Song, G.; Poudel, B.; Kwon, P.; Chung, H.; Detweiler, Z.; Quan, G. Development of Magnetic-Field Assisted Finishing (MAF) Process for Chromium-Alloyed Low Carbon Steel Sheet Metal. In Proceedings of the ASME 2021 16th International Manufacturing Science and Engineering Conference, Cincinnati, OH, USA, 21–25 June 2021; American Society of Mechanical Engineers Digital Collection: Milpitas, CA, USA, 2021. [Google Scholar] [CrossRef]
- Yamaguchi, H.; Srivastava, A.K.; Tan, M.; Hashimoto, F. Magnetic Abrasive Finishing of cutting tools for high-speed machining of titanium alloys. CIRP J. Manuf. Sci. Technol. 2014, 7, 299–304. [Google Scholar] [CrossRef]
- Poudel, B.; Nguyen, H.X.; Kwon, P.; Chung, H. Selective laser melting of oxide dispersion strengthened MA956 alloy and its surface finishing by magnetic field assisted finishing. J. Manuf. Process. 2023, 97, 220–234. [Google Scholar] [CrossRef]
- Ahmad, S.; Gangwar, S.; Yadav, P.C.; Singh, D.K. Optimization of process parameters affecting surface roughness in magnetic abrasive finishing process. Mater. Manuf. Process. 2017, 32, 1723–1729. [Google Scholar] [CrossRef]
- Yang, L.-D.; Lin, C.-T.; Chow, H.-M. Optimization in MAF operations using Taguchi parameter design for AISI304 stainless steel. Int. J. Adv. Manuf. Technol. 2008, 42, 595–605. [Google Scholar] [CrossRef]
- Anjaneyulu, K.; Venkatesh, G. Optimization of process parameters of magnetic abrasive finishing using Jaya algorithm. Mater. Today Proc. 2020, 41, 1035–1040. [Google Scholar] [CrossRef]
- Singh, D.K.; Jain, V.; Raghuram, V.; Komanduri, R. Analysis of surface texture generated by a flexible magnetic abrasive brush. Wear 2005, 259, 1254–1261. [Google Scholar] [CrossRef]
- Shukla, V.C.; Pandey, P.M.; Dixit, U.S.; Roy, A.; Silberschmidt, V. Modeling of normal force and finishing torque considering shearing and ploughing effects in ultrasonic assisted magnetic abrasive finishing process with sintered magnetic abrasive powder. Wear 2017, 390–391, 11–22. [Google Scholar] [CrossRef]
- Gao, Y.; Zhao, Y.; Zhang, G.; Yin, F.; Zhang, H. Modeling of material removal in magnetic abrasive finishing process with spherical magnetic abrasive powder. Int. J. Mech. Sci. 2020, 177, 105601. [Google Scholar] [CrossRef]
- Misra, A.; Pandey, P.M.; Dixit, U. Modeling of material removal in ultrasonic assisted magnetic abrasive finishing process. Int. J. Mech. Sci. 2017, 131–132, 853–867. [Google Scholar] [CrossRef]
- Misra, A.; Pandey, P.M.; Dixit, U. Modeling and simulation of surface roughness in ultrasonic assisted magnetic abrasive finishing process. Int. J. Mech. Sci. 2017, 133, 344–356. [Google Scholar] [CrossRef]
- El-Taweel, T.A. Modelling and analysis of hybrid electrochemical turning-magnetic abrasive finishing of 6061 Al/Al2O3 composite. Int. J. Adv. Manuf. Technol. 2008, 37, 705–714. [Google Scholar] [CrossRef]
- Pashmforoush, F.; Rahimi, A.; Kazemi, M. Mathematical modeling of surface roughness in magnetic abrasive finishing of BK7 optical glass. Appl. Opt. 2015, 54, 8275–8281. [Google Scholar] [CrossRef] [PubMed]
- Shanbhag, V.V.; Naveen, K.; Balashanmugam, N.; Vinod, P. Modelling for evaluation of surface roughness in magnetic abrasive finishing of flat surfaces. Int. J. Precis. Technol. 2016, 6, 159. Available online: https://www.inderscienceonline.com/doi/abs/10.1504/IJPTECH.2016.078190 (accessed on 17 September 2021). [CrossRef]
- Kim, J.-D.; Choi, M.-S. Simulation for the prediction of surface-accuracy in magnetic abrasive machining. J. Mater. Process. Technol. 1995, 53, 630–642. [Google Scholar] [CrossRef]
- Kremen, G.Z.; Elsayed, E.A.; Rafalovich, V.I. Mechanism of material removal in the magnetic abrasive process and the accuracy of machining. Int. J. Prod. Res. 1996, 34, 2629–2638. [Google Scholar] [CrossRef]
- Rabinowicz, E.; Dunn, L.; Russell, P. A study of abrasive wear under three-body conditions. Wear 1961, 4, 345–355. [Google Scholar] [CrossRef]
- Jayswal, S.; Jain, V.; Dixit, P. Modeling and simulation of magnetic abrasive finishing process. Int. J. Adv. Manuf. Technol. 2005, 26, 477–490. [Google Scholar] [CrossRef]
- Li, W.; Li, X.; Yang, S.; Li, W. A newly developed media for magnetic abrasive finishing process: Material removal behavior and finishing performance. J. Mater. Process. Technol. 2018, 260, 20–29. [Google Scholar] [CrossRef]
- Jain, V. Magnetic field assisted abrasive based micro-/nano-finishing. J. Mater. Process. Technol. 2009, 209, 6022–6038. [Google Scholar] [CrossRef]
- Qian, C.; Fan, Z.; Tian, Y.; Liu, Y.; Han, J.; Wang, J. A review on magnetic abrasive finishing. Int. J. Adv. Manuf. Technol. 2021, 112, 619–634. [Google Scholar] [CrossRef]
- Preston, F.W. The Theory and Design of Plate Glass Polishing Machines. J. Glass Technol. 1927, 11, 214–256. Available online: https://cir.nii.ac.jp/crid/1571417125832111360 (accessed on 16 May 2022).
- Zhang, J.; Wang, H.; Kumar, A.S.; Jin, M. Experimental and theoretical study of internal finishing by a novel magnetically driven polishing tool. Int. J. Mach. Tools Manuf. 2020, 153, 103552. [Google Scholar] [CrossRef]
- Jain, V.K.; Jayswal, S.C.; Dixit, P.M. Modeling and Simulation of Surface Roughness in Magnetic Abrasive Finishing Using Non-Uniform Surface Profiles. Mater. Manuf. Process. 2007, 22, 256–270. [Google Scholar] [CrossRef]
- Ilie, F. Rheological behavior of the lubricants favoring the formation of thin layers by selective transfer in the frictional couples. Proc. Inst. Mech. Eng. Part J: J. Eng. Tribol. 2019, 233, 949–955. [Google Scholar] [CrossRef]
- Sidpara, A.; Jain, V.K. Rheological Properties and Their Correlation with Surface Finish Quality in MR Fluid-Based Finishing Process. Mach. Sci. Technol. 2014, 18, 367–385. [Google Scholar] [CrossRef]
- Sidpara, A.; Das, M.; Jain, V.K. Rheological Characterization of Magnetorheological Finishing Fluid. Mater. Manuf. Process. 2009, 24, 1467–1478. [Google Scholar] [CrossRef]
- Sapiński, B.; Horak, W. Rheological Properties of mr Fluids Recommended for Use in Shock Absorbers. Acta Mech. Autom. 2013, 7, 107–110. Available online: http://yadda.icm.edu.pl/baztech/element/bwmeta1.element.baztech-38a596e8-9cf7-4f25-80e7-9b8305e43c6b (accessed on 17 September 2021). [CrossRef]
- Huilgol, R.; You, Z. Application of the augmented Lagrangian method to steady pipe flows of Bingham, Casson and Herschel–Bulkley fluids. J. Non-Newtonian Fluid Mech. 2005, 128, 126–143. [Google Scholar] [CrossRef]
- Jain, V.; Kumar, R.; Dixit, P.; Sidpara, A. Investigations into abrasive flow finishing of complex workpieces using FEM. Wear 2009, 267, 71–80. [Google Scholar] [CrossRef]
- Pashmforoush, F.; Rahimi, A. Numerical-experimental study on the mechanisms of material removal during magnetic abrasive finishing of brittle materials using extended finite element method. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 230, 1498–1510. [Google Scholar] [CrossRef]
- Yi-Ling, W.; Zi-Shan, W. An analysis of the influence of plastic indentation on three-body abrasive wear of metals. Wear 1988, 122, 123–133. [Google Scholar] [CrossRef]
- Lin, Z.; Gao, B.; Li, X.; Yu, K. Effect of abrasive grain size on surface particle deposition behaviour of PTFE/bronze composites during abrasive wear. Tribol. Int. 2019, 139, 12–21. [Google Scholar] [CrossRef]
- Yang, S.; Li, W. Surface Quality and Finishing Technology. In Surface Finishing Theory and New Technology; Yang, S., Li, W., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; pp. 1–64. [Google Scholar] [CrossRef]
- De Larrard, F.; Ferraris, C.F.; Sedran, T. Fresh concrete: A Herschel-Bulkley material. Mater. Struct. 1998, 31, 494–498. [Google Scholar] [CrossRef]
- Chauhan, G.; Verma, A.; Das, A.; Ojha, K. Rheological studies and optimization of Herschel-Bulkley flow parameters of viscous karaya polymer suspensions using GA and PSO algorithms. Rheol. Acta 2018, 57, 267–285. [Google Scholar] [CrossRef]
- Kelessidis, V.; Maglione, R.; Tsamantaki, C.; Aspirtakis, Y. Optimal determination of rheological parameters for Herschel–Bulkley drilling fluids and impact on pressure drop, velocity profiles and penetration rates during drilling. J. Pet. Sci. Eng. 2006, 53, 203–224. [Google Scholar] [CrossRef]
- Rooki, R.; Ardejani, F.D.; Moradzadeh, A.; Mirzaei, H.; Kelessidis, V.; Maglione, R.; Norouzi, M. Optimal determination of rheological parameters for herschel-bulkley drilling fluids using genetic algorithms (GAs). Korea-Australia Rheol. J. 2012, 24, 163–170. [Google Scholar] [CrossRef]
- Chaudhuri, A.; Wereley, N.M.; Kotha, S.; Radhakrishnan, R.; Sudarshan, T.S. Viscometric characterization of cobalt nanoparticle-based magnetorheological fluids using genetic algorithms. J. Magn. Magn. Mater. 2005, 293, 206–214. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, J.Q.; Liu, J.N. Effect of Magnetic Field on Properties of Mr Fluids. Int. J. Mod. Phys. B 2005, 19, 597–601. [Google Scholar] [CrossRef]
- Nagdeve, L.; Sidpara, A.; Jain, V.K.; Ramkumar, J. On the effect of relative size of magnetic particles and abrasive particles in MR fluid-based finishing process. Mach. Sci. Technol. 2018, 22, 493–506. [Google Scholar] [CrossRef]
- Singh, D.K.; Jain, V.; Raghuram, V. Parametric study of magnetic abrasive finishing process. J. Mater. Process. Technol. 2004, 149, 22–29. [Google Scholar] [CrossRef]
- Bastaninejad, M.; Ahmadi, G. Modeling the Effects of Abrasive Size Distribution, Adhesion, and Surface Plastic Deformation on Chemical-Mechanical Polishing. J. Electrochem. Soc. 2005, 152, G720–G730. [Google Scholar] [CrossRef]

















| S.N. | Abrasive Size, D (µm) | Iron-to-Abrasive Weight Ratio | Magnetic Flux Density, B (mT) |
|---|---|---|---|
| C1 | 3 | 1:1 | 120 |
| C2 | 3 | 1:1 | 180 |
| C3 | 3 | 1:1 | 220 |
| C4 | 3 | 4:1 | 120 |
| C5 | 3 | 4:1 | 180 |
| C6 | 3 | 4:1 | 220 |
| C7 | 18 | 1:1 | 120 |
| C8 | 18 | 1:1 | 180 |
| C9 | 18 | 1:1 | 220 |
| C10 | 18 | 4:1 | 120 |
| C11 | 18 | 4:1 | 180 |
| C12 | 18 | 4:1 | 220 |
| Model | Constitutive Equations | |
|---|---|---|
| Bingham Plastic model | (1) | |
| Herschel–Bulkley model | (2) | |
| Casson fluid model | (3) | |
| Method | SSE | R2 | |||
|---|---|---|---|---|---|
| NL | −2764 | 4307 | 0.1247 | 2.02 × 107 | 0.861 |
| NLP | 0.00000154 | 1439 | 0.3011 | 2.324 × 107 | 0.8405 |
| GA | 1023.3 | 802.81 | 0.3599 | 2.08 × 107 | 0.7612 |
| Constituents | Weight Ratio (Miron: Mabrasive) −1 to 1 | Weight Ratio (Miron: Mabrasive) −4 to 1 | ||
|---|---|---|---|---|
| Mass (g) | Volume, mm3 (Volume %) | Mass (g) | Volume, mm3 (Volume %) | |
| Iron | 0.4902 | 51.9 (~10.57%) | 1.2422 | 157.77 (~32.14%) |
| Abrasive | 0.4902 | 132 (~26.89%) | 0.31056 | 100.177 (~20.37%) |
| Silicone oil | 0.6138 | 306.9 (~62.5%) | 0.4658 | 232.91 (~47.4%) |
| Time (min) | TMR (mg) | MRR (mg/s) | Roughness, Ra (µm) |
|---|---|---|---|
| 0 | 0 | 0 | 1.5782 |
| 10 | 6.3000 | 0.0105 | 1.2510 |
| 20 | 10.6000 | 0.0072 | 1.1580 |
| 30 | 13.7000 | 0.0052 | 1.0192 |
| 45 | 17.1000 | 0.0038 | 0.9460 |
| 60 | 19.4000 | 0.0026 | 0.9005 |
| 75 | 21.7000 | 0.0026 | 0.8858 |
| Experimental Conditions | |
|---|---|
| RPM | 2000 |
| Brush diameter | 18 mm |
| Clearance | 1 mm |
| Magnetic flux density | 120 or 180 or 220 mT |
| Abrasive diameter | 3 or 18 µm |
| Length of the workpiece | 30 mm |
| Brinell Hardness of Cena V steel | 375 |
| Ductility factor for steel, K | 3 [27] |
| Density of black ceramic abrasives | 3210 kg/m3 |
| Density of iron particles | 7874 kg/m3 |
| Density of workpiece | 7850 kg/m3 |
| Young’s modulus of workpiece | 208 GPa |
| Poisson’s ratio of workpiece | 0.303 |
| Young’s modulus of black ceramic abrasives | 410 GPa |
| Poisson’s ratio of black ceramic abrasives | 0.14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poudel, B.; Nguyen, H.; Song, G.; Kwon, P.; Chung, H. Novel Process Modeling of Magnetic-Field Assisted Finishing (MAF) with Rheological Properties. Lubricants 2023, 11, 239. https://doi.org/10.3390/lubricants11060239
Poudel B, Nguyen H, Song G, Kwon P, Chung H. Novel Process Modeling of Magnetic-Field Assisted Finishing (MAF) with Rheological Properties. Lubricants. 2023; 11(6):239. https://doi.org/10.3390/lubricants11060239
Chicago/Turabian StylePoudel, Bibek, Hoa Nguyen, Guangchao Song, Patrick Kwon, and Haseung Chung. 2023. "Novel Process Modeling of Magnetic-Field Assisted Finishing (MAF) with Rheological Properties" Lubricants 11, no. 6: 239. https://doi.org/10.3390/lubricants11060239
APA StylePoudel, B., Nguyen, H., Song, G., Kwon, P., & Chung, H. (2023). Novel Process Modeling of Magnetic-Field Assisted Finishing (MAF) with Rheological Properties. Lubricants, 11(6), 239. https://doi.org/10.3390/lubricants11060239