Effects of Hyperelliptic Bearings Bush on Connecting Rod Big-End Lubrication and Design Optimization
Abstract
:1. Introduction
2. Development of a Flexible Multi-Body Dynamics Model of the Connecting Rod
3. Bush Profile Design and Equation
4. Influence of Bush Profiles on the Lubrication Performance of Connecting Rod Big-End Bearing
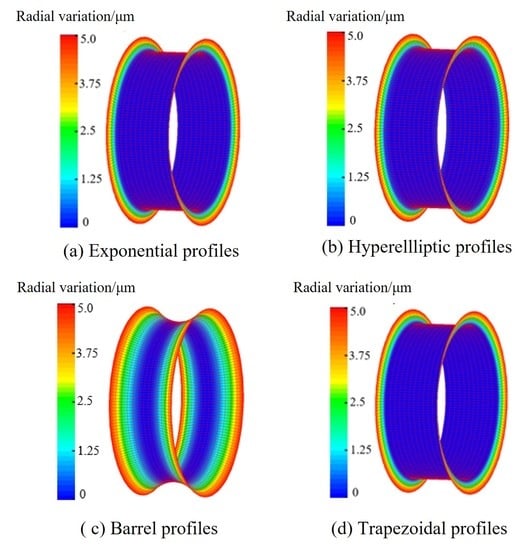
4.1. Exponential Bush Profiles
4.2. Hyperelliptic Bush Profiles
4.3. Barrel Bush Profiles
4.4. Trapezoidal Bush Profiles
5. Parameter Optimization of the Connecting Rod Big-End Bearing Based on the RBF Neural Network Model
5.1. Factor Selection and Design of Experiments
5.2. Emulator Model Building and Evaluation
5.3. Parameter Optimization of the Connecting Rod Big-End Bearing
6. Conclusions
- (1)
- When the maximum radial variation increased from the baseline profile, the MOFT first increased and then decreased, and the surface roughness contact pressure first decreased and then increased. The exponential, hyperelliptic, and trapezoidal profiles improved the comprehensive lubrication performance of the connecting rod. Denoting the maximum radial variation as 0.005 mm and 0.010 mm, the 0.005 mm profiles performed better than the 0.010 mm profiles;
- (2)
- By using the best profile type, the hyperelliptic profile, a DoE simulation was conducted with four factors, i.e., bearing clearance, bearing width, journal oil hole diameter, and oil supply pressure. The RBF neural network model was developed to fit the DoE data. The MOFT and the APASP were used as two objective functions in optimization. The NSGA-II method was used to complete multi-objective optimization. The optimized MOFT increased from 1.56 μm to 1.97 μm, and the optimized APASP decreased from 3.97 MPa to 0.25 MPa.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, Z.; Wang, G.; Wang, Y.; Zhang, L.; Xu, C.; Wu, Y.; Li, X. Comparison of lubrication and structure for connecting rod small end bearing for an 8v diesel engine. Veh. Engine 2017, 2, 78–82. [Google Scholar]
- Zhang, Z.; Liu, J.; Song, X.; Zhang, L.; Zhao, Z.; Liu, Y.; Liang, Y. Lubrication characteristics analysis of connecting rod small end bearing and piston pin for diesel engine. Veh. Engine 2018, 3, 59–66. [Google Scholar]
- Moiseev, Y. Analysis and validation of the dynamic method for diagnosing diesel engine connecting rod bearings. Transp. Probl. 2018, 13, 123–133. [Google Scholar]
- Huang, F.; Peng, J.; Bi, Y.; Li, N.; Lei, J. A study of bearing thermal elastohydrodynamic lubrication characteristics for non-road diesel engine. Lubr. Eng. 2019, 44, 57–64+70. [Google Scholar]
- Qin, Z.; Xiang, J.; Zhong, C.; Li, C. The influence of connecting rod small end bushing profile on its friction pair lubrication and deformation characteristics. Chin. Intern. Combust. Engine Eng. 2020, 41, 70–79. [Google Scholar]
- He, Z.; Sun, Y.; Zhang, G.; Hong, Z.; Xie, W.; Lu, X.; Zhang, J. Tribilogical performances of connecting rod and by using orthogonal experiment, regression method and response surface methodology. Appl. Soft Comput. J. 2015, 29, 436–449. [Google Scholar] [CrossRef]
- Lavie, T.; Fransisco, A.; Fatu, A.; Villechaise, B. Multiobjective optimization of conrod big-end bearing lubrication using an evolutionary algorithm. Tribol. Trans. 2015, 58, 490–499. [Google Scholar] [CrossRef]
- Bi, F.; Liu, B.; Liu, C.; Tian, C.; Li, X.; Ma, T. Research on the lubrication of diesel engine connecting rod small end bearing based on thermoelastic model. Intern. Combust. Engine Eng. 2018, 39, 15–22. [Google Scholar]
- Wu, Q.; Zhou, R.; Chen, T.; Dong, C.; Zhang, G. Lubrication analysis of connecting rod bearings of two stroke marine diesel engine based on multi-body dynamics. Lubr. Eng. 2019, 44, 103–108. [Google Scholar]
- Ruan, D.; Chen, L.; Gao, Z. Effects of shell profile modification of engine conrod bearings on lubrication characteristics. China Mech. Eng. 2019, 30, 1207–1211+1218. [Google Scholar]
- Zhang, J. Study on Lubrication Performance of U-Shaped Connecting Rod Large Head Bearing. Master’s Thesis, Shandong University, Ji’nan, China, 2016. [Google Scholar]
- Bernhauser, L.; Heinisch, M.; Schörgenhumer, M.; Nader, M. The Effect of Non-Circular Bearing Shapes in Hydrodynamic Journal Bearings on the Vibration Behavior of Turbocharger Structures. Lubricants 2017, 5, 6. [Google Scholar] [CrossRef] [Green Version]
- Offner, G.; Knaus, O. A Generic Friction Model for Radial Slider Bearing Simulation Considering Elastic and Plastic Deformation. Lubricants 2015, 3, 522. [Google Scholar] [CrossRef] [Green Version]
- Razavykia, A.; Delprete, C.; Baldissera, P. Numerical Study of Power Loss and Lubrication of Connecting Rod Big-End. Lubricants 2019, 7, 47. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C. Study on the Effect of Connecting Rod Recirculation on the Elastic Hydrodynamic Lubrication Characteristics of Connecting Rod Bearings. Master’s Thesis, Kunming University of Science and Technology, Kunming, China, 2016. [Google Scholar]
- Zhang, L.; Wang, G.; Wang, Y.; Zhao, Z.; Zhang, Z.; Song, X. Wear analysis and surface profile design of a diesel engine piston pin bearing. Acta Armamentarii 2018, 39, 1892–1900. [Google Scholar]
- Chen, K. Experimental Design and Analysis; Tsinghua University Press: Beijing, China, 2005. [Google Scholar]
- Lai, Y. Isight Parameter Optimization Theory and Examples in Detail; Beijing University of Aeronautics and Astronautics Press: Beijing, China, 2012. [Google Scholar]
- Yuan, K.; Liu, Y.; Sun, J.; Luo, X. Research on control of underwater manipulator based on fuzzy RBF neural network. Chin. J. Eng. Des. 2019, 26, 675–682. [Google Scholar]
- Wang, D.; Wang, L.; Chen, Z.; Wu, X.; Zhang, S. Application of robustness and light weight in optimal design of door structure. Mech. Sci. Technol. Aerosp. Eng. 2019, 38, 626–633. [Google Scholar]














| Parameter (Unit) | Value |
|---|---|
| Number of cylinders | 2 |
| Firing order | 1–2 |
| Bore × stroke (mm) | 92 × 97 |
| Connecting rod length (mm) | 166 |
| Crank-to-rod ratio | 0.29 |
| Cylinder centerline distance (mm) | 124 |
| Engine speed (r/min) | 3200 |
| Rated power (kW) | 45 |
| Parameter (Unit) | Value |
|---|---|
| Bearing width (mm) | 25 |
| Bearing hole diameter (mm) | 56 |
| Bearing radial clearance (mm) | 0.03 |
| Lubricant oil type | 5 W–30 |
| Lubricant oil supply pressure (bar) | 4 |
| Cavitation pressure (bar) | 0.98 |
| Ambient pressure (bar) | 1 |
| Journal surface roughness height (μm) | 0.4 |
| Bearing surface roughness height (μm) | 0.8 |
| Profile Type | Minimum Oil Film Thickness (μm) | Roughness Contact Pressure (MPa) |
|---|---|---|
| Traditional straight bush profile | 1.11 | 71.57 |
| Exponential | 1.54 | 19.54 |
| Hyperelliptic | 1.56 | 18.32 |
| Barrel | 1.39 | 32.28 |
| Trapezoidal | 1.51 | 21.49 |
| Factor Level | A: Bearing Clearance (μm) | B: Bearing Width (mm) | C: Journal Oil Hole Diameter (mm) | D: Oil Supply Pressure (bar) |
|---|---|---|---|---|
| 1 | 26 | 22.4 | 5 | 4 |
| 2 | 56 | 28 | 6 | 5 |
| 3 | 86 | 33.6 | 7 | 6 |
| Run | A | B | C | D | MOFT (μm) | APASP (MPa) |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 2 | 2 | 0.797 | 4.88 |
| 2 | 1 | 3 | 2 | 2 | 1.645 | 0.98 |
| 3 | 3 | 1 | 2 | 2 | 0.748 | 7.02 |
| 4 | 3 | 3 | 2 | 2 | 1.474 | 1.55 |
| 5 | 2 | 2 | 1 | 1 | 1.890 | 0.28 |
| 6 | 2 | 2 | 1 | 3 | 1.892 | 0.27 |
| 7 | 2 | 2 | 3 | 1 | 1.891 | 0.27 |
| 8 | 2 | 2 | 3 | 3 | 1.891 | 0.27 |
| 9 | 1 | 2 | 2 | 1 | 1.799 | 0.49 |
| 10 | 1 | 2 | 2 | 3 | 1.853 | 0.43 |
| 11 | 3 | 2 | 2 | 1 | 1.781 | 0.49 |
| 12 | 3 | 2 | 2 | 3 | 1.778 | 0.49 |
| 13 | 2 | 1 | 1 | 2 | 0.797 | 5.15 |
| 14 | 2 | 1 | 3 | 2 | 0.780 | 5.11 |
| 15 | 2 | 3 | 1 | 2 | 1.598 | 0.99 |
| 16 | 2 | 3 | 3 | 2 | 1.612 | 0.97 |
| 17 | 1 | 2 | 1 | 2 | 1.805 | 0.48 |
| 18 | 1 | 2 | 3 | 2 | 1.813 | 0.48 |
| 19 | 3 | 2 | 1 | 2 | 1.781 | 0.49 |
| 20 | 3 | 2 | 3 | 2 | 1.778 | 0.49 |
| 21 | 2 | 1 | 2 | 1 | 0.797 | 5.16 |
| 22 | 2 | 1 | 2 | 3 | 0.800 | 5.10 |
| 23 | 2 | 3 | 2 | 1 | 1.598 | 0.99 |
| 24 | 2 | 3 | 2 | 3 | 1.617 | 0.95 |
| 25 | 2 | 2 | 2 | 2 | 1.892 | 0.27 |
| Factors and Responses | Value | Relative Change | |
|---|---|---|---|
| Initial | Optimum | ||
| A | 28 μm | 28.35 μm | 1.3% |
| B | 25 mm | 29.25 mm | 17.0% |
| C | 6 mm | 6.24 mm | 4.0% |
| D MOFT | 4 bar 1.56 μm | 5.99 bar 1.93 μm | 49.8% 23.7% |
| APASP | 3.97 kPa | 0.24 kPa | 93.9% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, D.; Li, C.; Deng, W.; Ji, H.; Hao, L. Effects of Hyperelliptic Bearings Bush on Connecting Rod Big-End Lubrication and Design Optimization. Lubricants 2023, 11, 293. https://doi.org/10.3390/lubricants11070293
Jia D, Li C, Deng W, Ji H, Hao L. Effects of Hyperelliptic Bearings Bush on Connecting Rod Big-End Lubrication and Design Optimization. Lubricants. 2023; 11(7):293. https://doi.org/10.3390/lubricants11070293
Chicago/Turabian StyleJia, Dewen, Chengkun Li, Wei Deng, Huiping Ji, and Lina Hao. 2023. "Effects of Hyperelliptic Bearings Bush on Connecting Rod Big-End Lubrication and Design Optimization" Lubricants 11, no. 7: 293. https://doi.org/10.3390/lubricants11070293
APA StyleJia, D., Li, C., Deng, W., Ji, H., & Hao, L. (2023). Effects of Hyperelliptic Bearings Bush on Connecting Rod Big-End Lubrication and Design Optimization. Lubricants, 11(7), 293. https://doi.org/10.3390/lubricants11070293