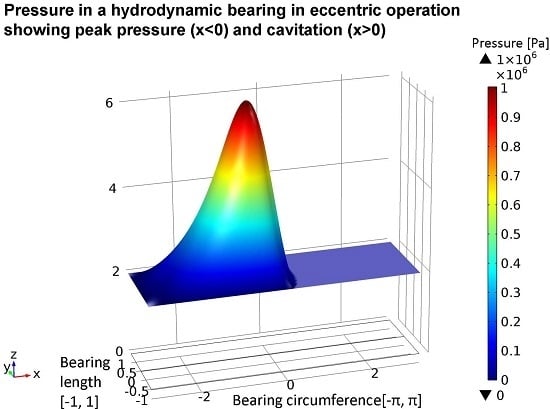
The distribution of pressure
p and mass fraction
f in a 2D lubricating film with film thickness
h can be described using the Reynolds equation:
where
and
U are the viscosity, density and surface velocity, respectively.
x- and
y-directions are in the direction of and perpendicular to the surface sliding velocity, respectively. It is assumed that only the shaft has velocity
U in the
x-direction; all other surfaces are stationary. Moreover, all surfaces are assumed to be rigid. As schematically depicted in
Figure 1a, the attitude angle
can be calculated as follows:
where
ε is the eccentricity ratio
.
and
are the global coordinates with the origin in the center of the bearing. Assuming perfect alignment of the journal and taking into account the attitude angle
, the expression for the film thickness may be written as:
where
is the nominal radial clearance. For the sake of numerical robustness, the problem is scaled using the following dimensionless variables:
which results in the following dimensionless Reynolds equation:
where the normalized film thickness is given by:
Note that the circumferential and axial flows,
and
, respectively, are represented by the terms between brackets
in Equation
5 and can thus simply be computed as follows:
This logic has been captured by the proposed cavitation algorithm, based on a variable transformation where both the mass fraction
f and the pressure
p are replaced by known functions of a new variable
ξ:
where
and
are Boolean expressions, equal to one if true and zero if not true. This transformation resembles Elrod’s algorithm [
7], although the algorithm proposed here has some different properties. Firstly, the Boolean functions are present both in the pressure and in the mass fraction functions, instead of just in the pressure function. Furthermore, the pressure and mass fraction functions are independent of each other. Thus, both functions can be optimally scaled for a stable numerical solution, which is an advantage compared to Elrod’s transformation,
i.e., the transformation constant
can be equal to any desired positive value. For Elrod’s transformation to be numerically stable, the bulk modulus has to be 10- to 100-times smaller than the value considered by Elrod, which at least reduces the physical meaning of the transformation [
15,
16]. Moreover, the accuracy of Elrod’s transformation is not always optimal, as it will result in mass fractions slightly above one in full film regions.
2.1. 1D Stationary Situation: Streamline Numerical Stabilization
The characteristics of the proposed transformation will first be tested on a simple 1D problem: the statically-loaded, infinitely long plain journal bearing. In the remainder of this section, it is assumed that the supply groove is infinitely small in the circumferential direction. Furthermore, we assume incompressible
lubricant properties. Considering this simplification and substituting Equation (8a) and (8b) in Equation (
5), the following 1D Reynolds equation is obtained:
In the 1D-domain, the dimensionless pressure is set equal to one at the supply (
) (BC1:
). It is worth mentioning that in this analysis, it is assumed that the derivative of the Boolean expression is zero and not equal to the Dirac-delta function. It is difficult to solve Equation (
9) using the standard Galerkin finite element approach because in the cavitated region
, the equation is purely convection dominated and, thus, will exhibit oscillations when solved using a standard Galerkin FEM. This can be observed in
Figure 2a, where the dependent variable
ξ and the dimensionless flow
have been plotted against the dimensionless length. Plotting
ξ provides direct insight into both the pressure and mass fraction distribution.
In the literature [
17,
18,
19], one may find many approaches to numerically stabilize the FEM solution of the convection-dominated part in convection-diffusion equations. Some of these methods are the streamline upwind Petrov-Galerkin method (SUPG), the SU method and the artificial diffusion method (AD). The SUPG method adds an additional term to the test function to suppress the unwanted oscillations, whereas the SU method only adds the additional term to the convection-dominated part of the equation [
19]. In the AD method, the diffusion part, of the convection-diffusion equation, is slightly modified with an additional artificial diffusion term in the convection-dominated part of the film.
Other techniques in the literature that deal with the convection-dominated aspect include semi-Lagrangian (or characteristic) methods [
20,
21]. The semi-Lagrangian technique has the advantage that it does not require the tuning parameters associated with the AD-method. However, this method requires substantial numerical effort and is not easily implemented in any general purpose software package, as it requires fundamental rewriting of the finite element code. Advanced general purpose FEM software is commonly used in the industry, as the lubrication problems usually encountered involve a multidisciplinary field, including thermal, structural, thermo-elastic and hydrodynamic simulations.
Hence, the chosen stabilization technique here is the artificial diffusion method (AD), as it can easily be implemented and only requires a slight modification to the coefficients in the general form PDE. In this method, the diffusion part in the convection-diffusion equation is slightly modified with an additional artificial diffusion term
in the convection-dominated part of the film:
Note that the solution obtained using this method should be examined carefully as a slightly modified PDE is solved instead of the original one. Moreover,
should not be so large as to introduce excessive damping, but should be minimal just to suppress the generated oscillations. Hence, an optimum value for
needs to be chosen. The artificial diffusion coefficient
is chosen as follows:
where
is a typical element size in the streamline direction and
is a constant that depends on the order of the elements that are used with
for linear elements and
for quadratic elements [
22]. In the present analysis, linear elements are used.
u and
k are respectively equivalent to the velocity and diffusion coefficient in a typical convection-diffusion equation and can be calculated as follows:
is an upwind function and can (after making an asymptotic approximation [
22]) be computed as follows:
where
is the cell Peclet number
. Due to the Boolean expressions,
becomes zero in the full film region and infinite in the cavitated region. Consequently, the upwind function
reduces to one in the cavitated region and zero in the full film region. Substituting Equation (
11) into Equation (
10) results in the following Reynolds equation:
This equation is strongly non-linear due to the included Boolean expressions. After discretization using finite elements, the system of non-linear equations is solved using a simple fixed-point iteration where the Boolean expressions are evaluated by means of the solution of the previous iteration, which then results in a linear system of equations.
The dependent variable
ξ and flow
are plotted in
Figure 2b after solving Equation (
14). The results are compared with another streamline stabilization technique (SUPG) in
Figure 2b from which it can be concluded that the results obtained using AD and SUPG are in close agreement.
Figure 2.
Dependent variable ξ and flow against the dimensionless length of the fluid domain, without (left) and with numerical stabilization. = 1, = 1 and ε = 0.4. (a) FEM solution of the 1D Reynolds equation without stabilization, showing oscillations in the convection-dominated cavitated region; (b) comparison of the artificial diffusion (AD) and streamline upwind Petrov-Galerkin (SUPG) stabilization methods, showing similar results of the pressure and mass fraction. The discontinuity of the flow is not yet minimized here.
Figure 2.
Dependent variable ξ and flow against the dimensionless length of the fluid domain, without (left) and with numerical stabilization. = 1, = 1 and ε = 0.4. (a) FEM solution of the 1D Reynolds equation without stabilization, showing oscillations in the convection-dominated cavitated region; (b) comparison of the artificial diffusion (AD) and streamline upwind Petrov-Galerkin (SUPG) stabilization methods, showing similar results of the pressure and mass fraction. The discontinuity of the flow is not yet minimized here.
Some discontinuity of flow at the reformation boundary remains, however, which should be continuous from the physical perspective. Minimization of this discontinuity can be obtained by choosing an optimum value for the transformation constant
. An attempt to resolve this challenge is by equating the flows at this boundary and working out using numerical differences; or:
where
and
stand for the flow in the cavitated and full film region, respectively. Substituting the proposed transformation (Equation (8a) and (8b)) into Equation (15b) and working out in terms of numerical differences gives:
where
and
are the film thickness and solution at this interface point. The partial derivative is approximated using the numerical difference between the values of point
r and downstream neighboring point
. In the cavitated region, the pressure is less than zero
, whereas in the full film region, the pressure is equal to or larger than zero
. According to this, a critical transformation constant
may be introduced, which complies with the following expression:
For values
close to
, the discontinuity at the reformation boundary was minimal, and faster convergence was achieved; see
Figure 3a. As can be observed,
depends on the local height at the reformation interface, which is initially unknown. However, after performing some numerical experiments, it was observed that in most cases,
is found to be very close to the maximum film height of the oil film. Hence, the maximum film height was used in the calculation of
.
With the dependence of
on
, Equation (
14) can now be simplified by suggesting
.
Note the absence of any Boolean functions in the pressure term. This optimized transformation results in fast convergence, as it is slightly less non-linear and, thus, more stable. In
Figure 3b, the mass fraction, film thickness, flow and pressure are plotted after solving Equation (
18). It is clear that the flow discontinuity is minimal now. Note that due to this chosen value of
, which is dependent on the local element size
, the flow discontinuity is effectively minimized by locally refining the mesh size near the reformation boundary.
Figure 3.
Distribution of mass fraction, film thickness, flow and pressure for
= 1 and
. (
a) Flow in the area near the reformation boundary using values close to the optimal transformation constant
. Note that the maximum film height was used for the calculation of
. (
b) Solution of the 1D Reynolds equation (Equation (
18)) using
, showing only minimum flow discontinuity.
Figure 3.
Distribution of mass fraction, film thickness, flow and pressure for
= 1 and
. (
a) Flow in the area near the reformation boundary using values close to the optimal transformation constant
. Note that the maximum film height was used for the calculation of
. (
b) Solution of the 1D Reynolds equation (Equation (
18)) using
, showing only minimum flow discontinuity.
This 1D cavitation algorithm has been verified for the full range of shaft eccentricity values and for a large range of mesh densities, for low to high numbers of degrees of freedom
.
Figure 4a gives a representation of the required number of iterations
and
, in order to obtain relative errors of
, as a function of
ε. As can be observed, the maximum number of iterations required is seven, which contributes as evidence for fast convergence. Typically, the computation time is within a few seconds on a quad core desktop computer.
It should be noted that if one only considers the pressure and/or the mass fraction profiles, it may seem that the solution is smooth enough. The streamline flow
, however, may exhibit oscillations due to the existence of steep pressure gradients, in particular at higher values for
ε. Of course, this means that the mesh size has to be chosen smaller. This problem is clearly exposed in
Figure 4b.
Figure 4c,d shows that the results obtained using our AD-stabilized cavitation algorithm are identical to "exact" results calculated by SUPG-stabilization, even for relatively high values of
ε. This comparison shows the numerical robustness of the cavitation algorithm for high
ε values.
Figure 4.
Verification and/or representation of the numerical stability of the cavitation model for the full range of shaft eccentricities. = 1. (a) and are associated with ε in order to obtain an optimum combination of accuracy and computational expense for the 1D model; (b) the influence of on the streamline flow distribution for . Note the oscillations in the solutions for a lower value of . (c) Comparison between pressure distributions obtained using the AD method with the SUPG method for relatively high eccentricity ratios. The results strictly follow each other. (d) Comparison between mass fraction distributions obtained using the AD method with the SUPG method. Even for high ε, minimal discontinuity is observed near the reformation boundary. Furthermore, excellent agreement exists between the results obtained using both methods.
Figure 4.
Verification and/or representation of the numerical stability of the cavitation model for the full range of shaft eccentricities. = 1. (a) and are associated with ε in order to obtain an optimum combination of accuracy and computational expense for the 1D model; (b) the influence of on the streamline flow distribution for . Note the oscillations in the solutions for a lower value of . (c) Comparison between pressure distributions obtained using the AD method with the SUPG method for relatively high eccentricity ratios. The results strictly follow each other. (d) Comparison between mass fraction distributions obtained using the AD method with the SUPG method. Even for high ε, minimal discontinuity is observed near the reformation boundary. Furthermore, excellent agreement exists between the results obtained using both methods.
To further validate our algorithm, the cavitation algorithm was used in several case studies for which there are reliable benchmark solutions in the literature. Giacopini
et al. [
23] developed a mass-conserving cavitation algorithm based on the concept of complementarity and successfully verified their model using several case studies with (semi)-analytical and numerical formulations. In the present paper, the proposed cavitation model will be adapted to three different case studies in order to test its numerical properties and finally verify the results with those of Giacopini
et al. [
23].
The first situation represents a simple journal bearing with an infinite width (see
Figure 5a). The dimensions and relevant operating conditions are given in
Figure 5. As can be observed, the film rupture and reformation boundary are accurately calculated. Excellent agreement is found between the predicted and reference pressure profiles.
The second situation is somewhat different, as the film thickness profile has a divergent-convergent shape (see
Figure 5b). As can be extracted from
Figure 5b, the film cavitates in the diverging region. Again, there is excellent accordance among both the predicted and reference results. Note that the diverging-converging shape of the film thickness can also be considered to be an idealization for situations involving surface texture.
Figure 5.
Comparisons between predictions of the presented method with Giacopini
et al. [
23] for an infinite width sinusoidal bearing. Operating conditions for the present case are [
23]:
mm,
mm,
Pa·s,
m/s and Boundary Condition 1 (BC1):
MPa. (
a) Comparison of the predicted pressure distributions with Giacopini
et al. [
23] for
. There is excellent agreement between the results. (
b) Comparison of the predicted pressure distributions with Giacopini
et al. [
23] for
. Again, excellent accordance between the results is observed.
Figure 5.
Comparisons between predictions of the presented method with Giacopini
et al. [
23] for an infinite width sinusoidal bearing. Operating conditions for the present case are [
23]:
mm,
mm,
Pa·s,
m/s and Boundary Condition 1 (BC1):
MPa. (
a) Comparison of the predicted pressure distributions with Giacopini
et al. [
23] for
. There is excellent agreement between the results. (
b) Comparison of the predicted pressure distributions with Giacopini
et al. [
23] for
. Again, excellent accordance between the results is observed.
Hence, the last situation is that of a non-convergent/parallel bearing with a single microtexture pocket near the inlet (see
Figure 6a). The reference dimensions and operating conditions are given in
Figure 6. For this case, Olver
et al. [
24] derived an analytical solution, which pointed out the existence of a region in which the film cavitates. Comparisons of the predicted pressure profile with those of the reference authors are provided in
Figure 6b in which the agreement is excellent.
Figure 6c compares the predicted fractional film content distribution with the reference results in which fair accordance is obtained. Note that the fractional film content in the work of Giacopini
et al. [
23] is modeled using compressibility and is thus modeled as the non-dimensional density, which is why we have used a different notation for the fractional film content for the results of the reference authors. However, in the cavitated region, the pressure is constant, and thus,
stands for the fractional film thickness.
Figure 6.
Bearing configuration and comparisons between predictions of the presented method with past literature. Operating conditions for the present case are [
23,
24]:
mm,
mm,
mm,
mm,
mm,
Pa·s,
m/s and
MPa. (
a) Schematic of a non-convergent/parallel bearing with a single microtexture pocket near the inlet. One surface is moving with velocity
U, while the opposing surface is kept stationary. (
b) Comparison of the predicted pressure distribution with Giacopini
et al. [
23] and the analytical solution of Olver
et al. [
24]. The results closely follow each other. (
c) Comparison of the predicted fractional film content distribution with Giacopini
et al. [
23]. There is fair accordance between the results.
Figure 6.
Bearing configuration and comparisons between predictions of the presented method with past literature. Operating conditions for the present case are [
23,
24]:
mm,
mm,
mm,
mm,
mm,
Pa·s,
m/s and
MPa. (
a) Schematic of a non-convergent/parallel bearing with a single microtexture pocket near the inlet. One surface is moving with velocity
U, while the opposing surface is kept stationary. (
b) Comparison of the predicted pressure distribution with Giacopini
et al. [
23] and the analytical solution of Olver
et al. [
24]. The results closely follow each other. (
c) Comparison of the predicted fractional film content distribution with Giacopini
et al. [
23]. There is fair accordance between the results.
2.2. 2D Stationary Situation: Crosswind Numerical Stabilization
In the previous section, the 1D cavitation algorithm was shown to be stable and robust and, moreover, produces results identical to the results found in the literature. Therefore, the algorithm will now be extended to a 2D cavitation algorithm. The extension of the stabilized 1D Reynolds equation (Equation (
18)) to a 2D finite length journal bearing reads:
For this case, the supply is over the full bearing length (BC1: ), and the pressure on the edges of the bearing is set equal to zero (BC2: ). Furthermore, a relatively coarse grid is used to show the numerical stability of the stabilization techniques used.
When Equation (
19) is solved without further stabilization, the distribution of the mass fraction is not smooth, and spikes occur at the edges of the bearing, as can be seen in
Figure 7a. This means that only applying streamline stabilization is not sufficient. Numerical stabilization is required in the crosswind direction (
Y-direction), as well as in order to smooth the solution of the flow in the cavitated region. In Hughes
et al. [
19], Codina [
22] and Tezduyar and Park [
25], for instance, methods have been studied to choose the crosswind artificial diffusion coefficient. In this study, the diffusion term in the
Y-component of the Reynolds equation is modified by adding an artificial diffusion term
:
In this study, the crosswind diffusion coefficient is chosen similar to
, but scaled relative to the angle between the flow solution gradient and flow direction. The crosswind artificial diffusion coefficient
is chosen as follows:
where δ is a very small number (order of magnitude 1e-10) to prevent numerical problems in areas where the gradients
and
are zero. Substituting this value for
in Equation (
20) results in the stationary cavitated-modified Reynolds equation for a 2D lubricating film:
A convergence analysis was performed from which it was concluded that an optimum combination of accuracy and the number of elements is obtained at 4100 (approximately 8050 linear elements). Relative errors of approximately are usually found within 10–15 iterations. Typically, the computation time is within 10 s on a quad core desktop computer.
Figure 7.
Mass fraction contours with and without crosswind numerical stabilization for = 1 and ε = 0.6. (a) Only streamline stabilization, i.e., showing spikes in the Y-direction near the edges; (b) non-linear crosswind stabilization suppresses the spikes.
Figure 7.
Mass fraction contours with and without crosswind numerical stabilization for = 1 and ε = 0.6. (a) Only streamline stabilization, i.e., showing spikes in the Y-direction near the edges; (b) non-linear crosswind stabilization suppresses the spikes.
Solving Equation (
22) using a typical PDE routine gives a reasonable solution, as the overshoot for the mass fraction distribution is almost suppressed and the sharp transition at the edge of the bearing is retained; see
Figure 7b. Several other non-linear crosswind numerical stabilization techniques have also been tested, but the one represented by Equation (
21) has been shown to be most stable and the fastest to converge.
The artificial diffusion term for the crosswind stabilization slightly changes the original Reynolds PDE. In order to see if the results after this modification are still accurate, our cavitation algorithm was compared with those from Yu
et al. [
26] for a fully submerged bearing. Yu transformed Elrod’s universal differential equation into a boundary integral equation by means of boundary element theory and compared their results with those obtained using a finite difference approach in which they found excellent accordance. Typical Dirichlet conditions (
) are imposed on all edges of the computational domain. The pressure and mass fraction distributions are compared in
Figure 8a,b, respectively, from which it is clear that the results closely follow each other. As mentioned earlier, the fractional film content in the full film region of the reference results is modeled using compressibility, which is the reason why the non-dimensional density slightly increases in that region.
Based on this comparison, it can safely be stated that the artificial diffusion terms have little influence on the overall solution accuracy, and thus, the AD-method may be used.
Figure 8.
Steady-state validation of the proposed 2D cavitation model with Yu
et al. [
26] for
= 1 and
ε = 0.6. The graphs are plotted at an axial location of
Y = 0.2 for the sake of comparison. (
a) Comparison of pressure distributions; (
b) comparison of mass fraction distributions.
Figure 8.
Steady-state validation of the proposed 2D cavitation model with Yu
et al. [
26] for
= 1 and
ε = 0.6. The graphs are plotted at an axial location of
Y = 0.2 for the sake of comparison. (
a) Comparison of pressure distributions; (
b) comparison of mass fraction distributions.