1. Introduction
Sliding friction under boundary lubrication has been studied for almost a century [
1,
2,
3,
4,
5]. In the boundary lubrication regime, the lubricant film is not sufficiently thick to separate the surfaces and solid-to-solid contact will occur. Under these conditions, primarily, the highest peaks (asperities) on the surfaces will come into contact. Therefore, the asperities are carrying the load locally, so on a microscale, the stresses exceed the yield of the material causing plastic flow even though the macroscopic pressure is well below the yield limit. This elastoplastic deformation of asperities has been regarded as one of the important sources of friction [
2]. Meanwhile, a solid layer is also generated in boundary lubrication and plays a crucial role in protecting the system against severe friction and wear. This layer consists of two separate layers, one produced by chemical reactions and one by the mechanical energy dissipated at the top layer of the bulk material (nanocrystalline (NC) layer) (see
Figure 1). The properties and composition of these layers are dominated by the lubricants used (mainly the additives package) and the conditions under which the system is running. Using this representation of the system in previous publications, wear rates were successfully predicted [
6,
7]. In these publications, mechanical properties available in the literature were used for both the NC layer and the tribofilm. However, the coefficient of friction was presumed known and constant. In this publication, the latter will be investigated in more detail and the main question to be answered is: “Can plastic deformation of the tribofilm and NC layer explain the coefficient of friction observed in boundary lubrication?”
It has been known for many years that different additives influence the tribological behavior of a system (the level of friction and wear). This can be explained by the fact that different additives will produce different tribofilms [
8] which tweak the contact status (contact pressure and deformation, real contact area, etc.) of asperities. The finite element method (FEM) is a commonly used approach in solving contact problems. Liu et al. [
9] analyzed the elastic-plastic contact of rough surfaces in line-contact problems. This work was extended by Etsion [
10] for point contacts. Furthermore, Jackson et al. [
11] developed a finite element model predicting the normal and tangential resisting forces of two sliding elastic, perfectly plastic frictionless spherical asperities. Mulvihill et al. [
12] improved this work by imposing greater interference depths and considering surface adhesion in the contact. However, it should be noted that performing FEM contact analysis is time consuming since a very fine mesh is needed in contact areas to ensure convergence and accurate results, while the domain needs to be large enough to avoid edge effects. In addition, the contact condition itself (no penetration of the two bodies) is not inherently incorporated to the FEM method and requires additional degrees of freedom (DOF) for a solution to be reached. Often, the penalty function is used, in which the magnitude of the contact stiffness is tuned using a Hertzian reference contact. While the obtained value may be true for the reference case, it is very possible that in different scenarios the values obtained do not hold.
In addition to FEM, which is governed by continuum mechanics, alternative options have been proposed to solve the contact process. Molecular dynamics (MD), for example, simulates the contact process at the atomic level. This method allows all atoms inside the calculation domain to move simultaneously, and interactions between these atoms are calculated by Newton’s law. It is thus possible to track the position information of each atom at a given time. Therefore, MD is particularly suitable for solving contact mechanics at the nanoscale [
13,
14,
15]. However, with increasing size and time scale, the computational cost will become unacceptably high and limit the application of MD in contact simulation. In recent decades, the discrete element method (DEM), as another alternative, has gained popularity in numerical tribology. DEM considers that the contact areas are composed of heterogeneous particles interacting with each other, governed by conservation and dynamics equations. DEM can calculate the behavior of detached particles efficiently and therefore is widely applied in simulating the third body behavior [
16,
17] and wear process [
18,
19]. DEM became even more versatile by combining with the cellular automata method: a series of dry friction problems between different materials were successfully simulated [
20,
21,
22]. However, properly choosing the size of single particles and defining the interaction force between them are a challenge [
23]. Besides, the application of DEM is also constrained by computational cost in large scale and a longer time period.
The fast Fourier transform (FFT) technique and semianalytical method (SAM) provide an alternative for solving elastic and elastoplastic contact more efficiently. Various problems including single and layered material contact have been solved by SAM [
24]. Also, techniques have been developed to accelerate the calculation and improve the accuracy. Polonsky and Keer [
25] proposed an iterative scheme by applying the conjugate gradient method. Liu et al. [
26] eliminated the periodic errors in regular FFT by introducing the discrete fast Fourier transform (DC-FFT) technique. However, the aforementioned works only handled purely elastic contacts. To solve elastoplastic contact problems, Jacq et al. [
27] presented a semianalytical method by considering plastic deformation as eigenstrains, based on Chiu’s results [
28,
29]. Recently, Wang et al. [
30] acquired stress and displacement fields of eigenstrains in two perfectly bonded layered halfspaces, making it possible to solve the elastoplastic contact of layered material.
In this paper, the sliding friction of a single asperity contact including a tribofilm and a nanocrystalline layer is solved by applying the DC-FFT technique and SAM based on the work in [
22]. Consequently, this work extends the model proposed by Boucly et al. [
31] which involved only homogeneous material, to a layered system. The plasticity in the layered structure is considered to follow the J2 flow theory [
32] and is solved by the method in reference [
30]. Green’s assumption on steady state sliding [
33] is applied: two asperities will not approach or separate over each other while sliding, e.g., a predefined separation of the two surfaces is given. To get an initial indication of the influence of the different aspects affecting friction, the effects of mechanical properties of the tribofilm (elastic modulus, Poisson’s ratio, yield strength, thickness), interference depth, and nanocrystalline layer are studied separately. The adhesion between tribofilms and damage to asperities are ignored, as the main goal of the study is to investigate the contribution of plastic deformation to friction.
2. Theory and Methodology
In this section, the general model is discussed first. The main backbone is a displacement-driven contact model for a layered elastoplastic system. This general model is used to investigate a single asperity contact with different mechanical properties.
2.1. Displacement-Driven Contact Model
First, a reference coordinate system is introduced, as shown in
Figure 2. For simplicity but without loss of generality, a contact of an elastoplastic object loading on a rigid flat is considered,where:
p is the contact pressure distribution built within the contact area;
ep is the plastic strain in the elastoplastic object formed due to contact stress;
ue is the surface displacement due to contact pressure, a function of the contact pressure distribution (p);
ur is the surface displacement due to residual plastic strain, a function of plastic strains (ep);
h0 is the initial surface separation relative to the initial undeformed geometry;
δz is the rigid body movement.
The initial geometry (h0) of contact objects (and their mechanical properties), together with a rigid body movement (δz), serves as input for the model. The model should be able to predict the contact pressure (p) and the subsurface plastic strains (ep).
In the whole domain in which contact and noncontact areas both exist, the following equations and conditions hold:
Outside the contact area:
Equations (1) and (2) indicate that in contact areas, surface separation must be zero (no penetration). In noncontact areas, however, surface separation should be greater than zero, which is shown in Equations (3) and (4).
Since the ultimate goal of the model is to find the pressure distribution and plastic strains that make Equations (1)–(4) hold, the exact expressions of ue(p) and ur(ep) should be built first. This will be described in the following subsections.
2.1.1. Elastic Displacement and Stress Fields
By employing Papkovich–Neuber potential and Fourier transformation, O’Sullivan and King [
34] derived the displacement and stress fields in a layered material:
with:
where
k = 1 indicates coating material and
k = 2 indicates substrate material.
A,
B, and
C are coefficients to be determined by boundary conditions (see [
34] for more details).
Once the frequency responses are acquired, the displacement and subsurface stress can then be linked to surface tractions by DC-FFT [
26]
where
qx is the surface traction in
x direction,
qy is the surface traction in y direction, and
p is the normal pressure. The tilde sign on top of variables stands for 2D Fourier transformation.
By letting qx and qy equal zero in Equation (7), the expressions of ue(p) can be acquired.
2.1.2. Residual Displacement and Stress Fields
The SAM was used in this work to evaluate the residual displacement and stress fields. In SAM, the plastic strains are considered as “eigenstrains”, while their influence on the domain as a whole is solved by a combination of analytical and numerical approaches. The method proposed recently by Wang et al. [
30] was used in this work and is described briefly below.
Firstly, a simple case is introduced, see
Figure 3 [
30]. A full space is composed of two halfspaces I and II. These two halfspaces are perfectly bonded, while eigenstrains exist in halfspace I.
The stress and displacement field in both halfspaces are solved. For example, the displacement field in halfspace I can be expressed as
Readers are referred to [
30] for more details on the influence matrices/coefficients.
However, this simple case solution is not instantly applicable to the model because in layered structure contact problems, a halfspace is needed instead of a full space, as shown in
Figure 4a. This halfspace is composed of a fully extended halfspace (the substrate) and a finite halfspace (the tribofilm, due to its finite thickness).
The principle of superposition states that for a given small deformation problem domain, if the state I is a solution to the fundamental elasticity equations with prescribed body forces F
I and surface tractions T
I, and state II is a solution to the fundamental equations with prescribed body forces F
II and surface tractions T
II, then state I + II will be a solution to the problem with body forces F
I + F
II and surface tractions T
I + T
II. Therefore, the layered structure contact problem can be split into two subproblems: an eigenstrain problem in a full space plus a set of imaginary surface tractions to make the aggregate solution satisfy the halfspace boundary conditions (surface traction free), as seen in
Figure 4b.
Note that the first subproblem is the eigenstrain problem in a full space, which can be solved by the method mentioned in Equation (9). The second subproblem, however, is a surface traction problem, which can be solved by Equations (7) and (8), by letting qx, qy, and p equal the imaginary surface tractions. By summing up the displacements caused by the eigenstrains and the imaginary stresses, the expressions of ur(ep) are acquired.
2.1.3. Model Route
With ue(p) and ur(ep) being expressed, the pressure distribution p and plastic strains ep are now explicitly linked to the inputs (rigid body movement δz and initial surface geometry h0) by Equations (1)–(4). This is in essence an M*N linear system. However, it should be noted that the subsurface stress generated by the surface contact pressure causes plastic strains. These plastic strains cause residual displacement and stresses, which in turn alter the geometry and change the surface contact pressure. In other words, p and ep are coupled. Thus, a direct solution is difficult to acquire.
Therefore, an iteration loop is proposed to address the problem. First, an initial status is set. The pressure and subsurface stress are solved first, followed by a radial return algorithm to determine plastic deformation for the current loop. Then, the residual displacement is calculated and surface geometry is updated. Afterwards, the pressure distribution is recalculated based on the new surface geometry. This loop will keep running till a convergence in pressure distribution is achieved (see
Figure 5). Note that in each iteration, an inner iteration (return mapping) is needed to map the stress back to yield surface and update plastic deformation. This process is shown in
Figure 6.
2.2. Single Asperity Sliding
In this work, the sliding asperity contact was idealized as a normal contact between two semispheres, following the work of Boucly [
31] (see
Figure 7). Using a semisphere to represent the asperity is a commonly adopted approach when studying a single asperity contact, as it allows a relatively simple calculation of the contact parameters. The two semispheres are aligned with the distance between two basis planes being held constant as
h, while the interference depth is
d0. Elastoplastic behavior of both tribofilm and substrate materials are considered, while adhesion between the surfaces is ignored.
The whole contact process is calculated in an incremental manner. In each incremental step, the corresponding rigid body movement is determined first, then the tangential and normal forces generated by the sliding contact, which are regarded as frictional and normal force, are calculated by the process proposed in
Section 2.1.
First, the whole sliding contact process is discretized into
n equally distributed incremental steps. In each of these incremental steps, the rigid body movement in the contact direction can be derived. In the
ith step, note that in the triangle
C2,original–
C1–
C2, the distance between the two centers of the semispheres is
C1C2, Therefore, the rigid body movement is
With
calculated, the contact force in each step
Fcontact,i can be calculated by the displacement-driven contact model. The frictional force and normal force in each step then can be acquired as tangential and vertical components of
Fcontact,i:
where
θ is the angle between
dΩ and the horizontal plane.
For the whole sliding process, the coefficient of friction (
COF) is defined as
Readers are referred to Boucly’s work [
31] for detailed expressions.
3. Results and Discussion
In this section, a tribosystem of a pair of steel asperities (25MnCr5) with a ZDDP tribofilm is set as a baseline, which is commonly seen as a soft-tribofilm and hard-substrate combination in industrial applications. The properties of the ZDDP film, steel substrate, and asperity radius were collected from the literature and are listed in
Table 1.
Next, a verification of displacement-driven contact model is presented, then the effects of different tribofilm properties on sliding friction are quantified.
3.1. Verification of Displacement-Driven Contact Model
The displacement-driven contact model proposed in
Section 2.1 was verified by an asperity indented on a coated flat plane. For simplicity without losing generality, the asperity was assumed rigid, while both materials of the coated flat plane showed elastic-perfectly plastic behavior. The material properties and contact conditions are listed below in
Table 2. Two different yield strengths of the coating material were used for comparison. The solution domain was meshed into an 80 × 80 × 80 grid (20 grid over the thickness direction of tribofilm). With a single element of size 6 × 6 × 6 nm, this resulted a calculation domain sized 480 × 480 × 480 nm, which was large enough to allow the plastic deformation to fully extend.
The results of the SAM model were verified by comparing the solutions with those from commercial FEM software (ABAQUS, from Dassault Systèmes, Vélizy-Villacoublay, France). The FEM model used four-node bilinear axisymmetric quadrilateral with full integration (type CAX4) elements. The element sizes varied from near the contact area (indicating the volume which has this fine mesh, 6 × 6 nm) to 100 × 100 nm in faraway areas. To limit the effect of boundary conditions in the FEM simulation, the modelling domain had to be at least 10 times larger than the contact zone. This gives a total of 55,214 elements in the FEM model.
A comparison of the results is presented in
Figure 8. The von Mises stress and equivalent plastic strain as a function of depth at the center of the contact are shown. Despite some minor differences, good agreement is observed.
Contour plots of the von Mises stresses and equivalent plastic strain in the
x-
z plane are shown in
Figure 9 and
Figure 10. The results show that plastic strains solely occur in the tribofilm due to its lower yield strength than steel. For the 500 MPa case, the plastic strain tends to concentrate near the bonding interface, while in the 800 MPa case, the plastic strain is more homogeneously distributed.
3.2. Single Asperity Sliding
Without considering adhesion effects, the sole mechanism behind friction in single asperity sliding is plastic deformation. The tangential force during the simulated sliding process is shown in
Figure 11 for both an elastic and an elastoplastic contact.
In the pure elastic deformation case, the friction force curve acts in a centrosymmetric manner, and thus the net frictional force is zero. However, when plastic deformation is involved, asymmetry of the tangential force can be observed. The reason for this change is that residual displacements modify the surface geometry and break the symmetry of the system. In other words, a certain amount of energy is dissipated during plastic deformation.
Therefore, anything that affects the plastic behavior of the system affects friction. In the following parts, effects of interference depth, tribofilm thickness, elastic/plastic properties of the tribofilm, and the presence of an NC layer on sliding friction are presented and discussed.
Also, the maximum calculated plastic strain in the tribofilm is introduced to measure the risk of tribofilm wear. As indicated in [
7] in single asperity sliding, most plastic strain occurs in the tribofilm. The higher the maximum plastic strain is, the more the tribofilm is worn.
3.2.1. Effects of Interference Depth
A series of interference depths were applied (20, 35, 50, and 65 nm), while other parameters were held constant (see
Table 1). The results are shown in
Figure 12, where it becomes clear that the tangential force increases with interference fit, which makes sense as more material is plastically deformed. This is also reflected by the increase in calculated coefficient of friction. It should be noted that the maximum plastic strain in the SAM calculations should not exceed 10% to ensure stable results [
37]. The increase in plastic deformation of the tribofilm also indicates that an increase in wear could be expected for the system under consideration, suggesting a relation between friction and wear.
3.2.2. Effects of Tribofilm Thickness
To investigate the effect of the thickness of the tribofilm, four thicknesses were applied in the model: 10, 60, 80, and 100 nm, respectively. The results are shown in
Figure 13.
The normal contact force decreases with thicker tribofilm, while softer tribofilms act like a cushion. The thicker the cushion is, the greater the effect will be. The friction increases with thicker tribofilm, which shows an almost linear relationship. This can be understood in terms of plastic deformation and energy dissipation. However, the relationship between the amount of plasticity and friction is highly nonlinear, showing a greater increase in plasticity than in friction.
3.2.3. Effects of Elastic Modulus
The elastic modulus of the tribofilms were chosen from 20 to 65 GPa, which refer to tribofilms softer and stiffer than ZDDP (e.g., the reference case, i.e., 35 GPa).
The results shown in
Figure 14 show that the frictional and normal forces increase with a stiffer tribofilm than expected. Also, a tribofilm with higher elastic modulus leads to a higher coefficient of friction. This is because with a higher elastic modulus, the tribofilm reaches its elastic limit at a lower strain level, which leads to a greater volume of plasticity. Additionally, a higher elastic modulus means more energy is needed for the same amount of plastic deformation. So for these two reasons, more energy is absorbed by the system, thus generating greater friction.
3.2.4. Effects of Tribofilm Yield Strength
In this part, the effect of the yield stress of the tribofilm on sliding friction is quantified. The yield stresses of tribofilms were set in a range from 350 to 800 MPa, which covers the tribofilms with higher and lower yield strengths than the ZDDP tribofilm.
From the results, it can be concluded that a tribofilm with a higher yield strength will cause a higher normal force, which is due to less plastic strain/displacement and thus a smaller contact area. Also, the coefficient of friction will decrease due to a higher yield strength of the tribofilm resulting from less plastic deformation. Therefore, the system will be affected less and show lower friction.
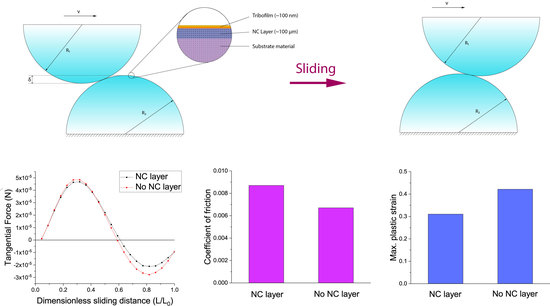
3.2.5. Effects of Presence of the NC Layer
In this subsection, the effect of the yield stress of the NC layer to sliding friction is quantified. In order to do so, the presence of a nanocrystalline layer is considered. The hardness of the nanocrystalline layer was taken from sample B in [
38], see
Figure 16.
With the presence of an NC layer, the frictional and normal contact forces increase. The reason for this effect is similar with a higher yield strength of the tribofilm leading to a higher normal contact force: the less strong NC layer allows higher plastic strain and displacement. Therefore, the geometry can better accommodate the contact deformation.
The coefficient of friction decreases with a higher yield strength of the NC layer. The relatively softer NC layer undergoes higher plastic strain and therefore dissipates more energy, which is consumed as friction. The maximum plastic strains in the tribofilm decrease with the presence of an NC layer because a softer NC layer makes it more possible for the plastic strain to extend downwards into the substrate. This makes the plastic strain accumulate less inside the tribofilm, which reduces the risk of tribofilm damage.
4. Conclusions
As in a previous study [
7] it was shown that mild wear in the boundary lubrication regime may very well be governed by the plastic deformation of the topmost material. The question is whether friction is also dominated by the mechanism. To answer this question, an elastoplastic coated single asperity sliding model was developed, with surface adhesion being ignored. The sliding process was solved in an incremental manner based on a displacement-driven contact model, accelerated by applying the conjugate gradient method (GCM) and DC-FFT technique. Analyses were carried out at various interference depths and tribofilm parameters, namely, thickness, elastic modulus, and yield strength. The main conclusion is that with adhesion being ignored, to obtain realistic values (~0.1) regarding the coefficient of friction, an unrealistically great interference depth would be needed and cause very high plastic strains. This would, however, in practice result in unrealistic values for wear. Thus, in layered boundary lubrication, other sources, e.g., surface adhesion, ploughing, and removal of asperities [
39,
40] may play a role in sliding friction. It is reported that with asperity failure included, the coefficient of friction is slightly higher than when the asperity failure ignored [
12]. These effects, however, are beyond the scope of this paper. Nevertheless, the following insights can be obtained from the results:
- (1)
The frictional force in a single asperity sliding is closely related to the plastic deformation of the asperities: greater plastic strain, higher sliding friction.
- (2)
Interference depth, tribofilm thickness, and the mechanical properties of the tribofilm will all affect the frictional force. Higher interference depth, thicker tribofilm, lower yield strength, and higher elastic modulus will contribute to a higher frictional force.
- (3)
The presence of a nanocrystalline layer will alter the behavior of the tribosystem. The presence of an NC layer will increase the coefficient of friction and ease the plastic strain accumulating in the tribofilm.