Contact Mechanics for Solids with Randomly Rough Surfaces and Plasticity

Abstract

We present experimental results for the elastic and plastic deformation of sandblasted polymer balls resulting from contacts with flat smooth steel and silica glass surfaces. Nearly symmetric, Gaussian-like height probability distributions were observed experimentally before and remarkably, also after the polymer balls were deformed plastically. For all the polymers studied we find that the surface roughness power spectra for large wavenumbers (short length scales) are nearly unchanged after squeezing the polymer balls against flat surfaces. We attribute this to non-uniform plastic flow processes at the micrometer length scale. The experimental data are analyzed using the Persson contact mechanics theory with plasticity and with finite-element method (FEM) calculations.

1. Introduction

Solids have surface roughness, which tremendously affects their contact mechanics and thereby a large number of interfacial phenomena including adhesion, friction, and the leakage of seals [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]. The nature of the contact between two solids also depends on their stress-strain relations. While real solids generally exhibit complex, non-linear viscoelastic properties, simple rheology models can be very useful to describe approximately and thus to rationalize the response of interfaces to external forces.

Two simple rheological models are the rigid-plastic and the elasto-plastic models. In the rigid-plastic model, see Figure 1a, a solid does not deform until the local stress reaches a critical value ${\sigma }_{\mathrm{P}}$ (the penetration hardness) at which point the solid starts to flow such that the contact stress always equals the penetration hardness. The rigid-plastic model does not account for the long-range elastic coupling between asperity contact regions, which is known to be crucial for most contact mechanical properties [16]. In the elasto-plastic model, see Figure 1b, a solid deforms non-locally as a linear elastic material until the local stress reaches the penetration hardness when it starts to flow such that the contact stress is always less than or equal to the penetration hardness.

Plastic deformation of most solids occurs in an approximately volume-conserving fashion. Predicting plastic flow is nevertheless a challenging topic, also because the induced flow often depends on the history of previous mechanical or thermal treatments of a given material [17]. For example, work-hardened and annealed metals tend to undergo different types of deformation, as shown schematically in Figure 2. In work-hardened metals, the plastic flow occurs such that the displaced material flows up around the indenter whereby it forms a raised portion close to the indenter surface. This behavior is reminiscent of that predicted by the model of rigid-plastic solids. The plastic response of highly annealed solids with an initial low concentration of dislocations is very different. When the indenter first begins to sink into the metal, the material adjacent to the indenter becomes work-hardened relative to the undeformed metal further away. As a result, when the indenter sinks in more deeply, it carries with it the surrounding material, which acts as an effectively enlarged indenter and deforms the metal adjacent to it. Consequently, the displaced metal always appears to be moving increasingly far away from the indenter itself. This results in a depression of the metal immediately adjacent to the indenter and a slight piling-up some distance away.

In addition to the complexity of the flow pattern occurring during plastic deformation, the stress needed to initiate plastic deformation may depend on the length scale, e.g., on the radius of curvature of the indenter. This is because the plastic flow in crystalline materials usually involves the motion of dislocations. A small volume may lack dislocations and dislocation generation centers. The fact that the penetration hardness of crystalline solids depends on the indenter size is well known and often observed when comparing the penetration hardness obtained using nano-indentation with those obtained in macroscopic hardness tests such as the Brinell hardness test.

In general, when two solids are squeezed together, the solids will be elastically deformed in some contact regions and plastically in some others. In the elastic contact regions, the pressure is below the material penetration hardness, while the pressure equals the penetration hardness in the plastically deformed contact regions. Due to the plastic deformation, the surface topography differs before and after the squeezing force is applied. If the external force is applied again, assuming the same relative orientation of the bodies, the solids will only deform elastically as long as the applied force does not exceed its original value.

It is useful to study how the elastic and plastic deformations change as we study the interface with increasing magnification $\zeta$. At small magnification, two nominally flat solids appear to be in complete contact. When we increase the magnification, we observe more surface roughness at a shorter length scale and the contact area decreases. As a result, the (mean) contact pressure in the perceived asperity contact regions increases with $\zeta$. Finally, the contact pressure may be so high as to plastically deform the solids. Whenever the surface roughness occurs on a wide range of length scales, there may be a wide range of long-wavelength roughness components, where the deformations are purely elastic, and a wide range of short-wavelength roughness components, which are fully removed by plastic flow, at least where contact takes place.

In Section 2, we present experimental results for the elastic and plastic deformation of sandblasted polymer balls resulting from contacts with flat smooth steel and silica glass surfaces. In Section 3, the experimental data are analyzed using the Persson contact mechanics theory with plasticity, and using finite element method (FEM) calculations. Section 4 contains the summary and conclusions.

2. Experiments

A set of experiments was performed, in which polymer spheres with sandblasted surfaces were squeezed against smooth steel and silica glass surfaces. The polymer balls of diameter $2.5\mathrm{cm}$ were made from polycarbonate (PC), nylon 66, ultra-high-molecular-weight polyethylene (UHMWPE), polypropylene (PP), and polytetrafluorethylene (PTFE). All the polymer balls were purchased from United States Plastic Corporation (www.usplastic.com).

The sandblasting was done with glass beads (spherical particles with smooth surfaces) of diameter ≈100 $\mathsf{\mu }$m. One set of balls was sandblasted for 2 min using 6 bar air pressure. For UHMWPE and PP we sandblasted the second set of balls using 6 min at 3 bar air pressure. The sandblasting nozzle was kept about 10 cm from a ball and the ball was rotated slowly so the sand beam uniformly exposed about 1/4 of the ball surface. This resulted in a surface area with uniform surface roughness.

A squeezing force $F_0\approx 465\pm 25\mathrm{N}$ was applied for 10 min, which induced small circular surface areas with diameters of approximately 3–6 mm (depending on the polymer), where the roughness of the spheres is smoothed by plastic flow. To determine the polymer indentation hardness, we also performed indentation experiments with a conical steel indenter with angle ${30}^{\circ }$ and the tip radius of curvature $0.4\mathrm{mm}$. In this case too the squeezing force $F_0\approx 465\pm 25\mathrm{N}$.

The polymers we use are not crosslinked. When exposed to small stresses they deform as viscoelastic solids. The deformations induced by large applied stresses involve moving polymer segments over energetic barriers which are so high that thermal fluctuations cannot return the polymer segments to its original configuration. This response could be denoted as nonlinear viscoelasticity, but here we will follow standard notation and denote it as polymer plasticity.

Unless otherwise stated, sandblasting took place under nominally identical conditions for two minutes for all polymer balls. The PP ball is most strongly effected (optically) by the sandblasting, while the polycarbonate is only weakly affected. It is also interesting to note that, before sandblasting, the PC ball had a very small surface roughness (see Figure 23 below), while all other polymer balls had a surface roughness of order ≈1 $\mathsf{\mu }$m. The relatively large surface roughness of these balls gives rise to light scattering. This may be the reason why all the balls except the PC ball appear gray or white, but even without surface roughness these semi-crystalline polymer balls may appear gray or white due to light scattering from the micrometer-sized crystalline domains with different orientation of the polymer chains. The small surface roughness of the PC ball may be related to the fact that PC is amorphous and hence relative homogeneous (like silica glass), while the other balls are semi-crystalline. Since the crystalline domains have different mechanical properties then the amorphous regions, inhomogeneous plastic flow processes occur during polishing or tumbling. This explains the large surface roughness (see Figure 3), which can scatter the light.

To study the influence of plastic flow on the contact mechanics we have first performed force relaxation experiments. In the experiments, the sandblasted polymer balls were confined between two flat steel surfaces. A squeezing force is applied by moving the upper steel plate slowly downwards (∼$1\mathrm{mm}$) for ≈$5\mathrm{s}$ until the squeezing force reach $F_0\approx 465\mathrm{N}$. After this the position of the steel plate is kept fixed, and the force $F\left(t\right)$ is studied as a function of time (force relaxation).

Figure 4 shows the force as a function of the logarithm of time. Note that for all the polymer balls, the force decays approximately logarithmically with time. This is due to thermally activated relaxation processes with microscopic processes having a broad distribution of activation energies. Thus, a plastic flow is due to the movement of molecular groups (here polymer segments) from one local potential minimum to another local minimum in configuration space. Immediately after applying the force $F_0$, the system is in a “critical state” where a small increase in the local stress gives rise to further plastic flow. This implies that some polymer segments are close to the top of the energy barrier separating it from another local minimum. Hence, thermal activation becomes important and results in the transfer of molecular segments over the energetic barriers. This results in a decrease in the force $F\left(t\right)\approx F_0[1-\kappa \ln \left(t\right)]$, where $\kappa \approx k_{\mathrm{B}}T/ϵ$ (see Ref. [1]).

In

Table 1. Information on (plastic) deformation experiments. Regular numbers relate to parallel plate geometries; those in round brackets to conical steel indenter. The diameter of the circular, plastically deformed region is denoted by $2r_0$. The (apparent) hardness is defined by ${\sigma }_{\mathrm{P}}=F_0/\left(\pi r_0^2\right)$, where $F_0\approx 465\mathrm{N}$ is the maximum applied squeezing force (load). The root-mean-square (rms) roughness amplitude is given for the sandblasted surfaces, and for the plastically deformed surfaces (in square brackets).

Polymer	$2{\mathit{r}}_0$ (mm)	${\mathit{\sigma }}_{\mathbf{P}}$ (MPa)	$1000\times \mathit{\kappa }$	rms ($\mathsf{\mu }$m)
PTFE	5.8 (3.0)	17 1(64)	29 (45)	3.0 [2.3]
UHMWPE	4.5 (2.7)	28 1(82)	47 (50)	4.1 [1.6]
PP	3.2 (2.2)	56 (117)	25 (50)	7.8 [4.1]
Nylon 66	3.2 (1.3)	56 (324)	19 (30)	2.0 [2.0]
PC	2.7 (1.5)	77 (258)	12 (43)	2.5 [1.6]

we give the diameter $2r_0$ of the circular plastically deformed region after squeezing the polymer ball against a flat steel surface with the force $F_0\approx 465\mathrm{N}$ for about 10 min. We also give the hardness ${\sigma }_{\mathrm{P}}^{*}=F_0/\left(\pi r_0^2\right)$. However, this is not the penetration hardness because it does not involve full plastic flow (see Figure 5 and below). We also measured the indentation hardness using a steel conical indenter with the angle ${30}^{\circ }$. The radius $r_0^{\prime }$ of the circular indentation and the penetration hardness ${\sigma }_{\mathrm{P}}=F_0/\left(\pi {r_0^{\prime }}^2\right)$ for the conical indenter is given in the round brackets in Table 1.

Note that the mentioned simple estimates for the indentation hardness using ${\sigma }_{\mathrm{P}}=F_0/\left(\pi r_0^2\right)$ are much higher for the conical indenter than for the flat steel or glass surfaces. This is due to the following effect: plastic deformations are very large when the conical indenter is used, because full plastic flow is expected near the indenter. In contrast, when the polymer sphere is squeezed against a flat surface, plastic flow occurs mainly in a small region below the center of the circular contact region where the stresses are highest (see Figure 5). This will, of course, influence the surface deformations in a region, which can be much larger than the size of the plastically deformed region. This explains why the apparent penetration hardness from the size of the deformed surface region is much smaller than the penetration hardness obtained from the conical indentation measurement.

As expected, for longer times, the force $F\left(t\right)$ decay logarithmically with time; the values of the slope parameter $\kappa$ are given in Table 1. We expect the hardness to be (approximately) proportional to the barrier height $ϵ$, and since $\kappa \approx k_{\mathrm{B}}T/ϵ$ we expect ${\sigma }_{\mathrm{P}}\sim 1/\kappa$. This relation is indeed approximately observed (see Table 1), except for PTFE.

We have studied the surface topography of the sandblasted balls before and after the plastic deformation. From the measured line-scans, we have calculated the one-dimensional (1D) surface roughness power spectra. The topography measurements were performed using Mitutoyo Portable Surface Roughness Measurement Surftest SJ-410 with a diamond tip with a radius of curvature of $R=1$$\mathsf{\mu }$m, and with a force of $F_{\mathrm{N}}=0.75\mathrm{mN}$. The scan length varied between 1 and $4\mathrm{mm}$ and the tip speed was v = $50\mathsf{\mu }$m/s.

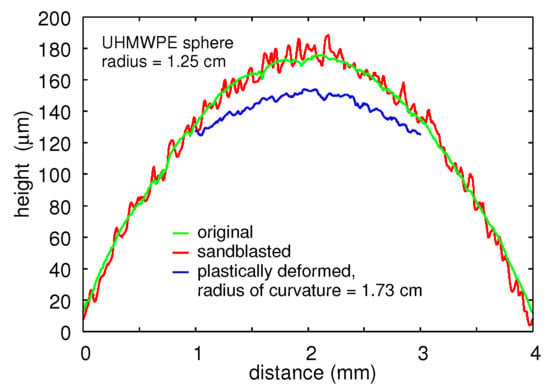
2.1. UHMWPE

Figure 6 shows the measured surface height of the untreated (new) UHMWPE sphere (green), after sandblasting the sphere (red), and in the plastically deformed surface area after squeezing the sphere with $F_0\approx 465\mathrm{N}$ for 10 min against a flat steel surface (blue). The radius of curvature of the original and the sandblasted sphere is ≈$1.25\mathrm{cm}$ which increases to ≈$1.73\mathrm{cm}$ in the plastically deformed region.

Figure 7 shows the surface height as a function of the distance along a straight line for the sandblasted sphere (red), and for the plastically deformed surface (blue), after removing the macroscopic curvature. Note that in spite of the big reduction in the roughness amplitude for the plastically deformed surface, there is no clear asymmetry between above and below the average surface line, e.g., the skewness is close to zero. This is even more clear in the probability distribution of surface heights shown in Figure 8, which is nearly Gaussian both before and after plastic deformation. This has important implications for the modeling of plastic flow (see below).

Figure 9 shows the 1D surface roughness power spectrum as a function of the wavenumber (log–log scale) for the sandblasted sphere (red), and from the plastically deformed surface area (blue). It is remarkable that the shortest wavelength roughness (with a wavelength of order ∼ 1 $\mathsf{\mu }$m) is nearly of the same magnitude before and after the plastic deformation, while the long wavelength roughness is strongly reduced. This could indicate that the plastic yield stress increases with decreasing length-scale or, more likely, it may be that the polymer flows at short length scales in an inhomogeneous way, generating a “universal” type of microscopic roughness, which is similar for the sandblasted and plastically deformed surfaces. Inhomogeneous plastic flow may be related to the size-dependency of the penetration hardness, so the two concepts may be related. Note that sandblasting is done with glass beads (spherical particles with smooth surfaces) of diameter ≈100 $\mathsf{\mu }$m. Their impact may result in locally similar plastic flow as when the UHMWPE sphere is squeezed against the flat steel surface. The inhomogeneous flow could result from inhomogeneities in the polymer matrix, e.g., small crystalline regions separated by disordered (amorphous) regions (see Figure 3 and Figure 10).

2.2. UHMWPE Repeat

In the experiments presented in Section 2.1, the UHMWPE ball was sandblasted for 2 min using 6 bar air pressure, and the plastically deformed surface was obtained by squeezing the ball against a flat steel surface for 10 min at the force $\approx 465\mathrm{N}$. Here, we present additional results where the UHMWPE ball was sandblasted for 6 min using 3 bar air pressure.

Figure 11 shows the surface height as a function of the distance along a straight line for the sandblasted UHMWPE sphere (red), and for the plastically deformed surface (blue) after removing the macroscopic curvature (radius of curvature of the sandblasted sphere is ≈$1.25\mathrm{cm}$, and ≈$1.60\mathrm{cm}$ in the plastically deformed region). Note that the amplitude of the roughness profile is smaller, both before and after the plastic deformation, than observed in Section 2.1. Nevertheless, the height profiles look approximately symmetric around the mid-line (dashed lines) indicating that the plastic flow reduces both the peak heights and the valley depth in a similar way. This is confirmed in the height probability distribution shown in Figure 12.

Figure 13 shows the 1D surface roughness power spectrum as a function of the wavenumber (log–log scale) for the sandblasted UHMWPE sphere (red), and from the plastically deformed surface area (blue). Again, the results are very similar to what was presented in Section 2.1 using different sandblasting conditions.

2.3. Nylon 66

We have performed measurements on a Nylon ball prepared under nominally identical conditions as for the UHMWPE-ball. Figure 14 shows the surface height probability distribution for the sandblasted Nylon surface (red) and the plastically deformed surface (blue). Nylon has a higher penetration hardness than the UHMWPE and the influence of plastic flow is much smaller than for the UHMWPE sphere. This is also clear from the surface roughness power spectrum shown in Figure 15, which is nearly the same for the sandblasted and plastically deformed balls.

2.4. Polypropylene (PP)

In optical pictures of the polymer spheres, the surface of the PP-sphere is most modified by the sandblasting. Figure 16 shows that the height probability distribution of the PP surface is strongly modified by plastic deformation. However, as for the UHMWPE-ball, it appears as if the roughness is reduced in the valleys as much as at the tops, and the skewness is nearly unchanged.

Figure 17 shows the 1D surface roughness power spectrum as a function of the wavenumber (log–log scale) for the sandblasted PP polymer sphere (red), and from the plastically deformed surface area (blue).

2.5. Polypropylene Repeat

In the experiments presented in Section 2.4 the PP ball was sandblasted for 2 min using 6 bar air pressure, and the plastically deformed surface was obtained by squeezing the ball against a flat steel surface for 10 min at the force $\approx 465\mathrm{N}$. Here we present additional results where the sandblasting was performed for 6 min using 3 bar air pressure.

After squeezing the ball against a flat silica glass surface for 10 min at the force $\approx 465\mathrm{N}$ we again find that the height profiles look approximately symmetric around the mid-line indicating that the plastic flow reduces both the peak heights and the valley depth in a similar way. This is confirmed in the height probability distribution shown in Figure 18.

Figure 19 shows the 1D surface roughness power spectrum as a function of the wavenumber (log–log scale) for the sandblasted PP sphere (red), and from the plastically deformed surface area (blue). Again the results are very similar to what was presented in Section 2.4 using different sandblasting conditions.

2.6. Polytetrafluorethylene (PTFE)

Figure 20 shows the surface height probability distribution of the sandblasted PTFE surface (red) and the plastically deformed surface (blue). In this case, the surface develops a small negative skewness upon plastic deformation, as expected in simple models of plastic flow, at least as long as the plastic deformations are small enough.

The surface roughness power spectrum is shown in Figure 21 Note that for large and small wavenumbers there is nearly no reduction in the surface roughness power spectrum upon plastic deformation.

2.7. Polycarbonate (PC)

Polycarbonate (PC) has the highest penetration hardness of all the studied polymers. Figure 22 shows the surface height probability distribution for the sandblasted PC surface (red), and the plastically deformed surface (blue). Note that while the sandblasted surface has a Gaussian height distribution, the plastically deformed surface develop a negative skewness as expected from simple models of plastic flow.

Figure 23 shows the 1D surface roughness power spectrum as a function of the wavenumber (log–log scale) for the sandblasted PC sphere (red), and from the plastically deformed surface area. The figure shows that the plastic deformation influence mostly the longer-wavelength roughness. In the figure, we show also the power spectrum of the original surface (green). The PC balls are much smoother than the other polymer balls, as reflected in the small magnitude of the power spectrum of the original surface.

3. Theory

3.1. Asperity Deformations and Contact Area

For contact between elastoplastic solids, the concept of magnification is very important. When the interface is observed at the magnification $\zeta$, only roughness with wavenumber $q<\zeta q_0$ is observed, where the $q_0$ is the smallest wavenumber. If the contact pressure in the asperity contact regions observed at the magnification $\zeta$ is below the penetration hardness ${\sigma }_{\mathrm{P}}$ the solid deforms elastically. However, when we increase the magnification, we observe more surface roughness at shorter length scales, and the contact area decreases. As a result, the contact pressure in the asperity contact regions increases as $\zeta$ increases. Finally, the contact pressure may be so high as to plastically deform the solid at a short length scale.

We will now analyze the data presented above using the Persson contact mechanics theory including plasticity. Using the surface roughness power spectra of the sandblasted polymer balls, and the penetration hardness obtained from the conical indenter, in Figure 24 we show the plastic contact area as a function of the logarithm of the wavenumber of the shortest wavelength roughness component included in the calculation. Note that when all the roughness is included for UHMWPE, PC, PP, and PTFE all the contact regions have yielded plastically so that $A/A_0=A_{\mathrm{pl}}/A_0=p/{\sigma }_{\mathrm{P}}$, but negligible plastic deformation occurs for Nylon 66, in agreement with the experiments. For the UHMWPE and PP balls, almost all the asperities have yielded plastically already for ${\log }_{10}q\approx 4.4$ (where q is in ${\mathrm{m}}^{-1}$), while for the PC and PTFE the asperity contacts are fully yielded plastically for considerable larger wavenumber. This is in qualitative agreement with the observation that the height probability distribution, which is determined mainly by the long wavelength roughness, is most modified for the UHMWPE and PP balls. However, the calculations differ in two respects from the experimental observations. First, from the calculation, one would expect the short wavelength roughness in the contact regions to be fully plastically flattened. This differs from the observation that the roughness power spectra for large wavenumbers are nearly unchanged in the nominal contact area. As explained before, this is either due to an increase in the penetration hardness with increasing wavenumber (or shorter length scales), or (more likely) due to non-uniform plastic flow processes which gives a “universal” type of roughness at short length scales. Secondly, for the UHMWPE and PP balls the surface roughness power spectrum is modified (reduced) by plastic flow already at the longest length scales while we predict no plastic flow until ${\log }_{10}q\approx 3.5$ for PP and ${\log }_{10}q\approx 4.0$ for UHMWPE. This may be due to some plastic deformation occurring already at pressures below the penetration hardness.

We note that including a dependency of the penetration hardness on the length scale (or magnification) is possible within the Persson contact mechanics approach (see Ref. [5]), and was in fact used in the study presented in Ref. [19]. It is less clear how to include strain hardening in this approach.

Let us discuss in more detail the nature of the surface roughness power spectrum for large wavenumber q. Figure 25a schematically shows a line scan of a randomly rough surface. Assume that the solid is squeezed against a rigid, perfectly flat countersurface. In the ideal (theoretical) model description, the surface roughness in the contact regions is perfectly smoothed, resulting in flat regions parallel to the external squeezing surface (see Figure 25b). However, in reality, our experiments show that the surface in the plastically flattened region still exhibits surface roughness at short length scales (see Figure 25c), which we attribute to inhomogeneous plastic flow at short length scale. In our applications, for UHMWPE at the highest magnification, the theory predicts that $A_{\mathrm{pl}}/A_0\approx 0.5$ (see Figure 24) so if the model case illustrated in Figure 25b would be correct, one expects a reduction in the power spectrum by a factor of ∼2 for the largest wavenumber. However, the actual reduction for the UHMWPE is only by a factor of ≈1.3, which illustrates that the short-wavelength roughness in the plastically deformed regions is nearly the same as in the original (not plastically deformed) surface.

That plastic flow occurs in a non-uniform way for crystalline (or semi-crystalline) materials, and hence generates surface roughness at short length scales, is well known [20,21], and results from the atomistic nature of solids where plastic flow involves defects or imperfections (e.g., nucleation centers for dislocations), and easy glide planes. Even for amorphous solids, computer simulations have shown that plastic flow at the length scale of a few nanometers occurs inhomogeneous even when the applied force field is uniform, e.g., a uniform applied shear stress [22]. The polymers used in our study are semi-crystalline, and since the crystalline domains are of micrometer size and have different mechanical properties than the amorphous regions, inhomogeneous flow on the microscale occurs during plastic flow. How plastic flow generate surface roughness for metallic-like crystalline solids was shown recently in a very interesting study by Venugopalan et al. [19].

3.2. Macroscopic Deformations and Surface Curvature

For the UHMWPE ball squeezed against the flat steel or silica glass surfaces, we have shown in Section 2.1 and Section 2.2 that the small flattened surface area formed due to plastic deformation is still curved (due to elastic rebound), but with a radius of curvature which is much larger than that of the original spherical ball. This increase in the radius is due to macroscopic plastic flow, i.e., not the microscopic plastic flow occurring at the asperity length-scale-level. If no plastic deformation would occurs, and if the ball is perfectly smooth, the maximum contact pressure would be given by the Hertz formula

$$p_{\mathrm{m}}=\frac{1}{\pi }{\left(\frac{6F_{\mathrm{N}}{E}^2}{R^2{(1-{\nu }^2)}^2}\right)}^{1/3},$$

(1)

and the average pressure $p_{\mathrm{av}}=2p_{\mathrm{m}}/3$. In the present case $R=1.25\mathrm{cm}$ and $E=1.25\mathrm{GPa}$ and using $\nu =0.4$ this gives $p_{\mathrm{m}}=107\mathrm{MPa}$ and $p_{\mathrm{av}}=71\mathrm{MPa}$. These stresses are similar to the penetration hardness of the UHMWPE, which we determine with the conical indenter to be ≈$82\mathrm{MPa}$. However, we will now show that the macroscopic plastic flow is mainly located in a region below the center of the flattened surface region.

For Hertz contact, the maximum shear stress occurs at a point located a distance of ≈$0.49a$ (where a is the Hertz contact radius) below the center of the circular contact area (see, e.g., Ref. [24]). Assuming the Von Mises yield criterion, the plastic flow will start at this point when the maximum surface stress $p_{\mathrm{m}}\approx 1.7{\sigma }_Y$, where ${\sigma }_Y$ is the yield stress under uniaxial tension. For the UHMWPE, ${\sigma }_Y\approx 24\mathrm{MPa}$ (see, e.g., Ref. [25]), i.e., about 1/3 of the penetration hardness ${\sigma }_P$ we measured using the conical indenter. Thus, incipient plastic flow will occur when $p_{\mathrm{m}}\approx 41\mathrm{MPa}$. We conclude that plastic flow will occur in some regions below the center of the flattened surface area. This will effectively reduce the stress at the surface when the ball is squeezed against the flat, and during contact, most of the surface region (assuming no surface roughness) would, in fact, be elastically deformed. We will substantiate these claims below with FEM calculations. However, the same is also clear from the fact that the flattened surface region (with radius 4.5 mm) after contact with the flat (steel or glass) surface is $278\%$ larger than the (projected) area (with radius 2.7 mm) resulting from the cone indenter; in the latter case, the plastic flow is complete and extends to the surface. In fact, it has been shown [26] that if the critical value of the indentation depth (also denoted interference or penetration) at the initiation of plasticity is denoted by ${\delta }_{\mathrm{c}}$, then the fully plastic contact will not occur until $\delta >110{\delta }_{\mathrm{c}}$. The fully plastic regime is reached when plastic deformation has completely engulfed the contact area at high loads, and where the pressure in the contact region is given by the material penetration hardness [27].

Consider the UHMWPE ball after the formation of a plastically flattened surface area, as a result of squeezing it against a flat rigid surface with the force $F\approx 465\mathrm{N}$. We have found in Section 2.1 (see Figure 6 andFigure 7) that the plastically flattened surface area is locally spherical with the radius of curvature $R^{*}\approx 1.73\mathrm{cm}$. To illustrate the accuracy of this statement, in Figure 26 we show, for another line scan (in an orthogonal direction), the measured height topography (red curve) and the topography after removing a quadratic function $c+x^2/\left(2R^{*}\right)$ with $R^{*}=1.73\mathrm{cm}$ (blue curve). Clearly, within the fluctuations resulting from the random surface roughness, the surface is perfectly spherical in the plastically deformed region.

Now, if we squeeze the ball again against the flat surface at the same location as the original contact, we expect only elastic deformations as long as the squeezing force is below $F\approx 465\mathrm{N}$. Thus, since the surface is locally spherical, we can apply Hertzian theory to estimate the maximum pressure, $p_{\mathrm{m}}$. Using (1) with $R=R^{*}=1.73\mathrm{cm}$ we get $p_{\mathrm{m}}=86\mathrm{MPa}$. This is roughly twice higher than the maximum stress $\approx 41\mathrm{MPa}$ expected in the contact region at the onset of plastic flow (see above). The explanation for this apparent discrepancy may be due to the residual stress field in the polymer due to the original plastic deformation (which may be of similar magnitude as the yield stress, but of opposite sign to that of the stress field resulting from the applied stress), and to strain hardening.

3.3. Finite-Element Analysis of Macroscopic Deformations

We have used the finite-element method (FEM, ABAQUS) to analyze the macroscopic deformations of a UHMWPE ball as it is squeezed against a flat surface. Both surfaces are smooth without microscopic roughness and the substrate is rigid. To reduce the computational effort we have used an axis-symmetric 2D model. In this model, the nodes on the axis of symmetry of the hemisphere are fixed in the radial direction, which does not greatly affect the solution owing to the Saint Venant’s principle. We applied an external load on the center of the rigid line and computed the resulting Von Mises stress and displacement. We used the Von Mises yielding criterion to determine the (local) transition from elastic to plastic deformation.

The same radius of the hemisphere, $R_c=1.25$ cm, and the same applied force of $F_0=465$ N were used as in the experiments. The Young’s modulus and Poisson’s ratio of the elastic sphere were held constant at 1.25 GPa and 0.4, respectively. UHMWPE resins exhibit significant strain hardening at large strain. This prompted us to use the relation between the physical stress $\sigma$ and strain shown in Figure 5b of Ref. [28].

We define the plastic strain ${ϵ}_p=ϵ-{ϵ}_Y$. Here ${ϵ}_Y=0.06237$ is the yielding strain, corresponding to a yield stress of ${\sigma }_Y=29.484\mathrm{MPa}$.

In our FE simulation, we use a mesh with four-node, bilinear axisymmetric, quadrilateral elements compromising a total of 6517 nodes, which is enough to allow the hemisphere’s curvature to be accurately described during the deformation. The rigid substrate is meshed with a two-node linear axisymmetric, rigid node. During the calculation, the fixed constraint was applied on the rigid lines, and a symmetry constraint was applied on the surrounding surface. The friction coefficient was set to 0. Finally, we use an iterative method to ensure the convergence of the nonlinear contact mechanics problem.

To test the accuracy of the calculation, we first compared the output for an elastic contact with the analytical solution of the ideal Hertzian contact. The difference between the numerical and analytical solution for the stress profile turned out to be less than $2\%$.

We now present some numerical results. Figure 27 shows the height profile of the original (undeformed) UHMWPE ball, and the height profile of the plastically deformed ball after removing the loading force $F_0$. While the employed stress–strain constitutive law leads to noticeably more plastic deformation than the measured one, the agreement can still be considered sufficiently qualitative to conclude that plastic flow takes place at the macroscopic level.

Figure 28 shows the Von Mises stress distribution inside the sphere. Note that the macroscopic plastic flow is mainly located in a region below the center of the flattened surface region. As a function of increasing load, initially, the ball will deform elastically, until the Von Mises stress, which is maximal inside the sphere some distance from the surface, reaches a critical value (the flow or yield stress), where plastic deformation starts occurring.

Figure 28 shows the intermediate annular plastic subregion between the edge of the elastic core and the outer front of the plastic region. The shape of the plastically deformed region is close to an ellipsoid with a flattened bottom and a larger radius in the radial direction than in the direction normal to the surface.

4. Summary and Conclusions

We have studied how the surface roughness of polymer balls is modified when the balls are squeezed against a flat (steel or silica glass) countersurface. We have used balls made of UHMWPE, PP, Nylon 66, PC and PTFE, which were sandblasted to produce randomly rough surfaces. The surface topography was studied before and after squeezing the balls against the flat surface, and the surface roughness power spectra were calculated for all the polymer balls. The influence of plastic flow on the (microscopic) surface roughness was analyzed using the Persson contact mechanics theory including plasticity, and the macroscopic plastic deformations inside the ball was studied using FEM calculations. The most important results are:

(1)

For all the polymer balls, which are semi-crystalline, the short scale (micrometer wavelength) surface roughness was nearly the same before and after the ball was squeezed against the flat surface. We attributed this to inhomogeneous plastic flow at short (micrometer) length scales.

(2)

For UHMWPE, we observed an elastic rebound of the plastically deformed surface region, resulting in a locally spherical surface, but with an increased curvature radius as compared to the undeformed ball radius; this result was reproduced by the FEM calculations.

(3)

The height probability distributions for many of the polymer balls show that the plastic flow reduces both the peak heights and valley depth in a similar way. This could be related to strain hardening, which may result in an upward (volume conserving) plastic flow relatively far away (here at the bottom of the valleys) from the asperity contact regions.