A Multi-Scale Simulation Approach to Investigate Local Contact Temperatures for Commercial Cu-Full and Cu-Free Brake Pads

Abstract

Copper from vehicles disc brakes is one main contributor of the total copper found in the environment. Therefore, the U.S. Environmental Protection Agency (EPA) and the automotive industries started the Copper-Free Brake Initiative. The pad friction material is essentially composed of a binder, fillers, reinforcing fibres and frictional additives. Copper and brass fibres are the most commonly used fibres in brake pads. There is a need to understand how the contact temperature distribution will change if copper-based fibres are changed to steel fibres. The aim of this work is, therefore, to investigate how this change could influence the local contact temperatures. This is done by developing a multi-scale simulation approach which combines cellular automaton, finite element analysis (FEA) and computational fluid dynamics (CFD) approaches with outputs from inertia brake dyno bench tests of Cu-full and Cu-free pads. FEA and thermal-CFD are used to set the pressure and the temperature boundary conditions of the cellular automaton. The outputs of dyno tests are used to calibrate FEA and CFD simulations. The results of the study show lower peaks in contact temperature and a more uniform temperature distribution for the Cu-free pad friction material.

1. Introduction

Both the brake pads and discs of disc brake systems wear during deceleration. Some of the wear will deposit on the ground and some will be airborne as particle emissions [1]. Copper from vehicle disc brakes is one of the main contributors of the total copper found in the environment and, therefore, regulations have been settled in the U.S. [2,3]. The Copper-Free Brake Initiative has, therefore, been started by Environmental Protection Agency (EPA) and automotive industries [4]. The aim of this initiative is to remove or consistently reduce the copper presence in friction materials (called Cu-full materials). A relatively new category of pads called “Cu-free” (or “eco-friendly”) has, therefore, been developed, contrary to “Cu-full” pads which contain copper [5,6,7,8,9,10,11,12]. In order to obtain Cu-free pads, Cu-fibres can be changed to steel fibres.

The friction material used in brake pads is essentially composed by a binder, frictional additives, fillers, and reinforcing fibres [13]. The binder is a polymer-based resin used to keep the component together, frictional additives are added to control the friction coefficient, fillers modify some properties of the material and reduce the costs, and fibres are responsible for carrying most of the load during braking, and they act as a support for the formation of the plateau from compacted wear debris. These fibres are usually made by metals and/or ceramics. Copper has a central role in the pad friction material since it helps to produce a nanocrystalline tribofilm on the pad contact surface which promotes smooth sliding conditions [14,15]. Menapace et al. [16] proposed that barite could be used instead of copper in pad friction materials to obtain a similar stable friction layer.

The change of material and distribution of fibres in the pad friction material will result in a change of the pad-to-disc contact situation. In particular, the local contact temperature of the friction material can be influenced. The contact temperature plays an important role because it changes the mechanical properties of the friction material. Moreover, high local temperatures could burn the resin that holds the fibres together and provoke a detachment of them, removing the capacity of the material to carry the load or changing the stability of the friction layer. In general, the heat transfer phenomena that occur at the contact interface are complex and unsteady.

Experiments with inertia dyno benches could be used to evaluate the temperature inside the pad friction material but it is difficult to evaluate the contact temperature at the interface with a thermocouple. Cristol-Bulthé et al. [17] used a high-speed infrared thermography to study the heat transfer phenomena that happen between disc and pads in brake system at a macro level. Additionally, there are some tribometer studies [18,19] with pins made of pad friction materials pressed against glass discs to study the formation and destruction of secondary plateau on the pin surface by recording with a camera. With the same approach, it is theoretically possible to evaluate the contact temperature using a thermo-camera, but the effect of the disc material and the design of brake caliper is lost. Numerical simulations, instead, could help to model the temperature at the contact interface in order to investigate it.

Disc brake simulations based on different approaches and scales could be conducted depending of what phenomena one wants to investigate. A thermal-computational fluid dynamics (CFD) approach [20,21,22] can be used to study cooling and finite element analysis (FEA) [23,24,25,26] to evaluate the contact pressure distribution and wear on macro-level. Cellular automaton (CA) approaches [27,28] could be used to evaluate the meso-contact temperature distribution of the components of the pad friction material. The objective here is to study the heterogeneity of the frictional material and evaluating the influence that changing the constituents’ causes. In the literature some authors [29,30,31,32] have developed methodologies to simulate the temperature in the pad-to-disc contact, including the friction layer, in the modelling and considering homogenous thermal properties for the friction material. Bode et al. [33] proposed a numerical model able to consider the heterogeneity of the friction material and, therefore, sensible to changes in the material composition. Furthermore, Goo [34] concluded that an infrared camera combined with FEA could be used to study the contact pressure and thermo-elastic behaviour. No studies known to the authors combined a macroscopic thermal simulation approach with a meso-scale approach to evaluate the influence of the copper in the friction material on the local contact temperature under the real macro-level boundary conditions.

The aim of this work is to investigate how the change from copper-based fibres to steel fibres in the pad friction material could influence the local contact temperature. This is done by developing a multi-scale simulation methodology which combine a CA approach to determine the meso-temperature distribution with outputs from inertia brake dyno bench tests, FEA and thermal-CFD, which are used to set the pressure and the temperature condition of the CA.

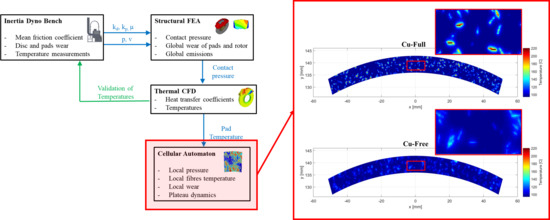
2. Methodology

The proposed simulation methodology to investigate mesoscopic pad temperature distribution is presented in Figure 1. First (Figure 1, box 1), the brake system and the load conditions are set in terms of system pressure (p) and velocity (v), and then inertia dyno bench tests are performed. The global coefficient of friction (µ) and the macro-temperature of the pads and disc are registered in real-time during the experiments. The specific wear rates (k_d and k_p) are determined by weighing the disc and pads before and after the tests. Second (Figure 1, box 2), a FEA with a wear sub-routine is performed, knowing the cycle and the specific wear rate from the dyno tests. The FEA outputs are the contact pressure distributions during braking, the global wear, and the particle emissions. Third (Figure 1, box 3), the computed contact pressure distributions are used as input in a one-way coupled thermal-CFD analysis where the macro-temperature of the brake components are computed. The temperature computed with the thermal-CFD analysis can be compared with the temperatures measured in the dyno bench tests. Fourth, and last (Figure 1, box 4), the global temperature and the contact pressure distributions coming from the thermal-CFD and the FEA are used as boundary conditions for the CA approach [35]. With the CA, the methodology goes into the meso-scales to compute the local pressure distribution, the local wear, the plateau dynamics, and the local contact temperature. Each step of the simulation methodology is described in detail below.

2.1. Inertia Dyno Bench

The inertia dyno bench used for the experimental test has been developed by Perricone et al. [36]. This setup is designed for tribology and airborne particles studies of disc brakes. The present work is not focused on particle emissions, so every detail regarding this are left out here. An illustration of the inertia dyno bench setup is shown in Figure 2. The setup consists of a clean chamber where the brake system is assembled. Air is taken from inside the climate-controlled room to ensure temperature and humidity conditions that are repeatable. The inlet flow rate is set to 850 m³/s, which corresponds to a velocity of about 5 m/s. Two walls inside the chamber entrance are used to avoid an excess of cooling on the side exposed to the air of the brake system. The disc axis is aligned with the inlet pipe axis. On the ceiling there are two outlets, one large outlet and one sampling pipe for the particle measurements.

The disc and pad temperatures are measured in real-time during testing by type-K thermocouples. The brake actuator controls the pressure in the hydraulic system and there is a torque feedback to regulate the pressure in order to obtain constant torque braking. The disc and pad wear are measured by weighting the components with a Sartorius MSE14202S balance (repeatability ±0.01 g, Otto-Brenner-Straße 20, Goettingen, Germany) before and after testing.

2.2. Structural FEA

The FEA approach presented by Riva et al. [37] is used in the present study to simulate the global contact pressure distribution and the wear of pads and disc. This approach has been verified by tests conducted in the inertia dyno bench setup described in the previous subsection. The simulation routine used to compute the wear after every brake event can be seen in Figure 3. The FE-model is setup in the Abaqus software package [38]. The brake system components are considered in the analysis: disc, bell, pads, pistons and caliper. The mesh of the brake system analysed is shown in Figure 4. The average mesh size is about 4 mm.

For every deceleration, a quasi-steady simulation is run to determine the contact pressure distribution between the pads and disc. To fix the system on the ground, a constraint is applied to the bell and to the caliper in correspondence to the fixing points. The load is applied in two steps. First, a pressure is applied to the pistons to simulate the braking force. Then, the pressure is kept, and the rotation is applied to the disc. Pressure and rotational speed are defined according to the braking cycle. To determine the wear, a constant pressure braking is considered for every braking and the wear is computed according to Archard′s wear law [39]:

$$\Delta h=k(p,v)·p·\Delta s$$

(1)

where h is the cell height in the axial direction, k is the specific wear the pad or disc, p is the contact pressure and Δs is the sliding distance. The specific wear values are kept constant during the cycle, and they are computed starting from the dyno test described in the previous sub-section knowing the mass worn:

$$k=\frac{\Delta m}{\rho ·\Delta s·F_N}$$

(2)

where Δm is the measure weight loss, ρ is the material density and F_N is the normal braking force. After the wear computation the nodes of the pads and the disc worn are moved, the mesh is update, and the next braking contact pressure can be computed until the last braking of the cycle.

2.3. Thermal-CFD

The thermal-CFD are performed with the commercial software StarCCM+ [40]. It consists in two different models: a steady state CFD model to compute the heat transfer coefficients (HTCs) and a transient thermal model to compute the brake system components temperature. The analysis is one-way coupled, which means that the CFD results are used as an input for the thermal model, but the temperature results from the thermal model do not affect the CFD analysis. In the CFD analysis the model consists in all the clean chamber of the dyno bench, which is shown in Figure 2.

The Reynold-averaged Navier–Stokes equations (RANS), together with the energy equations, are solved. A k-ε model is used for the turbulence [41]. Referring to Figure 2, the fluid dynamic boundary conditions are: velocity inlet at the entrance of the inlet pipe (Inlet), ambient pressure at the main outlet and outside the sampling pipe (outlets); a moving reference frame (MRF) technique is used to simulate the disc rotation. On all the brake system walls a temperature is imposed to calculate the HTCs, while all the other walls are considered adiabatic. The CFD simulation has run for three different velocities to obtain three different HTC maps as a function of disc rotating speed: 26–50–100 km/h.

In the thermal model, the heat transfer equation (Fourier equation) [42] is solved for all the brake system components: disc, bell, caliper, pads, pistons and fluid inside the caliper. The 3D heat transfer equation in Cartesian coordinates can be written as:

$$\rho c\frac{\partial T}{\partial t}=\frac{\partial }{\partial x}\left(k\frac{\partial T}{\partial x}\right)+\frac{\partial }{\partial y}\left(k\frac{\partial T}{\partial y}\right)+\frac{\partial }{\partial z}\left(k\frac{\partial T}{\partial z}\right)$$

(3)

where ρ, c, k are, respectively, the material density, specific heat and conductivity; T is the temperature. Conduction, convection and radiation between bodies are considered. Conduction is considered directly into the equation, while convection and radiation are considered setting an environment boundary condition on the brake system walls.

The HTCs obtained by the CFD analysis at different disc rotation speed are interpolated as a function of velocity and mapped on all brake components. Since the rotating parts are not rotating in the simulation, an average value is applied along the disc circumference to take the rotation into account. The brake power is applied to the pads and the disc starting from the contact pressure maps obtained in the FEA analysis described in the previous sub-section:

$$Q=\mu {\displaystyle \sum _{i=1}^N{P}_i}{A}_i{R}_{E_i}\omega$$

(4)

where µ is the global friction coefficient measured during the dyno bench tests, N is the number of cell, P_i is the local contact pressure defined for every cell, A_i is the cell area, R_Ei is the cell radius computed in the centroid of the cell and ω is the rotating speed. The total brake power can be split between disc and pads according to the following formula [43]:

$$\xi =\frac{Q_p}{Q_d+Q_p}=\frac{1}{1+\frac{S_d}{S_p}\sqrt{\frac{k_d{\rho }_d{c}_d}{k_p{\rho }_p{c}_p}}}$$

(5)

where the indices p and d represent pad and disc. The conductive heat transfer between pads and disc due to their contact is also considered. The result of the thermal analysis is the temperature history during the cycle on every brake component.

2.4. Cellular Automaton Approach

Starting from the work of Riva et al. [35], a CA approach has been further developed to include the local temperature computation on the friction material. The attention is focused on the friction material and the disc is considered as a flat surface which result in a shorter computational time to be able to predict the temperature of the friction material at the meso-scales. An overview of the simulation approach is shown in Figure 5. The CA simulation approach is the same used in [35] with the addition of a 3D grid for the thermal computation. The overall approach will be summarized here while the thermal computation will be described in detail below. First, the approach starts with some pre-process operations to define simulated pad portion and the grid, the time step, the material properties, the load, and the thermal boundary conditions. Second, the contact pressure is computed with a Winkler′s type elastic foundation model [44]. Third, the wear is computed using a generalization [45,46] of the Archard′s wear law [39]. Fourth, the plateau dynamics is simulated using some logical rules implemented in [35]. Fifth, and last, the temperature is computed on a 3D-grid solving the heat transfer equation with a finite difference method [42]. The simulation loop is repeated for every time step of every braking considered. At the end of the cycle, the output consists in the local pressure, local temperature, surface topography and plateau dynamics.

All the steps of the CA methodology are solved for a 2D mesh. A 3D grid is defined to compute the temperature in the friction material. Figure 6 shows the simulated pad area, the grid structure and the boundary conditions applied.

The simulated area is a band along the pad as represented in Figure 6. The heat transfer is set on the surface in contact with the disc, while on the back of the simulated portion the macro-temperature coming from the thermal-CFD analysis is set. The adiabatic condition is imposed on the inner and the outer sides. A symmetric boundary condition is applied on the upper and lower surfaces. Before every braking, the initial temperature is set as the initial braking temperature coming from the thermal-CFD analysis. The temperature is determined by the heat transfer (see Equation 3) which, in cylindrical coordinates, can be rewritten as:

$$\rho c\frac{\partial T}{\partial t}=\frac{1}{r}\frac{\partial }{\partial r}\left(\frac{1}{r}k\frac{\partial T}{\partial r}\right)+\frac{1}{r^2}\frac{\partial }{\partial \theta }\left(k\frac{\partial T}{\partial \theta }\right)+\frac{\partial }{\partial z}\left(k\frac{\partial T}{\partial z}\right)$$

(6)

where ρ, c, k are, respectively, the material density, specific heat and conductivity and T is the temperature. It is important to notice that k is not constant in space, since different material as friction material constituents are considered. To solve this equation, a finite difference method is applied with a forward time and central space finite difference [42]. Therefore, the time, first-degree space, and second-degree space derivatives in Equation (6) can be defined as follows:

$${\left(\frac{\partial T}{\partial t}\right)}_{i,j,k}^n=\frac{T_{i,j,k}^{n+1}-T_{i,j,k}^n}{\Delta t}$$

(7)

$${\left(\frac{\partial T}{\partial r}\right)}_{i,j,k}^n=\frac{T_{i+1,j,k}^n-T_{i-1,j,k}^n}{2\Delta r}$$

(8)

$${\left(\frac{{\partial }^{2}T}{\partial r^2}\right)}_{i,j,k}^n=\frac{T_{i+1,j,k}^n-2T_{i,j,k}^n+T_{i-1,j,k}^n}{\Delta r^2}$$

(9)

where ∆t is the time step, Δr is the radial distance between nodes and Tⁿ_i,j,k is the temperature of the (i,j,k) cell at the n instant. The simulation time step ∆t is set as the angular distance between two sub-domains divided by the disc rotational velocity:

$$\Delta t=\frac{b\Delta \theta }{\omega }$$

(10)

where b is the number of nodes in each sub-domain, Δθ is the angular distance between nodes, and ω is the rotational velocity. An illustration of the sub-domains are shown in Figure 7.

Since the disc rotational speed is changing during a braking, this approach considers an adaptive time step. To ensure the numerical stability, the minimum time step satisfies the CFL condition [42]:

$$\Delta t<0.17\Delta l^2\frac{\rho c}{k}$$

(11)

where Δl is the minimum distance between two nodes. The simulation time step is chosen to make the condition be respected for every type of material. Using this time step, the wear will be moved to the next sub-domain in the next time step.

3. Simulation Inputs

In the following subsections the inputs needed for the different simulation approaches are presented. Data about the brake system, pads, and disc are presented in Section 3.1. The urban driving cycle is presented in Section 3.2 and the inputs needed for the CA simulation in Section 3.3.

3.1. Disc Brake System

A typical front fixed caliper brake system used by a C-segment car is used in this study. The brake components are shown in Figure 8. The main characteristics of the car and the brake system are reported in

Table 1. Data of the car and its front left disc brake.

Name	Value
Wheel radius	361 mm
Rotor outer radius	171 mm
Rotor inner radius	92.2 mm
Rotor effective radius	136 mm
Pad surface area	7507 mm2
Cylinder diameters	4 × 22 mm

. The specific wear rate of pads and disc, which is obtained by the inertia dyno bench tests, for both the Cu-full and the Cu-free materials are reported in

Table 2. Specific wear rates (1/MPa).

Components	Cu-Full	Cu-Free
Pads	6.79 × 10−9	1.27 × 10−8
Disc	6.82 × 10−9	5.25 × 10−9

. The brake system consists of one brake disc, which is composed by a cast iron brake ring and a steel bell; one two-piece fixed aluminium caliper; two pads, each composed by friction material attached to a steel backplate; and four aluminium pistons.

3.2. Test Cycle

A test cycle to study wear and emissions of disc brakes during urban driving developed by Perricone et al. [47] is used in the present work. The list of braking of the test cycle considered is presented in

Table 3. Braking sequence during the test cycle [43].

Section	Initial Speed (km/h)	End Speed (km/h)	Initial Disc Temperature (°C)	Braking Deceleration (g)	Stops (#)
Cleaning	100	10	/	1.53	4
	100	20	/	1.53	2
	50	20	/	1.27	4
1.1	36	26	70	0.16	2
1.2	36	26	90	0.16	18
1.3	36	26	110	0.16	83
1.4	36	26	130	0.16	56
1.5	36	26	150	0.16	24
1.6	36	26	170	0.16	8
2.1	52	28	70	0.23	5
2.2	52	28	90	0.23	16
2.3	52	28	110	0.23	22
2.4	52	28	130	0.23	25
2.5	52	28	150	0.23	12
2.6	52	28	170	0.23	8
3.1	57	5	70	0.25	2
3.2	57	5	90	0.25	3
3.3	57	5	110	0.25	6
3.4	57	5	130	0.25	8
3.5	57	5	150	0.25	1
4.1	70	17	110	0.31	1
4.2	70	17	130	0.31	2
4.3	70	17	170	0.31	1
5.1	79	20	110	0.24	1

. The cycle is divided in six groups of braking and some sub-groups where the brake power does not change but the initial temperature changes. The “zero” group is called cleaning because it warms up the system and cleans the pad surface. All the cycles have been simulated in the FEA. Only the first two groups, cleaning and group one, are considered in the thermal-CFD analysis to reduce the computational time, which corresponds to about 1800 s of simulated cycle. In the CA, the cleaning braking and the 1.1–1.2 group braking are simulated to be able to evaluate one hard braking (100–10 km/h) and one soft braking (36–26 km/h).

3.3. CA Simulation Inputs

Two commercial pads have been evaluated: one Cu-full and one Cu-free material. The pad friction materials used in the FEA and thermal-CFD simulation have the same macroscopic geometry, but the wear and thermal properties differ. This results in different macroscopic contact pressure distributions and, therefore, temperatures that is used as boundary conditions in the CA. The differences of the pad friction materials in terms of fibre distribution are considered in the CA simulation. The initial surfaces and volumes are generated by using a Matlab script. The script has been developed to generate multiple fibres distributed in the thickness to obtain a 3D grid. The weight percentage of fibres used in the simulation for the two material are presented in

Table 4. Weight percentage of different fibre materials in the Cu-full and Cu-free pad friction materials.

Fibre Material	Cu-Full		Cu-Free
	wt %	Characteristic Length (µm)	wt %	Characteristic Length (µm)
Steel	<10	0.3	<25	0.3
Copper	<10	0.3	/	/
Brass	<10	0.3	/	/
Kevlar	<5	1.0	<5	1.0

. The 3D generated pad friction material according to Table 4 is shown in Figure 9. The fibre distribution is the same for every two layers in the thickness direction. This means that the fibres are contained into the plane formed by two layers and are not perpendicular to the planes themselves. The number of layers used in the simulation is 20 which corresponds to the number of nodes in z direction. The surface topography of the pad contact surface is randomly generated with the same script. As initial condition all the fibres are set at the maximum height, which means that they are potentially in contact, while the homogeneous material height is randomly set with a maximum depth of 50 µm. The initial surface topographies are shown in Figure 10, respectively, for Cu-full (above) and Cu-free (below).

The input parameters and the thermal properties used in the CA approach are shown respectively in

Table 5. Input parameters used in the CA simulation.

Name	Value
External radius simulated, re (mm)	0.1395
Internal radius simulated, ri (mm)	0.1325
No. of nodes in r direction	70
No. of nodes in θ direction	1000
No. of nodes in z direction	20
Radial distance between nodes, Δr (μm)	100
Radial distance between nodes, Δθ (μm)	100
Radial distance between nodes, Δz (μm)	100
Wear height of resin material, hm (μm)	20
Height of foundation, h (μm)	500

and

Table 6. Thermal properties of the pad friction materials.

Fibre Material	Density (kg/m3)	Specific Heat (J/(kg·K))	Thermal Conductivity (W/(m·K))
Steel	7800	460	49
Copper	8930	362	160
Brass	7900	372	100
Kevlar	1750	1000	0.4
Non-fibre (Cu-full)	2177	975	0.9
Non-fibre (Cu-free)	2357	838	2.3

. Although the copper in general contributes to increase the friction material conductivity, in this case the matrix of the Cu-free material is considerably more conductive.

4. Results

The results of the simulation methodology are presented in the following sections. The FEA results (Section 4.1) are used as an input for the CFD (Section 4.2) and CA (Section 4.3) simulations. The results of thermal-CFD analysis are used as input in the CA (Figure 1). One “hard” braking (brake event #4) during the cleaning section and one “soft” braking (brake event #30) at the end of Section 4.3 are presented in the results to show the temperature dependence at different brake conditions.

4.1. FEA Results

The contact pressure distributions during braking #4 and #30 are shown in Figure 11 for the pad on the external side of the caliper. The system fluid pressure for the two brake events are 2.0 and 1.0 MPa, respectively. The pressure on both the friction materials has a peak on the left chamfer edge. In general, the pressure distributions for the two friction materials are qualitatively similar.

The wear after braking #4 and #30 is shown in Figure 12. The wear is higher for the Cu-free material and the wear is higher on the edge of the chamfer due to the higher contact pressure. The cumulative mass lost during the test cycle is shown in Figure 13. The mass loss of the Cu-free pads-disc couple is higher compared to the one of the Cu-full pads-disc couple. In particular, the Cu-free pads loose around twice the mass of the Cu-full ones. Note that the wear is considerably higher during the cleaning block than the first block.

4.2. Thermal-CFD Results

A comparison between experimental and simulated results in the thermal-CFD analysis for the disc and the Cu-full pad temperatures is shown in Figure 14. The blue lines represent the disc temperature; the simulated disc temperature (continuous blue line) is aligned with the experimental one (dashed blue line) during all the braking considered. Note that only the cooling phase between the cleaning and the first group between around 200 and 500 s is underestimated. The simulated pad temperature (continuous red line) is in line with the experimental one (dashed red line) during the cleaning phase, but it is slightly underestimated during all the first group braking.

Figure 15 shows the comparison between the Cu-full and Cu-free friction material temperatures. Two measures are considered for each pad: the interface and 4 mm from the interface temperature. The interface temperatures (blue and red continuous lines) are similar. The Cu-full temperature 4 mm from the interface (dashed red line) is colder than the Cu-free one (blue dashed line).

4.3. CA Results

The simulated mean temperatures for the Cu-full and Cu-free pads during the cleaning section of the test cycle is shown in Figure 16 and for Sections 1.1–1.2 in Figure 17. The temperature at the back of the simulated volume is higher for the Cu-free material due to the higher diffusivity of the Cu-free material itself. The Cu-free contact temperature starts from a lower value and becomes higher compared to the Cu-full one.

In Figure 18 and Figure 19 the temperature distribution at the contact interface is shown for the Cu-full (upper) and the Cu-free (lower) pads. Note that the Cu-full friction material has relatively higher temperature peaks than the Cu-free friction material which has a more uniform distribution.

The percentage of secondary plateaus on the pad surface is around 7% for the Cu-full material and 10% for the Cu-free material after brake event #4. After brake event #30, the percentage secondary plateau on the contact surface is around 6% and 13% for Cu-full and Cu-free material, respectively. The distributions of fibres and secondary plateaus after brake event #4 and #30 are shown in Figure 20 and Figure 21.

5. Discussion

The higher peak in contact pressure for the Cu-full material (Figure 11) could be explained by the lower wear (Figure 12) which makes it harder to run-in the contact surfaces. The Cu-free pad wear more the Cu-free and is also more aggressive to the disc (Figure 13). This behaviour is considered in the CA simulation since more wear gives a higher possibility to build secondary plateaus on the pad surface. Figure 20 and Figure 21 confirm this higher secondary plateau formation on the Cu-free material in both brake event #4 and #30. Secondary plateau formation is higher in braking #30 which is the lower power brake event. This could be explained by that a higher contact pressure results in a higher amount of wear but also in a higher wear of the secondary plateaus created. This is in line with the work presented by Wahlström et al. [31] who conducted a factorial design to numerically study the effects of brake pad properties on friction and emissions and concluded that the there is a trade-off that depends on the specific wear rate of the contact plateaus between obtaining a sufficiently high stable friction and low emissions.

The results of the thermal-CFD show that the simulated pads temperatures are slightly underestimated compared to the measured one during the low power braking (first group of braking in Table 3). The difference is about 20 degrees, which is not so highly considered in that the changing of the temperature is very sensitive to changes in the measurement position of the thermocouple inside the pad friction material. The main cause could be the velocities chosen for the CFD analysis. Choosing velocities closer to the braking considered could increase the precision in the HTC′s computation and the temperature estimation. Referring to Figure 15, the higher temperature at the interface of the Cu-full material could be explained by the lower conductivity/diffusivity. Lower diffusivity means slower heat propagation inside the material, which leads to a higher temperature at the contact interface where the friction power is generated. It must be considered that, according to Equation 5, the lower diffusivity means lower friction power goes into the pad, if the total braking power is the same. This means that the higher braking power inside the Cu-free pad is not enough to have a higher contact temperature and the lower diffusivity of the Cu-full material is the dominant effect. This behaviour is also confirmed by the CA analysis (Figure 18 and Figure 19) where the mean contact temperature is higher for the Cu-full material. In the CA results it is also possible to notice that the contact temperature during the cleaning braking is decreasing at the end of the braking. This can be explained considering that the final velocity of the braking is low (10 kph) and this results in low braking power at the end of the deceleration. Therefore, the braking power could be lower than the heat transferred into the thickness of the pad. This effect is not visible in the low-power braking.

It should be noted that there is a difference in the contact interface temperature computation between thermal-CFD and CA analysis. First, the contact interface in the thermal-CFD analysis is relative at the centroid of the first cell, while in the CA it is related to the first node directly in contact. Second, the material is considered as homogeneous on the global scale, but not in the meso-scale, which is considered in the CA simulation. This leads to different contact condition and heat propagation. Different mean contact temperatures are also followed by different temperature distribution. These different temperature distributions at the contact interface between the two materials could be explained by the different diffusivity of the two materials. Although the Cu-free material does not have Cu fibres, which, in general, contributes to the increase in the conductivity of the material, the homogeneous fraction of the Cu-free material is more conductive, and the fibres percentage is slightly higher. A higher fibre percentage, coupled with higher specific wear rate of the Cu-free material, brings also to more secondary plateaus formation as mentioned in the previous paragraph. The secondary plateaus are built up by the wear of pad and disc together. Since the disc conduction higher compared to the pad, the secondary plateaus conduction will contribute to an increase in the conductivity of the friction material at the contact interface. The highest peaks in both the materials are in correspondence of the aramid fibres, which are the components with the lowest conductivity, even lower than the homogeneous material as modelled in the simulation.

Wahlström et al. [28] used a CA approach to simulate the temperature distribution at the interface. The results show higher temperatures around the fibres, in agreement with what found in the presented work. Since a constant sliding speed and pressure has been considered in their work, the secondary plateaus had time to build up and it helps the temperature to be distributed on all the contact surface. Moreover, no considerably different peak temperatures are visible on the pad surface, because the material properties are homogeneous, and the peak of temperature depends just by the contact pressure. Wahlström [30] also applied the same methodology to compared measured and simulated friction, wear and particle emission in a repeated braking test. The contact temperature result shows again peaks in correspondence of the fibres which is in line with the present study. Considering higher braking power with higher contact pressure, the secondary plateaus growth is higher, and it helps to obtain a more uniform temperature distribution. The same effect is also caused by the homogeneity of the friction material in terms of thermal properties, which gives to the homogenous component a higher diffusivity. Österle et al. [14] found that the copper fibres act as a primary contact sites in a similar way as steel fibres. This is aligned with what found here in terms of temperature distribution, which presents some peaks on the same order on steel, brass, and copper fibres. They can be distinguished, instead, by aramid fibres, which, as said, show a much higher peak of temperature due to the lower conductivity/diffusivity. Menapace et al. [15] investigated, with a pin-on-disc tribometer, a copper free material like the one considered in this study. They confirmed the importance of barite in the formation of friction layers (secondary plateaus) ensuring stability of friction coefficients and temperature evolution. This can be correlated with the higher secondary plateau’s formation on the Cu-free material, which has barite in the homogeneous material modelled.

6. Conclusions

A multi-scale simulation approach to predict the contact temperature distribution in disc brakes has been developed. This was done by combining three different simulation tools: a structural FEA, a thermal-CFD and a CA approach. Results from dyno bench tests are used as input to the macroscale simulations (FEA and thermal-CFD) which outputs are used as boundary conditions for the mesoscale approach (CA). One Cu-full and one Cu-free commercial brake pad were studied under urban driving conditions with the developed methodology. The following conclusions about local contact temperature can be drawn from the results of the present study:

(1)

The peaks in surface temperatures are considerably higher for the Cu-full pad friction material;

(2)

The surface temperature distribution is more uniform for the Cu-free pad friction material; and

(3)

The influence of copper-based fibres does not seem to have a significant impact on the local pad surface temperature.

The model to describe the pad friction material can be expanded to include more details on its constituents in the future. Moreover, wear and mechanical properties could be introduced for each component of the pad friction material in the same way as has been done for the thermal properties.