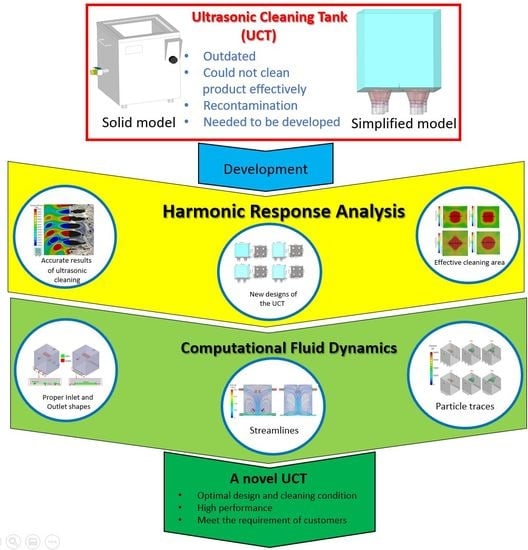
A Novel Ultrasonic Cleaning Tank Developed by Harmonic Response Analysis and Computational Fluid Dynamics

Abstract

The manufacturer of an ultrasonic cleaning tank (UCT) received advise from a customer to seek the cause to why the UCT could not clean their products effectively and develop a novel UCT to replace the conventional model. This UCT had a capacity of 10 L, a frequency of 28 kHz, four horn transducers, and a total power of 200 W. To resolve that problem and respond to customers’ needs, we presented new methods to develop the UCT using the harmonic response analysis (HRA) and computational fluid dynamics (CFD) to simulate the cleaning process which occurred within the UCT based on the actual conditions. Results from the HRA showed that the acoustic pressure in a problematic UCT was low, resulting in a smaller cleaning area, which was consistent with the results from the foil corrosion test, and thus caused the cleaning process to be ineffective. We developed a novel UCT with improved effectiveness by adjusting the design and adding a water circulation system. From the HRA, we were able to design the dimensions of the UTC and position of the transducer to be suitable to increase the acoustic pressure and cleaning area. CFD results enabled us to design proper inlet and outlet shapes, as well as simulate the water flow behavior to find the optimal cleaning condition so the novel UCT had a water circulation system that could eliminate the excess particles.

1. Introduction

Ultrasonic cleaning is one of the vital manufacturing processes in various production industries, e.g., rubber, food, electronics, oil, and others, especially jewelry [1,2], as Thailand is one of the world’s most important production bases [3]. In the jewelry industry, the shine and gloss of the goods are one of the highest concerns. Particles left from the machining and assembling process, the two main steps in the manufacturing process, could adhere to the products’ surfaces and cause dullness so it must be cleaned. The machining process consists of using machines to cut, scrub, wipe, and polish raw materials until they are in the small sizes and shapes required by the designer. Meanwhile, the assembling process is the process of bringing the small pieces resulting from the machining process together into larger, more sophisticated designs by special welding or adhering methods. It is the machining and assembling processes that causes miniscule particles as tiny as 10–150 micrometer to form. These particles must be washed away because, if not properly eliminated, by the end of the production line the jewelry’s surface will be uneven, causing it to lose its shine, charm, and trade value. At the present, ultrasonic cleaning is extremely popular among manufacturers for many reasons. The cost is low, it can clean bulks of goods within a short period, cleanse many types and sizes of unwanted particles, and clean products with complex designs or items with nooks and crannies scattered along the surface. The ultrasonic cleaning performance in a factory depends on the ultrasonic cleaning tank (UCT) and cleaning conditions, which are carefully designed by its manufacturer to suit the demands of each customer in specific industries for the highest efficiency. Therefore, it could be regarded as a great challenge for commercial UCT producers to design and manufacture high quality machines to be used in an industrial scale.

One highly necessary requirement for developing good UCTs is the knowledge about factors that affect the cleaning process. From research, we learned that the cleaning process happens when small bubbles collapse, causing a liquid jet to collide with and remove particles from the material’s surface. This is called the “cavitation effect” which is directly relevant with the acoustic pressure within the UTC. Effective cleaning occurs when the acoustic pressure intensity is appropriate with the size and type of material that the cleaner wants to remove. Factors that affect cavitation in the UTC are the cleaning fluid, temperature, standing wave, power, sonification time, and frequency [1,4,5]. When the frequency intensifies, the radius, pressure, and energy of bubbles decreases, also lessening the cavitation intensity as well [6]. When the power intensifies, the density of cavitation bubbles increases, collapses sooner, and the liquid-jet speed is faster [7,8]. The concentration of the solvent and surfactant in cleaning fluids also directly affect the cavitation that occurs in the UTC. Therefore, increasing or decreasing the solvent and surfactant’s concentration level affects the cleaning performance in the UCT [9,10,11,12]. In the case which cleaning fluids flow in the UCT, when the flow rate increases, the bubble collapsing rate drops along with the cavitation [13]. The transducers’ position also affects cleaning performance; if the transducers are placed in a suitable position, the cleaning performance will be high [14,15,16,17,18,19]. In order to design a UCT with high cleaning performance, computer simulation was applied to find the cause of why the UCT in this industrial factory was not cleaning properly. Once the simulation results were analyzed, other than sourcing the cause of the problem, we were also able to apply the findings to develop a new UCT with enhanced cleaning performance compared to the conventional model [17,18,19]. From the mentioned researches, it was indicated that highly efficient cleaning comes from UCTs that were well designed and tailored to cleaning conditions suitable to what particles must be cleaned. Computer simulation is an appropriate method used to design efficient UCTs that truly respond to the user’s demands.

This study was a collaboration between the authors and the manufacturing company with the objective to develop a novel UCT model for jewelry factories to replace the conventional model that was outdated and inconvenient for actual use. From the customer’s experience, when they used the conventional model, sometimes it cleaned the products well, but sometimes it did not, forcing them to repeat the process many times. However, after cleaning the product many times, it became even more contaminated. The authors anticipated that this occurrence may be caused by an unsuitable acoustic pressure inside the UCT, as well as recontamination caused by repetitively cleaning the item while the particles still remained inside the tank, thus reattaching to the surface. This problem could be solved by developing a novel UCT using both harmonic response analysis (HRA) and computational fluid dynamics (CFD) including methodology in the computer simulation. This article reports the success of solving this problem. The problem was that there had been no research on using the HRA and CFD to develop UCTs to match the needs of commercial users before. To conclude, we present a completely new, modern approach to solve actual obstacles found in the industrial sector.

2. Theoretical Background

The cavitation effect occurs when the piezoelectric transducer vibrates quickly, causing ultrasonic waves to enter the cleaning fluid. Changing phases between the lowest and the highest pressure causes small bubbles called “cavitation bubbles” to occur, which shrink and expand alternatively in a cycle according to the changing pressure. Once the pressure inside the bubble is lesser than the pressure outside, the bubble will quickly collapse, causing a liquid jet with a speed of approximately 200 m/s [20] to collide with the excess particles or contaminants on the product surface, resulting in the cleaning process [20]. To explain the cavitation occurrence, most studies used acoustic pressure that occurs inside the UCT using Equation (1) [17,18,19,21].

$$\nabla \cdot (\frac{1}{{\rho }_f}\nabla \cdot p)-\frac{{\omega }^2}{{\rho }_f{c}^2}p=0$$

(1)

2.1. Harmonic Response Analysis (HRA)

Generally, the HRA is used to find the structural response of solid materials towards loads that change according to time as in sinusoidal waves [22]. It was only recently that the HRA applied to calculate the acoustic pressure and position where cavitation occurs in industrial UCTs with high accuracy, thus showing that the position where the highest and lowest acoustic pressure occur is where the cavitation is the most intense. Simulation results were highly coherent with the foil corrosion test [17,18,19]. When designing UCTs, it is highly necessary to correctly calculate the acoustic pressure. In this research, we implemented the HRA in the ANSYS software 19.1, using the same successful methodology as in [17,18,19]. Calculating the acoustic pressure using the HRA may be explained as follows;

When electric currents were applied to the PZT4 transducer, it would vibrate at a frequency of 28 kHz. The transducers’ vibration caused the tank’s wall (made from stainless steel) to vibrate, which caused ultrasonic waves to form acoustic pressure in the water, eventually making cavitation occur. As for the finite element method, we may consider the UCT to consist of 3 material domains and 2 interfaces. The three material domains were the PZT4 domain, which caused the vibrations, the solid domain, which is the UCT’s wall and other hard structures made from either aluminum alloy or stainless steel, and the water domain, which is the cleaning fluid or solutions with surfactant mixed into it for cleaning purposes. The two interfaces were solid/fluid and PZT4/solid interfaces which were the connections in each domain and are highlighted in red lines in Figure 1, which display the material domains and interfaces used in calculation. The reason why they must be separated into domains was because the finite element equation for calculating the {u} in each domain and interface were different.

In PZT4 domain and PZT/solid interfaces, the vibrations of piezoelectric material occur from coupling due to structure and electric properties. When a voltage was applied to the piezoelectric, it would vibrate and cause a displacement vector {u} as in Equation (2) [23].

$$\left(\begin{array}{cc}{M}_{uu}& 0\\ 0& 0\end{array}\right)\left\{\begin{array}{c}\ddot{u}\\ \ddot{V}\end{array}\right\}+\left(\begin{array}{cc}{C}_{uu}& 0\\ 0& -C_{vv}\end{array}\right)\left\{\begin{array}{c}\dot{u}\\ \dot{V}\end{array}\right\}+\left(\begin{array}{cc}{K}_{uu}& K_{uv}\\ K_{uv}& -K_{vv}\end{array}\right)\left\{\begin{array}{c}u\\ V\end{array}\right\}=\left\{\begin{array}{c}F\\ Q\end{array}\right\}$$

(2)

In the solid domain, {u} from Equation (2) would be transferred to this domain and cause consistent vibrations to create ultrasonic waves the are transferred to the water domain. The finite element equation for the solid domain could be represented in Equation (3) [22].

$$[M]\left\{\ddot{u}\right\}+\left[\mathrm{C}\right]\{\dot{u}\}+\left[\mathrm{K}\right]\{u\}=\left\{F\right\}$$

(3)

Afterwards, the acoustic waves then move to the solid/fluid interface, or from the tank’s wall to the water {u}, this area can be calculated using Equation (4) [24].

$$\left(-{\omega }^2\left(\begin{array}{cc}{M}_S& 0\\ {\rho }_f{R}^T& M_F\end{array}\right)+j\omega \left(\begin{array}{cc}{C}_S& 0\\ 0& C_F\end{array}\right)+\left(\begin{array}{cc}{K}_S& -R\\ 0& K_F\end{array}\right)\right)\left\{\begin{array}{c}u\\ p\end{array}\right\}=\left\{\begin{array}{c}{f}_S\\ f_F\end{array}\right\}$$

(4)

When acoustic waves move towards the water domain, the acoustic pressure can be calculated by solving the second order partial differential equation using Equation (5). When considering that, the propagation of sound waves through a medium is linear, the shear stress is negligible, the density and compressibility of liquid mediums are constant, and the pressure is time harmonic with p = p₀e^iωt [19,23]. The HRA in the ANSYS software 19.1 formulate an equation to calculate the acoustic pressure by using the finite element method. To calculate the acoustic pressure, the water domain in (1) would be changed from the fluid domain to the acoustic domain using the Galerkin procedure principles [24] by multiplying Equation (1) with the testing function (w) and integrate over the volume to get (5) that is used to calculate {p} [24].

$$\left(-{\omega }^2[M_F]+j\omega \left[C_F\right]+\left[K_F\right]\right)\left\{p\right\}=\left\{f_F\right\}$$

(5)

Once the material properties and boundary conditions are all set, the software will solve numerically Equations (1)–(5) to get {p} in the water domain. Then, the results will be displayed in graphical colours for easier analysis. Recently, we presented the method of using the HRA to investigate the acoustic pressure to develop a new UCT design with enhanced performance [17,18,19].

2.2. Computational Fluid Dynamics (CFD)

The pattern of water flows can be found by solving a system of partial differential conservation and turbulence equations which were determined in the ANSYS Fluent software 19.1 [25]. The conservation equation of mass (6), momentum (7), and energy (8) can be described in Equations (6)–(8).

$$\frac{\partial }{\partial x_j}\left(\rho U_j\right)=0$$

(6)

$$\begin{array}{l}\frac{\partial }{\partial x_j}\left(\rho U_i{U}_j\right)=-\frac{\partial p^{\prime }}{\partial x_i}+\frac{\partial }{\partial x_j}\left[{\mu }_{eff}\left(\frac{\partial U_i}{\partial x_j}+\frac{\partial U_j}{\partial x_i}\right)\right]+S_m\\ \end{array}$$

(7)

$$\frac{\partial }{\partial x_j}\left(\rho E{U}_j\right)=\frac{\partial }{\partial x_j}\left[\mu U_j\left(\frac{\partial U_i}{\partial x_j}+\frac{\partial U_j}{\partial x_i}+\frac{2}{3}{\delta }_{ij}\frac{\partial U_i}{\partial x_j}\right)\right]$$

(8)

After considering the factors related to turbulent flow using [26] along with the researcher’s past experience using the UCT, we found that, if there was a water circulation system in the UCT, the Reynold number would be between 7500–15,000, which made the k-ε realize turbulence model suitable for the simulation. The k-ε realize turbulence model consists of two equations for turbulence kinetic energy (k) and turbulence dissipation rate (ε). As the equation’s full form, the consistent figures that were used, and the derivation of the k-ε realize are quite long and complex, readers may study further from documents [25,26].

The movement of excess particles and contaminants depends on the time which can be calculated from the particle force balance equation in the discrete phase model (DPM) [27] presented in Equation (9).

$$\frac{d{u}_p}{dt}=F_D\left(u_f-u_p\right)+\frac{g}{{\rho }_p}\left({\rho }_p-{\rho }_f\right)+F_s,$$

(9)

Since the particles are extremely small, some as small as the micron level and can change directions with the influence of fluid flow patterns, therefore F_s in (9) was considered to consist of Saffman’s lift force, virtual mass force, and the pressure gradient force. Saffman’s lift force is an external force that is important towards particle traces, must always be calculated together, and can be presented in Equation (10) [28].

$$\overrightarrow{F}=\frac{2K{\rho }_f{\nu }^{1/2}{d}_{ij}\left({\overrightarrow{u}}_f-{\overrightarrow{u}}_p\right)}{{\rho }_p{d}_p{\left(d_{lk}{d}_{kl}\right)}^{1/4}},$$

(10)

Because particles may change directions from colliding against each other or changing direction according to the flow pattern of fluids, it meant there was an interaction with continuous phases. Therefore, all behavior of the particles as mentioned can be calculated using the ANSYS Fluent 19.1 [25]. Fluent is a software used for CFD calculations based on the finite volume method principle. The model was divided into sub-elements called control volumes. The physical equations related with control volume must be conserved. Once the boundary conditions had been set, ANSYS Fluent would solve Equations (6–10) with 2 other k-ε turbulence model equations to calculate the unknown values in those elements before displaying them as numerical results. Afterwards, the unknown values were changed into colors for easier analysis. As for the definition of necessary values for the software to calculate, we shall explain that in Section 3.

3. Methodology

In this section, we discuss the research methodology used to resolve the problem and guidelines to develop the UCT for an enhanced performance. We shall discuss the first to last steps of designing a novel UCT model.

3.1. A Conventional Ultrasonic Cleaning Tank

A conventional UCT model had a capacity of 10 L. Beneath its base were 4 horn PZT4 transducers which created ultrasonic waves at a frequency of 28 kHz. Users may adjust its power between the range of 0–200 W. In Figure 2, (a) shows the CAD model and dimension of the UCT used in this research. When water was filled and the lid as well as other irrelevant parts were taken away, we were left with (b). The simplified model consisted of water which was used as the cleaning fluid. The transducers beneath had a front mass made from aluminum alloy and the back mass made from stainless steel (illustrated in Figure 1). The tank’s wall and base were made from stainless steel.

3.2. HRA Setting

The HRA was used to simulate the acoustic pressure that occurred inside the UCT in order to find the cause of why it could not clean contaminants effectively and seek a method to improve and develop the UCT. We upgraded the HRA software [22] that was used by using an extended package that was able to simulate piezoelectric [23] and acoustic materials [24] in a more accurate way. The concept of enhancing this UCT was that an appropriate design and positions of the transducers would enable the acoustic pressure to be evenly dispersed throughout the tank and be more intense. First of all, we used the UCT in Figure 2b as the prototype to create the model in Figure 3a called Model A. Apart from that, we also proposed 3 new models with designs and transducer positions that were different as illustrated in images (b–d) called models B–D, respectively. All models were set to have a capacity of 10 L, as it was the customer’s demand and also the most popular variation on the market for jewelry factories. All 4 models were then simulated to find the acoustic pressure values in the UCT using the HRA. Then the simulation results would then be compared to find the best design which has the highest area and acoustic pressure above 30,000 Pa [19]. This design was then used as the prototype to design the flow circulation system using the CFD which will be discussed in the next section. As for the mesh model used in the simulation, we created 4 mesh models, all were the hexahedral mesh type. The accuracy of solutions in hexahedral meshes is the highest. We found that after completing the mesh independent analysis, the mesh model that was most suitable for simulation had a size between 5–6 mm, which would result in a total element of between 1.6–2 million nodes, 0.4–0.5 million elements, and a maximum skewness of 0.62–0.66. Figure 4 on the left illustrates a sample of the full mesh of model A while the right one is the mesh in the cutting plane. As for the mesh of the other remaining models, although they shared some appearance similarities, the number of elements and nodes differed. These customized mesh models were reliable and suited the time and computational resources used in this research. For all the settings in every model, we used the same settings as mentioned before in [17,18,19] which were used to develop the 20 L UCT for the electronic parts factory. The material properties and other important constant values were set according to

Table 1. Material properties [17].

Domain	Type	Value
Water (45 °C)	Water density	990.15 kg/m3
	Acoustic velocity	1533.5 m/s
	Dynamic viscosity	5.7977 × 10−4 kg/m $·$ s
Aluminum alloy	Density	2770 kg/m3
	Young’s modulus	7.1 × 1010 Pa
	Poisson’s ratio	0.33
	Bulk modulus	6.9608 × 1010 Pa
	Shear modulus	2.6692 × 1010 Pa
Stainless steel	Density	7750 kg/m3
	Young’s modulus	1.93 × 1011 Pa
	Poisson’s ratio	0.31
	Bulk modulus	1.693 × 1010 Pa
	Shear modulus	7.3664 × 1010 Pa
Gold (Au)	Density	19,520 kg/m3
	Diameter	5 × 10−6 m
Chromium oxide (Cr2O3)	Density	5220 kg/m3
	Diameter	5 × 10−6 m
Lead Zirconate Titanate (PZT4)	Density	7500 kg/m3
	Permittivity constant (${\epsilon }_0$)	8.854 × 10−12 F/m
	Stiffness matrix [cE]	C11 = C22 = 1.39 × 1011, C21 = 7.78 × 1010, C31 = C32 = 7.43 × 1010, C44 = 3.06 × 1010, C55 = C66 = 2.56 × 1010 Pa
	Piezoelectric stress matrix [e]	e31- = 5.2 c/m2, e33 = 15.1 c/m2, e15 = 12.7
	Relative permittivity (${\epsilon }_r$)	K11 = 1475, K33 = 1300

. The computational resource is 18 cores of Intel Xeon 2.30 GHz with 64 GB of RAM, which required 10 min per case.

To validate the simulation results, we used the foil corrosion test. The rectangular aluminum foil with a size of 18 cm × 20 cm and 0.038 mm thick was tensely fixed using a metal structure. The foil sheets were dipped into the water at the level required in experiment using 3 min of sonication time, at a temperature of 45 °C.

At the cooperated factory, the cleaning fluid consisted of 95–97% water and surfactant mixed that caused the cavitation effect to occur faster and more intense by 3–5%. The exact ratio of this fluid is the seller’s trade secret. Still, this surfactant mixed had a density, sound velocity, and viscosity that was very similar to water and the percentage of surfactant mixed was low compared to percentage of water, therefore the authors used water as the representative of this cleaning fluid, which yielded results that were credible and practical for actual usage.

3.3. CFD Setting

CFD was used to simulate and investigate the flow to design the water circulation system and find suitable conditions, which we used ANSYS Fluent software 19.1. The concept of developing the UCT were that a suitable inlet design and cleaning condition would make the UCT’s performance better. Because of this, we divided the simulation into 2 sections to test the aforementioned concept.

In the first section, to find a suitable inlet design, we simulated the movement of particles which fell out of the product after washing with 45 °C water in a transient state. We then took the suitable model from the previous section to build 2 fluid models with different inlet shapes as in Figure 5 for (a) circular inlet and (b) rectangular inlet. There were 6 circular inlets with radius of 10 mm and 2 rectangular inlets with dimension of 35 mm × 140 mm located in the suitable positions as shown in Figure 5a,b, respectively. Both models had 2 circular outlets with radius of 10 mm located at a depth of 36.65 mm from the tank edge. The water in the pipe prior to entering inlet and outlet was designed to have a length of 3 cm to prevent it from backflowing and for faster convergence calculations [29]. We modelled that the particles that we wanted to wash were spherical in shape, were Cr₂O₃ particles, and have a radius of 5 μm. The Cr₂O₃ particles came from the product’s assembling process and can be commonly found in jewelry factories and must be eliminated. In our simulation, we modelled that the products that we wanted to wash were 8 cubes placed in the UCT center at the horizontal level that was slightly lower than the outlet. Each cube was assumed to represent a volume of 15 mm × 15 mm × 15 mm where the products were placed in the cleaning process. In simulation, the particles would be simulated by releasing them from the products’ surfaces to simulate the particle trace using DPM in a transient state as explained in 2.2. As for other necessary settings, we used the same ones that were successful in the medicine particle trace simulation in the small-volume jet nebulizer to seek the optimal design and conditions for inhaling medicine for child asthmatic patients [30].

In the second section, to find suitable conditions to use the UCT, we used the same settings as mentioned above, but simulated by using water flow rates when the inlet were 7.5, 10, and 15 L/min. We set Au and Cr₂O₃ as released particles. Au particles as the type which the jewelry factory wanted to keep for reannealing into new products.

Table 2. Cases and boundary conditions.

Case	Particle	Flow Rate (L/min)	Inlet Shape	Boundary Condition	Number of Opening	Mass Flow Rates of Water (kg/s)
1	Cr2O3	10	Circle	mass flow inlet	6	0.0278
				mass flow outlet	2	0.0833
2			Rectangle	mass flow inlet	2	0.0833
				mass flow outlet	2	0.0833
3		15		mass flow inlet	2	0.1250
				mass flow outlet	2	0.1250
4		7.5		mass flow inlet	2	0.0625
				mass flow outlet	2	0.0625
5	Au	7.5		mass flow inlet	2	0.0625
				mass flow outlet	2	0.0625
6		10		mass flow inlet	2	0.0833
				mass flow outlet	2	0.0833
7		15		mass flow inlet	2	0.1250
				mass flow outlet	2	0.1250

shows the cases and boundary conditions in the CFD simulation which consisted of 7 cases. For calculations in the transient state, we used 12,000 timesteps, 5 ms per 1 timestep, 20 iterations per 1 timestep, and 10⁻⁴ convergence criteria. Therefore, the computer must calculate a total of 12,000 points with 240,000 iterations, ensuring that the settings we used were detailed enough to yield accurate simulation results. When the simulation was complete, the result showed the particle trace at every 5 ms, starting from 0s to 60s of the cleaning time. When we count the number of particles that were eliminated through the outlet depending on time for analysis, we were able to find the proper inlet design and condition to design a novel UCT model. The computational time was 10 h per case.

4. Results

4.1. Validation and HRA Approach

In order to check the correctness of the simulated acoustic pressure, Figure 6 shows the acoustic pressure distribution results compared to the results from foil corrosion test for a water temperature of 45 °C using model A. As the results were symmetric, we therefore showed the compared results, half a plane each. The small picture below shows the plane’s position that was used in the comparison. Notice that both the results were highly consistent to one another. For the position in the marker, although the foil may appear to be intact, it actually had small holes scattered through the entire piece, meaning that if the cleaning time was longer, these holes would become larger, eventually tearing the foil. Figure 6a shows the simulation and test results when placed at a height of 5.5 cm in vertical plane from the bottom of the UCT. We learned that this height was the beginning height which contributed to effective cleaning, which was also reported in [31] that the first suitable cleaning position was at 1 wavelength. In this research, the UCT had a frequency (f) of 28 kHz and a submerged acoustic wave speed (v) of 1533.5 m/s. From the equation v = fλ, 1 wavelength (λ) was approximately 5.5 cm, as found in Figure 6a. If the distance between the cleaning object and UTC’s base was shorter than this, the cleaning process would not occur, or would occur though unsuccessful as the acoustic pressure was not high enough to make the cavitation intense enough to clean objects. As the acoustic pressure distribution is consistent with the positions where the foil was corroded and the report the study [17,18,19,32], therefore, the simulation results were deemed as reliable and could be used to accurately predict the cleaning positions.

To further enhance this UCT for even higher performance, we used the HRA to simulate the acoustic pressure of every model in Figure 3. Figure 7 shows the acoustic pressure distribution in the same vertical plane with Figure 6a. We found that the newly designed models B–D had higher acoustic pressure than model A. The acoustic pressure distributions of all models were simulated and discovered to be similar as the transducer’s position only changed slightly. Models B and D had the highest possibility to be further developed in the future as they resulted in an acoustic pressure higher than other models and also was powerful at the center, the position where products were washed. Figure 8 shows the acoustic pressure distribution at a horizontal level at a depth of 5 cm from the water surface, the same level where products were washed for models in Figure 3a–d, accordingly. The red color is the region where the acoustic pressure is higher than 30 kPa, which is the cleaning area that makes the cavitation strong enough for cleaning 10–150 micrometer particles [19]. When we compared the sizes of the cleaning area, model D had the largest cleaning area of 100.83 cm², which increased up to 39.65% compared to model A which cleaning area was 72.20 cm², and larger than model B as well. From Figure 7 and Figure 8, the acoustic pressure distribution indicated that the design of the UCT and transducer position did affect acoustic pressure distribution and cleaning area, consistent to the report in [14,15,16,17,18,19]. Actually, if we relocated some transducers to the side as in the study [17,18,19], we would get a larger cleaning area and higher acoustic pressure than in this study. Still, this change would make the UCT design larger and would require a change in the electronic circuit, resulting in higher production costs which will not be convenient to actual practices and difficult for maintenance thus will not meet the demands of the jewelry factories. Therefore, model D was the most appropriate to be further developed.

4.2. CFD Approach

To find a suitable inlet shape, we used model D as the prototype to create a fluid model as in Figure 5 and simulated the particle trace using ANSYS Fluent software on the conditions in Table 2. Figure 9 shows the simulation results of 36,800 Cr₂O₃ particle traces during 10–60 s for (a) case 1, circular inlet and (b) case 2, rectangular inlet. We noticed that in both cases, when the time reached 10s, the particles started detaching from the product’s surface and floated along the flow. As time passed, this flow removed the particles out from the UCT through the outlet more and more. At 60s, there were not any particles floating outside the streamline, so as time passed, these particles increased in quantity and may be the cause of recontamination. In the conventional UCT model, as there was not a circulation flow, in the beginning it was able to clean products effectively as there was only a small amount of particles remaining in the UCT, however, after many cleaning sessions, these particles would increase in quantity as it is not removed from the UCT, causing recontamination. This is the reason why the conventional UCT noticed by customers could not clean products effectively. For an even more detailed analysis, we simulated cases 1 and 2 again by emitting 147,200 Cr₂O₃ particles for our computer to record accumulated particles that were eliminated out of the UCT through the outlet. Results of this simulation are shown in Figure 10. The 147,200 number is the maximum value that can be used for emitting the particles by the software and mesh model settings. We also simulated using 36,800 and 73,600 particles; however, the conclusion remained the same. During 0–10 s the particles would start to detach from the product surfaces but would not float to reach the outlet yet. During 10–25 s more particles would be eliminated. In both cases the rate was similar. After 25 s onwards, case 2′s circulation system would eliminate more particles than case 1 and throughout the remaining cleaning time. After the completion of 60 s, 33,936 particles still remained in case 2 while 59,192 particles still remained in case 1. Thus, case 2 could eliminate 25,256 more particles compared to case 1, or a percentage of 17.16% of all the particles. Therefore, it could be summarized that the circulation system in case 2 was more effective than case 1 and could remove 17.16% more particles. The animation files to support our discussion of Figure 9 and Figure 10 are Cir_Inlet.mp4 and Rec_Inlet.mp4 in the Supplementary Materials.

In order to find the reason that made case 2 better than case 1, Figure 11 shows the circulation system’s streamline within the UCT from a side view for (a) case 1 and (b) case 2. In both cases, the water would flow into the inlet and flow directly upwards until it collided with the product and exited through the outlet. That meant that in this circulation system, not only did it send cavitation bubbles directly to the product for better cleaning, but it also helped send unwanted or excess particles away through the outlet as well (See Figure 9). From Figure 11a, notice where the red arrow points have many streamlines released from many inlets, making the turbulent flow and disorderly. This turbulence caused particles to float around and remain within the UCT without being eliminated, leading to recontamination. Contrastingly, the same positions in Figure 11b were more orderly and had predictable streamlines. The animation files to support the discussion of Figure 11 are Cir_Streamline.mp4 and Rec_Streamline.mp4 in the Supplementary Materials. We also simulated case 1 by using 1 and 2 circular inlets with the same boundary condition, but the simulated results did not alter the conclusion. In Figure 5a,b, since the total cross-section areas were 1.88 × 10⁻³ m² for circular inlets and 2.24 × 10⁻³ m² for rectangular inlets, having a suitable shape, large cross-section area, and proper shape of inlet would prevent turbulence from occurring. Therefore, the design of the inlet and outlet’s shape were crucial towards the UCT design. This helped us confirm that rectangular inlets designed in Figure 5b made water circulation systems more effective than circular inlets.

To find the optimal condition for cleaning, we simulated cases 3–7 in Table 2 using the same method as in Figure 10. Simulation results are shown in Figure 12.

Table 3. Simulation results of total accumulated particles.

Flow Rate (L/min)	Particle	Total Number of Particles Eliminated at 60 s	Efficiency of Cleaning
7.5	Cr2O3 Au	97,328 95,368	66.12% 64.79%
10	Cr2O3 Au	113,264 107,964	76.95% 73.35%
15	Cr2O3 Au	124,188 117,972	84.37% 80.14%

shows the total accumulated particles that were eliminated within 60 s. From Figure 12 and Table 3, we found that the higher the flow rate, the more particles were eliminated. In every flow rate, the circulation system was able to eliminate more Cr₂O₃ particles than Au, as Cr₂O₃ particles are lighter in weight compared to Au, thus enabling them to float out of the UCT easier. From the condition in Table 2, the particle elimination effectiveness was between 66.12–84.37% compared to the conventional UTC without a water circulation system which all particles would remain floating in the UCT. All these results were from a simulation of 60 s, but in the actual factory, the cleaning process took at least 180 s, so the actual cleaning effectiveness should be higher than our findings. The results here could confirm that a flow rate between 7.5–15 L/min was the best condition to enable the water circulation flow to eliminate remaining particles from the UCT effectively. The results of this report were consistent with using air circulation flow in [33,34,35] as it prevented and removed contaminant particles in the machines and clean rooms at a hard disk drive factory. Using a flow rate that is too low can eliminate particles for a period that’s too long, but using a flow rate that is too high may make the UCT unable to clean products thoroughly as explained in the next paragraph.

The model that we presented had only two outlets. We also simulated changing the shape and size of the outlet and learned that the larger the outlet (with many routes and high flow rates), the more particles were eliminated from the UTC. However, details of those results were not included in this article as the contents were too long. The obtained results were consistent with a report from the manufacturer, that in the case when customers would like a UCT with a water circulation system, the manufacturer would generally design an UCT that only overflows at the brim at a high flow rate, as they believed this to be the most effective cleaning method. However, we were convinced that this belief would only make the cavitation bubbles flow out of the tank quickly and lessen the rate a bubble collapses, decreasing the cleaning effectiveness as mentioned in the report [13]. Apart from that, the overflowing UCT also required a powerful pump that is noisy, difficult to move, and has high maintenance costs as well. In actual UCTs with a water circulation system that is commercially manufactured, it has a bucket on the outside to store the solutions of heavy metals from cleaning products. When Au, Cr₂O₃, and other metal particles are eliminated from the UCT, it will be stored in that bucket. Once the bucket is full, it will go through a chemical process to separate the valuable metals such as Au, Pt, Ag, and etc. out for recycling. As for the nonvaluable metals, they will remain in that solution, be treated and returned back into nature. The circular system that was designed in this study also supports this metal separating process to be even more effective. All results from this study were given to the manufacturer to apply, with excellent feedback. They applied the knowledge from this research to develop and manufacture new and enhanced UCTs for commercial purposes that meet the requirements of customers.

Presently, the most popular ultrasonic wave cleaning device used in large industrial factories are the multi frequency type, as it is able to wash many sizes of contaminants in one cycle and can be used to clean products with complex designs unlike other general washing processes. However, the HRA can only be used to design single frequency UCTs, thus seeking new methods to design multi frequency UCTs shall be a challenge for the researchers to continue studying and learning.

5. Conclusions

The 10 L UCT with four horn transducers was made by a manufacturer who received feedback from a customer who operated a jewelry factory that the UCT was not cleaning products effectively. To resolve that problem, we used the HRA and CFD to find the cause to the problem and developed a new UTC with enhanced performance. Using the actual conditions from the customer, HRA results showed that the conventional UCT had low acoustic pressure and a cleaning area that was too small, becoming the reason why it could not clean products effectively. The results were consistent with the foil corrosion test, assuring us that the simulation was credible. To resolve the problem and develop an improved model of the UCT, we designed three novel UCT models with different sizes and transducer positions from the conventional UCT. The HRA and CFD were applied to find the optimal model of UTC and conditions for cleaning. Results of the HRA enabled us to design a new tank with 39.65% higher cleaning effectiveness, as this had a higher acoustic pressure in the center of the UCT and a larger cleaning area. We developed this model further by adding a water circulation system and simulate the cleaning process using the CFD for a duration of 60 s. We learned that using a rectangular inlet enabled the water circulation system to eliminate particles 17.16% better than the circular inlet, because the rectangular inlet causes the streamline to be more orderly. When we used this model with a rectangular inlet to simulate the cleaning process to find the best condition using flow rates of 7.5 L/min, 10 L/min, and 15 L/min, we found that the effectiveness of eliminating Au and Cr₂O₃ particles were between the range of 64.79–84.37%, was better than the conventional UCT. The results from this research received excellent feedback from the manufacturer. We could confirm that the HRA and CFD were suitable methods that solved the problem and helped develop a UCT with enhanced performance as demanded by the customer.