Shear Bands Topology in the Deformed Bulk Metallic Glasses
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Measurement of the Long-Range Stress Fields Produced by Shear Bands
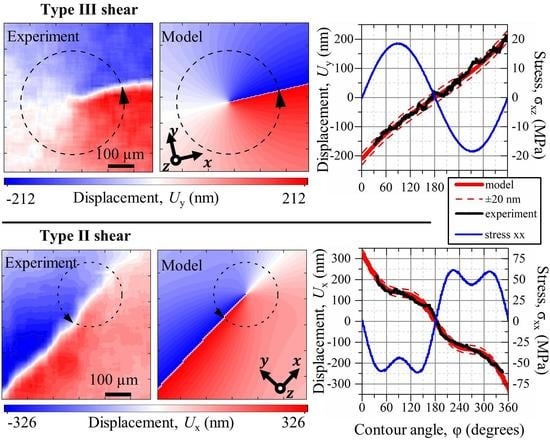
3.2. Mode II Shear Morphology
3.3. Mode III Shear Morphology
3.4. Shear Offset Fluctuations
3.5. Shear Bands’ Behaviour during Indentation
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgements
Conflicts of Interest
References
- Demetriou, M.D.; Launey, M.E.; Garrett, G.; Schramm, J.P.; Hofmann, D.C.; Johnson, W.L.; Ritchie, R.O. A damage-tolerant glass. Nat. Mater. 2011, 10, 123–129. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.Q.; Zhang, Z.F. Strengthening and toughening metallic glasses: The elastic perspectives and opportunities. J. Appl. Phys. 2014, 115, 163505. [Google Scholar] [CrossRef]
- Schroers, J.; Kumar, G.; Hodges, T.M.; Chan, S.; Kyriakides, T.R. Bulk metallic glasses for biomedical applications. JOM 2009, 61, 21–29. [Google Scholar] [CrossRef]
- Trexler, M.M.; Thadhani, N.N. Mechanical properties of bulk metallic glasses. Prog. Mater. Sci. 2010, 55, 759–839. [Google Scholar] [CrossRef]
- Greer, A.L.; Cheng, Y.Q.; Ma, E. Shear bands in metallic glasses. Mater. Sci. Eng. R 2013, 74, 71–132. [Google Scholar] [CrossRef]
- Zhang, Y.; Greer, A.L. Thickness of shear bands in metallic glasses. Appl. Phys. Lett. 2006, 89, 071907. [Google Scholar] [CrossRef]
- Park, E.S. Understanding of the Shear Bands in Amorphous Metals. Appl. Microsc. 2015, 45, 63–73. [Google Scholar] [CrossRef]
- Maaß, R.; Birckigt, P.; Borchers, C.; Samwer, K.; Volkert, C.A. Long range stress fields and cavitation along a shear band in a metallic glass: The local origin of fracture. Acta Mater. 2015, 98, 94–102. [Google Scholar] [CrossRef]
- Qu, R.T.; Wu, F.; Zhang, Z.-F.; Eckert, J. Direct observations on the evolution of shear bands into cracks in metallic glass. J. Mater. Res. 2009, 24, 3130–3135. [Google Scholar] [CrossRef]
- Qu, R.T.; Wang, S.G.; Wang, X.D.; Liu, Z.Q.; Zhang, Z.F. Revealing the shear band cracking mechanism in metallic glass by X-ray tomography. Scr. Mater. 2017, 133, 24–28. [Google Scholar] [CrossRef]
- Das, J.; Tang, M.B.; Kim, K.B.; Theissmann, R.; Baier, F.; Wang, W.; Eckert, J. “Work-Hardenable” ductile bulk metallic glass. Phys. Rev. Lett. 2005, 94, 205501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Z.T.; Pan, J.; Li, Y.; Schuh, C.A. Densification and strain hardening of a metallic glass under tension at room temperature. Phys. Rev. Lett. 2013, 111, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Takayama, S. Work-hardening and susceptibility to plastic flow in metallic glasses (rolling deformation). J. Mater. Sci. 1981, 16, 2411–2418. [Google Scholar] [CrossRef]
- Wang, Y.; Li, M.; Xu, J. Toughen and harden metallic glass through designing statistical heterogeneity. Scr. Mater. 2016, 113, 10–13. [Google Scholar] [CrossRef]
- Ross, P.; Küchemann, S.; Derlet, P.M.; Yu, H.B.; Arnold, W.; Liaw, P.; Samwer, K.; Maaß, R. Linking macroscopic rejuvenation to nano-elastic fluctuations in a metallic glass. Acta Mater. 2017, 138, 111–118. [Google Scholar] [CrossRef]
- Hassani, M.; Lagogianni, A.E.; Varnik, F. Probing the degree of heterogeneity within a shear band of a model glass. Phys. Rev. Lett. 2019, 123, 195502. [Google Scholar] [CrossRef] [Green Version]
- Binkowski, I.; Schlottbom, S.; Leuthold, J.; Ostendorp, S.; Divinski, S.V.; Wilde, G. Sub-micron strain analysis of local stick-slip motion of individual shear bands in a bulk metallic glass. Appl. Phys. Lett. 2015, 107, 221909. [Google Scholar] [CrossRef] [Green Version]
- Rösner, H.; Peterlechner, M.; Kübel, C.; Schmidt, V.; Wilde, G. Density changes in shear bands of a metallic glass determined by correlative analytical transmission electron microscopy. Ultramicroscopy 2014, 142, 1–9. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, G.; Estévez, D.; Chang, C.; Wang, X. Evolution of shear bands into cracks in metallic glasses. J. Alloys Compd. 2015, 621, 238–243. [Google Scholar] [CrossRef]
- Hufnagel, T.C.; Schuh, C.A.; Falk, M.L. Deformation of metallic glasses: Recent developments in theory, simulations, and experiments. Acta Mater. 2016, 109, 375–393. [Google Scholar] [CrossRef] [Green Version]
- Dahmen, K.A.; Ben-Zion, Y.; Uhl, J.T. A simple analytic theory for the statistics of avalanches in sheared granular materials. Nat. Phys. 2011, 7, 554–557. [Google Scholar] [CrossRef] [Green Version]
- Takeuchi, S.; Edagawa, K. Atomistic simulation and modeling of localized shear deformation in metallic glasses. Prog. Mater. Sci. 2011, 56, 785–816. [Google Scholar] [CrossRef]
- Shi, L.T. Dislocation-like defects in an amorphous Lennard-Jones solid. Mater. Sci. Eng. 1986, 81, 509–514. [Google Scholar] [CrossRef]
- Spaepen, F. A microscopic mechanism for steady state inhomogeneous flow in metallic glasses. Acta Metall. 1976, 25, 407–415. [Google Scholar] [CrossRef]
- Shrivastav, G.P.; Chaudhuri, P.; Horbach, J. Yielding of glass under shear: A directed percolation transition precedes shear-band formation. Phys. Rev. E 2016, 94, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Vinogradov, A.; Seleznev, M.; Yasnikov, I.S. Dislocation characteristics of shear bands in metallic glasses. Scr. Mater. 2017, 130, 138–142. [Google Scholar] [CrossRef]
- Qu, R.T.; Liu, Z.Q.; Wang, G.; Zhang, Z.F. Progressive shear band propagation in metallic glasses under compression. Acta Mater. 2015, 91, 19–33. [Google Scholar] [CrossRef]
- Xu, Y.; Shi, B.; Ma, Z.; Li, J. Evolution of shear bands, free volume, and structure in room temperature rolled Pd40Ni40P20 bulk metallic glass. Mater. Sci. Eng. A 2015, 623, 145–152. [Google Scholar] [CrossRef]
- Huo, L.S.; Wang, J.Q.; Huo, J.T.; Zhao, Y.Y.; Men, H.; Chang, C.T.; Wang, X.M.; Li, R.W. Interactions of Shear Bands in a Ductile Metallic Glass. J. Iron Steel Res. Int. 2016, 23, 48–52. [Google Scholar] [CrossRef]
- Kovács, Z.; Schafler, E.; Szommer, P.; Révész, Á. Localization of plastic deformation along shear bands in Vitreloy bulk metallic glass during high pressure torsion. J. Alloys Compd. 2014, 593, 207–212. [Google Scholar] [CrossRef]
- Bouzakher, B.; Benameur, T.; Yavari, A.R.; Sidhom, H. In situ characterization of a crack trajectory and shear bands interaction in metallic glasses. J. Alloys Compd. 2007, 434–435, 52–55. [Google Scholar] [CrossRef]
- Haag, F.; Beitelschmidt, D.; Eckert, J.; Durst, K. Influences of residual stresses on the serrated flow in bulk metallic glass under elastostatic four-point bending—A nanoindentation and atomic force microscopy study. Acta Mater. 2014, 70, 188–197. [Google Scholar] [CrossRef]
- Merson, E.; Danilov, V.; Merson, D.; Vinogradov, A. Confocal laser scanning microscopy: The technique for quantitative fractographic analysis. Eng. Fract. Mech. 2017, 183, 147–158. [Google Scholar] [CrossRef]
- Huang, H.; Yan, J. Investigating shear band interaction in metallic glasses by adjacent nanoindentation. Mater. Sci. Eng. A 2017, 704, 375–385. [Google Scholar] [CrossRef]
- Nollmann, N.; Binkowski, I.; Schmidt, V.; Rösner, H.; Wilde, G. Impact of micro-alloying on the plasticity of Pd-based Bulk Metallic Glasses. Scr. Mater. 2015, 111, 119–122. [Google Scholar] [CrossRef] [Green Version]
- Li, H.F.; Zheng, Y.F.; Xu, F.; Jiang, J.Z. In vitro investigation of novel Ni free Zr-based bulk metallic glasses as potential biomaterials. Mater. Lett. 2012, 75, 74–76. [Google Scholar] [CrossRef]
- Vinogradov, A.; Danyuk, A.; Khonik, V.A. Localized and homogeneous plastic flow in bulk glassy Pd40Cu30Ni10P20: An acoustic emission study. J. Appl. Phys. 2013, 113, 153503. [Google Scholar] [CrossRef]
- Seleznev, M.; Vinogradov, A. Note: High-speed optical imaging powered by acoustic emission triggering. Rev. Sci. Instrum. 2014, 85, 076103. [Google Scholar] [CrossRef]
- Hirth, J.P.; Lothe, J. Theory of Dislocations, 2nd ed.; Wiley: New York, NY, USA, 1982. [Google Scholar]
- Volterra, V. On the equilibrum of multiply-connected elastic bodies. Ann. Sci. Éc. Norm. Supér.. 1907, 24, 401–517. [Google Scholar] [CrossRef] [Green Version]
- Zolotukhin, I.V.; Belyavskii, V.I.; Khonik, V.A.; Ryabtseva, T.N. Internal friction in cold-rolled metallic glasses Cu50Ti50 and Ni78Si8B14. Phys. Status Solidi Appl. Res. 1989, 116, 255–265. [Google Scholar] [CrossRef]
- Khonik, V.A.; Spivak, L.V. On the nature of low temperature internal friction peaks in metallic glasses. Acta Mater. 1996, 44, 367–381. [Google Scholar] [CrossRef]
- Khonik, V.A. Dislocation-like relaxations in cold deformed metallic glasses. J. Alloys Compd. 1994, 211–212, 114–117. [Google Scholar] [CrossRef]
- Liu, C.; Roddatis, V.; Kenesei, P.; Maaß, R. Shear-band thickness and shear-band cavities in a Zr-based metallic glass. Acta Mater. 2017, 140, 206–216. [Google Scholar] [CrossRef]
- Clouet, E.; Ventelon, L.; Willaime, F. Dislocation core energies and core fields from first principles. Phys. Rev. Lett. 2009, 102, 055502. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.H.; Wang, G.; Pan, M.X.; Yu, P.; Zhao, D.Q.; Wang, W.H. Deformation behaviors and mechanism of Ni-Co-Nb-Ta bulk metallic glasses with high strength and plasticity. J. Mater. Res. 2007, 22, 869–875. [Google Scholar] [CrossRef]
- Laureys, A.; Depover, T.; Petrov, R.; Verbeken, K. Influence of sample geometry and microstructure on the hydrogen induced cracking characteristics under uniaxial load. Mater. Sci. Eng. A 2017, 690, 88–95. [Google Scholar] [CrossRef]
- Wang, X.D.; Qu, R.T.; Liu, Z.Q.; Zhang, Z.F. Evolution of shear-band cracking in metallic glass under cyclic compression. Mater. Sci. Eng. A 2017, 696, 267–272. [Google Scholar] [CrossRef]
- Gilman, J.J. Flow via dislocations in ideal glasses. J. Appl. Phys. 1973, 44, 675–679. [Google Scholar] [CrossRef]
- Xie, S.; George, E.P. Hardness and shear band evolution in bulk metallic glasses after plastic deformation and annealing. Acta Mater. 2008, 56, 5202–5213. [Google Scholar] [CrossRef]





© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seleznev, M.; Vinogradov, A. Shear Bands Topology in the Deformed Bulk Metallic Glasses. Metals 2020, 10, 374. https://doi.org/10.3390/met10030374
Seleznev M, Vinogradov A. Shear Bands Topology in the Deformed Bulk Metallic Glasses. Metals. 2020; 10(3):374. https://doi.org/10.3390/met10030374
Chicago/Turabian StyleSeleznev, Mikhail, and Alexei Vinogradov. 2020. "Shear Bands Topology in the Deformed Bulk Metallic Glasses" Metals 10, no. 3: 374. https://doi.org/10.3390/met10030374
APA StyleSeleznev, M., & Vinogradov, A. (2020). Shear Bands Topology in the Deformed Bulk Metallic Glasses. Metals, 10(3), 374. https://doi.org/10.3390/met10030374