Effect of Annealing on Strain Rate Sensitivity of Metallic Glass under Nanoindentation
Abstract
:1. Introduction
2. Materials and Methods
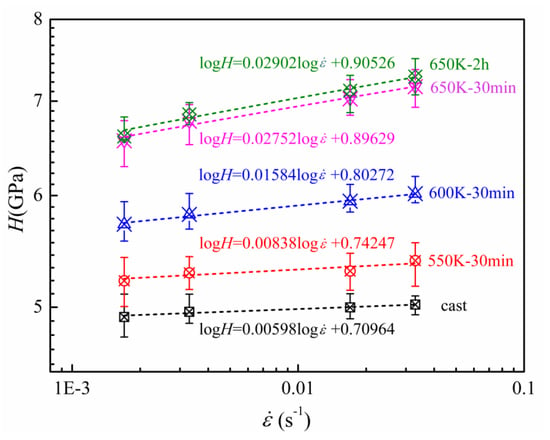
3. Results
4. Discussion
5. Conclusions
Funding
Conflicts of Interest
References
- Wang, Y.W.; Bian, X.L.; Wu, S.W.; Hussain, I.; Jia, Y.D.; Yi, J.; Wang, G. Rate dependent of strength in metallic glasses at different temperatures. Sci. Rep. 2016, 6, 27747. [Google Scholar] [CrossRef] [Green Version]
- Tönnies, D.; Samwer, K.; Derlet, P.M.; Volkert, C.A.; Maaß, R. Rate-dependent shear-band initiation in a metallic glass. Appl. Phys. Lett. 2015, 106, 171907–171910. [Google Scholar] [CrossRef]
- Burgess, T.; Laws, K.J.; Ferry, M. Effect of loading rate on the serrated flow of a bulk metallic glass during nanoindentation. Acta Mater. 2008, 56, 4829–4835. [Google Scholar] [CrossRef]
- Schuh, C.A.; Nieh, T.G. A nanoindentation study of serrated flow in bulk metallic glasses. Acta Mater. 2003, 51, 87–99. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Singh, G.; Prasad, K.E.; Narasimhan, R.; Ramamurty, U. On the strain rate sensitivity of plastic flow in metallic glasses. Mater. Sci. Eng. A 2015, 625, 245–251. [Google Scholar] [CrossRef]
- Shi, Y.; Falk, M.L. Stress-induced structural transformation and shear banding during simulated nanoindentation of a metallic glass. Acta Mater. 2007, 55, 4317–4324. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, Y.J.; Dai, L.H. Understanding the serrated flow and Johari-Goldstein relaxation of metallic glasses. J. Non Cryst. Solids. 2016, 444, 23–30. [Google Scholar] [CrossRef] [Green Version]
- Liao, G.; Long, Z.; Zhao, M.; Zhong, M.; Liu, W.; Chai, W. Serrated flow behavior in a Pd-based bulk metallic glass under nanoindentation. J. Non Cryst. Solids. 2017, 460, 47–53. [Google Scholar] [CrossRef]
- Jiang, S.Y.; Jiang, M.Q.; Dai, L.H.; Yao, Y.G. Atomistic origin of rate-dependent serrated plastic flow in metallic glasses. Nanoscale Res. Lett. 2008, 3, 524–529. [Google Scholar] [CrossRef] [Green Version]
- Jiang, W.H.; Fan, G.J.; Liu, F.X.; Wang, G.Y.; Choo, H.; Liaw, P.K. Spatiotemporally inhomogeneous plastic flow of a bulk-metallic glass. Int. J. Plast. 2008, 24, 1–16. [Google Scholar] [CrossRef]
- Harmon, J.S.; Demetriou, M.D.; Johnson, W.L.; Samwer, K. Anelastic to plastic transition in metallic glass-forming liquids. Phys. Rev. Lett. 2007, 99, 135502–135505. [Google Scholar] [CrossRef] [Green Version]
- Li, M.C.; Jiang, M.Q.; Yang, S.; Jiang, F.; He, L.; Sun, J. Effect of strain rate on yielding strength of a Zr-based bulk metallic glass. Mater. Sci. Eng. A 2017, 680, 21–26. [Google Scholar] [CrossRef] [Green Version]
- Shimizu, F.; Ogata, S.; Li, J. Yield point of metallic glass. Acta Mater. 2006, 54, 4293–4298. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Yang, Y.; Liu, C.T. Yielding and shear banding of metallic glasses. Acta Mater. 2013, 61, 5928–5936. [Google Scholar] [CrossRef]
- Yang, B.; Nieh, T.G. Effect of the nanoindentation rate on the shear band formation in an Au-based bulk metallic glass. Acta Mater. 2007, 55, 295–300. [Google Scholar] [CrossRef]
- Greer, A.L.; Cheng, Y.Q.; Ma, E. Shear bands in metallic glasses. Mater. Sci. Eng. R 2013, 74, 71–132. [Google Scholar] [CrossRef]
- Li, L.; Homer, E.R.; Schuh, C.A. Shear transformation zone dynamics model for metallic glasses incorporating free volume as a state variable. Acta Mater. 2013, 61, 3347–3359. [Google Scholar] [CrossRef] [Green Version]
- Jiang, M.Q.; Wilde, G.; Dai, L.H. Shear band dilatation in amorphous alloys. Scr. Mater. 2017, 127, 54–57. [Google Scholar] [CrossRef] [Green Version]
- Zhao, P.Y.; Li, J.; Hwang, J.; Wang, Y.Z. Influence of nanoscale structural heterogeneity on shear banding in metallic glasses. Acta Mater. 2017, 134, 104–115. [Google Scholar] [CrossRef]
- Murali, P.; Ramamurty, U. Embrittlement of a bulk metallic glass due to sub-Tg annealing. Acta Mater. 2005, 53, 1467–1478. [Google Scholar] [CrossRef]
- Jiang, F.; Jiang, M.Q.; Wang, H.F.; Zhao, Y.L.; He, L.; Sun, J. Shear transformation zone volume determining ductile–brittle transition of bulk metallic glasses. Acta Mater. 2011, 59, 2057–2068. [Google Scholar] [CrossRef]
- Xue, F.; Wang, F.; Huang, P.; Lu, T.J.; Xu, K.W. Structural inhomogeneity and strain rate dependent indentation size effect in Zr-based metallic glass. Mater. Sci. Eng. A 2016, 655, 373–378. [Google Scholar] [CrossRef]
- Zhou, Q.; Du, Y.; Han, W.C.; Ren, Y.; Zhai, H.M.; Wang, H.F. Identifying the origin of strain rate sensitivity in a high entropy bulk metallic glass. Scr. Mater. 2019, 164, 121–125. [Google Scholar] [CrossRef]
- Pan, D.; Yokoyama, Y.; Fujita, T.; Liu, Y.H.; Kohara, S.; Inoue, A.; Chen, M.W. Correlation between structural relaxation and shear transformation zone volume of a bulk metallic glass. Appl. Phys. Lett. 2009, 95, 141909. [Google Scholar] [CrossRef]
- Chu, Q.; Xu, S.; Zhu, X.; Zhu, Z.; Zhang, H.; Bai, R.; Lei, Z.; Yan, C. Effects of testing conditions on the deformation behaviour of a Ti-based bulk metallic glass. Mater. Sci. Eng. A 2019, 766, 138404. [Google Scholar] [CrossRef]
- Cheng, L.; Jiao, Z.M.; Ma, S.G.; Qiao, J.W.; Wang, Z.H. Serrated flow behaviors of a Zr-based bulk metallic glass by nanoindentation. J. Appl. Phys. 2014, 115, 084907. [Google Scholar] [CrossRef]
- Ma, Y.; Ye, J.H.; Peng, G.J.; Wen, D.H.; Zhang, T.H. Nanoindentation study of size effect on shear transformation zone size in a Ni–Nb metallic glass. Mater. Sci. Eng. A 2015, 627, 153–160. [Google Scholar] [CrossRef]
- Chen, Z.Q.; Huang, L.; Huang, P.; Xu, K.W.; Wang, F.; Lu, T.J. Clarification on shear transformation zone size and its correlation with plasticity for Zr-based bulk metallic glass in different structural states. Mater. Sci. Eng. A 2016, 677, 349–355. [Google Scholar] [CrossRef]
- Li, M.C.; Jiang, M.Q.; Jiang, F.; He, L.; Sun, J. Testing effects on hardness of a Zr-based metallic glass under nanoindentation. Scr. Mater. 2017, 138, 120–123. [Google Scholar] [CrossRef] [Green Version]
- Pan, D.; Inoue, A.; Sakurai, T.; Chen, M.W. Experimental characterization of shear transformation zones for plastic flow of bulk metallic glasses. Proc. Natl Acad. Sci. USA 2008, 105, 14769–14772. [Google Scholar] [CrossRef] [Green Version]
- Evenson, Z.; Busch, R. Equilibrium viscosity, enthalpy recovery and free volume relaxation in a Zr44Ti11Ni10Cu10Be25 bulk metallic glass. Acta Mater. 2011, 59, 4404–4415. [Google Scholar] [CrossRef]
- Li, M.C.; Jiang, M.Q.; Li, G.; He, L.; Sun, J.; Jiang, F. Ductile to brittle transition of fracture of a Zr-based bulk metallic glass: Strain rate effect. Intermetallics 2016, 77, 34–40. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Jang, J.-I.; Yoo, B.-G.; Kim, Y.-J.; Oh, J.-H.; Choi, I.-C.; Bei, H. Indentation size effect in bulk metallic glass. Scr. Mater. 2011, 64, 753–756. [Google Scholar] [CrossRef]
- Ye, J.C.; Lu, J.; Liu, C.T.; Wang, Q.; Yang, Y. Atomistic free-volume zones and inelastic deformation of metallic glasses. Nat. Mater. 2010, 9, 619–623. [Google Scholar] [CrossRef]
- Lu, Z.; Yang, X.N.; Sun, B.A.; Li, Y.Z.; Chen, K.; Wang, W.H.; Bai, H.Y. Divergent strain acceleration effects in metallic glasses. Scr. Mater. 2017, 130, 229–233. [Google Scholar] [CrossRef]
- Şopu, D.; Scudino, S.; Bian, X.L.; Gammer, C.; Eckert, J. Atomic-scale origin of shear band multiplication in heterogeneous metallic glasses. Scr. Mater. 2020, 178, 57–61. [Google Scholar] [CrossRef]
- Wang, C.; Cao, Q.P.; Wang, X.D.; Zhang, D.X.; Ramamurty, U.; Narayan, R.L.; Jiang, J. Intermediate Temperature Brittleness in Metallic Glasses. Adv. Mater. 2017, 29, 1605537–1605542. [Google Scholar] [CrossRef]
- Li, M.C.; Jiang, M.Q.; Ding, G.; Peng, Z.H.; Jiang, F.; He, L.; Sun, J. The correlation between weakest configurations and yield strength of Zr-based metallic glasses. J. Non Cryst. Solids 2017, 468, 52–57. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Ye, Y.F.; Sun, B.A.; Liu, C.T.; Shi, S.Q.; Yang, Y. Softening-induced plastic flow instability and indentation size effect in metallic glass. J. Mehc. Phys. Solids 2015, 77, 70–85. [Google Scholar] [CrossRef]
- Jiang, M.Q.; Wilde, G.; Dai, L.H. Origin of stress overshoot in amorphous solids. Mech. Mater. 2015, 81, 72–83. [Google Scholar] [CrossRef]
- Heggen, M.; Spaepen, F.; Feuerbacher, M. Creation and annihilation of free volume during homogeneous flow of a metallic glass. J. Appl. Phys. 2005, 97, 033506. [Google Scholar] [CrossRef] [Green Version]
- De Hey, P.; Sietsma, J.; Van Den Beukel, A. Structural disordering in amorphous Pd40Ni40P20 induced by high temperature deformation. Acta Mater. 1998, 46, 5873–5882. [Google Scholar] [CrossRef]
- Spaepen, F. A microscopic mechanism for steady state inhomogeneous flow in metallic glasses. Acta Metall. 1977, 25, 407–415. [Google Scholar] [CrossRef]
- Qu, D.D.; Liss, K.D.; Sun, Y.J.; Reid, M.; Almer, J.D.; Yan, K.; Wang, Y.B.; Liao, X.Z.; Shen, J. Structural origins for the high plasticity of a Zr–Cu–Ni–Al bulk metallic glass. Acta Mater. 2012, 61, 321–330. [Google Scholar] [CrossRef]
- Chen, L.Y.; Fu, Z.D.; Zhang, G.Q.; Hao, X.P.; Jiang, Q.K.; Wang, X.D.; Cao, Q.P.; Franz, H.; Liu, Y.G.; Xie, H.S.; et al. New Class of Plastic Bulk Metallic Glass. Phys. Rev. Lett. 2008, 100, 075501. [Google Scholar] [CrossRef] [PubMed]
- Kawamura, Y.; Shibata, T.; Inoue, A.; Masumoto, T. Stress overshoot in stress-strain curves of Zr65Al10Ni10Cu15 metallic glass. Appl. Phys. Lett. 1997, 71, 779–781. [Google Scholar] [CrossRef]
- Koumakis, N.; Laurati, M.; Egelhaaf, S.U.; Brady, J.F.; Petekidis, G. Yielding of Hard-Sphere Glasses during Start-Up Shear. Phys. Rev. Lett. 2012, 108, 098303–098307. [Google Scholar] [CrossRef] [Green Version]







| Sample ID | a | b | c | d | e | f |
|---|---|---|---|---|---|---|
| Annealing temperature (K) | cast | 550 | 600 | 650 | 650 | 650 |
| Annealing time (min) | 0 | 30 | 30 | 30 | 120 | 1440 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M. Effect of Annealing on Strain Rate Sensitivity of Metallic Glass under Nanoindentation. Metals 2020, 10, 1063. https://doi.org/10.3390/met10081063
Li M. Effect of Annealing on Strain Rate Sensitivity of Metallic Glass under Nanoindentation. Metals. 2020; 10(8):1063. https://doi.org/10.3390/met10081063
Chicago/Turabian StyleLi, Mingcan. 2020. "Effect of Annealing on Strain Rate Sensitivity of Metallic Glass under Nanoindentation" Metals 10, no. 8: 1063. https://doi.org/10.3390/met10081063
APA StyleLi, M. (2020). Effect of Annealing on Strain Rate Sensitivity of Metallic Glass under Nanoindentation. Metals, 10(8), 1063. https://doi.org/10.3390/met10081063