Influence of Ring-Shaped Beam Profiles on Process Stability and Productivity in Laser-Based Powder Bed Fusion of AISI 316L
Abstract
:1. Introduction
2. Materials and Methods
2.1. Feedstock Material
2.2. Job Design
2.3. Experimental System
2.4. Process Parameters
2.5. Component Properties
2.5.1. Cross-Sectional Geometries
- Regular: The weld track topology is homogenous and smooth.
- Keyholing → A = δw/ww > 0.8: The aspect ratio of the welding penetration depth to width of the weld track is greater than 0.8 [24]. Increased energy input can cause a vapor capillary (“keyhole”) to form in the melt pool, which causes the high aspect ratios.
- Protrusion and depression: The topology of the corresponding weld tracks is characterized by protrusions in the center and depressions on the sides of the weld tracks. This weld track shape is created by long melt pools with increased backward flow of the molten material due to the Marangoni effect and recoil pressure [28]. Plateau–Rayleigh instability [25,27] causes the melt pool to form a protrusion that solidifies before it can break into individual melt balls.
- Undermelting → δw < 40 µm: The welding penetration depth is less than the powder layer thickness (40 μm in this study). In such weld tracks, the energy applied is usually too low.
2.5.2. Roughness Measurement
3. Results and Discussion
3.1. Influence of Laser Power and Scanning Speed on Melt Pool Geometry for Single Tracks
3.2. Influence of Laser Power, Scanning Speed, and Hatch Distance on Relative Overlap, Molten Cross-Sectional Area, and Molten Volume per Time
4. Conclusions
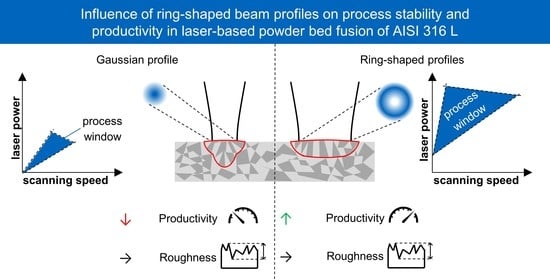
- The PBF-LB/M process itself can be stabilized at high laser powers and scanning speeds using ring-shaped beam profiles. Due to the reduction of process-limiting phenomena such as keyholing and balling, the process window for ring-shaped beam profiles increases significantly
- The process windows shift to higher laser powers when using ring-shaped profiles due to the larger beam diameters and thus decreasing intensities.
- An influence of the beam profiles on the degree of coupling of the laser energy is not found. For equal line energies, comparable cross-sectional areas are melted irrespective of the beam profile.
- When manufacturing multi-track segments, optimum area energies between 2 and 4 J/mm3 are identified for processing AISI 316L, independent of the beam profile used.
- In the experiments, the molten volume per time can be increased from less than 12 mm3/s (for Gaussian beams) to 20 mm3/s (for ring-shaped profiles) with slightly reduced roughness Sa.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Symbol | Explanation | Unit |
| A | Aspect ratio | - |
| Am | Molten cross-sectional area | µm² |
| El | Line energy | J/mm |
| EA | Area energy | J/mm² |
| h | Hatch distance | µm |
| Or | Relative overlap | % |
| PLaser | Laser power | W |
| Sa | Roughness: Arithmetical mean height | µm |
| Sz | Roughness: Maximum height | µm |
| Vm | Molten volume per time | µm3/s |
| vscan | Scanning speed | mm/s |
| ww | Width of the weld track | µm |
| w0 | Spot radius | µm |
| δw | Welding penetration depth | µm |
| Abbreviation | Explanation | |
| PBF-LB/M | Laser-based powder bed fusion of metals | |
| VBPP | Variable Beam Parameter Product | |
References
- Khorasani, A.; Gibson, I.; Veetil, J.K.; Ghasemi, A.H. A review of technological improvements in laser-based powder bed fusion of metal printers. Int. J. Adv. Manuf. Technol. 2020, 108, 191–209. [Google Scholar] [CrossRef]
- Yadroitsev, I.; Smurov, I. Selective laser melting technology: From the single laser melted track stability to 3D parts of complex shape. Phys. Procedia 2010, 5, 551–560. [Google Scholar] [CrossRef] [Green Version]
- Gusarov, A.V.; Grigoriev, S.N.; Volosova, M.A.; Melnik, Y.A.; Laskin, A.; Kotoban, D.V.; Okunkova, A.A. On productivity of laser additive manufacturing. J. Mater. Process. Technol. 2018, 261, 213–232. [Google Scholar] [CrossRef]
- Matthews, M.J.; Guss, G.; Khairallah, S.A.; Rubenchik, A.M.; Depond, P.J.; King, W.E. Denudation of metal powder layers in laser powder bed fusion processes. Acta Mater. 2016, 114, 33–42. [Google Scholar] [CrossRef] [Green Version]
- Gusarov, A.V.; Yadroitsev, I.; Bertrand, P.; Smurov, I. Heat transfer modelling and stability analysis of selective laser melting. Appl. Surf. Sci. 2007, 254, 975–979. [Google Scholar] [CrossRef]
- Kruth, J.P.; Froyen, L.; van Vaerenbergh, J.; Mercelis, P.; Rombouts, M.; Lauwers, B. Selective laser melting of iron-based powder. J. Mater. Process. Technol. 2004, 149, 616–622. [Google Scholar] [CrossRef]
- Rasch, M.; Roider, C.; Kohl, S.; Strauß, J.; Maurer, N.; Nagulin, K.Y.; Schmidt, M. Shaped laser beam profiles for heat conduction welding of aluminium-copper alloys. Opt. Lasers Eng. 2019, 115, 179–189. [Google Scholar] [CrossRef]
- Wischeropp, T.M.; Tarhini, H.; Emmelmann, C. Influence of laser beam profile on the selective laser melting process of AlSi10Mg. J. Laser Appl. 2020, 32, 22059. [Google Scholar] [CrossRef]
- Roehling, T.T.; Shi, R.; Khairallah, S.A.; Roehling, J.D.; Guss, G.M.; McKeown, J.T.; Matthews, M.J. Controlling grain nucleation and morphology by laser beam shaping in metal additive manufacturing. Mater. Des. 2020, 195, 109071. [Google Scholar] [CrossRef]
- Ayoola, W.A.; Suder, W.J.; Williams, S.W. Effect of beam shape and spatial energy distribution on weld bead geometry in conduction welding. Opt. Laser Technol. 2019, 117, 280–287. [Google Scholar] [CrossRef]
- Zhirnov, I.V.; Podrabinnik, P.A.; Okunkova, A.A.; Gusarov, A.V. Laser beam profiling: Experimental study of its influence on single-track formation by selective laser melting. Mech. Ind. 2015, 16, 709. [Google Scholar] [CrossRef] [Green Version]
- Metel, A.; Stebulyanin, M.; Fedorov, S.; Okunkova, A. Power density distribution for laser additive manufacturing (SLM): Potential, fundamentals and advanced applications. Technologies 2019, 7, 5. [Google Scholar] [CrossRef] [Green Version]
- Okunkova, A.; Volosova, M.; Peretyagin, P.; Vladimirov, Y.; Zhirnov, I.; Gusarov, A.V. Experimental approbation of selective laser melting of powders by the use of non-gaussian power density distributions. Phys. Procedia 2014, 56, 48–57. [Google Scholar] [CrossRef] [Green Version]
- Okunkova, A.A.; Peretyagin, P.; Podrabinnik, P.A.; Zhirnov, I.V.; Gusarov, A.V. Development of laser beam modulation assets for the process productivity improvement of selective laser melting. Procedia IUTAM 2017, 23, 177–186. [Google Scholar] [CrossRef]
- Schleifenbaum, H.; Meiners, W.; Wissenbach, K.; Hinke, C. High power selective laser melting: A new approach for individualized series production. In International Congress on Applications of Lasers & Electro-Optics, Proceedings of the ICALEO® 2009: 28th International Congress on Laser Materials Processing, Laser Microprocessing and Nanomanufacturing, Orlando, FL, USA, 2–5 November 2009; Laser Institute of America: Orlando, FL, USA, 2009; pp. 385–394. ISBN 978-0-912035-59-8. [Google Scholar]
- Loh, L.E.; Liu, Z.H.; Zhang, D.Q.; Mapar, M.; Sing, S.L.; Chua, C.K.; Yeong, W.Y. Selective laser melting of aluminium alloy using a uniform beam profile. Virtual Phys. Prototyp. 2014, 9, 11–16. [Google Scholar] [CrossRef]
- Wang, L.; Mohammadpour, M.; Gao, X.; Lavoie, J.-P.; Kleine, K.; Kong, F.; Kovacevic, R. Adjustable Ring Mode (ARM) laser welding of stainless steels. Opt. Lasers Eng. 2021, 137, 106360. [Google Scholar] [CrossRef]
- Havrilla, D.L.; Feuchtenbeiner, S.; Speker, N.; Haug, P.; Hesse, T. BrightLine weld-spatter reduced high speed welding with disk lasers. In High-Power Laser Materials Processing: Applications, Diagnostics, and Systems VII; Kaierle, S., Heinemann, S.W., Eds.; SPIE: Bellingham, WA, USA, 2018; p. 11. ISBN 9781510615359. [Google Scholar]
- Maina, M.R.; Okamoto, Y.; Okada, A.; Närhi, M.; Kangastupa, J.; Vihinen, J. High surface quality welding of aluminum using adjustable ring-mode fiber laser. J. Mater. Process. Technol. 2018, 258, 180–188. [Google Scholar] [CrossRef]
- Mohammadpour, M.; Wang, L.; Kong, F.; Kovacevic, R. Adjustable ring mode and single beam fiber lasers: A performance comparison. Manuf. Lett. 2020, 25, 50–55. [Google Scholar] [CrossRef]
- He, Y.; Zhong, M.; Beuth, J.; Webler, B. A study of microstructure and cracking behavior of H13 tool steel produced by laser powder bed fusion using single-tracks, multi-track pads, and 3D cubes. J. Mater. Process. Technol. 2020, 286, 116802. [Google Scholar] [CrossRef]
- nLIGHT, Inc. AFX-1000: Programmable Fiber Lasers for Additive Manufacturing. 2018. Available online: https://www.optoprim.de/PDF/nLIGHT/nLIGHT_AFX-1000_datasheet.pdf (accessed on 1 December 2021).
- DIN German Institute for Standardization. DIN EN ISO 11146-1:2005-04, Lasers and Laser-Related Equipment—Test Methods for Laser Beam Widths, Divergence Angles and Beam Propagation Ratios—Part 1: Stigmatic and Simple Astigmatic Beams (ISO 11146-1:2005); German version EN ISO 11146-1:2005; Beuth Verlag GmbH: Berlin, Germany, 2005. [Google Scholar]
- Tenbrock, C.; Fischer, F.G.; Wissenbach, K.; Schleifenbaum, J.H.; Wagenblast, P.; Meiners, W.; Wagner, J. Influence of keyhole and conduction mode melting for top-hat shaped beam profiles in laser powder bed fusion. J. Mater. Process. Technol. 2020, 278, 116514. [Google Scholar] [CrossRef]
- Brandt, M. Laser Additive Manufacturing: Materials, Design, Technologies, and Applications; Woodhead Publishing: Shaxton, UK, 2016. [Google Scholar]
- Markl, M.; Körner, C. Multiscale modeling of powder bed–based additive manufacturing. Annu. Rev. Mater. Res. 2016, 46, 93–123. [Google Scholar] [CrossRef]
- Khairallah, S.A.; Anderson, A. Mesoscopic simulation model of selective laser melting of stainless steel powder. J. Mater. Process. Technol. 2014, 214, 2627–2636. [Google Scholar] [CrossRef]
- Zhang, T.; Li, H.; Liu, S.; Shen, S.; Xie, H.; Shi, W.; Zhang, G.; Shen, B.; Chen, L.; Xiao, B.; et al. Evolution of molten pool during selective laser melting of Ti–6Al–4V. J. Phys. D Appl. Phys. 2019, 52, 55302. [Google Scholar] [CrossRef]
- Heinl, M.; Greiner, S.; Wudy, K.; Pobel, C.; Rasch, M.; Huber, F.; Papke, T.; Merklein, M.; Schmidt, M.; Körner, C.; et al. Measuring procedures for surface evaluation of additively manufactured powder bed-based polymer and metal parts. Meas. Sci. Technol. 2020, 31, 95202. [Google Scholar] [CrossRef]
- DIN German Institute for Standardization. DIN EN ISO 25178-2:2012-09, Geometrische Produktspezifikation (GPS)—Oberflächenbeschaffenheit: Flächenhaft—Teil_2: Begriffe und Oberflächen-Kenngrößen (ISO 25178-2:2012); Deutsche Fassung EN_ISO_25178-2:2012; Beuth Verlag GmbH: Berlin, Germany, 2012. [Google Scholar]
- Grünberger, T.; Domröse, R. Direct Metal Laser Sintering. Laser Tech. J. 2015, 12, 45–48. [Google Scholar] [CrossRef]
- Paschotta, R. Thermal Lensing. RP Photonics Encyclopedia. Available online: https://www.rp-photonics.com/thermal_lensing.html (accessed on 1 December 2021).
- Wischeropp, T.M.; Salazar, R.; Herzog, D.; Emmelmann, C. Simulation of the effect of different laser beam intensity profiles on heat distribution in selective laser melting. In Lasers in Manufacturing Conference, June 22–25; WLT: Munich, Germany, 2015. [Google Scholar]
- Di, W.; Yongqiang, Y.; Xubin, S.; Yonghua, C. Study on energy input and its influences on single-track, multi-track, and multi-layer in SLM. Int. J. Adv. Manuf. Technol. 2012, 58, 1189–1199. [Google Scholar] [CrossRef]
- Dong, Z.; Liu, Y.; Wen, W.; Ge, J.; Liang, J. Effect of Hatch Spacing on Melt Pool and As-built Quality During Selective Laser Melting of Stainless Steel: Modeling and Experimental Approaches. Materials 2019, 12, 50. [Google Scholar] [CrossRef] [PubMed] [Green Version]














| Profile Name VBPP | Peak Power | Ring Power | Spot Diameter 2w0 |
|---|---|---|---|
| 0 | 100% | 0% | 107 µm |
| 4 | 40% | 60% | 253 µm |
| 5 | 20% | 80% | 262 µm |
| 6 | 10% | 90% | 271 µm |
| Gaussian Profile (VBPP 0) | Ring-Shaped Profiles (VBPP 4, 5, 6) | ||
|---|---|---|---|
| Laser Power PLaser in W | Scanning Speed vscan in mm/s | Laser Power PLaser in W | Scanning Speed vscan in mm/s |
| 200 | 500, 800, 1100, 1400, 1700 | 300 | 500, 800, 1100, 1400, 1700 |
| 300 | 500, 800, 1100, 1400, 1700 | 450 | 500, 800, 1100, 1400, 1700 |
| 400 | 500, 800, 1100, 1400, 1700 | 600 | 500, 800, 1100, 1400, 1700 |
| 450 | 500, 800, 1100, 1400, 1700 | 750 | 500, 800, 1100, 1400, 1700 |
| 500 | 500, 800, 1100, 1400, 1700 | 900 | 500, 800, 1100, 1400, 1700 |
| 600 | 500, 800, 1100, 1400, 1700 | 1050 | 500, 800, 1100, 1400, 1700 |
| Gaussian Profile (VBPP 0) | Ring-Shaped Profiles (VBPP 4, 5, 6) | ||||
|---|---|---|---|---|---|
| Laser Power PLaser in W | Scanning Speed vscan in mm/s | Hatch Distance h in µm | Laser Power PLaser in W | Scanning Speed vscan in mm/s | Hatch Distance h in µm |
| 200 | 500, 800, 1100, 1400 | 85, 120, 155 | 450 | 500, 800, 1100, 1400 | 170, 240, 310 |
| 300 | 500, 800, 1100, 1400 | 85, 120, 155 | 600 | 500, 800, 1100, 1400 | 170, 240, 310 |
| 400 | 500, 800, 1100, 1400 | 85, 120, 155 | 750 | 500, 800, 1100, 1400 | 170, 240, 310 |
| 500 | 800, 1100, 1400, 1700 | 85, 120, 155 | 900 | 800, 1100, 1400, 1700 | 170, 240, 310 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grünewald, J.; Gehringer, F.; Schmöller, M.; Wudy, K. Influence of Ring-Shaped Beam Profiles on Process Stability and Productivity in Laser-Based Powder Bed Fusion of AISI 316L. Metals 2021, 11, 1989. https://doi.org/10.3390/met11121989
Grünewald J, Gehringer F, Schmöller M, Wudy K. Influence of Ring-Shaped Beam Profiles on Process Stability and Productivity in Laser-Based Powder Bed Fusion of AISI 316L. Metals. 2021; 11(12):1989. https://doi.org/10.3390/met11121989
Chicago/Turabian StyleGrünewald, Jonas, Florian Gehringer, Maximilian Schmöller, and Katrin Wudy. 2021. "Influence of Ring-Shaped Beam Profiles on Process Stability and Productivity in Laser-Based Powder Bed Fusion of AISI 316L" Metals 11, no. 12: 1989. https://doi.org/10.3390/met11121989
APA StyleGrünewald, J., Gehringer, F., Schmöller, M., & Wudy, K. (2021). Influence of Ring-Shaped Beam Profiles on Process Stability and Productivity in Laser-Based Powder Bed Fusion of AISI 316L. Metals, 11(12), 1989. https://doi.org/10.3390/met11121989