Selective Laser Melting of 316L Austenitic Stainless Steel: Detailed Process Understanding Using Multiphysics Simulation and Experimentation

Abstract

The parameter sets used during the selective laser melting (SLM) process directly affect the final product through the resulting melt-pool temperature. Achieving the optimum set of parameters is usually done experimentally, which is a costly and time-consuming process. Additionally, controlling the deviation of the melt-pool temperature from the specified value during the process ensures that the final product has a homogeneous microstructure. This study proposes a multiphysics numerical model that explores the factors affecting the production of parts in the SLM process and the mathematical relationships between them, using stainless steel 316L powder. The effect of laser power and laser spot diameter on the temperature of the melt-pool at different scanning velocities were studied. Thus, mathematical expressions were obtained to relate process parameters to melt-pool temperature. The resulting mathematical relationships are the basic elements to design a controller to instantly control the melt-pool temperature during the process. In the study, test samples were produced using simulated parameters to validate the simulation approach. Samples produced using simulated parameter sets resulting in temperatures of $2000\left(\mathrm{K}\right)$ and above had acceptable microstructures. Evaporation defects caused by extreme temperatures, unmelted powder defects due to insufficient temperature, and homogenous microstructures for suitable parameter sets predicted by the simulations were obtained in the experimental results, and the model was validated.

1. Introduction

Additive manufacturing (AM) technology builds parts layer by layer using powders as a medium in 3D printers. The powders are exposed to a heat source and are melted. Referring to the manufacturing method, the heat source could be a laser or electron beam. It can be regarded as a revolution in fabrication technologies due to its superior advantages. AM technology leads the part directly from design to production. It reduces the need for conventional methods like casting and punching and enables building complex parts directly. Fabrication with additive technology reduces the need for large assembly and allows manufacture of unique parts in assemblies [1,2]. One of the most favorable techniques of additive manufacturing technology is selective laser melting (SLM). In the SLM process, a layer of powder is spread on the build plate. The laser beam respecting the pattern which is designed and imported to the machine scans the powder layer, and the process repeats for every layer, and finally, the part will be ready for post-processes if needed [3,4,5].

The properties of the final product, especially its metallurgical properties, are affected by various parameters, of which the most important one is the formed temperature during the printing [6]. Subsequently, the forming temperature is affected by various factors such as laser power, scanning velocity, laser spot diameter, powder size, preheating, and laser beam properties. Keeping the temperature constant and preventing deviation of temperature from the specified value is also necessary for having a homogeneous and uniform structure [7,8]. Currently, the suitable process parameters which lead to a desired microstructure are often extracted by the experimental methods which are highly costly and time-consuming. A reliable model will able us to extract the process parameters at very low cost and in little time. The suitable process parameters will result in a final product with minimum defects. Zhang et al. [9] investigated a thermal model to study the melt-pool of alumina ceramics. They showed that the laser power and the scanning velocity influence the maximum temperature, lifetime, dimensions, and temperature gradients of the melt-pool. Bruna-Rosso et al. [10] developed a model to compute the thermal field in millimeter-scale together with the consequent melt-pool dimension and temperature, and the model was validated with high-speed imaging. A two-dimensional finite difference model was developed by Foteinopoulos et al. [11] to calculate the temperature of a part in each time step, and employed an algorithm for node birth and distance adaptation over time to reduce the computational time.

However, it is not possible to obtain the true and error-free temperature of the weld pool without considering the driving forces in the weld pool. In other words, modeling the process only as a thermal model is not realistic, and it needs to contribute the convection in the flow to the model. Leitz et al. [12] studied the effect of the laser power and laser energy density on the melt-pool width by developing a multiphysics model. They figured out that the melt-pool dimensions are wider in steel compared to the molybdenum because of the thermal conductivity difference in materials. Artinov et al. [13] developed a multiphysics model to calculate a reliable equivalent heat source and to predict the thermal behavior during the laser welding using a moving mesh and weak constraints. Bayat et al. [14] investigated a multiphysics model for laser-based powder bed fusion to study the keyhole phenomena in the melting of Ti6Al4V and confirmed their work by doing an X-CT analysis. Courtois et al. [15] simulated the SLM and keyhole formation with a new approach. They took the reflection of the laser beam in the keyhole into account. Finally, they compared the melt-pool shapes resulting from modeling with experimental micrographs. T. Mukherjee et al. [16] developed a three-dimensional (3D), transient, heat transfer, and fluid flow model to calculate temperature and velocity fields, build shape and size, cooling rates, and the solidification parameters during the PBF process. Shi, Xuezhi, et al. [17] developed a single-track method for parameter optimization of Ti-47Al-2Cr-2Nb powder in SLM. Using the single-track scan results, they developed a parameter window and optimized the fabrication parameters for Ti-47Al-2Cr-2Nb powder. They also built regression models to predict the geometric characteristics of single tracks. The listed works do not suppose a certain process parameter window and do not comprise a sample part experimental task. Almost all of their experimental confirmation is done in single layer scanning, not sample part fabrication, which includes the previous and next layers’ effect. As such, these models are presented only as developed models, and there is a significant gap in the development of various process parameters and the relationships between them and their application for sustainable performance during printing. That is to say, what are still missing, are the various process parameter sets and the mutual relationships between them. These have been obtained via a reliable model that presents us the temperature values considering the melt process’s effective aspects.

The special properties of austenitic steels make them the most popular group of high-alloy stainless steels. The contribution of various alloy elements gives them a very important and notable feature in the laser powder bed fusion: their weldability and usefulness allocate a special space for them in additive manufacturing, and 316L stainless steel, as austenitic steel, stands out with its perfect resistance to oxidation at high temperatures while maintaining a low coefficient of thermal expansion, creep resistance, resistance to fatigue, and heat resistance [18,19,20,21].

Based on these issues, the paper develops vast sets of the process parameters and the mathematical relationship between them for suitable and controllable fabrication using stainless steel 316L powder. A 3D multiphysics model is developed. The model solves three equations of heat transfer, conservation of mass, and time-dependent momentum by using temperature-dependent material properties. The volumetric moving heat source is included in heat transfer physics, and driving forces are considered in fluid flow physics. The model presents parameter sets and discusses the microstructure (defects) of samples fabricated by employing extracted parameters. In addition, the mathematical relationships between laser power, laser spot diameter, and temperature of the melt-pool are developed. These relationships allow one to predict the temperature and consequently to predict the part structure. The mathematical relationships are the basis of the controller design to form a sustainable melt-pool temperature during the printing process and to simultaneously achieve a final designed part with a minimum defect and homogeneous microstructure.

Although the process parameters applicable to 3D printing of 316L stainless steel to obtain dense structures are available in the literature, the method proposed in this study has the following advantages:

• The proposed approach develops parameter sets by simulating multiphysics phenomena between the energy source and powder interaction. Therefore, comprehensive process parameter windows containing sensitive process parameters could be obtained for adding a promising numerical model to the literature.
• The numerical model is developed using more than one type of physics. Rather than using heat transfer physics only, laminar flow physics is also included into the simulation which gives a more realistic approach to the SLM operation.
• Direct mathematical relationships between process parameters are developed to instantly compute the melt-pool maximum temperature. These mathematical relationships could be used as the basic elements in the controller design of the 3D printer machine to control the melt-pool temperature during the process.

2. Selective Laser Melting

The selective laser melting (SLM) process is the powder laser-based interaction process that is generally performed on a building plate. The product CAD file is imported to the 3D printer, and the proper process parameters are used to build the part accordingly. As illustrated in Figure 1, an appropriate amount of powder is spread on the building plate by powder roller, and the laser beam is exposed to the powder selectively according to the part geometry. At the end of each layer, the powder delivery piston moves one step/layer up, and the fabrication piston moves one step down. The process continues until the last layer is printed, and the process is finished accordingly. A high enough energy laser beam is exposed to the powder to reach the melting point. Powders are completely melted and then solidified to compose the part during which phase transformations are introduced. The process is performed in a gaseous atmosphere in which the material of gas is adjusted depending on the powder material [22].

3. Equations Governing SLM Process

The mathematical model has been established to simulate laser and powder interaction in a 3D environment. Given the laser energy source, $Q_{Laser}$, the temperature and temperature gradient field relationship is described by the energy Equation (1), which can be numerically solved to simulate the temperature change in the SLM process:

$$\rho C_p^{*}\frac{\partial T}{\partial t}+\rho C_p^{*}u·\nabla T=\nabla ·\left(k\nabla T\right)+A{Q}_{Laser}+Q_{Rad}+Q_{ev}$$

(1)

where $\rho$, $C_p{}^{*}$, $T$, $t$, $u$,$k$, $A, Q_{Laser}$, $Q_{Rad}$, and $Q_{ev}$ are density $\left(\mathrm{kg}/{\mathrm{m}}^3\right)$, modified specific heat capacity $(\mathrm{J}/\mathrm{kg}·\mathrm{K})$, temperature $\left(\mathrm{K}\right)$, time $\left(\mathrm{s}\right)$, velocity $\left(\mathrm{m}/\mathrm{s}\right)$, thermal conductivity $\left(\mathrm{W}/\left(\mathrm{m}·\mathrm{K}\right)\right)$, absorption coefficient (-), input laser energy source $(\mathrm{W}/{\mathrm{m}}^3)$, radiated energy source $(\mathrm{W}/{\mathrm{m}}^2)$, and evaporation heat loss $(\mathrm{W}/{\mathrm{m}}^3)$, respectively. Shadowing effect, multi-reflection, and beam angle effect on the absorption of the laser are neglected [12].

Since the heat source determines the generated energy of laser power and leads to temperature build-up in the melt-pool, it is important to select an appropriate heat source model. The forming temperature would affect the microstructure and the mechanical structure of the final product, so the heat source model should be the nearest model to reality. The models may be introduced as two-dimensional or three-dimensional. The two-dimensional Gaussian model involves only the distribution of heat in x and y directions in time t. In reality, the laser beam acts in 3D and also penetrates the powders. The volumetric heat source [23] is developed to contribute to the penetration of the laser beam into the powders. Then it should involve the penetration direction in addition to the surface directions of the powders. The model used in this paper belongs to the absorptivity profile group, which is a volumetric Gaussian distribution model and involves the penetration of the laser beam into the powders [24,25]:

$$Q_{Laser}=\frac{I_0}{b} exp\left(\frac{-2r^2}{r_0^2}\right)exp\left(\frac{z-z_0}{b}\right)$$

(2)

$$I_0=\frac{2P}{\pi r_0{}^2}$$

(3)

where $I_0$, $b$, $r$, $r_0$, $z$, and $z_0$ are the intensity of the laser beam at the beam axis $(\mathrm{W}/{\mathrm{m}}^2)$, penetration distance of the laser beam $\left(\mathrm{m}\right)$, distance from the point to the center of the beam $\left(\mathrm{m}\right)$, the radius of the laser beam $\left(\mathrm{m}\right)$, the vertical position of the powder $\left(\mathrm{m}\right)$, the position of the top of powder $\left(\mathrm{m}\right)$, and $P$ denotes the laser power $\left(\mathrm{W}\right)$. The vertical position of the powder, $r \left(\mathrm{m}\right)$, shows the $x \left(\mathrm{m}\right)$and $y \left(\mathrm{m}\right)$ positions of every irradiated point at time $t\left(\mathrm{s}\right)$ ($r=\sqrt{x^2+y^2}$) through the scanning path with a scanning velocity of $v_x (\mathrm{m}/\mathrm{s})$ that is equal to $v_x=x/t$[9].

On the other hand, radiative heat loss is illustrated using the Stefan–Boltzmann law, which is nonlinear and is denoted by:

$$Q_{Rad}=-\mathsf{\epsilon }\sigma \left(T^4-T_0^4\right)$$

(4)

where $\mathsf{\epsilon }$, $\sigma$, and $T_0$ are the emissivity of the powder (-), Stefan–Boltzmann constant for radiation $(5.67\times {10}^{-8}(\mathrm{W}/{\mathrm{m}}^2·{\mathrm{K}}^4))$, and ambient temperature (K), respectively. Evaporation heat loss is also introduced, which is determined through the following Equation [26]:

$$Q_{ev}=-\frac{H_{ev}{m}^{•}}{h}$$

(5)

where $H_{ev}$, $m^{•}$, and $h$ are latent heat of evaporation $\left(\mathrm{J}/\mathrm{kg}\right)$, evaporation rate $\left(1/\mathrm{s}\right)$, and mesh size (m), respectively. Referring to the Hertz–Knudsen equation, the evaporation rate is determined as [27]:

$$m^{•}=\left(p_v\left(T\right)-p_0\right)\sqrt{\frac{M}{2\pi RT}}$$

(6)

where $p_{v }\left(\mathrm{T}\right)$, $p_0$, $M$, and $R$ are vapor pressure $\left(\mathrm{N}/{\mathrm{m}}^2\right)$ at the temperature of $T$ $\left(\mathrm{K}\right)$, ambient pressure $\left(\mathrm{N}/{\mathrm{m}}^2\right)$, molar mass $\left(\mathrm{kg}/\mathrm{mol}\right)$, and ideal gas constant $\left(\mathrm{J}/\mathrm{mol}·\mathrm{K}\right)$, respectively. The vapor pressure at the temperature of $T$ can be determined from the following Equation [27]:

$$p_v\left(T\right)=p_0{e}^{\frac{H_{ev}M}{R{T}_{ev}}\left(1-\frac{T_{ev}}{T}\right)}$$

(7)

where $T_{ev}$ is the evaporation temperature $\left(\mathrm{K}\right)$.

As powder absorbs heat energy from the laser beam, it melts, and phase transformation occurs from solid to liquid. Here, fluid flow physics solves the conservation of mass and momentum equations. The equations are:

$$\nabla ·u=0$$

(8)

$$\rho \left(\frac{\partial u}{\partial t}+u\left(\nabla ·u\right)\right)=\nabla ·\left[-pI+\mu \left(\nabla u+{\left(\nabla u\right)}^T\right)\right]+\rho g+F$$

(9)

where $I$, $\mu$, ${\left(·\right)}^T$, $g$, and $F$ are pressure $\left(\mathrm{N}/{\mathrm{m}}^2\right)$, identity matrix, viscosity $\left(\mathrm{Pa}·\mathrm{s}\right)$, transposed matrix, gravity $\left(\mathrm{m}/{\mathrm{s}}^2\right)$, and volume force $\left(\mathrm{N}/{\mathrm{m}}^3\right)$, respectively [13].

The volume force contains four terms involved in buoyancy force (first term), Carman–Kozeny equation (second term), surface tension force (third term), and Marangoni effect (fourth term) as [16,28,29]:

$$F=\rho g\beta \left(T-T_m\right)-A_1\left(\frac{{\left(1-f_l\right)}^2}{f_l{}^3+A_2}\right)+\kappa \gamma n+{\nabla }_s\gamma$$

(10)

where $\beta$, $T_m$, $\kappa$, $\gamma$, $n$, and ${\nabla }_s$ are coefficients of thermal expansion $\left(1/\mathrm{K}\right)$, melting temperature $\left(\mathrm{K}\right)$, curvature of interface, surface tension coefficient $\left(\mathrm{N}/\mathrm{m}\right)$, unit normal to the local surface, and surface gradient operator, respectively. The buoyancy force is the deviation of the density during changing temperature.

Carman–Kozeny equation defines the mushy zone. The transition from the solid phase to the liquid phase takes place during a temperature interval, which is named the melting interval ($\delta T$). During this interval, the metal is a mixture of the solid and liquid phases. This mixed region is named the mushy zone [29].$A_1$ is a huge constant that is defined to fix the powders under melting temperature as a solid phase, and $A_2$ is a small constant to satisfy the convergence during the simulation. Since the liquid fraction $(f_l)$ is zero under the liquidus temperature $(T_l)$, the presence of $A_2$ in this case does not allow the denominator to be zero. This damping force acts only in the mushy and solid-state of the material and vanishes in the liquid phase. The vanishing occurs linearly, along $f_l$, which changes linearly with respect to the solidus temperature ($T_s$) and liquidus temperature,

$$f_l=\left\{\begin{array}{c}0 if T<T_l\\ \frac{T-T_s}{T_l-T_s} if T_s\le T\le T_l\\ 1 if T>T_l\end{array}\right.$$

(11)

Conversely to melting, when the solidification of molten metal starts, respectively this force starts to grow and act on the solidified metal. As an alternative to the Carman–Kozeny force, powders can be assumed as a highly viscous fluid material in the solid phase in simulations. Parallel use of these two ways can be used as well, however, this may present convergence difficulties. Here, the simulations have been performed by applying the Carman–Kozeny force only.

The melt-pool surface indicates a free surface, which is defined as an open boundary. The Marangoni effect is a result of spatial variation of the surface tension coefficient due to temperature gradients. The surface tension acts as normal, and the Marangoni effect applies a tangential force on the surface. In simulations, the molten flow was assumed to be laminar and incompressible.

The present study uses the above-introduced multiphysical phenomena to simulate the powder–laser beam interaction. Although the use of these equations has been reported before, the main of objective of our study was to find out an allowable process parameter set for the SLM additive manufacturing of a given material.

4. Multiphysics Model

The multiphysics model described in Section 3 was used to simulate the metal powder–laser interaction. A three-dimensional model was designed, and a time-dependent study was used. Considering the powder size distribution in the datasheet of the Concept Laser (Concept Laser, Lichtenfels, Germany) and the practical layer thickness during the manufacturing, the average diameter of powders was considered 40 μm (layer thickness). Then powders were modeled as homogeneous 40 μm spheres, which were assumed to be homogeneously distributed on the built plate. Simulations were done in one path of 720 μm distance and the model was formulated symmetrically to reduce the calculation time in the simulations.

Simulation was done by coupling heat transfer and laminar flow physics of the commercial finite element software COMSOL Multiphysics 5.4 (COMSOL Inc., Burlington, MA, USA). A free tetrahedral mesh was used for all domains, and a mesh size of 5 microns was used. The volumetric heat source, radiative, and evaporation heat loss heat boundaries were employed, and incompressible flow patterns with gravity force, buoyancy force, Carman–Kozeny force, surface tension force, and Marangoni effect were applied. Computation times were found to be in a range of 6–15 h for a scanning track of 720 μm on two cores of a dual CPU Intel Xeon Gold 6230 CPU workstation. The chemical composition of the material used in the simulation, which was obtained employing the XRF and combustion analysis, is given in

Table 1. Chemical composition of stainless steel 316L powder [30].

Element	C	Mn	Si	Ni	Cr	Mo	S	P	Fe
Mass.-%	$0.021$	$0.95$	$0.73$	$12.9$	$17.8$	$2.28$	$0.005$	$<0.045$	Balance

.

One of the most important factors in the modeling was the temperature-dependent material properties.

Table 2. Material properties of stainless steel 316L [31,32,33].

Material Property	Symbol	Value	Unit
Melting Temperature	$T_m$	$1650$	$\mathrm{K}$
Melting Interval	$\delta T$	$\pm 10$	$\mathrm{K}$
Evaporation Temperature	$T_{ev}$	$3086$	$\mathrm{K}$
Latent Heat of Melting	$H_m$	$2.8\times {10}^5$	$\mathrm{J}/\mathrm{kg}$
Latent Heat of Evaporation	$H_{ev}$	$6.1\times {10}^6$	$\mathrm{J}/\mathrm{kg}$
Density	$\rho$	$7700 \left(solid\right)-8000 \left(liquid\right)$	$\mathrm{kg}/{\mathrm{m}}^3$
Thermal Conductivity	$k$	$11.82+1.06\times {10}^{-2}T$	$\mathrm{W}/\mathrm{m}·\mathrm{K}$
Specific Heat Capacity	$C_p$	$330.9+0.563T-4.015\times {10}^{-4} T^2+9.465\times {10}^{-8} T^3$	$\mathrm{J}/\mathrm{kg}·\mathrm{K}$
Absorption Coefficient	$A$	$0.55 \left(solid\right)-0.3 \left(liquid\right)$	$-$
Marangoni Coefficient	$\raisebox{1ex}{$\mathrm{d}\mathsf{\gamma }$}\!\left/ \!\raisebox{-1ex}{$\mathrm{dT}$}\right.$	$-0.40\times {10}^{-3}$	$\mathrm{N}/\mathrm{m}·\mathrm{K}$

shows the material properties used for stainless steel 316L in the model [31,32,33]. Convergence is a noteworthy point during simulations. There are different solvers to solve equations numerically in software, such as the fully coupled and segregated solvers. This paper used a segregated solver (a tolerance factor of 0.005) to solve the mentioned three equations applying the Newton–Raphson iteration (a minimum damping factor of ${10}^{-6}$) until the solution was converged. The software, in every time step, first calculated the temperature in heat transfer physics. Then, it passed to the laminar flow physic and there, employing the achieved temperature too, calculated the velocity and pressure. If it converged, the computation continued to the next time step, otherwise, it repeated the cycle until the convergence was complete.

Although finite element methods are widely used to simulate the additive manufacturing processes, the main expectations of simulations are either to decide the scanning strategy or to predict the melt-pool. In this study, the multiphysics simulation model was used to reveal the effects of laser power, $P$ in $\left(\mathrm{W}\right)$, the radius of the laser beam, or laser spot diameter-, $r_0$ in $\left(\mathsf{\mu }\mathrm{m}\right)$, and velocity -, $u$, $\left(\mathrm{m}/\mathrm{s}\right)$ on the melting temperature. It is well known that these are some of the process parameters in SLM, which are mainly determined by doing a set of experiments.

5. Experimental Approach

To confirm the simulation results, experimental studies were performed at the Additive Manufacturing Technology Application and Research Center (EKTAM) of Gazi University. Experiments were done using a 3D printer of the Concept Laser-M2 CUSING (Concept Laser, Lichtenfels, Germany) model. The machine has a continuous wave Ipg Ylr 400 ac y14 ytterbium fiber laser ($\lambda =1070 \mathrm{nm}$) with a nominal maximum laser power of 400 W. Fabrication was done in a controlled build chamber under a nitrogen atmosphere which contained a maximum 0.4% ${\mathrm{O}}_2$. The base plate of the machine is steel with dimensions of 245 mm × 245 mm × 25 mm. The preparation process was carried out on the plate and it was made ready for production. The surface was ground with the FOREMAN ST4080A Surface Grinder (Sezginler Makina A.Ş., Bursa, Turkey) to have a plate with minimum roughness and maximum flatness. Next, the plate was sandblasted to prevent reflection.

The powders used for the fabrication were gas atomized Concept Laser SS 316L powders with a powder size distribution shown in

Table 3. Results of the sieve analysis of powders used for fabrication of samples [30].

Particle Size	$<100 \mathsf{\mu }\mathbf{m}$	$<80 \mathsf{\mu }\mathbf{m}$	$<63 \mathsf{\mu }\mathbf{m}$	$<45 \mathsf{\mu }\mathbf{m}$	$<32 \mathsf{\mu }\mathbf{m}$	$<20 \mathsf{\mu }\mathbf{m}$
Value (%)	$99.88$	$99.60$	$99.11$	$97.59$	$73.83$	$23.42$

and

Table 4. Powder size distribution of powders used for the fabrication of samples [30].

Parameter	Dv (10)	Dv (50)	Dv (90)	Width (90;10)
Unit	$\mathsf{\mu }\mathrm{m}$	$\mathsf{\mu }\mathrm{m}$	$\mathsf{\mu }\mathrm{m}$
Result	18.680	29.631	47.984	0.989

. Figure 2 shows an SEM image of the powders, which are almost spherical in structure.

Ten sets of parameters were selected from the results of the simulations, which are shown in later chapters. Using these parameters, a hatch space of $115 \mathsf{\mu }\mathrm{m}$ and powder layer of $25\mathsf{\mu }\mathrm{m}$, ten samples were fabricated, and their microstructures were examined to illustrate the conformity of the simulation results. The layer thickness was selected as 40 μm. In the fabrication process, the fabrication piston moved down 25 $\mathsf{\mu }\mathrm{m}$ in each layer to spread the powder for the upcoming layer. However, since the melted preview layer’s surface was a rough surface and included concavities, as the spread powder fills them too, the powder layer that should be scanned after powder delivery was therefore 40 $\mathsf{\mu }\mathrm{m}$. That was why the powder layer in the simulations was assumed to be 40 $\mathsf{\mu }\mathrm{m}$. Every sample was fabricated in 100 layers using the island scanning strategy, and their final dimensions were 80 mm $\times$10 mm $\times$2 mm. The produced samples were prepared under slice cutting to be ready for the microstructure inspection. Cutting was done with diamond micron wire at a very slow speed with water cooling to avoid affecting the microstructure. The method of cutting and preparing samples for microstructure inspection is shown in detail in the Supplementary Materials. The cross-section of the cut samples was polished using different metallographic sandpapers and etched with a proper reagent ($55\%\mathrm{HCl}, 20\%{\mathrm{NHO}}_3$ and $25\%$ methanol [34]) for the microstructure inspection. The optical micrographs were taken by DMi8 Leica Microsystems (Leica Microsystems, Wetzlar, Germany) microscope, and the scanning electron microscopy (SEM) was done by JSM-6060LV JEOL (JEOL Ltd., Tokyo, Japan).

6. Results and Discussion

The simulation model presents coupling of two types of physics, and the results are shown in Figure 3. An SLM process was simulated and melting during moving laser heat source was presented. The simulations were done in symmetry mode to reduce the calculations and process time. Basically, Figure 3 illustrates the temperature values of a powder layer for a given set of laser power, laser spot diameter, and scanning velocity. The symmetry view (Figure 3a) shows the laser beam penetration in powder, and the complete view (Figure 3b) shows a complete scanned row of powders. Isosurface temperature view (Figure 3c) and the phase change is depicted (Figure 3d). Figure 3d is an illustration of the melted area. The area with the value of one is the liquid phase, while the zero value area belongs to the solid phase. Indeed, the area with the value of one is the melt-pool area. The thin border area, which has a value between one and zero, is the mushy region as illustrated earlier.

Selecting proper process parameters is undoubtedly crucial for various aspects of additively manufactured parts. Optimal process parameters can reduce the cracking effect and reach fully density [35]. This also leads to optimum and adequate microstructure and mechanical properties [36]. Improper parameters will result in pores and spatters, leading to undesired mechanical properties; also, low speed of manufacturing or high fabrication costs will be encountered if improper process parameters are used. The investigated model enables us to simulate the process with selected parameters. That is to say, the model is a tool that we can use to predict the process parameters in the SLM.

Low melt-pool temperature will result in pores in the manufactured parts. Lack of fusion causes elongated and inconsistent pores. These defects refer to insufficient temperature in the melt-pool [37]. Through low temperature, there might be unmelted powders, which will lead to a part full of pore defects. On the other hand, extreme temperatures will result in defects such as spatter, overcooking, holes, and high heat tensions. Spatters come up due to evaporation force, which forces the melted metal to separate from the plane by overcoming surface tension. It leads to surface defects in layers. Accordingly, the temperature exceeding the evaporation temperature leads to undesirable products. Evaporation may lead to the formation of keyhole pores that are deeply embedded in the part [38]. However, fabrication speed is an important issue in the process; high scanning speeds lead to fast fabrication.

Referring to all the mentioned notes above, the most important goal is to reach a complete melting without evaporation. Indeed, the favorable parameters are a set of parameters that melt the distributed powder layer completely and also melt a part of the prior layers to make a proper bond between layers. For this purpose, the selected parameters should satisfy the melting phenomena all over the powder layer. The most critical area is the depth of the powder layer. If the parameter set produces enough temperature at a depth of the powder layer for melting, and meanwhile the parameter set does not lead to any evaporation at any part of the powder layer, this may be considered as a proper and satisfactory parameter set which does not cause any defects due to temperature deficiency or excess. Formation of the spatter and residual porosities are related and promoted by instability regimes at high energy density [39]. For this purpose, in this study, the maximum temperature was recorded at the depth of $40 \mathsf{\mu }\mathrm{m}$, since the powder layer thickness in experiments was $40\mathsf{\mu }\mathrm{m}$. To reveal the effects of different process parameters on the SLM additive manufacturing of stainless steel, the simulations have been carried out for the various sets of parameters.

6.1. Effect of Laser Power

Simulations were performed for four different scanning velocities. Referring to Equation (12), regarding Rosenthal’s equation, which approximates the temperature distribution of a single track in the SLM process [40], the relation between temperature and laser power, in a constant moving heat point source velocity, is a linear relationship. Figure 4 shows the simulation results and fitted curves of the powder layer temperature at various laser powers.

$$T\left(y\right)=\frac{AP}{2\pi rk}·exp\left(\frac{-v_x}{2\alpha }\right)$$

(12)

where $v_x\left(\mathrm{m}/\mathrm{s}\right)$ is the moving heat point source velocity and $\alpha$ is the thermal diffusivity $({\mathrm{m}}^2/\mathrm{s})$.

At each scanning velocity, temperature values were recorded after a steady state was achieved. Achieving the stability condition and, respectively, the point of recording the temperature throughout the strip, was different at every scanning velocity.

Table 5. Equations of fitted curves of laser power–temperature simulation results with a laser spot diameter of 80 μm. In equations, T denotes the temperature (K) and P denotes the laser power (W).

Velocity (m/s)	Fitted Curve Equation	Slope	Domain	Range	Error (%)
$0.6$	$T=11.17P+1491$	$11.17$	$60\le P\le 160$	$2161\le T\le 3278$	$1.35$
$0.9$	$T=10.18P+1227$	$10.18$	$60\le P\le 190$	$1837\le T\le 3161$	$1.56$
$1.2$	$T=7.8P+1160$	$7.8$	$60\le P\le 260$	$1628\le T\le 3188$	$2.16$
$1.4$	$T=7.367P+1094$	$7.36$	$60\le P\le 280$	$1491\le T\le 3111$	$2.96$

shows equations of the fitted curves for laser power–temperature simulation results in which the most important factor is the slope. Referring to Table 5, the slope of the curve increases when the scanning velocity decreases. In fact, the temperature increase rate rises when scanning velocity decreases. The slope of the linear equation may be used as a transfer function in a control system design if a process control is considered for the 3D printer machine. Namely, by using the relationship between temperature and laser power for a given scanning speed and laser spot diameter, the machine could be able to determine a suitable laser power to achieve the desired temperature instantly.

Figure 5 shows the fitted curves of laser power–temperature in various scanning speeds together. The red lines split the graph into three parts. The upper part of the evaporation temperature line denotes laser powers, which will cause evaporation mixing melting and the related defects in part, while the lower part of the melting temperature line will have unmelted or low-melted/sintered powders in the fabricated part. The laser power should be able to melt not only the powders of the new layer, but also it should be able to melt a part of the previous melted layers (lower and neighboring layers) again to bond the new and prior layers together. The proper laser powers for melting are the areas between evaporation and melting temperature lines.

6.2. Effect of Laser Spot Diameter

Figure 6 illustrates the results of the simulations and fitted curves for the effect of the laser spot diameter changes on the temperature of the powder layer at the depth of 40$\mathsf{\mu }\mathrm{m}$. Increasing the melt-pool temperature can be explained via the energy density concept. Energy density is defined as the ratio of laser power to fabrication parameters, one of which is the laser spot diameter. The smaller the spot diameter, the higher the energy density and melt-pool temperature.

Referring to Equations (2) and (3), the second-order relation of the laser spot diameter to the heat source could be described. The Gaussian distribution of the heat source for several laser spot diameters is shown in Figure 7. During constant laser power, the effect of different laser spot diameters on the heat source is evident. As discussed earlier, temperature values have been recorded in the same conditions.

Table 6. Equations of fitted curves of laser spot diameter–temperature simulation results with a laser power of 150 W. In equations, T denotes the temperature (K) and d denotes the laser spot diameter (μm).

Velocity (m/s)	Fitted Curve Equation	Domain	Range	Error (%)
$0.6$	$\mathrm{T}=0.01945{\mathrm{d}}^2-15.29\mathrm{d}+4491$	$100\le \mathrm{d}\le 310$	$1620\le \mathrm{T}\le 3156$	$1.365$
$0.9$	$\mathrm{T}=0.04837{\mathrm{d}}^2-21.29\mathrm{d}+3999$	$40\le \mathrm{d}\le 210$	$1661\le \mathrm{T}\le 3224$	$1.52$
$1.2$	$\mathrm{T}=0.0482{\mathrm{d}}^2-21.33\mathrm{d}+3803$	$40\le \mathrm{d}\le 170$	$1569\le \mathrm{T}\le 3026$	$1.98$
$1.4$	$\mathrm{T}=0.0398{\mathrm{d}}^2-18.9\mathrm{d}+3576$	$40\le \mathrm{d}\le 170$	$1513\le \mathrm{T}\le 2883$	$1.57$

denotes the equations of the second-order fitted curves of the laser spot diameter–temperature curves.

In Figure 8, the red lines split the graph into three parts. It illustrates the fitted curves of the laser spot diameter–temperature relationship. The diameter values whose relative temperatures are under the melting line will not have sufficient capability to melt the stainless-steel powder completely. However, those diameters whose relative temperatures are above the evaporation line will result in evaporation mixing with melting under the defined situation of the laser power, scanning velocity, and laser spot diameter. The temperature below the melting line will lead to defects such as not melting of powders, district melting, and weak or lack of bonding between layers of printing. On the other hand, temperatures exceeding evaporation temperature line will lead to defects such as spatters, holes, overcooking, and high heat tensions. Suitable diameters for fabrication are the diameters in the middle part of the graph.

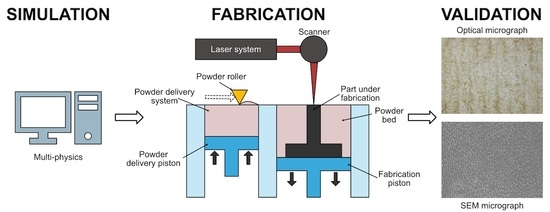
6.3. Experimental Confirmation

Using stainless steel 316L powders, ten samples were manufactured in a Concept Laser M2 Cusing Machine. Samples were fabricated with ten various sets of parameters, which are listed in

Table 7. Parameter sets of fabricated samples. A hatch space of $115\mathsf{\mu }\mathrm{m}$ was used.

Sample	$\mathbf{Laser}\mathbf{Power}\left(\mathbf{W}\right)$	$\mathbf{Laser}\mathbf{Spot}\mathbf{Diameter}\left(\mathsf{\mu }\mathbf{m}\right)$	Scanning Velocity (m/s)
a	$150$	$100$	$0.6$
b	$150$	$40$	$0.9$
c	$150$	$130$	$0.6$
d	$150$	$80$	$0.9$
e	$150$	$110$	$0.9$
f	$150$	$160$	$0.6$
g	$150$	$160$	$1.2$
h	$130$	$80$	$0.6$
i	$110$	$80$	0.6
j	$80$	$80$	$1.4$

. Scanning velocities of 0.6 m/s, $0.9\mathrm{m}/\mathrm{s}$, $1.2\mathrm{m}/\mathrm{s}$, and $1.4\mathrm{m}/\mathrm{s}$ were used during the experimental study. Fabricated samples were categorized into two groups of constant laser spot diameter and constant laser power (for more details, please see the Supplementary Materials). Based on the simulation results obtained from the multiphysics software Comsol, three regions were specified which are: “below melting temperature line”, “between melting temperature and evaporation temperature lines”, and “above the evaporation temperature line”. The emphasis was given to the region that offers defectless and usable structures, which is “between melting and evaporation temperature lines”. This rich area shows the variety of parameters presented by the research. In addition, samples were fabricated employing parameters from sensitive areas with a potential of lack of fusion, “below melting temperature line”, and over melting, “above the evaporation temperature line”, to show the kind of results obtained by selecting parameters from these sensitive areas. Microstructures were examined and results with respect to the selected parameters were obtained.

Referring to optic micrographs of the fabricated samples in Figure 9, defects are seen in samples (a), (b), (g), and (j). Voids in samples (a) and (b) are mainly circular. Defects in the samples (g) and (j), are large irregular defects that are the result of lack of fusion and not having sufficient energy in melting. The large irregular defects indicate insufficient layer–layer or track–track bonding [38]. These defects spread unevenly in the 20–250 $\mathsf{\mu }\mathrm{m}$ length range in cases (g) and (j) in Figure 9. There are some defects in the sample (e), which may not be, in general, related to parameter selection. They could be related to the inert gas trapped in the powder production process, powder bed packing or equipment-related defects such as the deflection of the beam and the calibration error of beam and also insufficiently qualified Galvano mirrors [41].

As cases (a) and (b) show in Figure 9, extreme laser power triggers various defects. Powder denudation is one of them, which causes large and grooved defects. Another defect could be spatter that occurs with high energy inputs, and details are provided in the Figure 9. Spatter occurs when the metal vapor force overcomes the surface tension force and it is difficult to be melted in the next layers; usually spatters are larger than powder size, and would remain as inclusions [42]. Keyholes are one of the most common defects with high energy inputs, which are a result of the vaporization of metal [38]. In cases (a) and (b) of Figure 9, the defects are generally in the 35–55$\mathsf{\mu }\mathrm{m}$ range and are typically larger than the powder size. At high energies, crack defects are another defect that is related to high-temperature gradients. Excessive energy input increases cracking ability by decreasing the cracking stress threshold (see Supplementary Materials) [38]. Two spatters with a total length of close to 100 μm are shown in Figure 9 as a result of excessive energy implementation in sample (a). A crack about 50 μm long caused by the same factor in sample (b) is shown in Figure 9; also, voids could be observed with a diameter of 30–50 $\mathsf{\mu }\mathrm{m}$ with an interlayered morphology. The lines are related to the melt-pool boundaries, and they possibly are the result of high residual stress in the high-speed cooling process. It could encourage the formation of the crack along melt-pool boundaries (Figure 10) [43].

Unmelted regions that belong to the sample j are shown more accurately in Figure 10. Unmelted powders are evident, and those pores could have two causes. One of them is the lack of sufficient energy to melt them, and another reason is the balling. The balling is the agglomeration of powders to minimize the surface energy due to high viscosity or high wetting angle of the molten track [43]. Regarding the selected parameter set for the fabrication of sample j and Figure 10, in this case, the reason for the phenomena is insufficient laser energy to melt powders.

There are some other defects which may not depend on the parameters of fabrication, and could probably occur during any fabrication parameters. One of them is gas bubbles, which are entrapped in the melt. Another common defect is due to reusing powder from the previous fabrications [38,43,44,45,46,47,48,49,50,51].

The samples of (c), (d), (e), (f), (h), and (i) have minimum defects and are almost clean. These samples have parameter sets located in the area between the melting and evaporation lines in the diagram of the simulation results. Their SEM images show favorable structures (see Supplementary Materials, Figures S3 and S4). Reflection of SEM images of experimental results on simulation results is shown more conveniently in Supplementary Materials.

It is also important to note that the melt-pool lifetime, the duration in which the powder melts and eventually solidifies, is a determinative factor in the melting process. Insufficient lifetime could result in incomplete melting and insufficient wetting of neighboring powders. It hinders the melting phase to propagate. Consequently, this inability will weaken melting the powders to ensure the stable and continuous melt-pool and satisfy hatch space. Sample (g) could be an example of this phenomena. Although the relative temperature for the parameter set of this sample is approximately on the melting temperature line, nevertheless there are unmelted powders in its microstructure. Based on the few previous sentences, most likely, these unmelted powders are a result of an insufficient lifetime ($47 \mathsf{\mu }\mathrm{s}$ based on the simulation for sample (g) of the melt-pool). Due to this issue, the area near the melting temperature line is a delicate area for the process fluctuations and therefore should be avoided for a guaranteed result.

Appearance of the lack of fusion defects in samples (g) and (j) with energy densities of $19 \mathrm{J}/{\mathrm{mm}}^3$ and $18 \mathrm{J}/{\mathrm{mm}}^3$ and relevant temperatures near to the melting point, reveals that process parameters should be selected outside of this insecure area. Process parameters that result in a temperature of more than almost $2000 \mathrm{K}$ and an energy density above $35 \mathrm{J}/{\mathrm{mm}}^3$, and also do not exceed the evaporation temperature, will be safe and will allow adequate melt-pool temperature, life-time duration and, as a result, a high-density final product.

Compared with the energy densities reported for producing stainless steel 316L in the literature, in which Yusuf, Shahir Mohd, et al. [52] reported $42 \mathrm{J}/{\mathrm{mm}}^3$, Kamath, Spierings, Adriaan B., and Gideon Levy [53] reported $33 \mathrm{J}/{\mathrm{mm}}^3$, and Li, Ruidi, et al. [54] reported $42 \mathrm{J}/{\mathrm{mm}}^3$, the abovementioned milestones show acceptable conformity.

Additionally, the corresponding energy density to the standard parameter set that the Concept Laser company has given for the machine employed for the experimental study here is $42.9 \mathrm{J}/{\mathrm{mm}}^3$.

7. Conclusions

The developed model and the formulated mathematical relationships between laser power, laser spot diameter, and temperature are a powerful tool to calculate melt-pool temperature and to predict its behavior. The model can predict process parameters by simulating the formed temperature during the process. The mathematical expressions could also be used to control melt-pool temperature. The mathematical relationships between parameters are used to give an overview of the laser-powder interaction, which reduces the need to simulate for each set of parameters. These equations could also be potentially used to overcome the challenge of experimental testing for each set of parameters to obtain the appropriate sets of parameters for production.

For 316L stainless steel powder, temperatures at 40 $\mathsf{\mu }\mathrm{m}$ depth of the layer were obtained for various laser powers, scanning velocities, and laser spot diameters. The simulation results were fitted on the curves, and the equations (mathematical relationships between process parameters) of the fitted curves were obtained. One of the most important pieces of data in laser power–temperature equations is the slope of the equations. The slopes could be considered as transfer functions in a control system. Therefore, a controller design could be performed, and the process may be controlled with a temperature or any other available process parameter feedback(s). The feedback system can feed the control system using real-time temperatures measured by a thermal camera.