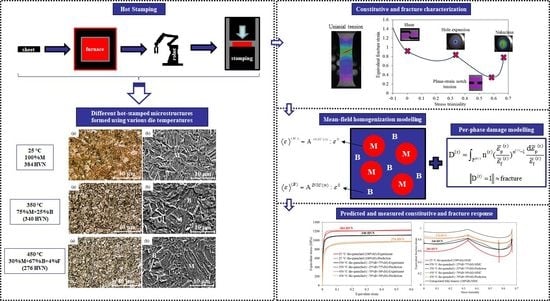
Microstructure-Based Modelling of Flow and Fracture Behavior of Tailored Microstructures of Ductibor^® 1000-AS Steel

Abstract

Emerging grades of press-hardening steels such as Ductibor^® 1000-AS are now commercially available for use within tailor-welded blanks (TWBs) to enhance ductility and energy absorption in hot-stamped automotive structural components. This study examines the constitutive (hardening) response and fracture limits of Ductibor^® 1000-AS as functions of the as-quenched microstructure after hot stamping. Three different microstructures consisting of bainite and martensite were obtained by hot stamping with die temperatures of 25 °C, 350 °C, and 450 °C. Mechanical characterization was performed to determine the hardening curves and plane-stress fracture loci for the different quench conditions (cooling rates). Uniaxial-tension and shear tests were conducted to experimentally capture the hardening response to large strain levels. Shear, conical hole-expansion, plane-strain notch tension, and Nakazima tests were carried out to evaluate the stress-state dependence of fracture. A mean-field homogenization (MFH) scheme was applied to model the constitutive and fracture behavior of the mixed-phase microstructures. A dislocation-based hardening model was adopted for the individual phases, which accounts for material chemistry, inter-phase carbon partitioning, and dislocation evolution. The per-phase fracture modelling was executed using a phenomenological damage index based upon the stress state within each phase. The results revealed that the 25 °C hot-stamped material condition with a fully martensite microstructure exhibited the highest level of strength and the lowest degree of ductility. As bainite was formed in the final microstructure by quenching at higher die temperatures, the strength decreased, while the ductility increased. The predicted constitutive and fracture responses in the hot-stamped microstructures were in line with the measured data. Accordingly, the established numerical strategy was extended to predict the mechanical behavior of Ductibor^® 1000-AS for a broad range of intermediate as-quenched microstructures.

1. Introduction

Boron steels are commonly used in the production of car structures with intrusion-resisting applications [1]. The hot-stamping (press-hardening) process is typically used to form these steels so as to exploit their higher formability at elevated temperatures and strengthening during quenching [2,3]. The resultant high-strength hot-stamped components often have limited ductility and energy-absorption capacity and might not be suitable for crash-safety applications individually [4]. To expand the range of applications of hot stamping, tailor-welded blanks (TWBs) were introduced to fabricate products with various combinations of strength and ductility. The parent metals in such weldments acquire distinct levels of strength and ductility in final press-hardened products due to differences in their hardenability [5].

Usibor^® 1500-AS and Ductibor^® 500-AS, with strength levels of around 1500 MPa and 600 MPa and elongation of 6% and 22% in the die-quenched condition, respectively, are two steels that have been combined within hot-stamping TWBs [6]. Usibor^® 1500-AS attains a fully martensitic microstructure after die quenching [7], whilst the press-hardened Ductibor^® 500-AS microstructure is mostly ferritic-martensitic [8]. Naderi et al. [9], Bardelcik et al. [10], Eller et al. [11], Turetta et al. [12], Barcellona and Palmeri [13], Taylor et al. [14], and Mohr and Ebnoether [15] studied the mechanical response of Usibor^® 1500-AS with various microstructures. Abdollahpoor et al. [16] investigated the sensitivity of the Usibor^® 1500-AS microstructure and hardness to hot-stamping process parameters. Hagenah et al. [17] generated a material model to calculate the Usibor^® 1500-AS tensile strength in different hot-stamped conditions according to the quench rates and plastic strains experienced during the press-hardening process. Srithananan et al. [18], Östlund et al. [19], and Golling et al. [20,21] calculated the flow and fracture behavior of various as-quenched conditions of Usibor^® 1500-AS using microstructure-based models. Mishra [22] reported on the microstructures of Ductibor^® 500-AS under distinct cooling conditions and examined their mechanical properties. Samadian et al. [23] investigated the dependency of the constitutive and fracture behavior of Ductibor^® 500-AS on its as-quenched microstructures.

Ductibor^® 1000-AS is an alternative to Ductibor^® 500-AS in press-hardening TWBs, with strength and ductility that are intermediate between those of Usibor^® 1500-AS and Ductibor^® 500-AS after hot stamping. Similar to Ductibor^® 500-AS, this steel can also be joined to Usibor^® 1500-AS within TWBs to enhance the ductility of press-hardened products, thereby improving their energy absorption. There are relatively few studies on Ductibor^® 1000-AS in the open academic literature. Notable exceptions include Güner et al. [24] and Sarkar et al. [25], who studied the effects of different process parameters such as the austenitization temperature, furnace-to-die transfer time, as well as the die pressure, temperature, and geometry on the final properties of Ductibor^® 1000-AS after hot stamping. In terms of in-service properties, Lee [26] examined the crashworthiness of monolithic Ductibor^® 1000-AS in the die-quenched condition. Mohamadizadeh et al. [27] investigated the spot-weld failure in the die-quenched Ductibor^® 1000-AS.

At present, no published research has focused on the correlation between the microstructure and mechanical properties of the hot-stamped Ductibor^® 1000-AS, while the mechanical performance of press-hardened products is known to vary significantly with microstructural changes due to fluctuations in hot-stamping conditions. Given the crash-safety applications of Ductibor^® 1000-AS and the dependency of its mechanical response on the as-quenched microstructure, it is crucial to understand the interrelationship between the microstructure and mechanical properties of this steel following hot stamping. To address this gap in the literature, the current work examined the hardening and fracture behavior of Ductibor^® 1000-AS in different die-quenched conditions under quasi-static loading. To develop distinct microstructures, the steel blanks were hot-stamped using flat dies kept at temperatures of 25 °C, 350 °C, and 450 °C. Microstructure and hardness investigations were conducted on the as-quenched blanks. Uniaxial-tension, shear, conical hole-expansion, plane-strain notch tension, and Nakazima tests were performed to characterize the mechanical behavior of each material condition (microstructure) in terms of hardening and fracture. A mean-field homogenization (MFH) strategy was developed to model the hardening and fracture responses in the mixed-phase microstructures based on the flow behavior of the micro-constituents calculated using a dislocation-based constitutive model and tracking damage accumulation within each micro-constituent using a phenomenological damage indicator. The predictions and measurements for the produced multi-phase microstructures were then compared. Ultimately, the developed numerical scheme was applied to predict the constitutive and fracture responses in Ductibor^® 1000-AS for a range of the as-quenched microstructures with several phase volume fractions.

2. Experiments

The material of interest in the study was a 1.2 mm-thick Ductibor^® 1000-AS steel sheet, with the nominal elemental composition given in

Table 1. The Ductibor^® 1000-AS chemical composition (unit: wt.%).

C	Mn	Ti	Nb	Cr	Si	P	S	B	Fe
0.081	1.643	0.015	0.055	0.073	0.362	0.011	0.001	0.003	balance

.

Three different microstructures were obtained by austenitization at 930 °C for 390 s (6.5 min) in an air furnace and then quenching between flat dies with temperatures of 25 °C, 350 °C, and 450 °C under a 15 MPa contact pressure for 15 s, followed by air cooling to room temperature. The 25 °C temperature represents an “ideal” die temperature targeted for hot stamping, although hot-stamping die temperatures in practice can increase up to 200 °C during mass production due to inadequate cooling [24]. Ductibor^® 1000-AS, similar to Usibor^® 1500-AS, also has the potential to be used within the in-die heating (IDH) hot-stamping process to create components with graded strength and ductility. The local die temperature in the IDH hot-stamping process can exceed 400 °C [28]; therefore, the selected die temperatures cover the range of expected values within various hot-stamping processes and serve to produce different microstructures. The average heating rate of the blanks was 7 °C/s, and their average cooling rates while cooling from 700 °C to 200 °C were 243 °C/s, 47 °C/s, and 21 °C/s for the 25 °C, 350 °C, and 450 °C die temperatures, respectively. The thermal history measurements were conducted using thermocouples and a data acquisition system of Omega OMB-DAQ-55 (Omega, St-Eustache, QC, Canada). The details about the specimen geometry and thermocouple locations are provided by Omer et al. [29]. Microstructure and hardness investigations were performed for the as-received and as-quenched blanks. Light optical microscopy (LOM) (Keyence, Mississauga, ON, Canada) and scanning electron microscopy (SEM) (FEI, Hillsboro, OR, USA) were used for the microstructural examinations. A 5% nital etchant was used to reveal the microstructures. Analyses of phase quantities were performed on the SEM images (due to higher clarity with respect to the LOM images) using a systematic manual point-count method [30]. Vickers microhardness measurements were carried out under a load of 1 kgf (~9.8 N) for a 15 s dwell time.

To measure the constitutive behavior of each material condition, tensile tests were performed on samples (Figure 1) of the hot-stamped blanks cut at angles of 0°, 45°, and/or 90° relative to the rolling direction (RD). The fracture response along the limiting direction in terms of ductility, i.e., the transverse direction (TD), was characterized through shear, conical hole-expansion, plane-strain notch tension, and Nakazima tests, with the specimen geometries illustrated in Figure 1.

The tensile, shear, and plane-strain notch tension tests were conducted with an initial nominal strain rate of 0.01/s. In the hole-expansion and Nakazima tests, a constant punch speed of 0.25 mm/s and a binder force of 660 kN were applied. To promote a fracture near the sample center in the Nakazima tests, Teflon sheets with petroleum jelly were placed between the punch and specimens. At least four repeats were performed for each experiment type. A stereoscopic digital image correlation (DIC) system with Point Grey Research GRAS-50S5M-C cameras (Point Grey, Richmond, BC, Canada) and the Correlated Solutions DIC software of Vic3D (9, Correlated Solutions, Irmo, SC, USA) were utilized to measure the surface strains of the specimens. In the DIC analyses, a 0.3 mm virtual strain gauge length (VSGL) [36] with a 1 or 2 pixel step size and a 5 filter size was employed. Sandblasting was carried out on the hot-stamped samples prior to testing to remove the Al-Si coating, which would otherwise flake off and compromise the DIC strain measurements. For the tensile tests, the instant of fracture was considered to be the moment prior to material rupture given the rapid occurrence of fracture across the gauge area. For the hole-expansion, plane-strain notch tension, and Nakazima tests, the first visible cracks corresponded to the onset of fracture. Due to the difficulty in the visual determination of crack formation in the shear tests, the point of maximum load was chosen to correspond to the onset of fracture, which is expected to be a conservative estimate [36]. For the tensile samples, axial extensometers with 50 mm lengths were set up in Vic3D to measure engineering strains. For the shear, plane-strain notch tension, and Nakazima specimens, the principal strains at fracture were extracted from rectangle- (0.25 mm × 0.4 mm) and circle-shaped (0.25 mm and 0.5 mm in radius) sampling areas around the fracture locations in Vic3D, respectively. For the hole-expansion samples with the CNC-machined hole edges, the outer diameters of the holes at the initial and final stages of deformation ($d_0$ and $d_f$, respectively) were measured to obtain the equivalent fracture strains (${\epsilon }_f^{eq}$) via Equation (1), given the pure tension stress state that was assumed at the edges of the holes, away from the conical punch.

$${\epsilon }_f^{eq}=\ln \frac{d_f}{d_0}$$

(1)

It is noted that for the plane-strain notch tension and Nakazima specimens, the fracture strains were also measured based on post-mortem thickness measurements (Figure 2) due to localized necking before fracture. The surface-measurement basis of the DIC system normally results in the underestimation of fracture strains for the above-mentioned samples. Nonetheless, the post-mortem thickness measurements are rupture strains and thus generally overestimate the fracture strain that corresponds to the onset of fracture [37]. For the strain corrections, the methodology by Gorji et al. [38] was adopted, whereby deformation is assumed to be plane strain between the last DIC image and rupture. Given von Mises plasticity, the corrected equivalent fracture strains were calculated using Equation (2) in terms of the DIC-based equivalent fracture strains (${\epsilon }_{DIC}^{eq}$), initial thicknesses ($t_0$), thicknesses at fracture ($t_f$), and DIC-based third principal strains at fracture (${\epsilon }_3^{DIC}$) [23]:

$${\epsilon }_f^{eq}={\epsilon }_{DIC}^{eq}-\frac{2}{\sqrt{3}}(\ln \frac{t_f}{t_0}-{\epsilon }_3^{DIC})$$

(2)

3. Microstructure-Based Modelling

To model the constitutive and fracture responses in the bainitic-martensitic microstructures of the die-quenched Ductibor^® 1000-AS, the mean-field homogenization (MFH) approach due to Samadian et al. [39] was extended to consider changes in the strength levels of the constituent phases in different microstructures. A detailed description of the proposed numerical strategy is provided in the following sections.

3.1. Flow Response

The continuum hardening behavior of multi-phase (bainitic-martensitic) microstructures of Ductibor^® 1000-AS in the TD was modelled micromechanically using the interpolative self-consistent (INSC) MFH model developed by Samadian et al. [40]. The mixed-phase microstructures were treated as dual-phase composites, in which the softer bainitic-phase matrix encloses randomly distributed, spherical, harder martensitic-phase inclusions. Strain partitioning between the micro-constituents for any given displacement boundary conditions was computed using the INSC strain concentration tensors for the inclusions and matrix (${\mathrm{A}}^{INSC(i)}$ and ${\mathrm{A}}^{INSC(m)}$, respectively), presented in Equations (3) and (4):

$$\stackrel{{\langle \epsilon \rangle }^{(i)}={\mathrm{A}}^{INSC(i)}:\langle \epsilon \rangle }{\to }\begin{array}{c}\end{array}{\mathrm{A}}^{INSC(i)}=(1-\xi ){\mathrm{A}}^{SC(i)}+\xi {\mathrm{A}}^{ISC(i)}$$

(3)

$$\stackrel{{\langle \epsilon \rangle }^{(m)}={\mathrm{A}}^{INSC(m)}:\langle \epsilon \rangle }{\to }\begin{array}{c}\end{array}{\mathrm{A}}^{INSC(m)}=\frac{{\mathrm{I}}^{(4)}-f_{(i)}{\mathrm{A}}^{INSC(i)}}{f_{(m)}}$$

(4)

in which:

$${\mathrm{A}}^{SC(i)}={[{\mathrm{I}}^{(4)}+\overline{\mathrm{S}}:{[\overline{\mathrm{L}}]}^{-1}:({\mathrm{L}}^{(i)}-\overline{\mathrm{L}})]}^{-1}$$

(5)

$${\mathrm{A}}^{ISC(m)}={[{\mathrm{I}}^{(4)}+\overline{\mathrm{S}}:{[\overline{\mathrm{L}}]}^{-1}:({\mathrm{L}}^{(m)}-\overline{\mathrm{L}})]}^{-1}\stackrel{}{\to }\begin{array}{c}\end{array}{\mathrm{A}}^{ISC(i)}=\frac{{\mathrm{I}}^{(4)}-f_{(m)}{\mathrm{A}}^{ISC(m)}}{f_{(i)}}$$

(6)

In the above equations, ${\langle \epsilon \rangle }^{(i)}$ and ${\langle \epsilon \rangle }^{(m)}$ are strain tensors for the inclusions and matrix; $\langle \epsilon \rangle$ is the macroscopic strain tensor; ${\mathrm{A}}^{SC(i)}$ is the self-consistent (SC) strain concentration tensor for the inclusions; ${\mathrm{A}}^{ISC(i)}$ and ${\mathrm{A}}^{ISC(m)}$ are the inverse self-consistent (ISC) strain concentration tensors for the inclusions and matrix; ${\mathrm{I}}^{(4)}$ and $\xi$ are the fourth-order identity tensor and an interpolation function; $f_{(i)}$ and $f_{(m)}$ are the volume fractions of the inclusions and matrix; ${\mathrm{L}}^{(i)}$, ${\mathrm{L}}^{(m)}$, and $\overline{\mathrm{L}}$ are the inclusion, matrix, and composite fourth-order elastic tensors; and $\overline{\mathrm{S}}$ is the fourth-order Eshelby tensor based upon the properties of the composite and the geometry of inclusions, respectively. The interpolation function by Lielens et al. [41] was applied in the INSC model:

$$\xi =\frac{1}{2}{f}_{(i)}(1+f_{(i)})$$

(7)

In Equations (5) and (6), since the mechanical properties of the composite (steel) are not known in advance, $\overline{\mathrm{L}}$ and $\overline{\mathrm{S}}$ are computed iteratively within the MFH integration for each step of deformation. It should be noted that the INSC model, which is an interpolation of the SC and ISC schemes, is able to consider the influences of the inclusion volume fractions and self-interactions. The first-order secant-based linearization scheme was used to enable the MFH model to describe the non-linear hardening behavior of the material [42]. This linearization scheme updates stresses and strains in the micro-constituents via their secant moduli (ratios of overall stress and strain in the micro-constituents) and can only be used in proportionally monotonic loading.

The per-phase flow behavior was modelled using the hardening law due to Rodriguez and Gutierrez [43]:

$$\sigma (\mathrm{MPa})={\sigma }_0+\Delta \sigma +\alpha M\mu \sqrt{b}\sqrt{\frac{1-\exp (-Mk{\overline{\epsilon }}^p)}{kL}}$$

(8)

where:

$${\sigma }_0=77+750(\%P)+60(\%Si)+80(\%Cu)+45(\%Ni)+60(\%Cr)+11(\%Mo)+5000(\%N_{ss})$$

(9)

for bainite (adopted from [18]):

$$\Delta \sigma =900(\%C_{ss}^B)$$

(10)

for martensite:

$$\Delta \sigma =3065(\%C_{ss}^M)-161$$

(11)

This model takes account of the lattice friction (Peierls stress) and alloying elements by ${\sigma }_0$, inter-phase carbon partitioning by $\Delta \sigma$, and dislocation evolution with plastic deformation by the last expression in Equation (8). In this study, the intra-phase contents of all alloying elements but carbon were assumed to be the same as the macroscopic chemistry. The carbon concentration of martensite was considered to be a calibration parameter for the studied mixed-phase microstructures. Accordingly, the carbon content of bainite was calculated using Equation (12) in terms of the carbon weight percentages within the steel and martensite ($\%C_{ss}^{steel}$ and $\%C_M$, respectively) and the martensite volume fraction ($V_M$), given the carbon weight balance in the steel:

$$\%C_B=\frac{\%C_{steel}-V_M.\%C_M}{1-V_M}$$

(12)

A dislocation strengthening constant ($\alpha$) of 0.33, Taylor’s factor ($M$) of 3, a shear modulus ($\mu$) of 80,000 MPa, and a Burgers vector ($b$) of 2.5 × 10⁻¹⁰ m were considered [44]. The martensite dislocation mean free path ($L$) and recovery rate ($k$) were obtained by the calibration of the hardening model in Equation (8) with the experimental hardening response of the fully martensitic microstructure. For the bainite, $L$ and $k$ were identified by a least-squares minimization of the deviation of the predicted flow stress-strain data with respect to the tensile and shear-based experimental results.

The mixed-phase microstructures and the constituent phases were assumed to be isotropic and adhere to von Mises plasticity. The stresses within the micro-constituents, corresponding to the partitioned strains calculated by the INSC model, were obtained via the convex cutting-plane (CCP) algorithm [45]. A constraint of plane-stress loading was imposed at the macroscopic level based on the Newton iteration scheme [45]:

$${(\Delta {\epsilon }_{33})}_{\mathrm{k}}={(\Delta {\epsilon }_{33})}_{\mathrm{k}-1}-{\left[\frac{{\sigma }_{33}}{{\overline{\mathrm{L}}}_{3333}}\right]}_{\mathrm{k}-1}\begin{array}{ccc}& & (\mathrm{k}=1,2,\dots ,\&\begin{array}{c}\mathrm{n}\end{array})\end{array}$$

(13)

In this technique, through-thickness stress components (${\sigma }_{33}$) at different steps of deformation were enforced to be within a given tolerance ($\left|{\sigma }_{33}\right|\le {10}^{-4}$ MPa) by varying the respective strain-increment components ($\Delta {\epsilon }_{33}$) in distinct iterations ($\mathrm{k}$).

3.1.1. Flow Curves of Reference Microstructures

The true stress-strain response of the developed microstructures of Ductibor^® 1000-AS was first calculated up to the ultimate tensile strength (UTS) based on the engineering stress-strain data acquired in the tensile tests along the TD. The obtained flow stresses and strains were then extrapolated beyond the UTS points using the shear-test data based on the shear-conversion technique due to Rahmaan et al. [36]. In this method, the lack of localized necking up to very large strains in the shear specimens is exploited, and shear stresses and strains are converted to tensile values using the shear-to-tensile stress ratio and plastic-work equivalence. In this work, as per a suggestion by Noder and Butcher [46], the stress ratios at the diffuse-necking (UTS) points were adopted for converting the shear stresses (until the peak shear stress) to the tensile stresses beyond the UTS points. The work-conjugate equivalent plastic strains (${\epsilon }_{eq}^p$) were then computed using Equation (14) [47], considering the deviation of stress and strain principal axes from each other during simple-shear loading:

$${\epsilon }_{eq}^p=2\left(\frac{\tau }{{\sigma }_n}\right)\mathit{sinh}\left({\epsilon }_1^p\right)$$

(14)

In the above equation, $\tau$ and ${\sigma }_n$ are the shear stress and tensile (normal) stresses, and ${\epsilon }_1^p$ is the major principal plastic strain in the shear testing.

3.2. Fracture Response

To model fracture in the Ductibor^® 1000-AS mixed-phase (bainitic-martensitic) microstructures, the Generalized Incremental Stress State Dependent Damage Model (GISSMO) [48] was employed within the MFH numerical framework to compute the accumulation of damage at the micro level. In this manner, the GISSMO damage indicator for the individual phases ($D^{(r)}$) was calculated using Equation (15) based on their instantaneous equivalent plastic strain (${\overline{\epsilon }}_p{}^{(r)}$) and equivalent fracture strain associated with their current stress states (${\overline{\epsilon }}_f{}^{(r)}$) at each deformation level.

$$D^{(r)}={\displaystyle \int d{D}^{(r)}}={\displaystyle \int d\begin{array}{r}\hfill [{(\frac{{\overline{\epsilon }}_p{}^{(r)}}{{\overline{\epsilon }}_f{}^{(r)}})}^{n^{(r)}}]\end{array}}={\displaystyle {\int }_{{\overline{\epsilon }}^p{}^{(r)}}\frac{n^{(r)}}{{\overline{\epsilon }}_f{}^{(r)}}{(\frac{{\overline{\epsilon }}_p{}^{(r)}}{{\overline{\epsilon }}_f{}^{(r)}})}^{n^{(r)}-1}d{\overline{\epsilon }}_p{}^{(r)}}$$

(15)

The fracture limits of bainite and martensite were taken from the fracture loci for the Ductibor^® 1000-AS fully bainitic and fully martensitic microstructures, respectively, given the stress triaxiality ($\eta$) and Lode parameters ($\xi$) calculated for each phase using Equations (16) and (17):

$$\eta =\frac{{\sigma }_m}{\overline{\sigma }}$$

(16)

$$\xi =\frac{27}{2}\frac{J_3}{{\overline{\sigma }}^3}$$

(17)

In the above equations, ${\sigma }_m$, $J_3$, and $\overline{\sigma }$ represent the hydrostatic stress, deviatoric stress tensor third invariant, and von Mises equivalent stress, respectively. Given the unknown influence of changes in the micro-scale strength with the phase quantity on the per-phase damage accumulation within the Ductibor^® 1000-AS bainitic-martensitic microstructures, the GISSMO damage exponent for each micro-constituent ($n^{(r)}$) was considered to be a calibration parameter. The optimized values of $n^{(r)}$ were determined using a least-squares technique in FORTRAN 90, minimizing the deviation of the predicted fracture strains from the experimental values. The initiation of fracture in the bainitic-martensitic microstructures corresponded to the moment that the GISSMO damage indicator became unity for either bainite or martensite.

The numerical strategy outlined in Section 3.1 and Section 3.2 was written in the format of a FORTRAN 90 code. Then the constitutive and fracture responses in the Ductibor^® 1000-AS bainitic-martensitic microstructures with a variety of micro-constituent contents were calculated under different loading conditions. The algorithm of the employed scheme for MFH integration is described in [23].

Fracture Loci of Reference Microstructures

The Modified-Mohr-Coulomb (MMC) fracture function (Equation (18)) [49] was used to describe the fracture loci of the hot-stamped microstructures.

$${\overline{\epsilon }}_f={\left[A\cos (\frac{\overline{\theta }\pi }{6})+B(\eta +\frac{1}{3}\sin (\frac{\overline{\theta }\pi }{6}))\right]}^{\begin{array}{c}C\end{array}}$$

(18)

The material parameters of this model ($A$, $B$, and $C$) were calibrated for the individual microstructures based on the respective experimental fracture strains (${\overline{\epsilon }}_f$) and stress states, as described by the stress triaxiality ($\eta$) and normalized Lode angle ($\overline{\theta }$). Given a plane-stress condition, the average stress triaxiality and normalized Lode angle for each fracture test were obtained by Equations (19) and (20) in terms of the ratio of the minor-to-major principal strain increment ($\rho =d{\epsilon }_2/d{\epsilon }_1$) averaged over the measured strain paths until the fracture points.

$$\eta =\frac{\alpha +1}{3\sqrt{{\alpha }^2-\alpha +1}}\begin{array}{r}\hfill \end{array}\to \begin{array}{c}\begin{array}{c}\end{array}\alpha =\frac{{\sigma }_2}{{\sigma }_1}=\frac{2\rho +1}{\rho +2}\end{array}$$

(19)

$$\overline{\theta }=1-\frac{2}{\pi }arc\cos (-\frac{27}{2}\eta ({\eta }^2-\frac{1}{3}))$$

(20)

The calibration operations were carried out based on a least-squares method using a generalized reduced gradient (GRG) algorithm [50].

4. Results and Discussion

4.1. Microstructures and Hardness

Figure 3, Figure 4, Figure 5 and Figure 6 show LOM and SEM images from the as-received and die-quenched microstructures. The phase-quantity and hardness measurements are also presented in

Table 2. The measured hardness and micro-constituent volume fractions (%v) for the studied microstructures of Ductibor^® 1000-AS.

Material Condition	F (%v)	B (%v)	M (%v)	Hardness (HVN)
As-received	88.0 ± 2.1 *	-	12.0 ± 2.1	226 ± 2
25 °C die-quenched	-	-	100	384 ± 4
350 °C die-quenched	-	24.9 ± 3.4	75.1 ± 3.4	340 ± 5
450 °C die-quenched	3.0 ± 0.4	67.4 ± 5.3	29.6 ± 5.5	276 ± 10

* The variations denote the standard deviation.

. The as-received microstructure (Figure 3) comprised a ferritic matrix (the brighter phase in the LOM image and the darker phase in the SEM image) with around 12%v of scattered martensite islands. The mostly ferritic microstructure of this material condition resulted in a relatively low measured hardness of 226 HVN. Following hot stamping, the 25 °C die-quenched (fully quenched) condition exhibited a fully martensitic (100%M) microstructure (Figure 4) with a hardness value of 384 HVN. The lath-type martensite existing in this microstructure shows some degree of auto-tempered morphology. Given the low carbon content of Ductibor^® 1000-AS (0.081 wt.%) and, as a result, its high austenite-to-martensite transformation start temperature ($M_s$ = 451 °C, calculated by Andrew’s model in Equation (21) [51]), the martensite auto-tempering phenomenon [52,53] was not unexpected for this steel.

$$M_s=539-423C-7.5Si-30.4Mn-17.7Ni-12.1Cr-7.5Mo+10Co$$

(21)

The increase in the die temperature to 350 °C and 450 °C led to the decreased martensite volume fractions and the transformation of austenite to the softer phases within the microstructure, thereby reducing the overall hardness. The 350 °C die-quenched condition revealed a ~25% bainitic + ~75% martensitic microstructure (Figure 5) with a hardness value of 340 HVN, while the microstructure of the 450 °C die-quenched condition (Figure 6) comprised around 3% ferrite, 67% bainite, and 30% martensite and had a hardness value of 276 HVN. The measured reductions in the martensite volume fraction and hardness value are due to the decrease in the cooling rate of the blanks (from 243 °C/s to 21 °C/s) with the increase in the temperature of the quenching die (from 25 °C to 450 °C).

4.2. Measured Constitutive Behavior

Figure 7 displays the measured stress-strain response along the TD for different hot-stamped conditions in the tensile and shear tests.

Table 3. The measured tensile properties for different Ductibor^® 1000-AS die-quenched conditions.

Material Condition	UTS (MPa)	Uniform Elongation (%)	Elongation to Fracture (%)
25 °C die-quenched	1122 ± 9 *	4.3 ± 0.1	7.0 ± 0.4
350 °C die-quenched	1009 ± 9	3.9 ± 0.1	7.1 ± 0.2
450 °C die-quenched	833 ± 13	6.1 ± 0.4	10.8 ± 0.6

* The variations denote the standard deviation.

presents a summary of the acquired tensile properties. It can be seen that the 25 °C die-quenched condition revealed the highest strength level and lowest elongation to fracture in both tests, followed by the 350 °C and 450 °C die-quenched conditions, respectively. These trends stem from the increased contents of martensite (the harder phase) within the as-quenched microstructures with the decreased die temperatures (See Table 2). The 450 °C die-quenched condition exhibited the highest uniform elongation due to its higher bainite volume fraction. However, the 25 °C die-quenched condition with a harder microstructure revealed a slightly higher uniform elongation than the 350 °C die-quenched condition. This behavior is correlated with a higher work-hardening rate of the fully quenched condition by virtue of its martensitic microstructure.

As detailed in Section 3.1.1, the shear-conversion technique was employed to extend the tensile flow data for the three hot-stamped conditions to larger strains using the shear-test results. The calculated ratios of shear and tensile stresses vs. plastic work up to the UTS points are displayed in Figure 8a, and the extrapolated flow curves are shown in Figure 8b. It is evident that the stress ratios become almost constant after the initial transients around the material yielding. The stress ratio is then assumed to remain constant at larger strain levels. The shear-to-tensile stress ratios at UTS, adopted for converting the post-UTS shear stresses to the corresponding tensile stresses, were 0.590, 0.579, and 0.588 for the 25 °C, 350 °C, and 450 °C die-quenched conditions, respectively. The converted shear data exhibits a smooth transition from the equivalent plastic strains that correspond to the UTS points to the equivalent plastic strains that are approximately 20 times higher.

For comparison purposes, the hardening curve acquired for the fully quenched Ductibor^® 1000-AS is compared with the flow curves of two common hot-stamping steels of Ductibor^® 500-AS and Usibor^® 1500-AS in the cold die-quenched condition in Figure 9. As can be seen, both Ductibor^® 500-AS and Ductibor^® 1000-AS are weaker than Usibor^® 1500-AS. The higher strength level of Ductibor^® 1000-AS with respect to Ductibor^® 500-AS makes Ductibor^® 1000-AS an attractive alloy to combine with Usibor^® 1500-AS in hot-stamped TWB components.

It is noted that the influence of anisotropy in the material hardening response and the accuracy of the measured tensile-plus-converted shear data were also evaluated in this study, with the results documented within Appendix A and Appendix B as supplemental information.

4.3. Fracture Behavior

Figure 10 shows the distributions of the major principal strain on surfaces of a range of fracture-test specimens of different hot-stamped conditions at one frame prior to fracture. For all cases, it can be seen that deformation was localized within the central regions of the samples. As the distance from the center increases, the material straining decreases.

Figure 11 displays the strain paths, together with the DIC and thickness measurement-based fracture points, obtained at the fracture locations of samples of the three hot-stamped conditions during different fracture experiments. The corresponding averaged stress triaxiality ($\eta$), Lode parameters ($\xi$), and strain ratios ($\rho$) are listed in

Table 4. The averaged stress triaxiality ($\eta$ ), Lode parameters ($\xi$ ), and strain ratios ($\rho$ ) at the fracture locations of fracture-test samples of various die-quenched conditions of Ductibor^® 1000-AS.

Material Condition	Shear	Hole Expansion	Plane-Strain Notch Tension	Nakazima
25 °C die-quenched	$\begin{array}{l}\eta =0\\ \xi =0\\ \rho =-1\end{array}$	$\begin{array}{l}\eta =0.333\\ \xi =1\\ \rho =-0.5\end{array}$	$\begin{array}{l}\eta =0.568\\ \xi =0.084\\ \rho =-0.032\end{array}$	$\begin{array}{l}\eta =0.666\\ \xi =-0.995\\ \rho =0.887\end{array}$
350 °C die-quenched	$\begin{array}{l}\eta =0\\ \xi =0\\ \rho =-1\end{array}$	$\begin{array}{l}\eta =0.333\\ \xi =1\\ \rho =-0.5\end{array}$	$\begin{array}{l}\eta =0.566\\ \xi =0.098\\ \rho =-0.037\end{array}$	$\begin{array}{l}\eta =0.661\\ \xi =-0.919\\ \rho =0.618\end{array}$
450 °C die-quenched	$\begin{array}{l}\eta =0\\ \xi =0\\ \rho =-1\end{array}$	$\begin{array}{l}\eta =0.333\\ \xi =1\\ \rho =-0.5\end{array}$	$\begin{array}{l}\eta =0.564\\ \xi =0.118\\ \rho =-0.045\end{array}$	$\begin{array}{l}\eta =0.665\\ \xi =-0.981\\ \rho =0.796\end{array}$

. The trends of the measured strain paths for each test type are similar in different material conditions. In general, the 25 °C die-quenched samples underwent the lowest strains prior to fracture, followed by the 350 °C and 450 °C die-quenched specimens, respectively. Such discrepancies are consistent with the microstructure and hardness data since material conditions with higher martensite and hardness normally exhibit lower ductility. The DIC-based fracture strains compared to the thickness measurement-based ones have lower values for the plane-strain notch tension and Nakazima tests. This difference reflects the deficiency of the DIC techniques in the measurement of through-thickness straining within the localized necks formed during these tests before fracture.

Figure 12 presents the von Mises equivalent fracture strains of the three hot-stamped conditions for each test. The hardest material condition (25 °C die-quenched), with its fully martensitic microstructure, had the lowest equivalent fracture strains, whilst the intermediate and softest material conditions (350 °C and 450 °C die-quenched, respectively), with a lower martensite content, revealed the higher equivalent fracture strains. As expected, the DIC-based equivalent fracture strains in the plane-strain notch tension and Nakazima tests are lower than the rupture strains from post-mortem thickness measurements. It is noted that the evaluation of the fracture strain in plane-strain tension loading can be impacted by the specimen geometry, test type, and thickness of press-hardening steels. For example, the fracture strains for plane-strain notch tension tests may differ from those obtained in VDA 238–100 V-bend tests [54], whereby fracture is initiated at the surface rather than within the thickness plane. Sarkar et al. [25] reported an equivalent fracture strain in excess of 0.6 in the V-bend testing of a 1.5 mm-thick fully quenched and paint-baked Ductibor^® 1000-AS sheet. The lower equivalent fracture strain measured for this loading condition in the current work (0.47) may also be due to the lack of the paint-baking treatment and lower thickness (1.2 mm) compared to the case in the work by Sarkar et al. [25].

Figure 13a shows fracture loci for each of the three hot-stamped conditions, interpolated using the MMC fracture function (Equation (18)) based on the measured equivalent fracture strains (Figure 12) and stress-state parameters (Table 4) from the fracture tests. The calibrated MMC material parameters for each material condition are given in

Table 5. The MMC material parameters calibrated for various die-quenched conditions of Ductibor^® 1000-AS.

Material Condition	$\mathit{A}$	$\mathit{B}$	$\mathit{C}$
25 °C die-quenched	1.1742	0.1196	−3.1888
350 °C die-quenched	1.1735	0.1883	−1.8950
450 °C die-quenched	1.1573	0.2042	−1.2428

. It is noted that in the calibration process, the equivalent fracture strains obtained by the thickness measurements in the plane-strain notch tension and Nakazima tests were utilized. As expected based on the microstructure and hardness-test results, the 25 °C die-quenched condition with the hardest and most martensitic microstructure revealed the lowest degree of ductility in all of the stress states, while the 350 °C and 450 °C die-quenched conditions with the lower hardness and martensite exhibited the intermediate and highest ductility, respectively. For comparative purposes, the Ductibor^® 1000-AS fracture locus is compared to the fracture loci of two other common hot-stamping steels, Ductibor^® 500-AS and Usibor^® 1500-AS [55], in the cold die-quenched condition in Figure 13b. It is evident that the ductility of Ductibor^® 1000-AS is intermediate to that of Ductibor^® 500-AS and Usibor^® 1500-AS. The higher fracture limits of both Ductibor^® steels make them suitable candidates for joining to Usibor^® 1500-AS in hot-stamping TWBs for use in energy-absorbing components of automobiles.

4.4. MFH Predictions

This section presents the predictions of the established microstructure-based modelling technique for the constitutive and fracture response in Ductibor^® 1000-AS with multi-phase microstructures. It should be noted that in the numerical analyses, the small amount of ferrite (3%) in the 450 °C die-quenched microstructure (Table 2) was assumed to be bainite for simplicity due to the closer mechanical properties of ferrite to bainite as compared to martensite. Therefore, the reference microstructures of the 25 °C, 350 °C, and 450 °C die-quenched conditions in the modelling work were 100% martensitic (100%M), ~25% bainitic plus ~75% martensitic (~25%B + 75%M), and ~70% bainitic plus ~30% martensitic (~70%B + 30%M), respectively.

4.4.1. Predicted Flow Response

The calculated hardening curves for micro-constituents of the three hot-stamped microstructures based on Rodriguez and Gutierrez’s model (Equation (8) [43]) are illustrated in Figure 14. The optimized values of carbon concentrations as well as dislocation mean free paths and recovery rates for the constituent phases are listed in

Table 6. The carbon concentrations of the bainitic and martensitic phases in various material conditions/microstructures of Ductibor^® 1000-AS.

Material Condition/Microstructure	Carbon in Bainite (wt.%)	Carbon in Martensite (wt.%)
25 °C die-quenched (100%M)	-	0.081 ≈ total steel carbon
350 °C die-quenched (~25%B + 75%M)	0.063 (from Equation (12))	0.087 (from calibration)
450 °C die-quenched (~70%B + 30%M)	0.035 (from Equation (12))	0.189 (from calibration)
Fully bainitic (100%B)	0.081 ≈ total steel carbon	-

and

Table 7. The calibrated values of dislocation mean free paths and recovery rates for bainite and martensite in the as-quenched microstructures of Ductibor^® 1000-AS used in Rodriguez and Gutierrez’s model (Equation (8) [43]).

Micro-Constituent	Dislocation Mean Free Path (m)	Recovery Rate
Bainite	1.80 × 10−6	4.30
Martensite	4.40 × 10−8	45.73

, respectively. Figure 14a indicates that martensite had the lowest strength level in the 25 °C die-quenched condition with a fully martensitic microstructure. As the die temperature increased (or the martensite content decreased), the martensitic phase strengthened. This behavior is due to the lower solubility of carbon in bainite, which results in an increased carbon concentration of martensite as the bainite volume fraction increases at higher quenching-die temperatures (See Table 6). Such predictions are consistent with the study by Young and Bhadeshia [56] on the strength of bainitic-martensitic microstructures. They elucidated that as the volume fraction of the bainitic phase increases, more carbon is rejected into the remaining austenite, and as a result, martensite with a higher carbon concentration is transformed from the austenitic phase. A comparison of the predicted hardening response for bainite in the reference mixed-phase microstructures and a fully bainitic (100%B) microstructure of Ductibor^® 1000-AS (Figure 14b) reveals that the bainitic micro-constituent had the highest strength level when it was the only phase in the microstructure (i.e., 100%B). The reason is that bainite in a fully bainitic microstructure had the highest carbon content (equal to the total amount of carbon in the steel), while its carbon concentration dropped within the bainitic-martensitic microstructures. Seol et al. [57], Clarke et al. [58], and Timokhina et al. [59] also reported lower amounts of carbon in the bainitic phase of bainitic-austenitic (potentially martensitic) microstructures of low and high carbon steels, as compared to the overall carbon content in the steel. Bainite in the 350 °C die-quenched microstructure was predicted to have a higher carbon content and, as a result, higher strength than that in the 450 °C die-quenched microstructure. Such a prediction is in line with the observations by Bhadeshia and Christian [60], who demonstrated that bainite formed at lower temperatures has higher carbon.

It is noted that the calibrated dislocation mean free paths and recovery rates for bainite and martensite (Table 7) have values on the same order of magnitude as those reported in the literature. For example, Rodrigues and Gutierrez [43] reported dislocation mean free paths and recovery rates of 1.6–2.4 µm and 2.3–13 for bainite and 0.035–0.045 µm and 37.8–43.8 for martensite in C-Mn steels, respectively. Ramazani et al. [44,61] applied dislocation mean free paths of 0.2 µm and 0.038 µm and recovery rates of 0.83 and 41 for bainite and martensite in dual-phase steels, respectively. The lower dislocation mean free path and the higher dislocation recovery rate for the martensitic phase are indicators of a larger density of dislocations in this micro-constituent.

Figure 15 shows the predicted hardening curves for the three hot-stamped microstructures based on the calculated flow response for the corresponding micro-constituents (Figure 14) compared with the experimental data. The results exhibit good agreement between the predicted and measured hardening curves for all three die-quenched microstructures.

In hot stamping, the mechanical response of final components is strongly dependent on the quenching condition so that any local changes in the pre-set tooling temperature and contact pressure can significantly alter the mechanical properties of the products. In practice, variations in quenching rates are inevitable in commercial hot-stamping operations due to factors such as changes in tooling temperatures between the startup and steady-state production conditions as well as die wear altering the contact pressure. Therefore, there is a need to understand the influence of variability in quench rates on the final mechanical properties. To develop a more generalized predictive model along with this perspective, the martensite carbon contents in the reference microstructures (Table 6) were fit to an exponential function (Equation (22)) in terms of the martensite volume fraction ($V_M$) with three calibration parameters of $a$, $b$, and $c$.

Table 8. The values of calibration parameters ($a$, $b$, and $c$ ) of Equation (22) for the martensite carbon content ($\%C_M$ ) and MMC material parameters ($A$, $B$, and $C$ ).

Parameter	$\mathit{a}$	$\mathit{b}$	$\mathit{c}$
$\%C_M$ (wt.%)	0.6391	5.8713	0.0792
$A$	−0.1202	6.4922	1.1744
$B$	−0.0001	−6.5147	0.2051
$C$	−0.0430	−3.8798	−1.1050

presents the obtained values for these parameters.

$$f(V_M)=a\exp (-b{V}_M)+c$$

(22)

Then the carbon concentrations in martensite and bainite within Ductibor^® 1000-AS bainitic-martensitic microstructures with varied micro-constituent contents were calculated using the calibrated exponential function and carbon mass balance (Equation (12)), respectively (see Figure 16).

Next, the hardening response of the micro-constituents was computed using Rodriguez and Gutierrez’s model (Equation (8) [43]), and accordingly, the flow behavior of the multi-phase microstructures was predicted using the current MFH approach. Figure 17 and Figure 18 show the predicted hardening curves for the constituent phases and corresponding mixed-phase microstructures, respectively. The predictions indicate that as more martensitic phase is formed, the strength of martensite itself decreases (Figure 17a), while the relevant mixed-phase microstructure strengthens (Figure 18). These results are in line with the experimental and numerical data reported by Golling et al. [20] on bainitic-martensitic microstructures of the AlSi-coated 22MnB5 (Usibor^® 1500-AS) steel. The weakening of martensite is related to an inverse correlation between its carbon concentration and quantity (Figure 16). However, the strengthening of the overall microstructure can be attributed to the stronger influence of the martensite amount, which remains the harder phase in the microstructure (as can be discerned from Figure 17). For example, martensite in a 90% bainite plus 10% martensite (90%B + 10%M) microstructure was predicted to have a carbon concentration of 0.43 wt.% and a strength level of ~2.3 GPa, while increasing the martensite amount to 100% resulted in a carbon content of 0.081 wt.% and a strength measure of ~1.2 GPa for this phase. Meanwhile, the strength of the overall microstructure was predicted to increase by around 37%.

The results also show that the strength of bainite, contrary to martensite, does not change noticeably with its volume fraction. Such a trend is attributed to the insignificant variations predicted in the carbon content of the bainitic phase compared to that in martensite (Figure 16) and is in accord with the earlier studies by Young and Bhadeshia [56] and Golling et al. [62] on bainitic-martensitic microstructures of different steels. The increase in the martensite content (or the decrease in the bainite amount) resulted in an initial drop and then a smooth, continuous increase in the bainite carbon content (Figure 16) and, consequently, its strength (Figure 17b). Young and Bhadeshia [56] also estimated a transition in bainite strength with its volume fraction in their analytical calculations but within tempered bainitic-martensitic microstructures of a high-strength steel. Another difference between the predicted hardening response for the bainitic and martensitic phases is related to the manner of their work hardening. As seen in Figure 17, martensite initially shows an extensive work-hardening rate and a rapid stress saturation afterward. However, bainite exhibits continuous work hardening to larger strains. Such predictions seem physically reasonable since martensite is a harder phase with a much larger number of dislocations and, consequently, a higher rate of dislocation recovery [43,63].

It is worth mentioning that in the current study, analogous to the study by Ramazani et al. [44,64], the micro-constituent dislocation mean free paths and recovery rates were assumed to be constant in different microstructures. In reality, these parameters change with phase quantities, sizes, and morphology. Given the good agreement between the predicted and measured data in terms of the macroscopic flow response of the hot-stamped microstructures (Figure 15), it seems that the error accompanied with such assumptions has been limited by the calibrated carbon concentrations.

4.4.2. Predicted Fracture Response

As noted in Section 3.2, the 100%B and 100%M fracture loci were considered to be the fracture limits of bainite and martensite in the numerical modelling, respectively. Since a 100%B microstructure could not be produced for the range of the hot-stamping conditions considered in the current work, the fracture locus of this microstructure in the computations was estimated by the extrapolation of the trend in the MMC material parameters with the martensite content in the available microstructures (Figure 19). In this regard, constants of the MMC fracture model were fit to the exponential functions in the form of Equation (22), and then those for the 100%B microstructure were calculated using the calibrated interpolation functions. The values of the calibration parameters of these functions are presented in Table 8. It is noted that in the damage modelling, the optimized values of the GISSMO damage exponent (Equation (15)) for the bainitic and martensitic phases, obtained based on the 100%B and 100%M fracture loci, were 0.56 and 0.51, respectively.

Figure 20 shows the predicted fracture strains of the reference bainitic-martensitic (350 °C and 450 °C die-quenched) microstructures in each fracture test compared with the experimental data. The predicted and measured fracture strains are in good accord so that the predictions lie either within or close to the experimental ranges. It is noteworthy that the predictions revealed the onset of fracture within the bainitic phase in the hole-expansion and Nakazima tests and within the martensitic phase in the shear and plane-strain notch tension tests for the 350 °C die-quenched microstructure (~25%B + 75%M). However, fracture was predicted to occur within bainite in all of the fracture tests for the 450 °C die-quenched microstructure (~70%B + 30%M).

Figure 21 displays the fracture loci predicted for the reference multi-phase microstructures in comparison with their experimentally based MMC fracture curves. The 100%B and 100%M fracture limits are also exhibited as the upper and lower bounds, respectively. It is observed that the predicted fracture curves are in accord with the experimentally based MMC fracture loci.

Given the successful predictions of the fracture curves for the developed multi-phase microstructures, the established damage predictive tool was utilized to predict variations in the Ductibor^® 1000-AS fracture locus for bainitic-martensitic microstructures with various phase quantities. The predictions presented in Figure 22 imply that more martensite content corresponds to overall reduced ductility. Such a trend is compatible with the empirical data for the developed microstructures in this study. These predictions, together with the calculated corresponding flow response (Figure 18), represent the key material data required to take account of the influence of variable cooling conditions in hot stamping on the mechanical performance of final components.

5. Conclusions

This research has contributed towards the quantification of the relationship between the microstructure and mechanical behavior in Ductibor^® 1000-AS subjected to hot stamping. The following conclusions stem from this study:

(1)

The microstructure, flow, and fracture response of Ductibor^® 1000-AS are quench-rate sensitive within the range of cooling rates considered during hot stamping. A decrease in the cooling rate from 243 °C/s to 21 °C/s resulted in a 70% drop in the martensite content of the microstructure, a 26% reduction in UTS, and a 40–60% increase in the fracture strain for most of the investigated loading conditions.

(2)

The established numerical scheme based upon a hybrid micromechanical and phenomenological methodology predicted the hardening and fracture response in the multi-phase microstructures of the 350 °C and 450 °C die-quenched Ductibor^® 1000-AS with reasonable accuracy.

(3)

Predictions for the hardening and fracture curves of the Ductibor^® 1000-AS bainitic-martensitic microstructures with varied phase quantities revealed that a higher fraction of martensite results in the strengthening of the steel but at the expense of ductility.

(4)

Microscopic predictions demonstrated that with an increased martensite content in bainitic-martensitic microstructures of Ductibor^® 1000-AS, the martensitic phase weakens, while the bainitic phase exhibits a transition from weakening to strengthening at a low martensite volume fraction.