Next Article in Journal / Special Issue
Metallographic Index-Based Quantification of the Homogenization State in Extrudable Aluminum Alloys
Previous Article in Journal
Metal Injection Molding (MIM) of Magnesium and Its Alloys
Previous Article in Special Issue
Effect of Surface States on Joining Mechanisms and Mechanical Properties of Aluminum Alloy (A5052) and Polyethylene Terephthalate (PET) by Dissimilar Friction Spot Welding
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Metals
Volume 6
Issue 5
10.3390/met6050120
metals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The Influence of Specimen Thickness on the Lüders Effect of a 5456 Al-Based Alloy: Experimental Observations

by
Yu-Long Cai
,
Su-Li Yang
,
Shi-Hua Fu
and
Qing-Chuan Zhang
*
Chinese Academy of Science Key Laboratory of Mechanical Behavior and Design of Materials, University of Science and Technology of China, Hefei 230027, China
*
Author to whom correspondence should be addressed.
Metals 2016, 6(5), 120; https://doi.org/10.3390/met6050120
Submission received: 11 March 2016 / Revised: 16 May 2016 / Accepted: 17 May 2016 / Published: 20 May 2016
(This article belongs to the Special Issue Aluminum Alloys)
Browse Figures
Versions Notes

Abstract

:
For the first time ever, a thickness dependence of the Lüders effect in an Al-based alloy is demonstrated. A three-dimensional digital image correlation method was used to gain insight into the Lüders band velocity and the Lüders strain. The results revealed that both the strain and velocity depend on the specimen thickness. The strain increases, whereas the velocity decreases, with decreasing specimen thickness. Moreover, the plot of the strain vs. the velocity concurs with the global deformation compatibility.

Graphical Abstract

1. Introduction

Owing to their low density, high strength, and good formability, Al-based alloys are extensively used in the automotive industry [1]. These properties are advantageous from a manufacturing point of view. However, the heterogeneous deformation of Al-based alloys (even at room temperature) subjected to a high strain gradient represents a major drawback of these materials. This phenomenon leads to undesirable visible traces on the surface of the final products [2,3]. The induced heterogeneous deformation can be classified into two general categories: the Lüders effect and the Portevin-Le Chatelier (PLC) effect. These effects are governed by different microscopic mechanisms. The PLC effect is typically attributed to dynamic interactions between mobile dislocations and diffusing solutes (i.e., dynamic strain ageing, DSA) [4,5,6]. On the other hand, the Lüders effect results from both the dislocation pinning/unpinning effect arising from Cottrell atmosphere constraints and the collective or self-organized dislocation multiplication and motion [7,8,9,10,11]. According to the Johnston theory [12,13], dislocation pinning by impurity atmospheres does not occur in materials with low densities of mobile dislocations. This seems to contradict the Cottrell theory [14], which describes locking or unlocking behaviors. However, these theories actually complement each other, as the low mobile dislocation density stems from the previously completed pinning process.
The Lüders effect, referred to as the yield point phenomenon, is characterized by a sharp yield point and a subsequent yield plateau. An ideal plastic plateau, due to the propagation of a localized plastic deformation, is manifested; the occurrence of this plateau is accompanied by a decrease in the yield stress. Studies focused on the features of the Lüders effect, e.g., the Lüders strain, the Lüders band velocity, or the morphology of the Lüders bands, have been conducted in recent years. These studies revealed that the Lüders strain is affected by the applied strain rate [8,15], solute concentration [15,16,17,18], test temperature [19], and the grain size [18,20,21]. For example, Johnson et al. [15], Winlock [16], Song et al. [17], and Tsuchida et al. [18] determined the influence of the carbon content on the magnitude of the Lüders strain in steel; in all cases, the strain exhibited a negative dependence on the carbon content. Jin et al. [20], Lloyd et al. [21], and Tsuchida et al. [18] found that the yield stress (in accordance with the Hall-Petch relationship) and the Lüders strain are both inversely proportional to the grain size. The digital image correlation (DIC) method and infrared thermography technique (IRT) have been used to perform kinematic and calorimetric analyses of Lüders bands. Nagarajan et al. [9,10] used DIC and IRT to determine the spatio-temporal evolution of the full-field strain and temperature contours; this yielded an improved understanding of band nucleation and propagation as well as the band growth mechanism. IRT has been used to determine spatial characteristics, such as the shape, orientation, and velocity [22] and morphological characteristics, such as the X-, Y- and V-shaped patterns [23] of Lüders bands. Based on the aforementioned experimental results, theoretical models, which takes both Cottrell atmosphere pinning and dislocation multiplication into consideration, have been used to describe the features of spatial coupling [13,24,25].
Since Yoshida et al. [7] reported a thickness dependence of the plastic behavior of 4–30 μm thick copper whiskers, a few studies have focused on this thickness dependence, on the millimeter scale, in polycrystals. In this work, we determine the influence of the thickness on the Lüders strain, Lüders band velocity, and the correlation between these features in a 5456 Al-based alloy.

2. Materials and Methods

The chemical composition (wt. %) of the 5456 Al-based alloy is shown in Table 1. Large plates of the alloy were subjected to an aging heat treatment (annealing at 673 K for 3 h followed by furnace-cooling to room temperature); dumbbell-shaped plate specimens were then cut from these plates. These 55 mm (gage length) × 20 mm (width) specimens had different thicknesses (t = 1, 2, and 3 mm). The stiffness of the testing machine influences the PLC effect and the Lüders plateau [26,27]. We used a hard machine, referred to as RGM-4050 (Reger Instrument Co., Ltd., Shenzhen, China), to determine the thickness dependence of the Lüders effect. Uniaxial tensile tests were performed at room temperature and constant strain rates ranging from 1.82 × 10−4 to 90.9 × 10−4 s−1. The applied tensile load was recorded at a sampling rate of ~25 Hz.
The three-dimensional DIC (3D-DIC) method is applied in the present study for surface strain mapping; this non-contact method is used to measure the full-field space coordinate, displacement, and strain distributions in a material. This method is precise, accurate, does not require special quakeproof equipment, and is therefore widely used in material testing [28,29]. 3D-DIC is adept at measuring strain localization. Optical methods, such as shadowgraphy [30], laser scanning extensometry [31], and digital speckle pattern interferometry [2,3] obtain indirect observations of the localized bands, and hence quantitative analysis is difficult. Direct images can be readily obtained using 3D-DIC. The accuracy of this method was determined through a coupling factor that takes into account the image noise, interpolation bias, and the calculation algorithm parameters [32]. Establishing the theoretical measurement resolution for high-gradient deformation conditions (e.g., within Lüders or the PLC band) is difficult. Specifically, the experiment value of the displacement and strain measurement error are ~0.01 pixels and 150 με, respectively [33]. In a previous study, we determined the effect of DIC parameters, such as the patch size, shape function, and the strain gradient, on the measurement error; based on the results, a moderate patch size was suggested for high-gradient inhomogeneous deformation [29].
In the present study, a self-developed 3D-DIC system (PMLAB DIC-3D; Nanjing PMLAB Sensor Tech Co., Ltd., Nanjing, China) was used to continuously capture deformed images (via synchronous image acquisition) at an image sampling rate of 3 fps. So-called sequence DIC and equal-interval DIC were both used in this work. In the case of sequence DIC, the correlation between a fixed reference image and the deformed image is determined; with equal-interval DIC, however, the correlation between frame n and frame n + g is determined (g is the image interval; g = 1, time interval ≈ 1/3 s in this work). Prior to the tensile tests, specimens were sprayed with a flat white lacquer and then oversprayed with random black spots. The following dimensions were used in the 3D-DIC system: array dimensions of each image = 2048 × 2048 pixels; calculation grid size = 7 pixels; patch size = 29 × 29 pixels; strain calculation window size = 15 × 15 points. A correspondence of ~16 pixel/mm was obtained between the real dimension and the acquired image. The right-handed coordinate was defined as follows: the transverse direction and the tensile direction were the X and Y axes, respectively.

3. Results

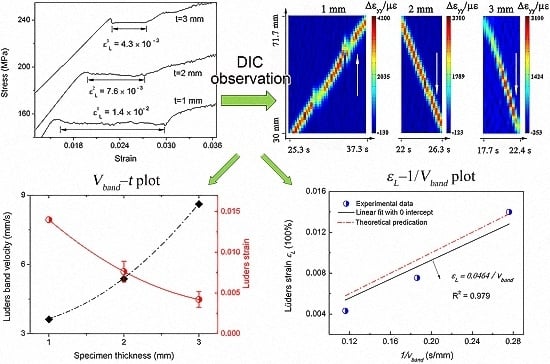
3.1. Lüders Strain

Figure 1 shows the engineering stress–strain curves, obtained at an applied strain rate of 9.09 × 10−4 s−1, for specimens with different thicknesses. For clarity, we have depicted the curves separated vertically by a stress interval of 35 MPa. The inset indicates that the Lüders strain, i.e., the length of the Lüders plateau formed during straining, decreases with increasing specimen thickness. A PLC effect is visible almost immediately after the Lüders effect. It consists of a serrated flow with numerous stress drops. These serrations are of similar characteristics for the three tests. These results indicate that the specimen thickness influences the Lüders effect. In contrast, the PLC effect seems not to be influenced by the specimen thickness.
As previously stated, the specimen thickness has a pronounced effect on the Lüders strain. Therefore, specimens of different thicknesses were subjected to uniaxial tensile tests at various applied strain rates to determine the dominant factor (thickness or strain rate). Figure 2 shows the Lüders strain as a function of the specimen thickness. Data corresponding to the 2-mm-thick and 3-mm-thick specimens were obtained from six and four tests performed at strain rates ranging from 9.09 × 10−4 to 0.909 × 10−4 s−1 and 1.82 × 10−4 to 9.09 × 10−4 s−1, respectively. In fact, previous studies [8,15] have revealed a power-law dependence of the Lüders strain on the strain rate. However, this dependence was not observed in the present study. The insets of Figure 2 show the Lüders strain of the 2- and 3-mm specimens as a function of the applied strain rate. The strain increases with increasing strain rate, albeit with some scatter, which to a certain extent contradicts previous studies. Compared to the applied strain rate, the specimen thickness generally has a more pronounced effect on the Lüders strain. Figure 2 confirms a negative relationship between the strain and specimen thickness.

3.2. Lüders Band Velocity

As a form of plastic instability, the Lüders effect differs compared to the PLC effect mainly on the serration morphology and the strain-localized band propagation. Generally, the continuous sweep corresponds to the smooth plateau of the Lüders effect; nevertheless, the propagation of PLC bands can be continuous, hopping, and even random along the specimen with abrupt serrations. Here, to exhibit the difference in the straining process of these two types of plastic instabilities, we present the example of the 1-mm specimen. Figure 3a shows the illustration of the selected data for DIC calculations. Figure 3b,c respectively show the accumulated-strain mappings of the Lüders and PLC band. It can be seen that the Lüders band manifests as a continuous localized deformation band from one end of the specimen to the other. The PLC bands were characterized by discrete strip bands which belong to type B serrations. The DIC results revealed that the strain in the tensile direction of the PLC band is much higher than that of the Lüders band.
As previously stated, the Lüders strain is correlated with the specimen thickness. Usually, a yield plateau occurs during the propagation process of a Lüders band; hence, the dependence of the Lüders band velocity on the specimen thickness was subsequently explored. Figure 4 shows the strain mapping (both the equal-interval strain mapping (a) and the accumulated-strain mapping (b)) along the tensile direction of specimens with different thicknesses. The strain rate of the test was 9.09 × 10−4 s−1. Figure 4a shows that localized deformation occurs within an inclined strip only, and then propagates from one end of the specimen to the other. The growing stair (or step) in the accumulated strain mappings (Figure 4b) reveals the propagation of the Lüders band. As the figure shows, the Lüders band velocity (in contrast to the Lüders strain) exhibits a positive dependence on the specimen thickness (see Figure 4c).

3.3. Global Deformation Compatibility

A single Lüders band propagates at a constant velocity along the gage length of the specimen [15]. This propagation may be expressed mathematically as follows:
εLl0 = Vcrosshead
where εL, Δt = l0/Vband, l0, , Vcrosshead, and Vband are the Lüders strain, the duration of the plateau, gage length, the velocities of the crosshead of the test machine, and the Lüders band, respectively. Equation (1) indicates that the Lüders plateau ends immediately after the band sweeps the entire specimen. Rewriting Equation (1) yields:
εL = Vcrosshead/Vband
Equation (2) reveals that the Lüders strain, the applied strain rate, and the Lüders band velocity satisfy the global deformation compatibility requirement, in accordance with the theoretical predictions of Hall et al. [34] and Estrin et al. [35]. Furthermore, this relationship does not rely on the specimen thickness, whereas the Lüders strain only depends on the thickness. Therefore, at a given applied strain rate, the band velocity and strain exhibit opposite dependences on the specimen thickness; moreover, for a given thickness, the velocity is proportional to the applied strain rate.
The aforementioned results indicate that a plot of the Lüders strain vs. the Lüders band velocity can only be obtained by considering specimens of differing thicknesses. As Figure 5 shows, the relationship between the strain and the velocity concurs with the predicted tendency.

3.4. Spatial Characteristics

Figure 6 shows the displacement and strain mappings, including the in-plane and out-of-plane displacement, of specimens with different thicknesses. A Lüders band is clearly visible in each specimen. We note that, in all cases, the localized-deformation region lies almost completely within a strip inclined at ~60° with respect to the tensile direction. However, the band inclination in Figure 6a is >60°, resulting possibly from the crossover of localized bands with different orientations. This is verified by Figure 7, where the crossover evolution of the localized band in a 1-mm-thick specimen is revealed. As the figure shows, growth of the partial band leads to changes in the band inclination. The inclination of the band front (with respect to the tensile direction) increases, gradually leading, eventually, to a nearly flat band (the newly formed band in Figure 6a and Figure 7). Hill [36] attributed the occurrence of necking to the plastic flow of anisotropic metals. Analysis (including the concept of von Mises plasticity) of the strain localization under plane stress uniaxial tension yields the classical value (~54.74°) of the band inclination in an isotropic sheet; this value is moderately lower than the experimentally determined value obtained in the present study. We have shown [37] that the deformation mode of the PLC localized region under uniaxial tensile tests in the sheet plane is simple shear, which demonstrates that the strain-localized region appears along the shear direction. Based on our research, the Lüders band and the PLC band are similar in macroscopic deformation, which probably implies the same deformation mode. Coer et al. [38] investigated the Lüders effect of an Al-Mg alloy during the simple shear tests; the literature gave direct observations of the localized deformation at the simple shear state. These two studies all reveal that the strain-localization and the simple shear state have some sort of inner link, which needs more effort to explore.
Experimentally, the localized deformation in the out-of-plane displacement field is obtained due to the incompressibility during the plastic stage. In fact, the maximum out-of-plane displacement increases with increasing thickness at a maximum strain increment (~3000 με), which is consistent with our previous study on PLC bands [39]. The in-plane displacement mappings (profiles on the left-hand side of Figure 6) show that the distance between the band front and band tail generally increases with increasing specimen thickness. This spatial characteristic was investigated in further detail.
Here we define the width of the Lüders band (wband) as follows: the distance at the mid-height of the localized strain band of the strain increment (see Figure 8). The maximum strain increment (εmax) of the Lüders band is defined as the maximum strain increment value of the center line (Line 0 in Figure 8a). Figure 8 shows the dependence of wband and εmax (obtained at a fixed image-sampling rate of 3 fps) on the specimen thickness, for a given strain rate of 9.09 × 10−4 s−1. As the figure shows, εmax and wband remain approximately constant and increase, respectively, with increasing specimen thickness.
As previously mentioned, the Lüders band velocity increases with increasing specimen thickness. Consistent with the results shown in Figure 9, wband increases owing to continuous propagation of the band. The band sweeps the gage length of the specimen (in general); hence, the accumulated strain varies with the equal-interval maximum strain increment and the equal-interval band width. However, the obtained experimental results reveal that the accumulated strain depends only on wband. This strain increases with increasing specimen thickness, consistent with the results shown in Figure 4b.

4. Conclusions

We investigated the dependence of the Lüders effect on specimen thickness. Characteristics, such as the Lüders strain, Lüders band velocity, and the correlation between these features, were determined by using the 3D-DIC method. The major conclusions can be summarized as follows:
(1)
This is the first report demonstrating the dependence of the Lüders strain on the specimen thickness of a 5456 Al-based alloy.
(2)
The Lüders strain increases, but the Lüders band velocity decreases, with decreasing specimen thickness.
(3)
Uniquely, the plot of the Lüders strain vs. the Lüders velocity was obtained via direct observation.

Acknowledgments

The authors gratefully acknowledge the financial support received from the National Natural Science Foundation of China (NSFC) under grant No. 11332010, 51271174, and 11372300.

Author Contributions

Yu-Long Cai performed the experiments, analyzed the data, and wrote the paper; Shi-Hua Fu, Su-Li Yang and Qing-Chuan Zhang discussed the results.

Conflicts of Interest

The authors declare no conflict of interests.

References

  1. Fridlyander, I.N.; Sister, V.G.; Grushko, O.E.; Berstenev, V.V.; Sheveleva, L.M.; Ivanova, L.A. Aluminum alloys: Promising materials in the automotive industry. Met. Sci. Heat Treat. 2002, 44, 365–370. [Google Scholar] [CrossRef]
  2. Zhang, Q.; Jiang, Z.; Jiang, H.; Chen, Z.; Wu, X. On the propagation and pulsation of Portevin-Le Chatelier deformation bands: An experimental study with digital speckle pattern metrology. Int. J. Plast. 2005, 21, 2150–2173. [Google Scholar] [CrossRef]
  3. Jiang, H.; Zhang, Q.; Jiang, Z.; Wu, X. Experimental investigations on kinetics of Portevin-Le Chatelier effect in Al-4wt. %Cu alloys. J. Alloys Compd. 2007, 428, 151–156. [Google Scholar] [CrossRef]
  4. Benallal, A.; Berstad, T.; Børvik, T.; Hopperstad, O.S.; Koutiri, I.; Nogueira de Codes, R. An experimental and numerical investigation of the behaviour of AA5083 aluminium alloy in presence of the Portevin-Le Chatelier effect. Int. J. Plast. 2008, 24, 1916–1945. [Google Scholar] [CrossRef]
  5. Fu, S.; Cheng, T.; Zhang, Q.; Hu, Q.; Cao, P. Two mechanisms for the normal and inverse behaviors of the critical strain for the Portevin-Le Chatelier effect. Acta Mater. 2012, 60, 6650–6656. [Google Scholar] [CrossRef]
  6. Cai, Y.; Tian, C.; Fu, S.; Han, G.; Cui, C.; Zhang, Q. Influence of γ’ precipitates on Portevin-Le Chatelier effect of Ni-based superalloys. Mater. Sci. Eng. A 2015, 638, 314–321. [Google Scholar] [CrossRef]
  7. Yoshida, K.; Gotoh, Y.; Yamamoto, M. The thickness dependence of plastic behaviors of copper whiskers. J. Phys. Soc. Jpn. 1968, 24, 1099–1107. [Google Scholar] [CrossRef]
  8. Sun, H.B.; Yoshida, F.; Ohmori, M.; Ma, X. Effect of strain rate on Lüders band propagating velocity and Lüders strain for annealed mild steel under uniaxial tension. Mater. Lett. 2003, 57, 4535–4539. [Google Scholar] [CrossRef]
  9. Nagarajan, S.; Narayanaswamy, R.; Balasubramaniam, V. Advanced imaging for early prediction and characterization of zone of Lüders band nucleation associated with pre-yield microstrain. Mater. Sci. Eng. A 2013, 561, 203–211. [Google Scholar] [CrossRef]
  10. Nagarajan, S.; Narayanaswamy, R.; Balasubramaniam, V. Study on local zones constituting to band growth associated with inhomogeneous plastic deformation. Mater. Lett. 2013, 105, 209–212. [Google Scholar] [CrossRef]
  11. Van Rooyen, G.T. The stress and strain distribution in a propagating Lüders front accompanying the yield-point phenomenon in iron. Mater. Sci. Eng. 1968, 3, 105–117. [Google Scholar] [CrossRef]
  12. Johnston, W.G.; Gilman, J.J. Dislocation velocities, dislocation densities, and plastic flow in lithium fluoride crystals. J. Appl. Phys. 1959, 30, 129–144. [Google Scholar] [CrossRef]
  13. Hahn, G.T. A model for yielding with special reference to the yield-point phenomena of iron and related bcc metals. Acta Metall. 1962, 10, 727–738. [Google Scholar] [CrossRef]
  14. Cottrell, A.H.; Bilby, B.A. Dislocation theory of yielding and strain ageing of iron. Proc. Phys. Soc. 1949, 62. [Google Scholar] [CrossRef]
  15. Johnson, D.H.; Edwards, M.R.; Chard-Tuckey, P. Microstructural effects on the magnitude of Lüders strains in a low alloy steel. Mater. Sci. Eng. A 2015, 625, 36–45. [Google Scholar] [CrossRef]
  16. Winlock, J. The influence of the rate of deformation on the tensile properties of some plain carbon sheet steels. J. Metall. 1953, 5, 797–803. [Google Scholar]
  17. Song, R.; Ponge, D.; Raabe, D. Improvement of the work hardening rate of ultrafine grained steels through second phase particles. Scr. Mater. 2005, 52, 1075–1080. [Google Scholar] [CrossRef]
  18. Tsuchida, N.; Tomota, Y.; Nagai, K.; Fukaura, K. A simple relationship between Lüders elongation and work-hardening rate at lower yield stress. Scr. Mater. 2006, 54, 57–60. [Google Scholar] [CrossRef]
  19. Fisher, J.C.; Rogers, H.C. Propagation of Lüder's bands in steel wires. Acta Metall. 1956, 4, 180–185. [Google Scholar] [CrossRef]
  20. Jin, H.; Lloyd, D.J. Effect of a duplex grain size on the tensile ductility of an ultra-fine grained Al-Mg alloy, AA5754, produced by asymmetric rolling and annealing. Scr. Mater. 2004, 50, 1319–1323. [Google Scholar] [CrossRef]
  21. Lloyd, D.; Court, S.A.; Gatenby, K.M. Lüders elongation in Al-Mg alloy AA5182. Mater. Sci. Technol. 1997, 13, 660–666. [Google Scholar] [CrossRef]
  22. Louche, H.; Chrysochoos, A. Thermal and dissipative effects accompanying Lüders band propagation. Mater. Sci. Eng. A 2001, 307, 15–22. [Google Scholar]
  23. Delpueyo, D.; Balandraud, X.; Grediac, M. Calorimetric signature of the Portevin-Le Chatelier effect in an aluminum alloy from infrared thermography measurements and heat source reconstruction. Mater. Sci. Eng. A 2016, 651, 135–145. [Google Scholar] [CrossRef]
  24. Mazière, M.; Forest, S. Strain gradient plasticity modeling and finite element simulation of Lüders band formation and propagation. Continuum Mech. Thermodyn. 2015, 27, 83–104. [Google Scholar] [CrossRef]
  25. Wenman, M.R.; Chard-Tuckey, P.R. Modelling and experimental characterisation of the Lüders strain in complex loaded ferritic steel compact tension specimens. Int. J. Plast. 2010, 26, 1013–1028. [Google Scholar] [CrossRef]
  26. Wang, H.D.; Berdin, C.; Mazière, M.; Forest, S.; Prioul, C.; Parrot, A.; Le-Delliou, P. Experimental and numerical study of dynamic strain ageing and its relation to ductile fracture of a C-Mn steel. Mater. Sci. Eng. A 2012, 547, 19–31. [Google Scholar] [CrossRef]
  27. Nadai, A. Theory of Flow and Fracture of Solids; McGraw Hill: New York, NY, USA, 1950; Volume 1. [Google Scholar]
  28. Gao, Y.; Cheng, T.; Su, Y.; Xu, X.; Zhang, Y.; Zhang, Q. High-efficiency and high-accuracy digital image correlation for three-dimensional measurement. Opt. Laser Eng. 2015, 65, 73–80. [Google Scholar] [CrossRef]
  29. Xu, X.; Su, Y.; Cai, Y.; Cheng, T.; Zhang, Q. Effects of various shape functions and subset size in local deformation measurements using DIC. Exp. Mech. 2015, 55, 1575–1590. [Google Scholar] [CrossRef]
  30. Chihab, K.; Estrin, Y.; Kubin, L.P.; Vergnol, J. The kinetics of the Portevin-Le Chatelier bands in an Al-5 at. % Mg alloy. Scr. Metall. 1987, 21, 203–208. [Google Scholar] [CrossRef]
  31. Ziegenbein, A.; Hhner, P.; Neuhuser, H. Correlation of temporal instabilities and spatial localization during Portevin-Le Chatelier deformation of Cu-10 at. % Al and Cu-15 at. % Al. Comput. Mater. Sci. 2000, 19, 27–34. [Google Scholar] [CrossRef]
  32. Su, Y.; Zhang, Q.; Gao, Z.; Xu, X.; Wu, X. Fourier-based interpolation bias prediction in digital image correlation. Opt. Express 2015, 23, 19242–19260. [Google Scholar] [CrossRef] [PubMed]
  33. Sutton, M.A.; Turner, J.L.; Bruck, H.A.; Chae, T.A. Full-field representation of discretely sampled surface deformation for displacement and strain analysis. Exp. Mech. 1991, 31, 168–177. [Google Scholar] [CrossRef]
  34. Hall, E.O. Yield Point Phenomena in Metals and Alloys, 1st ed.; Plenum Press (a Division of Plenum Publishing Corporation): New York, NY, USA, 1970; pp. 34–35. [Google Scholar]
  35. Estrin, Y.; Kubin, L.P. Continuum Models for Materials with Microstructures; Wiley: New York, NY, USA, 1995; p. 395. [Google Scholar]
  36. Hill, R. A theory of the yielding and plastic flow of anisotropic metals. Proc. R. Soc. A Math. Phys. Eng. Sci. 1948, 193, 281–297. [Google Scholar] [CrossRef]
  37. Cai, Y.L.; Zhang, Q.C.; Yang, S.L.; Fu, S.H.; Wang, Y.H. Characterization of the deformation behaviors associated with the serrated flow of a 5456 Al-based alloy using two orthogonal digital image correlation systems. Mater. Sci. Eng. A 2016, 664, 155–164. [Google Scholar] [CrossRef]
  38. Coer, J.; Manach, P.Y.; Laurent, H.; Oliveira, M.C.; Menezes, L.F. Piobert-Lüders plateau and Portevin-Le Chatelier effect in an Al-Mg alloy in simple shear. Mech. Res. Commun. 2013, 48, 1–7. [Google Scholar] [CrossRef]
  39. Cai, Y.L.; Zhang, Q.C.; Yang, S.L.; Fu, S.H.; Wang, Y.H. Experimental study on three-dimensional deformation field of Portevin-Le Chatelier effect using digital image correlation. Exp. Mech. 2016, 1–13. [Google Scholar] [CrossRef]
Metals 06 00120 g001 1024
Figure 1. Engineering stress-strain curves obtained at 9.09 × 10−4 s−1 for specimens with different thicknesses. For clarity, these curves are separated vertically by a stress interval of 35 MPa. The inset provides a magnified view of the Lüders plateaus.
Figure 1. Engineering stress-strain curves obtained at 9.09 × 10−4 s−1 for specimens with different thicknesses. For clarity, these curves are separated vertically by a stress interval of 35 MPa. The inset provides a magnified view of the Lüders plateaus.
Metals 06 00120 g001
Metals 06 00120 g002 1024
Figure 2. Dependence of the Lüders strain on the specimen thickness at various applied strain rates. The insets show the strain as a function of the strain rate at a given specimen thicknesses.
Figure 2. Dependence of the Lüders strain on the specimen thickness at various applied strain rates. The insets show the strain as a function of the strain rate at a given specimen thicknesses.
Metals 06 00120 g002
Metals 06 00120 g003 1024
Figure 3. Test on a 1-mm-thick specimen at 9.09 × 10−4 s−1. (a) Stress-strain curve that shows selected image data for digital image correlation (DIC) calculation; (b) Longitudinal strain maps revealing the Lüders effect; (c) Longitudinal strain maps revealing the Portevin-Le Chatelier (PLC) effect. Reference images are defined at ~18.3 and ~425.6 s, respectively. Sequence DIC method was used for this processing.
Figure 3. Test on a 1-mm-thick specimen at 9.09 × 10−4 s−1. (a) Stress-strain curve that shows selected image data for digital image correlation (DIC) calculation; (b) Longitudinal strain maps revealing the Lüders effect; (c) Longitudinal strain maps revealing the Portevin-Le Chatelier (PLC) effect. Reference images are defined at ~18.3 and ~425.6 s, respectively. Sequence DIC method was used for this processing.
Metals 06 00120 g003
Metals 06 00120 g004 1024
Figure 4. Test on three different thickness specimens at 9.09 × 10−4 s−1. (a) Equal-interval strain mapping; (b) Accumulated-strain mapping in the tensile direction; (c) Dependence of the Lüders band velocity and the Lüders strain on the specimen thickness, at a fixed strain rate of 9.09 × 10−4 s−1. The white arrows in (a) and (b) denote the propagation directions. The time interval in the equal-interval DIC calculation is approximately 1/3 s.
Figure 4. Test on three different thickness specimens at 9.09 × 10−4 s−1. (a) Equal-interval strain mapping; (b) Accumulated-strain mapping in the tensile direction; (c) Dependence of the Lüders band velocity and the Lüders strain on the specimen thickness, at a fixed strain rate of 9.09 × 10−4 s−1. The white arrows in (a) and (b) denote the propagation directions. The time interval in the equal-interval DIC calculation is approximately 1/3 s.
Metals 06 00120 g004
Metals 06 00120 g005 1024
Figure 5. Relationship between the Lüders strain and the Lüders band velocity. The theoretical prediction can be expressed as: ε L = 3   mm 60   s × 1 V band = 0.05 × 1 V band .
Figure 5. Relationship between the Lüders strain and the Lüders band velocity. The theoretical prediction can be expressed as: ε L = 3   mm 60   s × 1 V band = 0.05 × 1 V band .
Metals 06 00120 g005
Metals 06 00120 g006 1024
Figure 6. Test on three different thickness specimens at 9.09 × 10−4 s−1. The Lüders band, for specimens of differing thicknesses, as determined via the equal-interval DIC method; 1-mm-, 2-mm-, and 3-mm-thick specimens are shown in (a–c), respectively. Incremental results are presented (i.e., (a–c) show the correlation between frames 72 and 73, frames 80 and 81, and frames 118 and 119, respectively. Furthermore, u and εyy are the respective displacement and strain increment in the tensile direction, and w is the out-of-plane displacement increment.
Figure 6. Test on three different thickness specimens at 9.09 × 10−4 s−1. The Lüders band, for specimens of differing thicknesses, as determined via the equal-interval DIC method; 1-mm-, 2-mm-, and 3-mm-thick specimens are shown in (a–c), respectively. Incremental results are presented (i.e., (a–c) show the correlation between frames 72 and 73, frames 80 and 81, and frames 118 and 119, respectively. Furthermore, u and εyy are the respective displacement and strain increment in the tensile direction, and w is the out-of-plane displacement increment.
Metals 06 00120 g006
Metals 06 00120 g007 1024
Figure 7. Crossover evolution of the Lüders band in a 1-mm-thick specimen at 9.09 × 10−4 s−1. Sequence DIC method was used, and frame 65 was considered as the reference image. Changes in the band inclination are induced by growth of the partial band. This growth (frames 67–69) leads to a change in the band front direction.
Figure 7. Crossover evolution of the Lüders band in a 1-mm-thick specimen at 9.09 × 10−4 s−1. Sequence DIC method was used, and frame 65 was considered as the reference image. Changes in the band inclination are induced by growth of the partial band. This growth (frames 67–69) leads to a change in the band front direction.
Metals 06 00120 g007
Metals 06 00120 g008 1024
Figure 8. Test on a 2-mm-thick specimen at 9.09 × 10−4 s−1. Schematic showing the calculation of the Lüders band width. The strain mapping in (a) was performed via equal-interval digital image correlation method (frame 80 and 81). The strain distribution along the Y-direction, (b), was determined for Line 0 in (a).
Figure 8. Test on a 2-mm-thick specimen at 9.09 × 10−4 s−1. Schematic showing the calculation of the Lüders band width. The strain mapping in (a) was performed via equal-interval digital image correlation method (frame 80 and 81). The strain distribution along the Y-direction, (b), was determined for Line 0 in (a).
Metals 06 00120 g008
Metals 06 00120 g009 1024
Figure 9. Dependence of the width and the maximum strain increment of the Lüders band on the specimen thickness, for a given strain rate of 9.09 × 10−4 s−1.
Figure 9. Dependence of the width and the maximum strain increment of the Lüders band on the specimen thickness, for a given strain rate of 9.09 × 10−4 s−1.
Metals 06 00120 g009
Table
Table 1. Chemical composition (wt. %) of the 5456 Al-based alloy.
Table 1. Chemical composition (wt. %) of the 5456 Al-based alloy.
ElementsMgMnFeSiZnTiCuCrAl
Content4.7–5.50.5–1.00.40.250.250.20.10.05–0.2Balance

Share and Cite

MDPI and ACS Style

Cai, Y.-L.; Yang, S.-L.; Fu, S.-H.; Zhang, Q.-C. The Influence of Specimen Thickness on the Lüders Effect of a 5456 Al-Based Alloy: Experimental Observations. Metals 2016, 6, 120. https://doi.org/10.3390/met6050120

AMA Style

Cai Y-L, Yang S-L, Fu S-H, Zhang Q-C. The Influence of Specimen Thickness on the Lüders Effect of a 5456 Al-Based Alloy: Experimental Observations. Metals. 2016; 6(5):120. https://doi.org/10.3390/met6050120

Chicago/Turabian Style

Cai, Yu-Long, Su-Li Yang, Shi-Hua Fu, and Qing-Chuan Zhang. 2016. "The Influence of Specimen Thickness on the Lüders Effect of a 5456 Al-Based Alloy: Experimental Observations" Metals 6, no. 5: 120. https://doi.org/10.3390/met6050120

APA Style

Cai, Y. -L., Yang, S. -L., Fu, S. -H., & Zhang, Q. -C. (2016). The Influence of Specimen Thickness on the Lüders Effect of a 5456 Al-Based Alloy: Experimental Observations. Metals, 6(5), 120. https://doi.org/10.3390/met6050120

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop