Monotonic and Cyclic Behavior of DIN 34CrNiMo6 Tempered Alloy Steel
Abstract
:1. Introduction
2. Experimental Procedure
2.1. Materials
2.2. Monotonic Tensile Tests
2.3. Low-Cycle Fatigue Tests
2.4. Analysis of Material Microstructure
2.5. Analysis of Fracture Surfaces
3. Results and Discussion
3.1. Microstructure
3.2. Monotonic Behavior
3.3. Cyclic Behavior
3.3.1. Cyclic Stress-Strain Response
3.3.2. Low-Cycle Fatigue Properties
3.3.3. Analysis of Fracture Surfaces
4. Conclusions
- The material exhibited a fine microstructure mainly composed of martensite and lower bainite. The average grain size obtained from the procedure described by the ASTM E112 standard was about 8 μm. As usual in this high-strength steel, inclusions with different sizes, ranging from 2 to 30 μm, were found;
- The monotonic behavior of the material was investigated from uniaxial tensile tests conducted according to the procedure described in the ASTM E8 standard. The monotonic stress-strain curve was characterized by a yield point elongation (0.59% < ε < 2.4%); an ultimate tensile strength recorded for a total strain equal to 8.7%; and a large region of non-uniform plastic deformation with a maximum total strain greater than 17.2%. The fracture surfaces revealed a mixed mechanism involving microvoid coalescence and cleavage;
- The cyclic plastic behavior of the material was studied under fully-reversed strain-controlled conditions. A strain-softening phenomenon was observed throughout the entire life. This behavior was identified regardless of the strain amplitude. The degree of softening was in line with the results available in the literature, i.e., a first stage of rapid increase (up to Δε/2 < 0.52%) and a second stage of progressive and smooth reduction;
- The effective elastic unloading modulus (E’), defined as the slope of the linear portion of the stable hysteresis loop upon strain reversal from the maximum load, varied with the cyclic characteristic of this steel. The softening behavior observed here caused a decrease in E’;
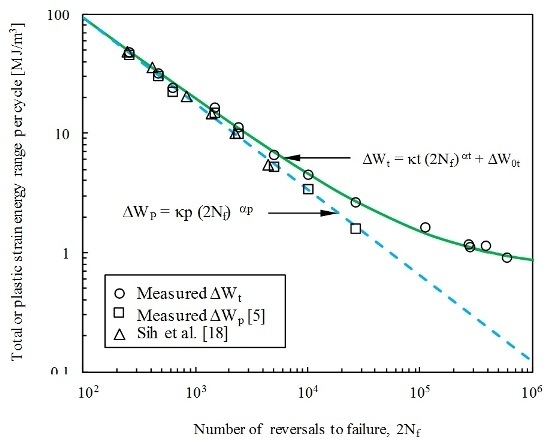
- The total strain energy density, defined as the sum of both tensile elastic and plastic strain energies, was revealed to be an adequate fatigue damage parameter for short and long lives. On the other hand, the plastic strain energy density is more recommended for shorter lives;
- The SEM micrographs evidenced transgranular crack propagation. For higher strain amplitudes, initiation sites revealed a blend of cleavage facets with areas of ductile dimples; for lower amplitudes, initiation sites were dominated by cleavage facets.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Murty, Y.V.; Morral, J.E.; Kattamis, T.Z.; Mehrabian, R. Initial coarsening of manganese sulfide inclusions. Metall. Mater. Trans. 1975, 6A, 2031–2039. [Google Scholar] [CrossRef]
- Lee, W.S.; Su, T.T. Mechanical properties and microstructural features of AISI 4340 high-strength alloy steel under quenched and tempered conditions. J. Mater. Proc. Technol. 1999, 87, 198–206. [Google Scholar] [CrossRef]
- Costa, J.D.; Ferreira, J.M.; Ramalho, A.L. Fatigue and fretting fatigue of ion-nitrided 34CrNiMo6 steel. Theor. Appl. Fract. Mech. 2001, 35, 69–79. [Google Scholar] [CrossRef]
- Tartaglia, J.; Lazzari, K.; Hui, G.; Hayrynen, K. A comparison of mechanical properties and hydrogen embrittlement resistance of austempered vs. quenched and tempered 4340 steel. Metall. Mater. Trans. 2008, 39A, 559–576. [Google Scholar] [CrossRef]
- Branco, R.; Costa, J.D.; Antunes, F.V. Low-cycle fatigue behaviour of 34CrNiMo6 high strength steel. Theor. Appl. Fract. Mech. 2012, 58, 28–34. [Google Scholar] [CrossRef]
- Branco, R.; Costa, J.D.; Antunes, F.V. Fatigue behaviour and life prediction of lateral notched round bars under bending-torsion loading. Eng. Fract. Mech. 2014, 199, 66–84. [Google Scholar] [CrossRef]
- Boardman, B. Properties and Selection: Irons, Steels and High-Performance Alloys: Fatigue Resistance of Steels. In ASM Handbook; ASM: Materials Park, OH, USA, 2000; Volume 1, pp. 673–688. [Google Scholar]
- Smith, R.W.; Hirschberg, M.H.; Manson, S.S. Fatigue Behaviour of Materials under Strain Cycling in Low and Intermediate Life Range; NACA TN D-1574; National Advisory Committee for Aeronautics: Washington, DC, USA, 1963. [Google Scholar]
- Pape, J.; Neu, R. A comparative study of the fretting fatigue behavior of 4340 steel and PH 13-8 Mo stainless steel. Int. J. Fatigue 2007, 29, 2219–2229. [Google Scholar] [CrossRef]
- Ramberg, W.; Osgood, W.R. Description of Stress-Strain Curves by Three Parameters; NACA TN 902; National Advisory Committee for Aeronautics: Washington, DC, USA, 1943. [Google Scholar]
- Ellyin, F. Fatigue Damage, Crack Growth and Life Prediction, 1st ed.; Chapman & Hall: London, UK, 1997. [Google Scholar]
- Basquin, O.H. The exponential law of endurance tests. Am. Soc. Test. Mater. ASTM 1910, 10, 625–630. [Google Scholar]
- Morrow, J.D. Cyclic plastic strain energy and fatigue of metals. In International Friction, Damping and Cyclic Plasticity; ASTM STP 378; ASTM: West Conshohocken, PA, USA, 1965; pp. 45–87. [Google Scholar]
- Coffin, L.F. A study effects of cyclic thermal stresses on ductile metal. Trans. ASME 1954, 76, 931–950. [Google Scholar]
- Manson, S.S. Behaviour of Materials under Conditions of Thermal Stress; NACA TN-2933; National Advisory Committee for Aeronautics: Washington, DC, USA, 1954. [Google Scholar]
- Endo, T.; Morrow, J. Cyclic stress-strain and fatigue behavior of representative aircraft metals. J. Mater. 1969, 4, 159–175. [Google Scholar]
- Tartaglia, J.; Hayrynen, K. A Comparison of fatigue properties of austempered versus quenched and tempered 4340 steel. J. Mater. Eng. Perform. 2012, 21, 1008–1024. [Google Scholar] [CrossRef]
- Sih, G.C.; Jeong, D.Y. Hysteresis loops predicted by isoenergy density theory for Polycrystals. Part II: Cyclic heating and cooling effects predicted from nonequilibrium theory for 6061-T6 aluminum, SAE 4340 steel and Ti-8Al-1Mo-1V titanium cylindrical bars. Theor. Appl. Fracture Mech. 2004, 41, 267–289. [Google Scholar] [CrossRef]
- Golos, K.; Ellyin, F. Generalization of cumulative damage criterion to multilevel cyclic loading. Theor. Appl. Fracture Mech. 1987, 7, 169–176. [Google Scholar] [CrossRef]
- Rabb, R. Fatigue failure of a connecting rod. Eng. Fail. Anal. 1996, 3, 13–28. [Google Scholar] [CrossRef]













| Element | C | Si | Mn | Cr | Mo | Ni |
|---|---|---|---|---|---|---|
| Weight (%) | 0.34 | ≤0.40 | 0.65 | 1.50 | 0.22 | 1.50 |
| Mechanical Property | Value a | Value b [7] |
|---|---|---|
| Yield strength, σYS (MPa) | 967 | 860 |
| Ultimate tensile strength, σUTS (MPa) | 1035 | 1020 |
| Elongation, εR (%) | 18 | 20 |
| Reduction of area, RA (%) | 58 | 60 |
| Property | Value |
|---|---|
| Coefficient κp (MJ/m3) | 2115.84 |
| Exponent αp | −0.6924 |
| Coefficient κt (MJ/m3) | 2165.37 |
| Exponent αt | −0.6854 |
| Constant ΔW0t (MJ/m3) | 0.7049 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Branco, R.; Costa, J.D.M.; Antunes, F.V.; Perdigão, S. Monotonic and Cyclic Behavior of DIN 34CrNiMo6 Tempered Alloy Steel. Metals 2016, 6, 98. https://doi.org/10.3390/met6050098
Branco R, Costa JDM, Antunes FV, Perdigão S. Monotonic and Cyclic Behavior of DIN 34CrNiMo6 Tempered Alloy Steel. Metals. 2016; 6(5):98. https://doi.org/10.3390/met6050098
Chicago/Turabian StyleBranco, Ricardo, José D. M. Costa, Fernando V. Antunes, and Sandra Perdigão. 2016. "Monotonic and Cyclic Behavior of DIN 34CrNiMo6 Tempered Alloy Steel" Metals 6, no. 5: 98. https://doi.org/10.3390/met6050098
APA StyleBranco, R., Costa, J. D. M., Antunes, F. V., & Perdigão, S. (2016). Monotonic and Cyclic Behavior of DIN 34CrNiMo6 Tempered Alloy Steel. Metals, 6(5), 98. https://doi.org/10.3390/met6050098