Welding Distortion Prediction in 5A06 Aluminum Alloy Complex Structure via Inherent Strain Method

Abstract

Finite element (FE) simulation with inherent deformation is an ideal and practical computational approach for predicting welding stress and distortion in the production of complex aluminum alloy structures. In this study, based on the thermal elasto-plastic analysis, FE models of multi-pass butt welds and T-type fillet welds were investigated to obtain the inherent strain distribution in a 5A06 aluminum alloy cylindrical structure. The angular distortion of the T-type joint was used to investigate the corresponding inherent strain mechanism. Moreover, a custom-designed experimental system was applied to clarify the magnitude of inherent deformation. With the mechanism investigation of welding-induced buckling by FE analysis using inherent deformation, an application for predicting and mitigating the welding buckling in fabrication of complex aluminum alloy structure was developed.

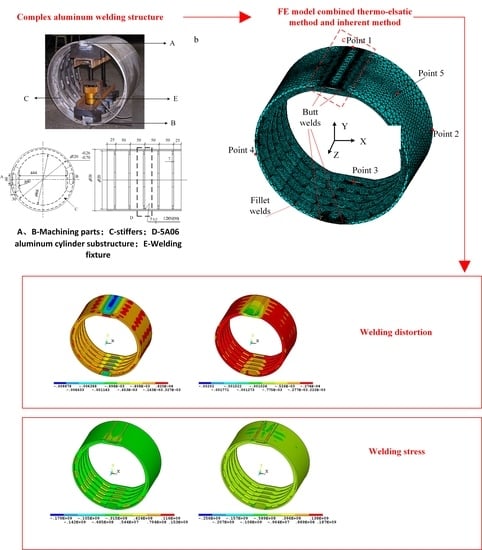
1. Introduction

Residual stresses and distortions are two of the major concerns in welded structures, especially for aluminum alloy thin-walled structures [1,2]. Welding stresses and distortion cause dimensional deviation due to the highly localized, non-uniform, transient heating and subsequent cooling of the welded material, and the non-linearity of aluminum material properties [3]. These stresses lead to the crucial cracking after welding. Particularly tensile residual stresses near the weld area cause stress rising, fatigue failure and brittle fracture [4,5].

Validating methods for predicting welding stresses and distortion are desirable because of the complexity of the welding process. Accordingly, finite element (FE) simulation has become a popular tool for the prediction of welding residual stresses and distortion [6,7,8]. Many investigators have developed the analytical and experimental methods to predict the welding residual stresses. Da Nóbrega et al. evaluated the temperature field and residual stresses in a multi-pass weld of API 5L X80 steel using the finite element method [9]. Zeng et al. predicted the thermal elasto-plastic analysis using finite element techniques to analyze the thermo-mechanical behavior and evaluate the residual stresses and distortion of 5A06 aluminum alloy structure in discontinuous welding [10]. Syahroni and Hidayat focused on numerical simulation of welding sequence effect on temperature distribution, residual stresses and distortions of T-joint fillet welds [11]. Normally, the commercial welding software SYSWELD Weld Planner provides access to welding-induced distortion simulation even for people unfamiliar with finite element simulation at the early stage of preliminary design and planning, and ESI Distortion Engineering can comprise the former and offer services to solve welding problems [12]. However, new heat source models or material properties for novel materials need to be built up based on basic interdisciplinary studies rather than direct application of commercial software. For large and complex welded structures applied in the marine, ship and aerospace fields, the models developed by the thermal elastic-plastic finite element method need to be divided into a large number of grids and time steps, which are not applicable in the actual work. Therefore, the inherent strain method is an alternative for estimating the overall welding distortions [13,14,15]. It is noted that the inherent strain method induces the transient effect of the welding process to inherent strain key parameters, avoiding the transient analysis of numerical simulation and the computational difficulty in high temperature, reducing the calculation time and obtaining the residual stress and deformation value with a certain degree of accuracy [16]. Few studies have explored the welding multi-physics mechanism in detail despite its high efficiency in calculating the size and distribution of inherent strain with a certain accuracy in the numerical simulation of complex welded structures, especially for fillet joint angular distortion. The prerequisite of this method is that the inherent deformations (i.e., longitudinal shrinkage, transverse shrinkage, angular distortion and longitudinal bending) in each joint should be known beforehand [17].

In this paper, the purpose is to investigate the quantitative relationship between the inherent strain and the structural factor during the welding process and analyze the welding residual stresses and distortion of the 5A06 aluminum alloy structure. The method combined initial thermo-elastic-plastic analysis with the inherent strain method developed in this paper, illustrating much more feasibility and accuracy for a complex welding structure in terms of the effects of welding sequence and weldment size, compared to the empirical formula or data of the commercial welding simulation software. Two models, a multi-pass V-type butt weld and T-type fillet-welded joint, were used to analyze the size and distribution of the inherent strain. The inherent strain mechanism was discussed by analyzing the angular distortion of the T-type joint. Moreover, the effect of buckling deformation was also investigated.

2. Model Analysis

A 5A06 aluminum alloy structure with an outer diameter of 538 mm, thickness of 9 mm, and length of 250 mm was examined in this paper. There are five identical cylinder substructures combined to form the structure. In order to control the distortion, stiffeners were welded onto the structure. Welding condition is shown in

Table 1. Welding condition parameters.

Welding Parameters	U (V)	I (A)	Welding Speed (cm·min−1)	Wire Feed Rate (cm·min−1)
Value	26.2	286	50–60	15.7–20

, and the composition of the 5A06 aluminum alloy used in this investigation is shown in

Table 2. Chemical composition of 5A06 aluminum alloy.

Composition	ω (Si)	ω (Cu)	ω (Mg)	ω (Zn)	ω (Mn)	ω (Ti)	ω (Fe)	ω (Al)
Mass fraction	0.004	0.001	0.058–0.068	0.002	0.005–0.008	0.0002–0.001	0.004	balance

. Figure 1a,b showed the welding structure. The central axis of the welding fixture was parallel to the workplace radial direction. Meanwhile, there were several claws supporting rigidly on the workplace wall in the circumferential direction during the welding process. At the same time, the force on the claw acted on the inclined plane below through a lower supporting structure and a rolling wheel. The inclined plane was connected to the central axis. The welding stress could transfer to the claws, then to the tooling, which could prevent large deformation during the welding process.

As no metallurgical phase transformation occurs in the aluminum alloy used in this work, the volumetric effects due to the phase transformation on residual stress evolution are not considered here; the procedure seems acceptable to achieve accurate stress and distortion distribution in references [18]. Since welding processes undergo a high temperature cycle and exhibit material properties that are temperature dependent, the thermal and mechanical properties of the 5A06 aluminum alloy in

Table 3. Material properties of 5A06 aluminum alloy.

Materials Properties	Temperature, °C
Name	20	100	200	500	587	630
Young’s modulus (GPa)	70	70	61	41.	10	1
Linear expansion coefficient (10−6·K−1)	0.93 × 10−4	1.91	4.50	13.3	15.9	17.6
Poisson’s ratio	0.35	0.35	0.35	0.35	0.35	0.35
Density (kg·m−3)	2750	2730	2710	2640	2630	2450
Specific heat (J·kg−1·K−1)	898	951	1003	1150	1195	1165
Yield stress (MPa)	130	100	54	10	5	5

were determined by the Probability Design System (PDS) in the finite element software ANSYS [19]. The FE model and the butt welds for inherent strain estimation are shown in Figure 2. In the mechanical analysis, the fillet welds’ thermal stresses and distortion were calculated from the temperature distribution determined by thermal elasto-plastic FE model in references [10,20]. The material was assumed to follow the Von Mises yield criterion and flow rule here. The 20-node hexahedral element SOLID185 was applied in this investigation. These thermal strains of SOLID185 element change linearly for stress analysis. Moreover, the element thermal strain can be confirmed if each node’s mutative temperature and anisotropic thermal expansion coefficient matrix are defined, i.e., inherent strain components could be mapped to the elasto-plastic model in forms of t equivalent thermal strain.

3. Welding Distortion Prediction in Thin Plate Fabrication by Means of Inherent Strain FE Method

In the FE elements, the Mindlin plate theory was employed and the geometrical nonlinear effect was also considered. Considering transverse shear strain components, the total strains could be expressed as follows [16].

$${\mathsf{\epsilon }}_x={\mathsf{\epsilon }}_x^i+{\mathsf{\epsilon }}_x^b=\left[\frac{\partial u}{\partial x}+\frac{1}{2}{\left(\frac{\partial w}{\partial x}\right)}^2\right]+\left[-z\frac{{\partial }^{2}w}{\partial x^2}+z\frac{\partial {\mathsf{\theta }}_y}{\partial x}\right]$$

(1)

$${\mathsf{\epsilon }}_y={\mathsf{\epsilon }}_y^i+{\mathsf{\epsilon }}_y^b=\left[\frac{\partial v}{\partial y}+\frac{1}{2}{\left(\frac{\partial w}{\partial y}\right)}^2\right]+\left[-z\frac{{\partial }^{2}w}{\partial y^2}-z\frac{\partial {\mathsf{\theta }}_x}{\partial y}\right]$$

(2)

$${\mathsf{\gamma }}_{xy}={\mathsf{\gamma }}_{xy}^i+{\mathsf{\gamma }}_{xy}^b=\left[\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}+\left(\frac{\partial w}{\partial x}\right)\left(\frac{\partial w}{\partial y}\right)\right]+\left[-2z\frac{{\partial }^{2}w}{\partial x\partial y}+z\frac{\partial {\mathsf{\theta }}_y}{\partial y}-z\frac{\partial {\mathsf{\theta }}_x}{\partial x}\right]$$

(3)

$${\mathsf{\gamma }}_{xz}={\mathsf{\theta }}_y+\frac{\partial w}{\partial x}$$

(4)

$${\mathsf{\gamma }}_{yz}=-{\mathsf{\theta }}_x+\frac{\partial w}{\partial y}$$

(5)

where u and v are in-plane displacements at mid-plane; w is out-of-plane displacements; θ_x and θ_y are rotations; ${\mathsf{\epsilon }}_x$, ${\mathsf{\epsilon }}_y$, ${\mathsf{\gamma }}_{xy}$ are total strains, and ${\mathsf{\epsilon }}_x^i$, ${\mathsf{\epsilon }}_y^i$ and ${\mathsf{\gamma }}_{xy}^i$ are in-plane strains; ${\mathsf{\epsilon }}_x^b$ and ${\mathsf{\epsilon }}_y^b$ and ${\mathsf{\gamma }}_{xy}^b$ are bending strains, ${\mathsf{\gamma }}_{xz}$ and ${\mathsf{\gamma }}_{yz}$, are transverse shear strains.

The curvature K_x in a plane parallel to the x–z plane and the curvature K_y in a plane parallel to the y–z plane and the twisting curvature K_xy, which represents the warping of the x–y plane, can be defined as follows.

$${\kappa }_x=-\frac{{\partial }^{2}w}{\partial x^2}$$

(6)

$${\kappa }_y=-\frac{{\partial }^{2}w}{\partial y^2}$$

(7)

$${\kappa }_{xy}=-\frac{{\partial }^{2}w}{\partial x\partial y}$$

(8)

In the present FEM, three types of inherent deformations, namely longitudinal shrinkage, transverse shrinkage and angular distortion are introduced into the elastic FEM. When a welding line is arranged parallel to the x-axis, longitudinal shrinkage can be transformed into in-plane strain component ${\mathsf{\epsilon }}_x$ in longitudinal direction. As mentioned above, another equivalent method is to use tendon force to represent longitudinal shrinkage. Transverse shrinkage can be changed into in-plane strain component ${\mathsf{\epsilon }}_y$ in transverse direction. In a similar way, angular distortion can be converted into curvature K_x along the x-axis. These inherent strain components are introduced into the elastic FEM as initial strains.

4. Results and Discussion

In this paper, the thermo-elastic-plastic FE method was used to estimate the welding stress and distortion in the welds including the butt welds and fillet welds with inherent stain.

4.1. Inherent Strain Analysis of Butt Weld and Fillet Welds

As mentioned above, the welding stress and distortion in complex welding structures were mostly caused by longitudinal and transverse inherent strains. In order to obtain the size and distribution of inherent strain after welding and determine the quantitative relationship between the inherent strain and the primary influence factors, a sequential coupling of thermal-elasto-plastic analytical method was employed to acquire the value of inherent strain of two typical welded joints in Figure 2b. Figure 3 showed the distribution of longitudinal and transverse residual stresses of butt-joint with multi-passes. It was found that the tensile stress was widely distributed in the center of welded seams and localized in the edge region. Most of the welding area was under in the tensile stress. With the increase of heat input, the longitudinal and transverse tensile stresses of the second layer’s welded seam rose up gradually. When reaching the yield limit, the value of residual tensile stresses was stable, but their distribution area increased. This was due to residual thermal contraction deformation caused by the cooling down of filler metal [21]. Herein, residual compressive plastic deformation and residual thermal contraction deformation are both attributed to inherent strain.

Figure 4 explains the distribution of longitudinal and transverse residual plastic strains of the butt joint. Obviously, most of the weld zone was plastically deformed in a compressive state except for both ends. The residual strain in the center of the welded seams was stable but their distribution area increased similar to the stress distributions. Figure 5 shows the distribution of the welding residual stress and plastic strain of path A-A (as shown in Figure 2b). The residual strain was concentrated in the vicinity of the welded seams. Moreover, both longitudinal and transverse directions were under compressive deformation. Meanwhile, the residual plastic strain in the transverse direction was larger than that in the longitudinal direction, whereas the strain away from the seam was almost zero. In the welding zone, the welding residual stress was tensile stress, and the longitudinal residual stress was much greater than the transverse direction. Correspondingly, the adjacent area of welded seams displayed compressive stress. When moving backwards to the welded seams, the stress decayed. When the weldment exceeded a certain length, the longitudinal and transverse inherent strain coefficients were insignificantly changed except for the arc initiation and closing positions [22]. The influence of the weld length on the W3 and W4-welded seams was similar to that of the W1 and W2. In addition, the inherent strain coefficients of the W3 and W4-welded seams were slightly decreased because of the reduced thermal gradients.

The three-dimensional uncoupled thermo-mechanical FE analysis was carried out to produce the temperature distribution, residual stresses and distortion on fillet welds of the aluminum alloy structure in the discontinuous welding, illustrating factors of angular distortion and the effects of weld sequence on residual stress distributions. The simulated results demonstrated that the temperature gradient through thickness was a main factor that strongly governs the generation of angular distortion in a fillet-welded joint. The angular distortion decreased because of the preheating and reheating during the discontinuous welding. However, the temperature lagging between the external surface and internal surface aggravated the angular distortion. Welding sequences and weld length are greatly important to residual stresses and distortion [10,20].

In the prediction methods of welding residual stress and distortion, such as the inherent strain method and the volumetric shrinkage method, the boundary condition imposed by the welds and the effect of actual inherent strain distribution on the structure directly determine the prediction accuracy. Like all strain tensors, the inherent strain had six strain components in different directions. The residual stress and distortion were from the comprehensive interaction of all these six components. The simplification in current prediction methods was based on the correspondence of residual stresses and distortion with the chosen components of inherent strain. For example, we used the inherent strain method to predict longitudinal residual stress, longitudinal shrinkage deformation and bending deformation by exerting boundary conditions corresponding to longitudinal inherent strain in the welds through ignoring inherent strains in other directions. Similarly, the boundary values related to transversing the inherent strain on welded seams could be set to predict the transverse residual stress. Through this, the prediction of transverse residual stress, the transverse shrinkage deformation and the angular distortion were possible and could be used to predict welding shrinkage distortion and butt-welding angular distortion of the plate. However, this was invalid for angular distortion of the fillet weld [23].

The deformation deviation caused by insufficient data of inherent strain and uncertain volumetric shrinkage in the welded seam could be reduced by improving the database or empirical formula [24]. However, the simplification method is attributed to the determination of the relationship between the inherent strain component and welding deformation. The mechanism of welding deformation is one of the key aspects of this simplification method. In this work, the mapping of the inherent strain component was used to analyze the relationship between angular distortion and the inherent strain component of the fillet weld.

Here, the data of the inherent strain component existing in the welded structure was analyzed through the thermal elasto-plastic analysis using finite element techniques. The deformation of different inherent strain components acting alone could then be obtained by linear elasticity calculation. Compared to such angular distortion with standard welding angular distortion (angular distortion from thermal elasto-plastic analysis), the effect of inherent strain on welding angular distortion could be analyzed. For example, the conversion formula corresponding to the temperature change of inherent strain components $\Delta T_{xx}=(x,y,z)$ can be written as,

$$\Delta T_{xx}(x,y,z)=\frac{{\mathsf{\epsilon }}_{xx}(x,y,z)}{{\mathsf{\alpha }}_{xx}}$$

(9)

where ${\mathsf{\alpha }}_{xx}=C$, C is a constant. The corresponding material with anisotropic thermal expansion coefficient is defined as: ${\mathsf{\alpha }}_{xx}=C$, ${\mathsf{\alpha }}_{yy}={\mathsf{\alpha }}_{zz}={\mathsf{\alpha }}_{xy}={\mathsf{\alpha }}_{xz}={\mathsf{\alpha }}_{yz}=0$. Other mechanical parameters and physical parameters are assumed as constant values at room temperature. The same method works on other five inherent strain components.

The standard deformation measured using elasto-plastic analysis is ${\mathsf{\delta }}^{EPA}(x,y,z)$. The inherent strain component is expressed as ${\mathsf{\epsilon }}_{ij}(x,y,z)$, and then the deformation, taking welding structure into account, only is $f({\mathsf{\epsilon }}_{ij}(x,y,z))$. Theoretically, ${\mathsf{\delta }}^{EPA}(x,y,z)$ = ${\mathsf{\delta }}^{sum}(x,y,z)$. The relative error of numerical results is as follows.

$$\text{error}=\frac{{\mathsf{\delta }}^{sum}-{\mathsf{\delta }}^{EPA}}{{\mathsf{\delta }}^{EPA}}\times 100\%$$

(10)

As shown in Figure 4, the end of the joint was with an upward displacement because of a positive component of transverse inherent strain ${\mathsf{\epsilon }}_{xx}$. However, the actual displacement was smaller than the standard value. From the angular distortion results, including the mapping of the inherent positive strain component ${\mathsf{\epsilon }}_{yy}$, ${\mathsf{\epsilon }}_{zz}$, T-joint panels produced a very small amount of negative angular distortion under the influence of positive inherent strain in two directions, i.e., the larger angle of fillet weld after deformation. The calculation results of angular distortion using the mapping of inherent shear strain component ${\mathsf{\epsilon }}_{xy}$ indicated that the end of the T-joint panel warped upwards and the magnitude of displacement was close to the standard value. In addition, other strains ${\mathsf{\epsilon }}_{yz}$${\mathsf{\epsilon }}_{xz}$ were very small suggesting that the inherent shear strain components from these two directions almost had no effect on the angular distortion of the fillet weld.

In the study of the mapping of strain components in Figure 6, the sum of average value of angular distortion Φ₀ of the panel’s free end caused by six separate inherent strain components was 0.448 mm. The standard value, however, was 0.496 mm, meaning the error was only 1.6% according to the simulation.

The relationship between the angular distortion and the inherent strain component was inconsistent. It depended on the welding structure and joint configuration including workplace thickness, height of weld leg and welding conditions, etc. From the thermo-elastic-plastic analysis, the component of inherent shear strain ${\mathsf{\epsilon }}_{xy}$ had an obvious effect on the angular distortion of fillet weld close to standard value. The effect of a positive component of transverse inherent strain on angular distortion ${\mathsf{\epsilon }}_{xx}$ was smaller than ${\mathsf{\epsilon }}_{xy}$. The other two components ${\mathsf{\epsilon }}_{yy}$, ${\mathsf{\epsilon }}_{zz}$ would cause a small negative angular distortion. Also, the influence of the components of inherent shear strain ${\mathsf{\epsilon }}_{yz}$ and ${\mathsf{\epsilon }}_{xz}$ on angular distortion could be ignored. This was also in agreement with the report in references [25]. Therefore, ${\mathsf{\epsilon }}_{xy}$ was the greatest influence factor on angular distortion of fillet weld among the six components of inherent strain, which determined the final angular distortion.

4.2. Analysis of the Aluminum Alloy Structure

The SOLID 185 was used to mesh the model into 172,680 elements and 66,513 nodes. As shown in Figure 1, aluminum ring 1 to 5 were specified from the z-axis-positive direction to negative direction and calculated through the inherent strain method according to analysis of the multi-pass longitudinal welded seam and discontinuous fillet weld.

In ANSYS, the values of inherent strain cannot be directly loaded. However, the anisotropic thermal expansion coefficient can reflect different contractions in both longitudinal and transverse directions. Therefore, it is associated with the temperature load of units that can be used to apply loads. The thermal expansion coefficient is the value of strain.

$$\mathsf{\epsilon }=W/F=\mathsf{\alpha }\cdot \Delta T$$

(11)

where, W stands for the total amount of welding shrinkage in per unit length. F is the cross-sectional area of unit locating in inherent strain. α represents the thermal expansion coefficient equal to the numerical value of inherent strain. T is the temperature load of each unit. The strain load was applied to welded seam and adjacent units. Before computing, a few aspects should be addressed: Thermal expansion coefficients of longitudinal s and transverse strain corresponded with the direction of welded seam; longitudinal and transverse strains were negative with an opposing symbol of temperature load; the directions without inherent strains set the thermal expansion coefficient as zero while the other elements were the same.

Since the fillet weld was not linear, converting the data according to the spatial direction of the weld and coordinate system of angular orientation was needed. In Figure 7, we assumed that welded seams extended along the X₀ direction with an angle of θ in the local coordinate system XOY. The formulas to calculate the welded seams were,

$${\mathsf{\epsilon }}_x={\mathsf{\epsilon }}_{x0} \text{cos}\mathsf{\theta }-{\mathsf{\epsilon }}_{y0} \text{sin}\mathsf{\theta }$$

(12)

$${\mathsf{\epsilon }}_y={\mathsf{\epsilon }}_{y0} \text{cos}\mathsf{\theta }-{\mathsf{\epsilon }}_{x0} \text{sin}\mathsf{\theta }$$

(13)

The calculated inherent strains of different welding joints were thus obtained as shown in

Table 4. Inherent strain on each weld joints.

Weld No.	Location	Joint Type	Cross-Section (mm2)	WX (mm2)	WY (mm2)	εx	εy	εxy
1	Stiffer front	T-joint	32	0.651	2.16	0.0204	0.067	0.0319
2	Stiffer front	T-joint	32	0.668	2.26	0.0208	0.071	0.0361
3	Stiffer front	T-joint	32	0.673	2.27	0.0210	0.072	0.0475
4	Stiffer front	T-joint	32	0.680	2.33	0.0212	0.073	0.0526
5	Stiffer front	T-joint	32	0.688	2.38	0.0215	0.074	0.0655
6	Stiffer front	T-joint	32	0.695	2.41	0.0217	0.076	0.0734
7	Stiffer front	T-joint	32	0.702	2.42	0.0219	0.076	0.0752
8	Stiffer front	T-joint	32	0.710	2.43	0.0222	0.076	0.0808
9	Stiffer front	T-joint	32	0.719	2.44	0.0225	0.077	0.0851
10	Stiffer front	T-joint	32	0.733	2.45	0.0229	0.077	0.0862
11	Stiffer front	T-joint	32	0.746	2.48	0.0233	0.078	0.0877
12	Stiffer front	T-joint	32	0.751	2.50	0.0235	0.079	0.0890
13	Stiffer back	T-joint	32	0.290	0.96	0.0090	0.030	0.0165
14	Stiffer back	T-joint	32	0.297	1.01	0.0092	0.031	0.0187
15	Stiffer back	T-joint	32	0.299	1.01	0.0093	0.031	0.0247
16	Stiffer back	T-joint	32	0.303	1.03	0.0094	0.032	0.0273
17	Stiffer back	T-joint	32	0.306	1.06	0.0095	0.033	0.0340
18	Stiffer back	T-joint	32	0.309	1.07	0.0096	0.034	0.0388
19	Stiffer back	T-joint	32	0.312	1.08	0.0097	0.034	0.0391
20	Stiffer back	T-joint	32	0.316	1.08	0.0099	0.034	0.0420
21	Stiffer back	T-joint	32	0.320	1.09	0.0100	0.034	0.0442
22	Stiffer back	T-joint	32	0.326	1.09	0.0102	0.034	0.0448
23	Stiffer back	T-joint	32	0.332	1.10	0.0104	0.035	0.0456
24	Stiffer back	T-joint	32	0.334	1.10	0.0105	0.035	0.0463
25	W1 (in Figure 1)	butt weld	18	0.729	2.67	0.0405	0.148	-
26	W2 (in Figure 1)	butt weld	40	0.756	2.75	0.0419	0.153	-
27	W3 (in Figure 1)	butt weld	18	0.960	3.11	0.0240	0.078	-
28	W4 (in Figure 1)	butt weld	40	0.934	3.01	0.0233	0.075	-

.

To verify the reliability of the simulation results, it is necessary to compare the results with experimental ones. A customized experimental facility (in Figure 8) was used to verify the FEM results in this paper. The residual stress measurement was mainly carried out by the hole-drilling method, cutting method, and X-ray diffraction method [26,27,28]. However, nearly all the stress experiments are not economically or conveniently suitable for such large-scale, complex structural components in this investigation. Thus, we developed a new method to verify the numerical simulation results with the welding compression load and strain tests. Normally, for thin-wall cylinder structure, significant contraction and wave distortion occur after welding. The stiffeners were welded separately for minimizing the contraction distortion. It is noted that the welding contraction load corresponds to the strain, which could be measured by the static resistance tester installed on the welding fixture. It means that the welding contraction load could be attained by measuring the strain on the welding fixture, which could also be predicted as residual stress by FEM using the inherent strain method. The relationship between strain and welding shrinkage strain is calibrated first which follows as Equation (14):

$$F=0.427+0.10169\mathsf{\mu }\mathsf{\epsilon }$$

(14)

In the equation, F stands for depressive load corresponding to the related strain. Thus, the welding shrinkage load or residual stress could be confirmed if the stains are measured before and after welding.

Before welding the stiffener, the strain was 105 με. According to the calibrated curve in Figure 8, the corresponding contraction load was acquired as 11 kN/240 mm, i.e., 3.833 MPa. Similarly, the strain value changed to 249 με after welding and the contraction load was 26 kN/240 mm, i.e., 11.479 MPa. Hereby, the welding strain and contraction load could be measured under different conditions.

According to the actual welding process, the inherent strains in Table 4 were imposed on each weld joints sequentially, and the depression load and welding stresses of the workplace were estimated through the thermal elasto-plastic finite element analysis. In Figure 9, After Fillet welds welding on the stiffer, the simulated residual stress in the Y direction (radial direction) of the workplace corresponding to the depression load on vertical supporting claws was calculated before and after stiffened plate welding. Obviously, the results of numerical simulation using the inherent strain method coincided with the experiment study.

Figure 10a,b shows the welding deformation of the structure at room temperature. With the welding process, the radial shrinkage of the structure decreased. The radial shrinkage at the lower edge of the last aluminum ring decreased about 30% more than the upper edge of aluminum ring. As above, the entire structure deformed within 2 mm in the condition of appropriate welding process and welding sequence. However, the position of stiffened plate was not web-plated; radial deformation at the position of the stiffened plate was significant, reaching up to 8 mm.

High residual stresses of the welding structure were shown in Figure 10c,d. The longitudinal residual stress of the welded seam reached about 120 MPa, while the residual stress of the 5A06 aluminum alloy cylinder reached about −40 MPa. The other positions such as the stiffened plate approached the yield strength of the 5A06 aluminum alloy.

4.3. Buckling Deformation Analysis

From the above analysis, the residual stress field in the thin plate developed gradually and formed tensile stress approaching the welded seams and compressive stress away from the welded seams. It was caused by the effect of the plastic deformation. This residual stress field was due to the uncoordinated weld zone (unevenness) instead of the external load, and it was a balanced stress field. If the value of residual compressive stress reached a critical load of the structure, the plate had a greater warpage out of the plane, namely buckling deformation.

In the foregoing analysis, the maximum deformation of the workplace was 8.8 mm (in Figure 10a), attributed to the category of small deflection theory analysis. Therefore, the balance method was adopted to analyze the critical yield load.

During the numerical simulation process, five testing points were selected to analyze whether the buckling deformation generated. These chosen points away from the welded seam were to avoid the result being influenced by the welding residual stress. The stress and strain were measured as shown in Figure 11. From points 2, 4, 5 of the cylinder, a conclusion can be drawn that the stress and strain on the cylinder were not uniform during the welding process including heating and cooling stages. Compared to the stress-strain curves of measured points 1 and 3, the mutation was produced by the deformation in which the stress changed smoothly. That is, the buckling deformation generated at the cooling time of 100 s after the stiffened plate was welded. Using the eigenvalue buckling analysis, the minimum eigenvalues of the structure could be calculated and its value was 0.676 (i.e., the critical loading of instability was equal to 1739 N).

Buckling deformation of a thin-walled structure was caused by two reasons. The first was the free deformation of aluminum metal located at the welded seams, whereby the near area was blocked at a high temperature, resulting in a compressive plastic deformation. The second was the angular distortion caused by the angle deformation of the fillet weld because of the uneven transverse shrinkage deformation in the thickness direction. Moreover, the deformation of the front side of the welded seam was large while its backside was small. It caused the plane component’s warpage. For the thin-plate welding with reinforced rib, the weld metal area was affected by compressive stress. During the cooling stage, the metals on both sides of the welded seam were influenced by compressive stress generating instability deformation. The final residual deformation depended on the final residual stress of the thin plate. Then the temperature during the cooling stage in the workplace tended to be uniform with balanced internal stresses. Therefore, the residual deformation also tended to be stable [29].

5. Conclusions

Based upon the thermal-elastic-plastic analysis of the discontinuous fillet welding, the inherent strain method was applied to the welding residual stress and deformation of a 5A06 aluminum alloy-reinforced cylinder structure, also taking into consideration the effects of welding technology and weldment size on the multi-pass V-type butt weld. It put great importance on the inherent strain distribution of joint type. For fillet welding, the relationship between the angular distortion and inherent strain component was inconsistent, depending on the welding structure and joint configuration. The shear inherent strain was the greatest influence on angular distortion of fillet weld among the six components of inherent strain, which determined the final angular distortion. It is noted that the wave propagation appeared in the stiffened plate during the welding, which caused the buckling deformation. The buckling deformation of this thin-walled structure was 8.8 mm, which mainly results from the non-uniform welding temperature distribution and angle deformation of the fillet weld. In order to ensure the dimensional accuracy, a post heat treatment might be needed to relieve stress of the thin-walled aluminum alloy structure. Compared to the experimental results of the welding depression load and strain, the inherent strain method has highly efficient and can ensure definite precision in the numerical simulation of the complex welding structure.