Numerical Modeling of Cyclic Deformation in Bulk Metallic Glasses
Abstract
:1. Introduction
2. Constitutive Relations of BMGs
3. FEM Modeling
4. Results and Discussion
4.1. Influence of Microstructure Heterogeneity in BMGs
4.2. Failure Mechanism in BMG under Cyclic Loading
4.3. Effect of Free Volume Fluctuation under Cyclic Loading
4.4. Effect of Applied Strain Amplitude
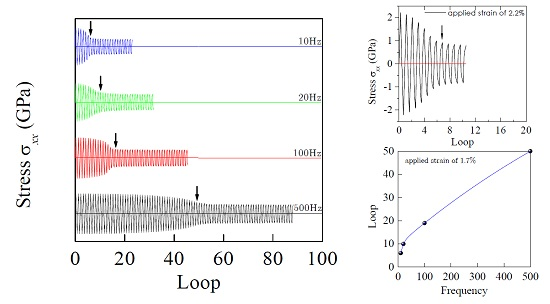
4.5. Effect of Loading Frequency
5. Conclusions
- (1)
- The heterogeneous distribution of initial defects has nearly no effect on the stress-strain relations of BMGs under uniaixal loading;
- (2)
- The applied strain amplitude significantly affects the fatigue life of BMGs, and the load drop cycle number markedly decreases with the increase in the strain amplitude;
- (3)
- For the applied strains in the range of the elastic stage, there is no further free volume accumulated in the BMG samples, and consequently no failure could be reached; and
- (4)
- For the BMG sample under cyclic loading, a stress drop in the stress–loops curves just corresponds to a main shear-band running across the sample. The fatigue life increases with increasing cycling frequency.
Acknowledgments
Conflicts of interest
References
- Jia, H.L.; Liu, F.X.; An, Z.N.; Li, W.D.; Wang, G.Y.; Chu, J.P.; Jang, J.S.C.; Gao, Y.F.; Liaw, P.K. Thin-film metallic glasses for substrate fatigue-property improvements. Thin Solid Films 2014, 561, 2–27. [Google Scholar] [CrossRef]
- Peter, W.H.; Liaw, P.K.; Buchanan, R.A.; Liu, C.T.; Brooks, C.R.; Horton, J.A.J.; Carmichael, C.A.J.; Wright, J.L. Fatigue behavior of Zr52.5Al10Ti5Cu17.9Ni14.6 bulk metallic glass. Intermetallics 2002, 10, 1125–1129. [Google Scholar] [CrossRef]
- Wang, G.Y.; Liaw, P.K.; Peker, A.; Yang, B.; Benson, M.L.; Yuan, W.; Peter, W.H.; Huang, L.; Freels, M.; Buchanan, R.A.; et al. Fatigue behavior of Zr-Ti-Ni-Cu-Be bulk-metallic glasses. Intermetallics 2005, 13, 429–435. [Google Scholar] [CrossRef]
- Wang, G.Y.; Liaw, P.K.; Yokoyama, Y.; Inoue, A.; Liu, C.T. Fatigue behavior of Zr-based bulk-metallic glasses. Mater. Sci. Eng. A 2008, 494, 314–323. [Google Scholar] [CrossRef]
- Menzel, B.C.; Dauskardt, R.H. Stress-life fatigue behavior of a Zr-based bulk metallic glass. Acta Mater. 2006, 54, 935–943. [Google Scholar] [CrossRef]
- Freels, M.; Wang, G.Y.; Zhang, W.; Liaw, P.K.; Inoue, A. Cyclic compression behavior of a Cu-Zr-Al-Ag bulk metallic glass. Intermetallics 2011, 19, 1174–1183. [Google Scholar] [CrossRef]
- Wang, G.Y.; Liaw, P.K.; Yokoyama, Y.; Freels, M.; Inoue, A. The influence of Pd on tension-tension fatigue behavior of Zr-based bulk-metallic glasses. Int. J. Fatigue 2010, 32, 599–604. [Google Scholar] [CrossRef]
- Launey, M.E.; Busch, R.; Kruzic, J.J. Effects of free volume changes and residual stresses on the fatigue and fracture behavior of a Zr-Ti-Ni-Cu-Be bulk metallic glass. Acta Mater. 2008, 56, 500–510. [Google Scholar] [CrossRef]
- Fujita, K.; Zhang, W.; Shen, B.L.; Amiya, K.; Ma, C.L.; Nishiyama, N. Fatigue properties in high strength bulk metallic glasses. Intermetallics 2012, 30, 12–18. [Google Scholar] [CrossRef]
- Qiao, D.C.; Fan, G.J.; Liaw, P.K.; Choo, H. Fatigue behaviors of the Cu47.5Zr47.5Al5 bulk-metallic glass (BMG) and Cu47.5Zr38Hf9.5Al5 BMG composite. Int. J. Fatigue 2007, 29, 2149–2154. [Google Scholar] [CrossRef]
- Yue, Y.; Wang, R.; Ma, D.Q.; Tian, J.F.; Zhang, X.Y.; Jing, Q.; Ma, M.Z.; Liu, R.P. Fatigue behavior of a Zr-based bulk metallic glass under uniaxial tension–tension and three-point bending loading mode. Intermetallics 2015, 60, 86–91. [Google Scholar] [CrossRef]
- Morrison, M.L.; Buchanan, R.A.; Liaw, P.K.; Green, B.A.; Wang, G.Y.; Liu, C.T.; Horton, J.A. Four-point-bending-fatigue behavior of the Zr-based Vitreloy 105 bulk metallic glass. Mater. Sci. Eng. A 2007, 467, 190–197. [Google Scholar] [CrossRef]
- Jang, D.C.; Maaß, R.; Wang, G.Y.; Liaw, P.K.; Greer, J.R. Fatigue deformation of microsized metallic glasses. Scr. Mater. 2013, 68, 773–776. [Google Scholar] [CrossRef]
- Cameron, K.K.; Dauskardt, R.H. Fatigue damage in bulk metallic glass I: Simulation. Scr. Mater. 2006, 54, 349–353. [Google Scholar] [CrossRef]
- Lo, Y.C.; Chou, H.S.; Cheng, Y.T.; Huang, J.C.; Morris, J.R.; Liaw, P.K. Structural relaxation and self-repair behavior in nano-scaled Zr-Cu metallic glass under cyclic loading: Molecular dynamics simulations. Intermetallics 2010, 18, 954–960. [Google Scholar] [CrossRef]
- Sha, Z.D.; Qu, S.X.; Liu, Z.S.; Wang, T.J.; Gao, H. Cyclic deformation in metallic glasses. Nano Lett. 2015, 15, 7010–7015. [Google Scholar] [CrossRef] [PubMed]
- Spaepen, F. A microscopic mechanism for steady state inhomogeneous flow in metallic glasses. Acta Metall. 1976, 25, 407–415. [Google Scholar] [CrossRef]
- Steif, P.S.; Spaepen, F.; Hutchinson, J.W. Strain localization in amorphous metals. Acta Metall. 1982, 30, 447–455. [Google Scholar] [CrossRef]
- Gao, Y.F. An implicit finite element method for simulating inhomogeneous deformation and shear bands of amorphous alloys based on the free-volume model. Model. Simul. Mater. Sci. Eng. 2006, 14, 1329–1345. [Google Scholar] [CrossRef]
- Hibbit, Karlsson, Sorenson. ABAQUS Theory Manual; HKS inc.: Pawtucket, RI, USA, 2010. [Google Scholar]
- Huo, L.S.; Zeng, J.F.; Wang, W.H.; Liu, C.T.; Yang, Y. The dependence of shear modulus on dynamic relaxation and evolution of local structural heterogeneity in a metallic glass. Acta Mater. 2013, 61, 4329–4338. [Google Scholar] [CrossRef]
- Jiang, Y.P. Numerical study of the notch effect on the ductility of bulk metallic glasses (BMGs) based on the free-volume theory. J. Mater. Res. 2016, 31, 765–774. [Google Scholar] [CrossRef]
- Wang, X.D.; Qun, R.T.; Liu, Z.Q.; Zhang, Z.F. Shear band-mediated fatigue cracking mechanism of metallic glass at high stress level. Mater. Sci. Eng. A 2015, 627, 336–339. [Google Scholar] [CrossRef]
- Petrusenko, Yu.; Bakai, A.; Neklyudov, I.; Bakai, S.; Borysenko, V.; Wang, G.; Liaw, P.K.; Huang, L.; Zhang, T. Low- and high-frequency fatigue of bulk metallic glasses. J. Alloy. Compd. 2011, 509, S123–S127. [Google Scholar] [CrossRef]














© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y. Numerical Modeling of Cyclic Deformation in Bulk Metallic Glasses. Metals 2016, 6, 217. https://doi.org/10.3390/met6090217
Jiang Y. Numerical Modeling of Cyclic Deformation in Bulk Metallic Glasses. Metals. 2016; 6(9):217. https://doi.org/10.3390/met6090217
Chicago/Turabian StyleJiang, Yunpeng. 2016. "Numerical Modeling of Cyclic Deformation in Bulk Metallic Glasses" Metals 6, no. 9: 217. https://doi.org/10.3390/met6090217
APA StyleJiang, Y. (2016). Numerical Modeling of Cyclic Deformation in Bulk Metallic Glasses. Metals, 6(9), 217. https://doi.org/10.3390/met6090217