Modelling of the Superplastic Deformation of the Near-α Titanium Alloy (Ti-2.5Al-1.8Mn) Using Arrhenius-Type Constitutive Model and Artificial Neural Network
Abstract
:1. Introduction
2. Materials and Experiments
3. Test Results
4. Modeling Experiments
4.1. Arrhenius Constitutive Model (ACE)
4.1.1. Determination of the Arrhenius Constitutive Model Constants
4.1.2. Compensation of Strain Effect
4.1.3. Verification of the Arrhenius Constitutive Equations Model
4.2. Artificial Neural Network Analysis
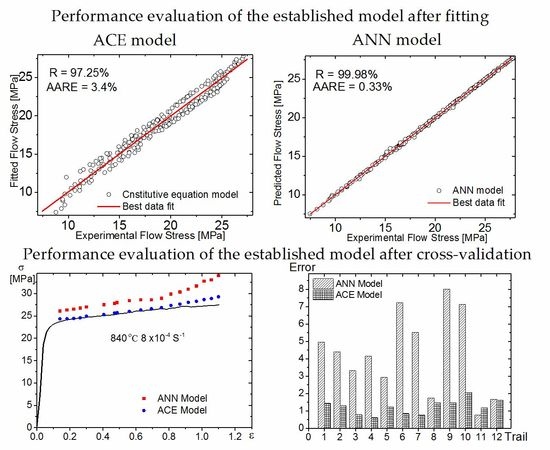
5. Cross-Validation of the Models
6. Conclusions
- (1)
- The values of α, n2, and A3 in the Arrhenius-type hyperbolic constitutive equation were found to be the function of strain in the studied strain rate–temperature–strain range. The material constant versus strain dependence suggested that, the symbiosis between the dislocation viscous glide and the grain boundary sliding are the deformation mechanisms.
- (2)
- The correlation coefficient (R), the mean absolute relative error (AARE) and the root mean square error (RMSE) obtained from the developed ACE and ANN are 95.25%, 5.2% and 1.09, respectively for the constitutive equations. In the case of ANN, the value of R, AARE and RMSE are 99.97%, 0.32% and 0.079 respectively. The ANN model exhibits higher accuracy and much better efficiency in approximating the hot deformation behaviour than the ACE at the points used for training in ANN.
- (3)
- Both models were verified by extracting the stress–strain experimental curves one by one, and comparing their predictability following the cross-validation approach. The ACE model exhibits better predictability of the superplastic deformation behavior as compared to the ANN model. An important outcome of this analysis is that, despite the rising popularity of the artificial neural networks, one should exercise caution when using them for predicting mechanical behaviour of materials. Cross-validation should be mandatory for such kind of ANN usage. In some cases, as shown in this work, the verification technique demonstrated that the classical approach based on the constitutive equations of Arrhenius type is more effective and reliable than the artificial neural networks.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Franciosi, P.; Berbenni, S. Heterogeneous crystal and poly-crystal plasticity modeling from a transformation field analysis within a regularized Schmid law. J. Mech. Phys. Solids 2007, 55, 2265–2299. [Google Scholar] [CrossRef]
- Sommitsch, C.; Sievert, R.; Wlanis, T.; Günther, B.; Wieser, V. Modelling of creep-fatigue in containers during aluminium and copper extrusion. Comput. Mater. Sci. 2007, 39, 55–64. [Google Scholar] [CrossRef]
- Dan, W.J.; Zhang, W.G.; Li, S.H.; Lin, Z.Q. A model for strain-induced martensitic transformation of TRIP steel with strain rate. Comput. Mater. Sci. 2007, 40, 101–107. [Google Scholar] [CrossRef]
- Haghdadi, N.; Zarei-Hanzaki, A.; Abedi, H.R. The flow behavior modeling of cast A356 aluminum alloy at elevated temperatures considering the effect of strain. Mater. Sci. Eng. A 2012, 535, 252–257. [Google Scholar] [CrossRef]
- Marandi, A.; Zarei-Hanzaki, A.; Haghdadi, N.; Eskandari, M. The prediction of hot deformation behavior in Fe-21Mn-2.5Si-1.5Al transformation-twinning induced plasticity steel. Mater. Sci. Eng. A 2012, 554, 72–78. [Google Scholar] [CrossRef]
- Zhang, H.; Wen, W.; Cui, H.; Xu, Y. A modified Zerilli-Armstrong model for alloy IC10 over a wide range of temperatures and strain rates. Mater. Sci. Eng. A 2009, 527, 328–333. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Almasri, A.H. A physically based constitutive model for fcc metals with applications to dynamic hardness. Mech. Mater. 2008, 40, 549–563. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, X.-M. A critical review of experimental results and constitutive descriptions for metals and alloys in hot working. Mater. Des. 2011, 32, 1733–1759. [Google Scholar] [CrossRef]
- Vanderhasten, M.; Rabet, L.; Verlinden, B. Ti–6Al–4V: Deformation map and modelisation of tensile behavior. Mater. Des. 2008, 29, 1090–1098. [Google Scholar] [CrossRef]
- Cai, J.; Li, F.; Liu, T.; Chen, B.; He, M. Constitutive equations for elevated temperature flow stress of Ti-6Al-4V alloy considering the effect of strain. Mater. Des. 2011, 32, 1144–1151. [Google Scholar] [CrossRef]
- Shafaat, M.A.; Omidvar, H.; Fallah, B. Prediction of hot compression flow curves of Ti-6Al-4V alloy in α+β phase region. Mater. Des. 2011, 32, 4689–4695. [Google Scholar] [CrossRef]
- Jonas, J.J.; Sellars, C.M.; Tegart, W.J.M. Strength and structure under hot-working conditions. Metall. Rev. 1969, 14, 1–24. [Google Scholar] [CrossRef]
- Bahrami, A.; Anijdan, S.H.M.; Hosseini, H.R.M.; Shafyei, A.; Narimani, R. Effective parameters modeling in compression of an austenitic stainless steel using artificial neural network. Comput. Mater. Sci. 2005, 34, 335–341. [Google Scholar] [CrossRef]
- Guo, Z.; Malinov, S.; Sha, W. Modelling beta transus temperature of titanium alloys using artificial neural network. Comput. Mater. Sci. 2005, 32, 1–12. [Google Scholar] [CrossRef]
- Malinov, S.; Sha, W. Application of artificial neural networks for modelling correlations in titanium alloys. Mater. Sci. Eng. A 2004, 365, 202–211. [Google Scholar] [CrossRef]
- Sun, Y.; Zeng, W.D.; Zhao, Y.Q.; Zhang, X.M.; Shu, Y.; Zhou, Y.G. Modeling constitutive relationship of Ti40 alloy using artificial neural network. Mater. Des. 2011, 32, 1537–1541. [Google Scholar] [CrossRef]
- Mandal, S.; Sivaprasad, P.V.; Venugopal, S. Capability of a Feed-Forward Artificial Neural Network to Predict the Constitutive Flow Behavior of As Cast 304 Stainless Steel Under Hot Deformation. J. Eng. Mater. Technol. 2006, 129, 242–247. [Google Scholar] [CrossRef]
- Qin, Y.J.; Pan, Q.L.; He, Y.B.; Li, W.B.; Liu, X.Y.; Fan, X. Artificial Neural Network Modeling to Evaluate and Predict the Deformation Behavior of ZK60 Magnesium Alloy During Hot Compression. Mater. Manuf. Process. 2010, 25, 539–545. [Google Scholar] [CrossRef]
- Reddy, N.S.; Lee, Y.H.; Park, C.H.; Lee, C.S. Prediction of flow stress in Ti-6Al-4V alloy with an equiaxed α+β microstructure by artificial neural networks. Mater. Sci. Eng. A 2008, 492, 276–282. [Google Scholar] [CrossRef]
- Mikhaylovskaya, A.V.; Mosleh, A.O.; Kotov, A.D.; Kwame, J.S.; Pourcelot, T.; Golovin, I.S.; Portnoy, V.K. Superplastic deformation behaviour and microstructure evolution of near-α Ti-Al-Mn alloy. Mater. Sci. Eng. A 2017, 708, 469–477. [Google Scholar] [CrossRef]
- Samantaray, D.; Mandal, S.; Bhaduri, A.K.; Sivaprasad, P.V. An overview on constitutive modelling to predict elevated temperature flow behaviour of fast reactor structural materials. Trans. Indian Inst. Met. 2010, 63, 823–831. [Google Scholar] [CrossRef]
- Zener, C.; Hollomon, J.H. Effect of Strain Rate Upon Plastic Flow of Steel. J. Appl. Phys. 1944, 15, 22–32. [Google Scholar] [CrossRef]
- Sellars, C.M.; McTegart, W.J. On the mechanism of hot deformation. Acta Metall. 1966, 14, 1136–1138. [Google Scholar] [CrossRef]
- Rao, K.P.; Hawbolt, E.B. Development of Constitutive Relationships Using Compression Testing of a Medium Carbon Steel. J. Eng. Mater. Technol. 1992, 114, 116–123. [Google Scholar] [CrossRef]
- Mandal, S.; Rakesh, V.; Sivaprasad, P.V.; Venugopal, S.; Kasiviswanathan, K.V. Constitutive equations to predict high temperature flow stress in a Ti-modified austenitic stainless steel. Mater. Sci. Eng. A 2009, 500, 114–121. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, M.-S.; Zhong, J. Constitutive modeling for elevated temperature flow behavior of 42CrMo steel. Comput. Mater. Sci. 2008, 42, 470–477. [Google Scholar] [CrossRef]
- Mahmudi, R.; Rezaee-Bazzaz, A.; Banaie-Fard, H.R. Investigation of stress exponent in the room-temperature creep of Sn-40Pb-2.5Sb solder alloy. J. Alloys Compd. 2007, 429, 192–197. [Google Scholar] [CrossRef]
- Langdon, T.G. Identifiying creep mechanisms at low stresses. Mater. Sci. Eng. A 2000, 283, 266–273. [Google Scholar] [CrossRef]
- Yang, X.; Guo, H.; Liang, H.; Yao, Z.; Yuan, S. Flow Behavior and Constitutive Equation of Ti-6.5Al-2Sn-4Zr-4Mo-1W-0.2Si Titanium Alloy. J. Mater. Eng. Perform. 2016, 25, 1347–1359. [Google Scholar] [CrossRef]
- Pu, Z.J.; Wu, K.H.; Shi, J.; Zou, D. Development of constitutive relationships for the hot deformation of boron microalloying TiAlCrV alloys. Mater. Sci. Eng. A 1995, 192–193, 780–787. [Google Scholar] [CrossRef]
- Weiss, I.; Semiatin, S.L. Thermomechanical processing of alpha titanium alloys—An overview. Mater. Sci. Eng. A 1999, 263, 243–256. [Google Scholar] [CrossRef]
- Frost, H.J.; Ashby, M.F. Deformation Mechanism Maps: The Plasticity and Creep of Metals and Ceramics, 1st ed.; Pergamon Press: New York, NY, USA, 1982; p. 166. ISBN 0080293379. [Google Scholar]
- Nieh, T.G.; Wadsworth, J.; Sherby, O.D. Superplasticity in Metals and Ceramics, 1st ed.; Cambridge University Press: Cambridge, UK, 1997; p. 288. ISBN 100521561051. [Google Scholar]
- Zhao, J.; Ding, H.; Zhao, W.; Huang, M.; Wei, D.; Jiang, Z. Modelling of the hot deformation behaviour of a titanium alloy using constitutive equations and artificial neural network. Comput. Mater. Sci. 2014, 92, 47–56. [Google Scholar] [CrossRef]
- Genel, K.; Kurnaz, S.C.; Durman, M. Modeling of tribological properties of alumina fiber reinforced zinc–aluminum composites using artificial neural network. Mater. Sci. Eng. A 2003, 363, 203–210. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Wu, S.W.; Zhou, X.G.; Cao, G.M.; Liu, Z.Y.; Wang, G.D. The improvement on constitutive modeling of Nb-Ti micro alloyed steel by using intelligent algorithms. Mater. Des. 2017, 116, 676–685. [Google Scholar] [CrossRef]
- Guo, L.F.; Li, B.C.; Xue, Y.; Zhang, Z.M. Constitutive Relationship Model of Al-W Alloy Using Artificial Neural Network. Adv. Mater. Res. 2014, 1004–1005, 1120–1124. [Google Scholar] [CrossRef]
- Ji, G.; Li, F.; Li, Q.; Li, H.; Li, Z. A comparative study on Arrhenius-type constitutive model and artificial neural network model to predict high-temperature deformation behaviour in Aermet100 steel. Mater. Sci. Eng. A 2011, 528, 4774–4782. [Google Scholar] [CrossRef]
- Sun, Y.; Zeng, W.D.; Zhao, Y.Q.; Qi, Y.L.; Ma, X.; Han, Y.F. Development of constitutive relationship model of Ti600 alloy using artificial neural network. Comput. Mater. Sci. 2010, 48, 686–691. [Google Scholar] [CrossRef]
- Peng, W.; Zeng, W.; Wang, Q.; Yu, H. Comparative study on constitutive relationship of as-cast Ti60 titanium alloy during hot deformation based on Arrhenius-type and artificial neural network models. Mater. Des. 2013, 51, 95–104. [Google Scholar] [CrossRef]
- Li, H.Y.; Wei, D.D.; Li, Y.H.; Wang, X.F. Application of artificial neural network and constitutive equations to describe the hot compressive behavior of 28CrMnMoV steel. Mater. Des. 2012, 35, 557–562. [Google Scholar] [CrossRef]
- Haghdadi, N.; Zarei-Hanzaki, A.; Khalesian, A.R.; Abedi, H.R. Artificial neural network modeling to predict the hot deformation behavior of an A356 aluminum alloy. Mater. Des. 2013, 49, 386–391. [Google Scholar] [CrossRef]
- Guo, L.; Li, B.; Zhang, Z. Constitutive relationship model of TC21 alloy based on artificial neural network. Trans. Nonferr. Met. Soc. China 2013, 23, 1761–1765. [Google Scholar] [CrossRef]









| ln(A1) | n1/m * | Q1 [KJ/mol] | ln(A2) | β [MPa−1] | Q2 [KJ/mol] | α | ln(A3) | n2 | Q3 [KJ/mol] |
|---|---|---|---|---|---|---|---|---|---|
| 14.6 | 2.8/0.35 | 287 ± 12 | 17.5 | 0.162 | 265 ± 10 | 0.057 | 21.5 | 2.166 | 279 ± 15 |
| Parameter | Y0 | B1 | B2 | B3 | B4 | B5 | R2 |
|---|---|---|---|---|---|---|---|
| Y10 = 0.077 | B11 = −0.135 | B12 = 0.363 | B13 = −0.55 | B14 = 0.387 | B15 = −0.096 | 0.998 | |
| Y20 = 1.19 | B21 = 2.99 | B22 = −1.57 | B23 = 0.48 | B24 = 2.193 | B25 = −2.58 | 0.995 | |
| Y30 = 33.17 | B31 = −137.03 | B32 = 621.85 | B33 = −1272 | B34 = 1112.9 | B35 = −348.2 | 0.997 | |
| Y40 = 384.76 | B41 = −1269.25 | B42 = 5751.1 | B43 = −11,719 | B44 = 10,220.4 | B45 = −3187 | 0.997 |
| Name of Network Parameters | Contents |
|---|---|
| Network | Back-Propagation |
| Training function | TrainLM |
| Performance function | MSE |
| Training epoch | 8000 |
| Goal | 1 × 10−6 |
| Transfer function of hidden layer | Tan-sigmoid |
| Transfer function of output | Liner (purelin) |
| Trial Number | Excluded Conditions | |
|---|---|---|
| Temperature (°C) | Strain Rate (s−1) | |
| Trial-1 | 840 | 2 × 10−4 |
| Trial-2 | 840 | 4 × 10−4 |
| Trial-3 | 840 | 8 × 10−4 |
| Trial-4 | 852 | 2 × 10−4 |
| Trial-5 | 852 | 4 × 10−4 |
| Trial-6 | 852 | 8 × 10−4 |
| Trial-7 | 865 | 2 × 10−4 |
| Trial-8 | 865 | 4 × 10−4 |
| Trial-9 | 865 | 8 × 10−4 |
| Trial-10 | 890 | 2 × 10−4 |
| Trial-11 | 890 | 4 × 10−4 |
| Trial-12 | 890 | 8 × 10−4 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mosleh, A.; Mikhaylovskaya, A.; Kotov, A.; Pourcelot, T.; Aksenov, S.; Kwame, J.; Portnoy, V. Modelling of the Superplastic Deformation of the Near-α Titanium Alloy (Ti-2.5Al-1.8Mn) Using Arrhenius-Type Constitutive Model and Artificial Neural Network. Metals 2017, 7, 568. https://doi.org/10.3390/met7120568
Mosleh A, Mikhaylovskaya A, Kotov A, Pourcelot T, Aksenov S, Kwame J, Portnoy V. Modelling of the Superplastic Deformation of the Near-α Titanium Alloy (Ti-2.5Al-1.8Mn) Using Arrhenius-Type Constitutive Model and Artificial Neural Network. Metals. 2017; 7(12):568. https://doi.org/10.3390/met7120568
Chicago/Turabian StyleMosleh, Ahmed, Anastasia Mikhaylovskaya, Anton Kotov, Theo Pourcelot, Sergey Aksenov, James Kwame, and Vladimir Portnoy. 2017. "Modelling of the Superplastic Deformation of the Near-α Titanium Alloy (Ti-2.5Al-1.8Mn) Using Arrhenius-Type Constitutive Model and Artificial Neural Network" Metals 7, no. 12: 568. https://doi.org/10.3390/met7120568
APA StyleMosleh, A., Mikhaylovskaya, A., Kotov, A., Pourcelot, T., Aksenov, S., Kwame, J., & Portnoy, V. (2017). Modelling of the Superplastic Deformation of the Near-α Titanium Alloy (Ti-2.5Al-1.8Mn) Using Arrhenius-Type Constitutive Model and Artificial Neural Network. Metals, 7(12), 568. https://doi.org/10.3390/met7120568