Strain Localization during Equal-Channel Angular Pressing Analyzed by Finite Element Simulations
Abstract
:1. Introduction
2. Simulation Model
- A two-dimensional plane-strain simulation is used. Therefore, boundary effects perpendicular to the simulated plane have to be neglected. The main reason for this simplification is the computational effort, which increases excessively when changing to a three-dimensional model. However, the comparison of simulation and experimental results (Section 3) demonstrates that the error of this simplification is small.
- As the investigation of viscous effects goes beyond the scope of this study, a rate-independent model was chosen. The aluminum material used in the experimental studies exhibits only a minor rate dependence and the experiments have been performed at room temperature. Due to the very low pressing speed of 0.3 mm/s and consequently low strain rates inside the shear zone, the error of this limitation is kept small. Furthermore, adiabatic heating phenomena are essentially negligible and do not have any practical significance [39].
- A frictionless model was used to simulate ECAP. In the experimental studies, the ECAP die is always lubricated such that the friction coefficient is low [40]. In addition, both in the experiments and in the simulations, the exit channel is moved with the billet in order to minimize the friction [41]. Because of this, self-heating due to friction may be neglected.
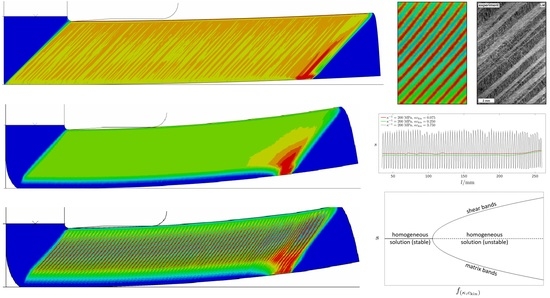
3. Parameter Variation
3.1. Reference Simulation
3.2. Effects of Isotropic Hardening
3.3. Effects of Kinematic Hardening
3.4. Experimental Validation
4. Remarks on the Mechanism of Heterogeneous Plastic Flow
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| ECAP | equal-channel angular pressing |
| SPD | severe plastic deformation |
| IHR | initial hardening rate |
| SHC | strain hardening capacity |
| EBSD | electron back-scatter diffraction |
| KKT | Karush–Kuhn–Tucker |
| FE | finite element |
References
- Segal, V. The Method of Material Preparation for Subsequent Working. Patent of the USSR Nr. 575892, 1977. [Google Scholar]
- Segal, V.; Reznikov, V.; Dobryshevshiy, A.; Kopylov, V. Plastic working of metals by simple shear. Russ. Metall. (Metally) 1981, 1, 99–105. [Google Scholar]
- Iwahashi, Y.; Wang, J.; Horita, Z.; Nemoto, M.; Langdon, T.G. Principle of equal-channel angular pressing for the processing of ultra-fine grained materials. Scr. Mater. 1996, 35, 143–146. [Google Scholar] [CrossRef]
- Hall, E. The deformation and ageing of mild steel: III discussion of results. Proc. Phys. Soc. Sect. B 1951, 64, 747. [Google Scholar] [CrossRef]
- Petch, N. The cleavage strength of polycrystals. J. Iron Steel Inst. 1953, 174, 25–28. [Google Scholar]
- Valiev, R.; Alexandrov, I.; Zhu, Y.; Lowe, T. Paradox of strength and ductility in metals processed bysevere plastic deformation. J. Mater. Res. 2002, 17, 5–8. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, M.; Zhou, F.; Ma, E. High tensile ductility in a nanostructured metal. Nature 2002, 419, 912–915. [Google Scholar] [CrossRef] [PubMed]
- Ma, A.; Jiang, J.; Saito, N.; Shigematsu, I.; Yuan, Y.; Yang, D.; Nishida, Y. Improving both strength and ductility of a Mg alloy through a large number of ECAP passes. Mater. Sci. Eng. A 2009, 513, 122–127. [Google Scholar] [CrossRef]
- Valiev, R.Z.; Langdon, T.G. Principles of equal-channel angular pressing as a processing tool for grain refinement. Prog. Mater. Sci. 2006, 51, 881–981. [Google Scholar] [CrossRef]
- Kim, W.; Chung, C.; Ma, D.; Hong, S.; Kim, H. Optimization of strength and ductility of 2024 Al by equal channel angular pressing (ECAP) and post-ECAP aging. Scr. Mater. 2003, 49, 333–338. [Google Scholar] [CrossRef]
- Frint, P. Lokalisierungsphänomene Nach Kombinierter Hochgradig Plastischer Umformung Durch Extrusion und ECAP Einer 6000er-Aluminiumlegierung. Ph.D. Thesis, Chemnitz University of Technology, Chemnitz, Germany, 2015. [Google Scholar]
- Lapovok, R.; Tóth, L.S.; Molinari, A.; Estrin, Y. Strain localisation patterns under equal-channel angular pressing. J. Mech. Phys. Solids 2009, 57, 122–136. [Google Scholar] [CrossRef]
- Zhilyaev, A.; Swisher, D.; Oh-Ishi, K.; Langdon, T.; McNelley, T. Microtexture and microstructure evolution during processing of pure aluminum by repetitive ECAP. Mater. Sci. Eng. A 2006, 429, 137–148. [Google Scholar] [CrossRef] [Green Version]
- Segal, V. Equal channel angular extrusion: from macromechanics to structure formation. Mater. Sci. Eng. A 1999, 271, 322–333. [Google Scholar] [CrossRef]
- Miyamoto, H.; Ikeda, T.; Uenoya, T.; Vinogradov, A.; Hashimoto, S. Reversible nature of shear bands in copper single crystals subjected to iterative shear of ECAP in forward and reverse directions. Mater. Sci. Eng. A 2011, 528, 2602–2609. [Google Scholar] [CrossRef]
- Prangnell, P.; Harris, C.; Roberts, S. Finite element modelling of equal channel angular extrusion. Scr. Mater. 1997, 37, 983–989. [Google Scholar] [CrossRef]
- Raab, G. Plastic flow at equal channel angular processing in parallel channels. Mater. Sci. Eng. A 2005, 410, 230–233. [Google Scholar] [CrossRef]
- Dumoulin, S.; Roven, H.; Werenskiold, J.; Valberg, H. Finite element modeling of equal channel angular pressing: Effect of material properties, friction and die geometry. Mater. Sci. Eng. A 2005, 410, 248–251. [Google Scholar] [CrossRef]
- Kim, H.S.; Seo, M.H.; Hong, S.I. Finite element analysis of equal channel angular pressing of strain rate sensitive metals. J. Mater. Process. Technol. 2002, 130, 497–503. [Google Scholar] [CrossRef]
- Yoon, S.C.; Kim, H.S. Finite element analysis of the effect of the inner corner angle in equal channel angular pressing. Mater. Sci. Eng. A 2008, 490, 438–444. [Google Scholar] [CrossRef]
- Kim, H.S.; Seo, M.H.; Hong, S.I. Plastic deformation analysis of metals during equal channel angular pressing. J. Mater. Process. Technol. 2001, 113, 622–626. [Google Scholar] [CrossRef]
- Park, J.W.; Suh, J.Y. Effect of die shape on the deformation behavior in equal-channel angular pressing. Metall. Mater. Trans. A 2001, 32, 3007–3014. [Google Scholar] [CrossRef]
- Li, S.; Bourke, M.; Beyerlein, I.; Alexander, D.; Clausen, B. Finite element analysis of the plastic deformation zone and working load in equal channel angular extrusion. Mater. Sci. Eng. A 2004, 382, 217–236. [Google Scholar] [CrossRef]
- Figueiredo, R.B.; Cetlin, P.R.; Langdon, T.G. Stable and unstable flow in materials processed by equal-channel angular pressing with an emphasis on magnesium alloys. Metall. Mater. Trans. A 2010, 41, 778–786. [Google Scholar] [CrossRef]
- Semiatin, S.; Delo, D.; Shell, E. The effect of material properties and tooling design on deformation and fracture during equal channel angular extrusion. Acta Mater. 2000, 48, 1841–1851. [Google Scholar] [CrossRef]
- Oruganti, R.; Subramanian, P.; Marte, J.; Gigliotti, M.F.; Amancherla, S. Effect of friction, backpressure and strain rate sensitivity on material flow during equal channel angular extrusion. Mater. Sci. Eng. A 2005, 406, 102–109. [Google Scholar] [CrossRef]
- Bowen, J.; Gholinia, A.; Roberts, S.; Prangnell, P. Analysis of the billet deformation behaviour in equal channel angular extrusion. Mater. Sci. Eng. A 2000, 287, 87–99. [Google Scholar] [CrossRef]
- Figueiredo, R.B.; Aguilar, M.T.P.; Cetlin, P.R. Finite element modelling of plastic instability during ECAP processing of flow-softening materials. Mater. Sci. Eng. A 2006, 430, 179–184. [Google Scholar] [CrossRef]
- Ghazani, M.S.; Vajd, A. Finite Element Simulation of Flow Localization During Equal Channel Angular Pressing. Trans. Indian Inst. Met. 2017, 70, 1323–1328. [Google Scholar] [CrossRef]
- Shutov, A.; Kreißig, R. Finite strain viscoplasticity with nonlinear kinematic hardening: Phenomenological modeling and time integration. Comput. Methods Appl. Mech. Eng. 2008, 197, 2015–2029. [Google Scholar] [CrossRef]
- Kießling, R.; Landgraf, R.; Scherzer, R.; Ihlemann, J. Introducing the concept of directly connected rheological elements by reviewing rheological models at large strains. Int. J. Solids Struct. 2016, 97, 650–667. [Google Scholar] [CrossRef]
- Frederick, C.O.; Armstrong, P. A mathematical representation of the multiaxial Bauschinger effect. Mater. High Temp. 2014, 24, 1–26. [Google Scholar] [CrossRef]
- Voce, E. The relationship between stress and strain for homogeneous deformation. J. Inst. Met. 1948, 74, 537–562. [Google Scholar]
- Perzyna, P. The constitutive equations for rate sensitive plastic materials. Q. Appl. Math. 1963, 20, 321–332. [Google Scholar] [CrossRef]
- Horn, T. Simulation und FE-Analyse der Verformungslokalisierung bei der ECAP-Umformung. Master’s Thesis, Chemnitz University of Technology, Chemnitz, Germany, 2016. [Google Scholar]
- Shutov, A.V.; Kreißig, R. Geometric integrators for multiplicative viscoplasticity: Analysis of error accumulation. Comput. Methods Appl. Mech. Eng. 2010, 199, 700–711. [Google Scholar] [CrossRef]
- Shutov, A.V.; Kuprin, C.; Ihlemann, J.; Wagner, M.F.X.; Silbermann, C. Experimentelle Untersuchung und numerische Simulation des inkrementellen Umformverhaltens von Stahl 42CrMo4 Experimental investigation and numerical simulation of the incremental deformation of a 42CrMo4 steel. Materialwissenschaft Werkstofftechnik 2010, 41, 765–775. [Google Scholar] [CrossRef]
- Silbermann, C.B.; Shutov, A.V.; Ihlemann, J. On operator split technique for the time integration within finite strain viscoplasticity in explicit FEM. PAMM 2014, 14, 355–356. [Google Scholar] [CrossRef]
- Yamaguchi, D.; Horita, Z.; Nemoto, M.; Langdon, T.G. Significance of adiabatic heating in equal-channel angular pressing. Scr. Mater. 1999, 41, 791–796. [Google Scholar] [CrossRef]
- Frint, P.; Wagner, M.F.X.; Weber, S.; Seipp, S.; Frint, S.; Lampke, T. An experimental study on optimum lubrication for large-scale severe plastic deformation of aluminum-based alloys. J. Mater. Process. Technol. 2017, 239, 222–229. [Google Scholar] [CrossRef]
- Frint, S.; Hockauf, M.; Frint, P.; Wagner, M.F.X. Scaling up Segal’s principle of Equal-Channel Angular Pressing. Mater. Des. 2016, 97, 502–511. [Google Scholar] [CrossRef]
- Horn, T.; Silbermann, C.; Ihlemann, J. FE-Simulation based analysis of residual stresses and strain localizations in ECAP processing. PAMM 2017, 16. in press. [Google Scholar]
- Frint, P.; Hockauf, M.; Dietrich, D.; Halle, T.; Wagner, M.F.X.; Lampke, T. Influence of strain gradients on the grain refinement during industrial scale ECAP. Materialwissenschaft Werkstofftechnik 2011, 42, 680–685. [Google Scholar] [CrossRef]
- Frint, P.; Hockauf, M.; Halle, T.; Wagner, M.F.X.; Lampke, T. The role of backpressure during large scale Equal-Channel Angular Pressing. Materialwissenschaft Werkstofftechnik 2012, 43, 668–672. [Google Scholar] [CrossRef]
- Frint, P.; Hockauf, M.; Halle, T.; Strehl, G.; Lampke, T.; Wagner, M.F.X. Microstructural Features and Mechanical Properties after Industrial Scale ECAP of an Al 6060 Alloy. Mater. Sci. Forum 2011, 667, 1153–1158. [Google Scholar] [CrossRef]
- Lefstad, M.; Pedersen, K.; Dumoulin, S. Up-scaled equal channel angular pressing of AA6060 and subsequent mechanical properties. Mater. Sci. Eng. A 2012, 535, 235–240. [Google Scholar] [CrossRef]
- Chaudhury, P.K.; Cherukuri, B.; Srinivasan, R. Scaling up of equal-channel angular pressing and its effect on mechanical properties, microstructure, and hot workability of AA 6061. Mater. Sci. Eng. A 2005, 410, 316–318. [Google Scholar] [CrossRef]
- Berndt, N.; Frint, P.; Böhme, M.; Wagner, M.F.X. Microstructure and mechanical properties of an AA6060 aluminum alloy after cold and warm extrusion. Mater. Sci. Eng. A 2017, 707, 717–724. [Google Scholar] [CrossRef]
- Beyerlein, I.J.; Tomé, C.N. Analytical modeling of material flow in equal channel angular extrusion (ECAE). Mater. Sci. Eng. A 2004, 380, 171–190. [Google Scholar] [CrossRef]
- Ebeling, W.; Feistel, R. Chaos und Kosmos: Prinzipien der Evolution; Spektrum Akad. Verlag: Heidelberg, Germany, 1994; pp. 109–118. [Google Scholar]
- Ebeling, W. Chaos, Ordnung und Information: Selbstorganisation in Natur und Technik; Urania-Verlag: Leipzig, Germany, 1989; Volume 74, p. 40. [Google Scholar]

















| Φ | Ψ | R | d | h | |||||
|---|---|---|---|---|---|---|---|---|---|
| 50 mm | 52 mm | 300 mm | 300 mm | 75 mm | 5 mm | 41 mm |
 |
| K/MPa | G/MPa | /MPa | /MPa | /MPa | ||
|---|---|---|---|---|---|---|
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Horn, T.D.; Silbermann, C.B.; Frint, P.; Wagner, M.F.-X.; Ihlemann, J. Strain Localization during Equal-Channel Angular Pressing Analyzed by Finite Element Simulations. Metals 2018, 8, 55. https://doi.org/10.3390/met8010055
Horn TD, Silbermann CB, Frint P, Wagner MF-X, Ihlemann J. Strain Localization during Equal-Channel Angular Pressing Analyzed by Finite Element Simulations. Metals. 2018; 8(1):55. https://doi.org/10.3390/met8010055
Chicago/Turabian StyleHorn, Tobias Daniel, Christian Bert Silbermann, Philipp Frint, Martin Franz-Xaver Wagner, and Jörn Ihlemann. 2018. "Strain Localization during Equal-Channel Angular Pressing Analyzed by Finite Element Simulations" Metals 8, no. 1: 55. https://doi.org/10.3390/met8010055
APA StyleHorn, T. D., Silbermann, C. B., Frint, P., Wagner, M. F.-X., & Ihlemann, J. (2018). Strain Localization during Equal-Channel Angular Pressing Analyzed by Finite Element Simulations. Metals, 8(1), 55. https://doi.org/10.3390/met8010055