Modeling of Precipitation Hardening during Coiling of Nb–Mo Steels
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
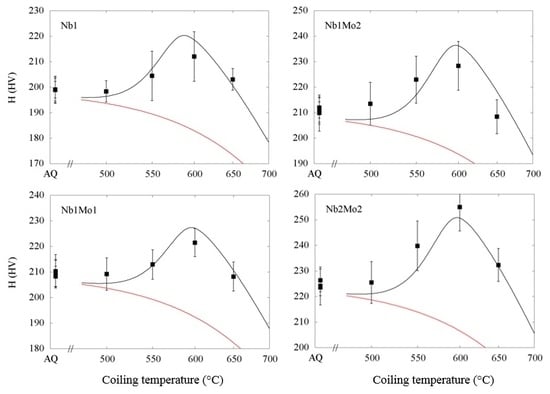
3.1. Age Hardening Results
3.1.1. Hardness Kinetics
3.1.2. Microstructure
3.2. Modeling
3.2.1. Time-Temperature Equivalence
3.2.2. Tempering
3.2.3. Precipitation Strengthening Model
3.3. Coiling Simulations
3.3.1. Microstructure
3.3.2. Transformation Hardening
3.3.3. Model Validation
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gladman, T. The Physical Metallurgy of Microalloyed Steels, 1st ed.; Institute of Materials: London, UK, 1997. [Google Scholar]
- Bouaziz, O.; Zurob, H.; Huang, M. Driving force and logic of development of advanced high strength steels for automotive applications. Steel Res. Int. 2013, 84, 937–947. [Google Scholar] [CrossRef]
- Kim, Y.M.; Kim, S.K.; Lim, Y.J.; Kim, N.J. Effect of microstructure on the yield ratio and low temperature toughness of linepipe steels. ISIJ Int. 2002, 42, 1571–1577. [Google Scholar] [CrossRef]
- Militzer, M.; Hawbolt, E.B.; Meadowcroft, T.R. Microstructural model for hot strip rolling of high-strength low-alloy steels. Metall. Mater. Trans. 2000, 31, 1247–1259. [Google Scholar] [CrossRef]
- Militzer, M.; Poole, W.J.; Sun, W. Precipitation hardening of HSLA steels. Steel Res. 1998, 69, 279–285. [Google Scholar] [CrossRef]
- Matlock, D.K.; Speer, J.G.; De Moor, E.; Gibbs, P.J. Recent developments in advanced high strength sheet steels for automotive applications: An overview. JEStech 2012, 15, 1–12. [Google Scholar]
- Mohrbacher, H.; Sun, X.; Yong, Q.; Dong, H. MoNb-based alloying concepts for low-carbon bainitic steels. In Advanced Steels: The Recent Scenario in Steel Science and Technology; Weng, Y., Dong, H., Gan, Y., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 289–302. [Google Scholar]
- Lee, W.-B.; Hong, S.-G.; Park, C.-G.; Park, S.-H. Carbide precipitation and high-temperature strength of hot-rolled high-strength low-alloy steels containing Nb and Mo. Metall. Mater. Trans. A 2002, 33, 1689–1698. [Google Scholar] [CrossRef]
- Huang, B.M.; Yang, J.R.; Yen, H.W.; Hsu, C.H.; Huang, C.Y.; Mohrbacher, H. Secondary hardened bainite. Mater. Sci. Technol. 2014, 30, 1014–1023. [Google Scholar] [CrossRef]
- Isasti, N.; Jorge-Badiola, D.; Taheri, M.L.; Uranga, P. Microstructural features controlling mechanical properties in Nb–Momicroalloyed steels. Part I: yield strength. Metall. Mater. Trans. A 2014, 45, 4960–4971. [Google Scholar] [CrossRef]
- Dutta, B.; Palmiere, E.J.; Sellars, C.M. Modelling the kinetics of strain-induced precipitation in Nb microalloyed steels. Acta. Mater 2001, 49, 785–794. [Google Scholar] [CrossRef]
- Fernandez, A.I.; Uranga, P.; Lopez, B.; Rodriguez-Ibabe, J.M. Dynamic recrystallization behavior covering a wide austenite grain size range in Nb and Nb–Ti microalloyed steels. Mater. Sci. Eng. A 2003, 361, 367–376. [Google Scholar] [CrossRef]
- Hutchinson, C.R.; Zurob, H.S.; Sinclair, C.W.; Brechet, Y.J.M. The comparative effectiveness of Nb solute and NbC precipitates at impeding grain-boundary motion in Nb steels. Scr. Mater. 2008, 59, 635–637. [Google Scholar] [CrossRef]
- Uemori, R.; Chijiiwa, R.; Tamehiro, H.; Morikawa, H. AP-FIM study on the effect of Mo addition on microstructure in Ti-Nb steel. Appl. Surf. Sci. 1994, 76–77, 255–260. [Google Scholar] [CrossRef]
- Charleux, M.; Poole, W.J.; Militzer, M.; Deschamps, A. Precipitation behavior and its effect on strengthening of an HSLA-Nb/Ti steel. Metall. Mater. Trans. A 2001, 32, 1635–1647. [Google Scholar] [CrossRef]
- Perrard, F.; Deschamps, A.; Maugis, P. Modelling the precipitation of NbC on dislocations in α-Fe. Acta Mater. 2007, 55, 1255–1266. [Google Scholar] [CrossRef] [Green Version]
- Maetz, J.-Y.; Militzer, M.; Goo, N.H.; Kim, S.J.; Jian, B.; Mohrbacher, H. Modelling of precipitation hardening in Nb–Molow carbon steels. In Proceedings of the Thermomechanical Processing (TMP) Conference, Milan, Italy, 26–28 October 2016. [Google Scholar]
- Maetz, J.-Y.; Militzer, M.; Chen, H.Y.W.; Yang, J.R.; Goo, N.H.; Kim, S.J.; Jian, B.; Mohrbacher, H. Modeling of age hardening kinetics during coiling of high performance Nb–Mosteels. In Proceedings of the International Symposium on New Developments in Advanced High-Strength Sheets steels, Warrendale, PA, USA, 30 May–2 June 2017. [Google Scholar]
- Hall, D.; Worobec, J. Torsion simulation of the hot strip rolling process. In Phase Transformations during the Thermal/Mechanical Processing of Steel, Proceedings of 34th Annual Conference of Metallurgists of CIM, Vancouver, BC, Canada, 20–24 August 1995; Canadian Institute of Mining, Metallurgy and Petroleum: Westmount, QC, Canada, 1995; pp. 305–316. [Google Scholar]
- Iza-Mendia, A.; Gutiérrez, I. Generalization of the existing relations between microstructure and yield stress from ferrite-pearlite to high strength steels. Mater. Sci. Eng. A 2013, 561, 40–51. [Google Scholar] [CrossRef]
- Reichert, J. Structure and properties of complex transformation products in Nb/Mo-microalloyed steels. Ph.D. Thesis, The University of British Columbia, Vancouver, BC, Canada, April 2016. [Google Scholar]
- Calcagnotto, M.; Ponge, D.; Demir, E.; Raabe, D. Orientation gradients and geometrically necessary dislocations in ultrafine grained dual-phase steels studied by 2D and 3D EBSD. Mater. Sci. Eng. A 2010, 527, 2738–2746. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Sun, X.J.; Yong, Q.L.; Li, Z.D.; Wang, Z.Q.; Wang, G.D. Precipitation behavior of nanometer-sized carbides in Nb–Momicroalloyed high strength steel and its strengthening mechanism. Acta Metall. Sin. 2016, 52, 410. [Google Scholar]
- Mehrer, H. Landolt-Börnstein—Group III Condensed Matter; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar]
- Choquet, P.; Fabregue, P.; Guisti, J.; Chamont, B.; Pezant, J.N.; Blancet, F. Modelling of forces, structure and final properties during the hot rolling process on the hot strip mill. In Mathematical Modelling of Hot Rolling of Steel; Canadian Institute of Mining and Metallurgy: Montreal, QC, Canada, August 1990; pp. 34–43. [Google Scholar]
- Pickering, F.B.; Gladman, T. Metallurgical Developments in Carbon Steels; Iron and Steel Institute: London, UK, 1963. [Google Scholar]
- Hansen, N. Hall-Petch relation and boundary strengthening. Scr. Mater. 2004, 51, 801–806. [Google Scholar] [CrossRef]
- Brewer, L.N.; Field, D.P.; Merriman, C.C. Mapping and assessing plastic deformation using EBSD. In Electron Backscatter Diffraction in Materials Science, 2nd ed.; Schwartz, A.J., Kumar, M., Adams, B.L., Field, D.P., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; p. 251. [Google Scholar]
- Ashby, M.F.; Jones, D.R.H. Engineering Materials 2, 3rd ed.; Pergamon: Oxford, UK; Burlington, MA, USA, 1980. [Google Scholar]
- Zhang, P.; Li, S.X.; Zhang, Z.F. General relationship between strength and hardness. Mater. Sci. Eng. A 2011, 529, 62–73. [Google Scholar] [CrossRef]
- Zhang, Z.; Delagnes, D.; Bernhart, G. Microstructure evolution of hot-work tool steels during tempering and definition of a kinetic law based on hardness measurements. Mater. Sci. Eng. A 2004, 380, 222–230. [Google Scholar] [CrossRef]
- Shercliff, H.R.; Ashby, M.F. A process model for age hardening of aluminium alloys—I. The model. Acta Metall. Mater. 1990, 38, 1789–1802. [Google Scholar] [CrossRef]
- Sarkar, S.; Militzer, M. Microstructure evolution model for hot strip rolling of Nb–Mo microalloyed complex phase steel. Mater. Sci. Technol. 2009, 25, 1134–1146. [Google Scholar] [CrossRef]


















| Steel | C | Mn | Si | Nb | Mo |
|---|---|---|---|---|---|
| Nb1 | 0.08 | 1.5 | 0.2 | 0.05 | 0 |
| Nb1Mo1 | 0.08 | 1.5 | 0.2 | 0.05 | 0.1 |
| Nb1Mo2 | 0.08 | 1.5 | 0.2 | 0.05 | 0.2 |
| Nb2Mo2 | 0.08 | 1.5 | 0.2 | 0.1 | 0.2 |
| Pass | R1–R3 | F1 | F2 | F3 | F4 | F5 | F6 | F7 |
|---|---|---|---|---|---|---|---|---|
| Temperature (°C) | 1100 | 1024 | 982 | 958 | 950 | 922 | 910 | 900 |
| Strain (1 s−1 rate) | 0.33 each | 0.35 | 0.5 | 0.4 | 0.3 | 0.3 | 0.3 | 0.1 |
| Interpass time (s) | 10 | 4 | 2.4 | 1.6 | 1.2 | 0.8 | 0.6 | - |
| Steel | Nb1 | Nb1Mo1 | Nb1Mo2 | Nb2Mo2 |
|---|---|---|---|---|
| EQAD (>2°) (µm) | 2.6 | 2.4 | 2.2 | 1.9 |
| LAGB density (mm−1) | 191 | 282 | 335 | 392 |
| Mean KAM (<2°) | 0.48 | 0.55 | 0.60 | 0.62 |
| M/A fraction (%) | 3.1 | 3.5 | 3.5 | 3.9 |
| Steel | Coiling Temperature (°C) | M/A Fraction (%, ±0.5) | Mean KAM (°, ±0.05) | EQAD2° (µm, ±0.1) |
|---|---|---|---|---|
| Nb1 | 500 | 0 | 0.51 | 2.7 |
| 550 | 0 | 0.41 | 2.9 | |
| 600 | 0.3 | 0.42 | 3.0 | |
| 650 | 0 | 0.40 | 3.4 | |
| Nb1Mo1 | 600 | 0.3 | 0.47 | 2.9 |
| Nb1Mo2 | 500 | 0.4 | 0.59 | 2.4 |
| 550 | 1.0 | 0.55 | 2.4 | |
| 600 | 2.1 | 0.48 | 2.5 | |
| 650 | 0.7 | 0.40 | 3.2 | |
| Nb2Mo2 | 600 | 2.1 | 0.56 | 2.3 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maetz, J.-Y.; Militzer, M.; Chen, Y.W.; Yang, J.-R.; Goo, N.H.; Kim, S.J.; Jian, B.; Mohrbacher, H. Modeling of Precipitation Hardening during Coiling of Nb–Mo Steels. Metals 2018, 8, 758. https://doi.org/10.3390/met8100758
Maetz J-Y, Militzer M, Chen YW, Yang J-R, Goo NH, Kim SJ, Jian B, Mohrbacher H. Modeling of Precipitation Hardening during Coiling of Nb–Mo Steels. Metals. 2018; 8(10):758. https://doi.org/10.3390/met8100758
Chicago/Turabian StyleMaetz, Jean-Yves, Matthias Militzer, Yu Wen Chen, Jer-Ren Yang, Nam Hoon Goo, Soo Jin Kim, Bian Jian, and Hardy Mohrbacher. 2018. "Modeling of Precipitation Hardening during Coiling of Nb–Mo Steels" Metals 8, no. 10: 758. https://doi.org/10.3390/met8100758
APA StyleMaetz, J. -Y., Militzer, M., Chen, Y. W., Yang, J. -R., Goo, N. H., Kim, S. J., Jian, B., & Mohrbacher, H. (2018). Modeling of Precipitation Hardening during Coiling of Nb–Mo Steels. Metals, 8(10), 758. https://doi.org/10.3390/met8100758