A Study on the Nanoparticles Evolution in Isothermally Aged Strain Glass of Ti48.7Ni51.3 Shape Memory Alloy by In Situ Small-Angle X-ray Scattering
Abstract
:1. Introduction
2. Materials and Methods
3. Results
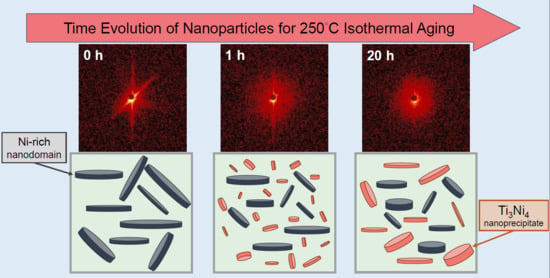
3.1. Formation and Structural Evolution of the New Nanoprecipitates during Isothermal Aging at 250 °C
3.2. Structural Evolution of Ni-Rich Nanodomains during Isothermal Aging at 250 °C
3.3. Variation of Strain Glass Temperature Tg and Frequency-Dependent Storage Modulus E0 with Aging Time at 250 °C
4. Discussion
4.1. Concurrent Phase Evolutions and Kinetics of Ni-Rich Nanodomains and Ti3Ni4 Nanoprecipitates
4.1.1. Precipitation Kinetics and Mechanism of Ti3Ni4 Nanoprecipitates
4.1.2. Dissolution Kinetics and Mechanism of Ni-Rich Nanodomains
4.2. Role and Quantitative Correlation of Ni-Rich Nanodomains and Ti3Ni4 Nanoprecipitates to the Loss of Strain Glass Characteristic
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Otsuka, K.; Shimizu, K. Pseudoelasticity and shape memory effects in alloys. Int. Met. Rev. 1986, 31, 93–114. [Google Scholar] [CrossRef]
- Otsuka, K.; Wayman, C.M. Shape Memory Materials; Cambridge University Press: Cambridge, UK, 1999; pp. 1–96. [Google Scholar]
- Otsuka, K.; Ren, X. Physical metallurgy of Ti-Ni-based shape memory alloys. Prog. Mater. Sci. 2005, 50, 511–678. [Google Scholar] [CrossRef]
- Sarkar, S.; Ren, X.B.; Otsuka, K. Evidence for strain glass in the ferroelastic-martensitic system Ti50−xNi50+x. Phys. Rev. Lett. 2005, 95, 205702. [Google Scholar] [CrossRef] [PubMed]
- Ren, X.B.; Wang, Y.; Otsuka, K.; Lloveras, P.; Castan, T.; Porta, M.; Planes, A.; Saxena, A. Ferroelastic nanostructures and nanoscale transitions: Ferroics with point defects. MRS Bull. 2009, 34, 838–846. [Google Scholar] [CrossRef]
- Vasseur, R.; Lookman, T. Effects of disorder in ferroelastics: A spin model for strain glass. Phys. Rev. B 2010, 81, 094107. [Google Scholar] [CrossRef]
- Ren, X.B.; Wang, Y.; Zhou, Y.M.; Zhang, Z.; Wang, D.; Fan, G.L.; Otsuka, K.; Suzuki, T.; Ji, Y.C.; Zhang, J.; et al. Strain glass in ferroelastic systems: Premartensitic tweed versus strain glass. Philos. Mag. 2010, 90, 141–157. [Google Scholar] [CrossRef]
- Wang, D.; Wang, Y.Z.; Zhang, Z.; Ren, X.B. Modeling abnormal strain states in ferroelastic systems: The role of point defects. Phys. Rev. Lett. 2010, 105, 205702–205704. [Google Scholar] [CrossRef] [PubMed]
- Ren, X.B. Strain glass and strain glass transition. In Disorder and Strain-Induced Complexity in Functional Materials; Springer: Berlin/Heidelberg, Germany, 2012; pp. 201–225. [Google Scholar]
- Vugmeister, B.E.; Glinchuk, M.D. Dipole glass and ferroelectricity in random-site electric-dipole systems. Rev. Mod. Phys. 1990, 62, 993–1026. [Google Scholar] [CrossRef]
- Mydosh, J.A. Spin Glasses; Taylor & Francis: London, UK, 1993; pp. 3–9. [Google Scholar]
- Snyder, J.; Slusky, J.S.; Cava, R.J.; Schiffer, P. How ‘spin ice’ freezes. Nature 2001, 413, 48–51. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Ren, X.B.; Otsuka, K. Shape memory effect and superelasticity in a strain glass alloy. Phys. Rev. Lett. 2006, 97, 225703. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Zhang, Z.; Zhang, J.A.; Zhou, Y.M.; Wang, Y.; Ding, X.D.; Wang, Y.Z.; Ren, X.B. Strain glass in Fe-doped Ti-Ni. Acta Mater. 2010, 58, 6206–6215. [Google Scholar] [CrossRef]
- Chien, C.; Tsao, C.S.; Wu, S.K.; Chang, C.Y.; Chang, P.C.; Kuo, Y.K. Characteristics of the strain glass transition in as-quenched and 250 °C early-aged Ti48.7Ni51.3 shape memory alloy. Acta Mater. 2016, 120, 159–167. [Google Scholar] [CrossRef]
- Ji, Y.C.; Ding, X.D.; Lookman, T.; Otsuka, K.; Ren, X.B. Heterogeneities and strain glass behavior: Role of nanoscale precipitates in low-temperature-aged Ti48.7Ni51.3 alloys. Phys. Rev. B 2013, 87, 104110. [Google Scholar] [CrossRef]
- Glatter, O.; Kratky, O. Small Angle X-ray Scattering; Academic Press: Cambridge, MA, USA, 1982; p. 222. [Google Scholar]
- Tsao, C.S.; Huang, E.W.; Wen, M.H.; Kuo, T.Y.; Jeng, S.L.; Jeng, U.S.; Sun, Y.S. Phase transformation and precipitation of an Al-Cu alloy during non-isothermal heating studied by in situ small-angle and wide-angle scattering. J. Alloys Compd. 2013, 579, 138–146. [Google Scholar] [CrossRef]
- Huang, E.W.; Tsao, C.S.; Wen, M.H.; Kuo, T.Y.; Tu, S.Y.; Wu, B.W.; Su, C.J.; Jeng, U.S. Resolution of structural transformation of intermediates in Al-Cu alloys during non-isothermal precipitation. J. Mater. Res. 2014, 29, 874–879. [Google Scholar] [CrossRef]
- Tsao, C.S.; Chen, C.Y.; Jeng, U.S.; Kuo, T.Y. Precipitation kinetics and transformation of metastable phases in Al-Mg-Si alloys. Acta Mater. 2006, 54, 4621–4631. [Google Scholar] [CrossRef]
- Dorin, T.; Deschamps, A.; De Geuser, F.; Lefebvre, W.; Sigli, C. Quantitative description of the T-1 formation kinetics in an Al-Cu-Li alloy using differential scanning calorimetry, small-angle X-ray scattering and transmission electron microscopy. Philos. Mag. 2014, 94, 1012–1030. [Google Scholar] [CrossRef]
- De Geuser, F.; Malard, B.; Deschamps, A. Microstructure mapping of a friction stir welded AA2050 Al-Li-Cu in the T8 state. Philos. Mag. 2014, 94, 1451–1462. [Google Scholar] [CrossRef] [Green Version]
- Deschamps, A.; Brechet, Y. Influence of predeformation and ageing of an Al-Zn-Mg alloy—II. Modeling of precipitation kinetics and yield stress. Acta Mater. 1998, 47, 293–305. [Google Scholar] [CrossRef]
- Deschamps, A.; Livet, F.; Brechet, Y. Influence of predeformation on ageing in an Al-Zn-Mg alloy—I. Microstructure evolution and mechanical properties. Acta Mater. 1998, 47, 281–292. [Google Scholar] [CrossRef]
- Nicolas, M.; Deschamps, A. Characterisation and modelling of precipitate evolution in an Al-Zn-Mg alloy during non-isothermal heat treatments. Acta Mater. 2003, 51, 6077–6094. [Google Scholar] [CrossRef]
- Dumont, M.; Lefebvre, W.; Doisneau-Cottignies, B.; Deschamps, A. Characterisation of the composition and volume fraction of η and η′ precipitates in an Al-Zn-Mg alloy by a combination of atom probe, small-angle X-ray scattering and transmission electron microscopy. Acta Mater. 2005, 53, 2881–2892. [Google Scholar] [CrossRef]
- Hutchinson, C.R.; de Geuser, F.; Chen, Y.; Deschamps, A. Quantitative measurements of dynamic precipitation during fatigue of an Al-Zn-Mg-(Cu) alloy using small-angle X-ray scattering. Acta Mater. 2014, 74, 96–109. [Google Scholar] [CrossRef]
- Tsao, C.S.; Lin, T.L.; Yu, M.S. δ′ precipitation in Al-9.7at%Li alloy using small-angle X-ray scattering. J. Alloys Compd. 1999, 289, 81–87. [Google Scholar] [CrossRef]
- Panagos, P.; Wang, Y.; McCartney, D.G.; Li, M.; Ghaffari, B.; Zindel, J.W.; Miao, J.; Makineni, S.; Allison, J.E.; Shebanova, O.; et al. Characterising precipitate evolution in multi-component cast aluminium alloys using small-angle X-ray scattering. J. Alloys Compd. 2017, 703, 344–353. [Google Scholar] [CrossRef]
- Prasher, M.; Sen, D. Influence of aging on phase transformation and microstructure of Ni50.3Ti29.7Hf20 high temperature shape memory alloy. J. Alloys Compd. 2014, 615, 469–474. [Google Scholar] [CrossRef]
- Xu, H.J.; Lu, Z.; Ukai, S.; Oono, N.; Liu, C.M. Effects of annealing temperature on nanoscale particles in oxide dispersion strengthened Fe-15Cr alloy powders with Ti and Zr additions. J. Alloys Compd. 2017, 693, 177–187. [Google Scholar] [CrossRef]
- Saida, J.; Yamada, R.; Kozikowski, P.; Imafuku, M.; Sato, S.; Ohnuma, M. Characterization of nano-quasicrystal-formation in correlation to the local structure in Zr-based metallic glasses containing Pd. J. Alloys Compd. 2017, 707, 46–50. [Google Scholar] [CrossRef]
- De Geuser, F.; Styles, M.J.; Hutchinson, C.R.; Deschamps, A. High-throughput in-situ characterization and modeling of precipitation kinetics in compositionally graded alloys. Acta Mater. 2015, 101, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Deschamps, A.; Garcia, M.; Chevy, J.; Davo, B.; De Geuser, F. Influence of Mg and Li content on the microstructure evolution of Al-Cu-Li alloys during long-term ageing. Acta Mater. 2017, 122, 32–46. [Google Scholar] [CrossRef]
- Gumbmann, E.; De Geuser, F.; Sigli, C.; Deschamps, A. Influence of Mg, Ag and Zn minor solute additions on the precipitation kinetics and strengthening of an Al-Cu-Li alloy. Acta Mater. 2017, 133, 172–185. [Google Scholar] [CrossRef]
- Biswas, A.; Sen, D.; Sarkar, S.K.; Sarita; Mazumder, S.; Seidman, D.N. Temporal evolution of coherent precipitates in an aluminum alloy W319: A correlative anisotropic small angle X-ray scattering, transmission electron microscopy and atom-probe tomography study. Acta Mater. 2016, 116, 219–230. [Google Scholar] [CrossRef]
- Kim, J.I.; Miyazaki, S. Comparison of shape memory characteristics of a Ti-50.9 At. Pct Ni alloy aged at 473 and 673 K. Metall. Mater. Trans. A 2005, 36, 3301–3310. [Google Scholar] [CrossRef]
- Kim, J.I.; Miyazaki, S. Effect of nano-scaled precipitates on shape memory behavior of Ti-50.9 at % Ni alloy. Acta Mater. 2005, 53, 4545–4554. [Google Scholar] [CrossRef]
- Fratzl, P.; Langmayr, F.; Paris, O. Evaluation of 3D small-angle scattering from nonspherical particles in single-crystals. J. Appl. Crystallogr. 1993, 26, 820–826. [Google Scholar] [CrossRef]
- De Geuser, F.; Bley, F.; Deschamps, A. A new method for evaluating the size of plate-like precipitates by small-angle scattering. J. Appl. Crystallogr. 2012, 45, 1208–1218. [Google Scholar] [CrossRef]
- Yen, F.-C.; Hwang, K.-S.; Wu, S.-K. Fabrication of porous Ti-rich Ti51Ni49 by evaporating NaCl space holder. Metall. Mater. Trans. A 2014, 45, 2626–2635. [Google Scholar] [CrossRef]
- Nishida, M.; Wayman, C.M.; Honma, T. Precipitation processes in near-equiatomic TiNi shape memory alloys. Metall. Trans. A 1986, 17, 1505–1515. [Google Scholar] [CrossRef]
- Arciniegas, M.; Casals, J.; Manero, J.M.; Peña, J.; Gil, F.J. Study of hardness and wear behaviour of NiTi shape memory alloys. J. Alloys Compd. 2008, 460, 213–219. [Google Scholar] [CrossRef]
- Chen, Q.; Wu, X.F.; Ko, T. The effects of Ti3Ni4 precipitates on the R-phase transformation. Scr. Metall. Mater. 1993, 29, 49–53. [Google Scholar] [CrossRef]
- Kline, S.R. Reduction and analysis of SANS and USANS data using IGOR Pro. J. Appl. Crystallogr. 2006, 39, 895–900. [Google Scholar] [CrossRef]
- Tsao, C.S.; Li, M.; Zhang, Y.; Leao, J.B.; Chiang, W.S.; Chung, T.Y.; Tzeng, Y.R.; Yu, M.S.; Chen, S.H. Probing the room temperature spatial distribution of hydrogen in nanoporous carbon by use of small-angle neutron scattering. J. Phys. Chem. C 2010, 114, 19895–19900. [Google Scholar] [CrossRef]
- Deschamps, A.; Brechet, Y.; Livet, F. Influence of copper addition on precipitation kinetics and hardening in Al-Zn-Mg alloy. Mater. Sci. Technol. 1999, 15, 993–1000. [Google Scholar] [CrossRef]
- Ren, X.B. Strain glass and ferroic glass—Unusual properties from glassy nano-domains. Phys. Status Solidi B 2014, 251, 1982–1992. [Google Scholar] [CrossRef]
- Fan, G.; Zhou, Y.; Chen, W.; Yang, S.; Ren, X.; Otsuka, K. Precipitation kinetics of Ti3Ni4 in polycrystalline Ni-rich TiNi alloys and its relation to abnormal multi-stage transformation behavior. Mater. Sci. Eng. A 2006, 438, 622–626. [Google Scholar] [CrossRef]
- Filip, P.; Mazanec, K. On precipitation kinetics in TiNi shape memory alloys. Scr. Mater. 2001, 45, 701–707. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of phase change I—General theory. J. Chem. Phys. 1939, 7, 1103–1112. [Google Scholar] [CrossRef]
- Johnson, W.A.; Mehl, R.F. Reaction kinetics in processes of nucleation and growth. Trans. Metall. AIME 1939, 135, 416–442. [Google Scholar]
- Kolmogoroff, A. Zur Statistik der Kristallisationsvorgänge in Metallen. Izv. Akad. Nauk SSSR Ser. Mater. 1937, 1, 355–359. [Google Scholar]
- Esmaeili, S.; Lloyd, D.J.; Poole, W.J. Modeling of precipitation hardening for the naturally aged Al-Mg-Si-Cu alloy AA6111. Acta Mater. 2003, 51, 3467–3481. [Google Scholar] [CrossRef]
- Dorin, T.; Deschamps, A.; De Geuser, F.; Sigli, C. Quantification and modelling of the microstructure/strength relationship by tailoring the morphological parameters of the T-1 phase in an Al-Cu-Li alloy. Acta Mater. 2014, 75, 134–146. [Google Scholar] [CrossRef]
- Deschamps, A.; Sigli, C.; Mourey, T.; de Geuser, F.; Lefebvre, W.; Davo, B. Experimental and modelling assessment of precipitation kinetics in an Al-Li-Mg alloy. Acta Mater. 2012, 60, 1917–1928. [Google Scholar] [CrossRef]








| Aging Time (h) | 0 | 1 | 3 | 5 | 10 | 20 |
|---|---|---|---|---|---|---|
| Tg,1Hz (°C) | −56.7 | −46.9 | −37.5 | −19.6 | −7.29 | 3.55 |
| ΔTg (°C) | 11.1 | 3.9 | 2.5 | 2.0 | 1.38 | 0.38 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.-C.; Tsao, C.-S.; Wu, S.-K. A Study on the Nanoparticles Evolution in Isothermally Aged Strain Glass of Ti48.7Ni51.3 Shape Memory Alloy by In Situ Small-Angle X-ray Scattering. Metals 2018, 8, 352. https://doi.org/10.3390/met8050352
Huang Y-C, Tsao C-S, Wu S-K. A Study on the Nanoparticles Evolution in Isothermally Aged Strain Glass of Ti48.7Ni51.3 Shape Memory Alloy by In Situ Small-Angle X-ray Scattering. Metals. 2018; 8(5):352. https://doi.org/10.3390/met8050352
Chicago/Turabian StyleHuang, Yung-Chien, Cheng-Si Tsao, and Shyi-Kaan Wu. 2018. "A Study on the Nanoparticles Evolution in Isothermally Aged Strain Glass of Ti48.7Ni51.3 Shape Memory Alloy by In Situ Small-Angle X-ray Scattering" Metals 8, no. 5: 352. https://doi.org/10.3390/met8050352
APA StyleHuang, Y. -C., Tsao, C. -S., & Wu, S. -K. (2018). A Study on the Nanoparticles Evolution in Isothermally Aged Strain Glass of Ti48.7Ni51.3 Shape Memory Alloy by In Situ Small-Angle X-ray Scattering. Metals, 8(5), 352. https://doi.org/10.3390/met8050352