Real-Time Investigation of Recovery, Recrystallization and Austenite Transformation during Annealing of a Cold-Rolled Steel Using High Energy X-ray Diffraction (HEXRD)

Abstract

The annealing process of cold-rolled ferrite/pearlite steel involves numerous metallurgical mechanisms as recovery/recrystallization of deformed phases, ripening of carbide microstructure, and austenite transformation in the intercritical domain. The interactions between these mechanisms govern the morphogenesis of the transformed austenite microstructure and, thus, the final properties of the steel. This paper demonstrates that high energy X-ray diffraction (HEXRD) on synchrotron beamline offers the unique possibility to follow concomitantly these mechanisms in situ during a single experiment. A cold-rolled ferrite-pearlite steel dedicated to the industrial production of Dual-Phase steel serves as case-study. Synchrotron experiments have been conducted in transmission at 100 keV with a 2D detector. Diffraction patterns acquired all along an annealing treatment are first analyzed after circular integration. A Rietveld refinement procedure coupled with a Williamson-Hall approach is used to determine phase transformation and recovery kinetics. In this paper, a new method inspired by the 3D X-ray diffraction tomography is proposed to follow recrystallization kinetics at the same time. It is based on a systematic detection of individual diffraction spots related to newly recrystallized grains appearing on Debye-Scherrer rings. The deduced recrystallization kinetics is compared and validated by more conventional ex situ methods.

1. Introduction

Dual-Phase (DP) Ferrite-Martensite steel presents a good formability, which permits the design of complex shapes for automotive structural elements [1]. Their heterogeneous microstructures are made of hard martensite islands dispersed in a ductile ferrite/bainite matrix [2,3]. Most of low thickness industrial DP steel sheets are produced through a continuous annealing process of cold-rolled ferrite-pearlite semi-products at high temperature in the ferrite/austenite intercritical domain. Consistently, the final microstructure is obtained after the last cooling of the annealing stage. The control of the austenite volume fraction at high temperature is, thus, essential to achieve targeted mechanical properties [3].

The austenite transformation kinetics from deformed ferrite-pearlite microstructures as well as the topology of the final microstructure depends strongly on the recrystallization state of the ferritic matrix. The possibility for using this interaction between recovery, recrystallization, and phase transformation is currently seen as a powerful metallurgical lever to improve the final performances of DP steels [1,4,5,6,7,8,9]. This paper aims to demonstrate that high energy X-ray diffraction (HEXRD) on synchrotron beamline offers the possibility to follow concomitantly these mechanisms in situ and during a single experiment. A cold-rolled ferrite-pearlite steel used for industrial dual-phase steel production will serve as a case study.

HEXRD (or synchrotron XRD) is, in fact, more and more used in metallurgy since it provides numerous advantages compared to experiments at lower energy as:

• Fast and easy determination of residual stresses. For instance, it has been used by Oliveira et al. [10] to determine the residual stresses field across the bulk heat affected zone of a laser weld with a superior spatial resolution. In transmission or in reflection, it enables measurements on films [11,12], which are not imaginable with laboratory diffractometers.
• Time-resolved measurements of lattice parameters in phases during mechanical testing without unloading. As a consequence, the load-partitioning between phases during mechanical testing can be studied in bulk and in situ [13,14].
• In situ studies of solid-solid phase transformations mechanisms under thermomechanical treatments. The 2D diffraction patterns serve to track the respective evolution of phase fractions but also their lattice parameters, which depend on their local compositions and internal stresses (Please refer, for instance, to References [15,16,17,18,19,20] for in situ thermal treatments or to References [13,21] for strain induced transformation during in situ tensile tests). It has been proven that the HEXRD experiment is the sole reliable method to measure carbon enrichment in austenite in real time during a Quenching and Partitioning treatment of steel thanks to a high acquisition rate (10Hz) and it allows the unambiguous deconvolution of the chemical and mechanical contribution in austenite lattice parameters’ evolution [17].
• In situ estimates of the density and the arrangements of defects. Sallez et al. have, for instance, studied the recovery and nano-crystallization of oxide dispersion-strengthened ferritic steel [22]. The density of dislocations and the nano-crystallite sizes were determined using modified Williamson-Hall and Warren–Averbach methods [23]. More advanced post-treatment methods can be used as extended convolutional multiple-whole-profile (eCMWP) [24,25,26], as shown by Li et al. [27].

Based on the knowledge of the author, HEXRD have never been used to determine bulk recrystallization kinetics of micrometric conventional steels. However, Jensen at al. [28,29,30] have recently shown that recrystallization kinetics of individual grains in deformed aluminum or copper can be followed in real-time using 3D-XRD tomography. In the proposed experiments, each individual diffraction spots emerging from Debye-Scherrer (DS) rings is followed assuming that it corresponds to a newly recrystallized grain. Since the intensities of the spots are supposed to be proportional to the volumes of the studied new grains, growth kinetics of individual grains as well as precise nucleation conditions can be determined from few in situ experiments. At the same time, the position and local crystallographic orientations of new grains can be tracked in bulk. Mean recrystallization kinetics can be deduced but without guarantee of its statistical representativeness on larger volumes (low number of considered grains). Moreover, since 3D-XRD cannot be applied reasonably to grains smaller than 5 µm, the case of industrial steel discussed above cannot be treated.

Inspired by these prior works on 3DXRD, the present article proposes a new in situ method based on HEXRD experiments to determine mean recrystallization kinetics in bulk, considering a large number of grains. It will be illustrated with a study on ferrite-pearlite steel but remains general and applicable to other polycrystalline metals. In the studied case, it will be shown that, in situ HEXRD permits the study of simultaneously recovery, recrystallization, and phase transformation during the annealing schedule.

2. Materials and Methods

2.1. As-Received Material

The investigated material is dedicated to the production of industrial cold-rolled and annealed dual-phase steel and its composition is Fe-0.1C-1.9Mn-0.2Cr-0.2Si (wt.%). Cuboid samples 10 × 5 × 1.2 mm³ have been machined from industrial steel sheets at manufacturing states prior to continuous annealing (as-hot rolled and as-cold rolled). The samples in the cold-rolled state have been used for both in situ and ex situ annealing experiments described below.

The initial microstructure in the as-hot rolled state before cold-rolling, i.e., after rolling at high temperature and coiling, is made of polygonal ferrite and lamellar pearlite. The volume fraction of latter pearlite is about 16%. The microstructure contains a number of intergranular cementite carbides dispersed in the ferritic matrix. The cold-rolling ratio then applied to the studied steel is 60%, which corresponds to a severe plastic equivalent deformation of 106% in bulk. During such a process, since pearlite shows a higher flow stress than ferrite, the local deformation is even higher in the ferritic matrix. In order to estimate this strain partitioning, the model proposed by Bouaziz et al. [31] further improved by Allain et al. [32] has been used. This micromechanical approach takes into the behavior law of both phases and estimate the strain and load partitioning by scale transition using an iso-work assumption. For the studied rolling conditions (plastic equivalent deformation of 106%), the model predicts a deformation of 119% in ferrite and 67% in pearlite accounting for their respective fraction. The same physically-based model provides an estimation of the density of dislocations. For the studied case, this density is estimated around 4 × 10¹⁵ m⁻² in ferrite after cold-rolling. The Figure 1 shows two SEM micrographs of the steel before and after cold-rolling (picral etching), respectively.

2.2. Microsctructure Observations

Microstructure characterizations have been carried out using two SEMs. Micrographs in Secondary Electron (SE) mode have been obtained on a XL30 FEG-SEM (Philipps, Amsterdam, The Netherland) microscope after polishing and 2% picral or metabisulfite etching and ESBD maps have been obtained on a Jeol JSM-7001F FEG-SEM (Jeol, Tokyo, Japan) coupled with a Channel 5 HKL (Oxford Instrument, Abingdon, UK) set-up. These observations have been made ex situ on samples prior to annealing (cf. Figure 1) or after interrupted annealing treatments.

As shown by Radwański [33], a grain orientation spread representation (GOS) [34,35] extracted from the EBSD map permits characterizing the recrystallization states of the steel. Our EBSD maps have, thus, been post-treated to reveal the residual deformation in grains (geometrically necessary dislocations). Boundaries of deformed and recrystallized grains have first been detected. The threshold value of the pixel-to-pixel misorientation to define a grain boundary has been set to 5°. The grain orientation spread is then calculated as the standard deviation of crystallographic misorientation inside the studied grain as its mean orientation. Thus, the higher the GOS value, the more the grain is deformed. Radwański considered that a grain is non-recrystallized if its GOS value is higher than 1.5°. This threshold value has also been considered to estimate the mean un-recrystallized volume fraction in this work.

2.3. Diffraction Set-Ups and Furnace Used for the In Situ Experiment

The HEXRD experiment was carried out at the Deutsches Electronen-SYnchrotron on the PETRA III P07 beamline (DESY, Hamburg, Germany). It has been operated with a powder diffraction set-up in transmission. The size of the high energy monochromatic beam (energy 100 keV, wavelength 0.012398 nm) is 400 × 400 µm² broad, which means that approximatively 50,000 grains were scanned through the thickness of the sample. Calibration has been performed using Fit2D software (v18, ESRF, Grenoble, France) [36,37] to adjust the sample to detector distance and correct the detector tilts using LaB6 powder. The distance was set to 1.251 m. The diffraction patterns were recorded at a high rate (10 Hz) on a PerkinElmer 2-D (PerkinElmer, Waltham, MA, USA) plate detector, producing more than 2700 images for the discussed experiment (in about 4 min). The set-up is similar to the one used by Reference [17]. The thermal cycle was performed in a modified Bähr 805 A/D (TAinstruments, New Castle, DE, USA) dilatometer. During the considered in situ experiment, the sample is heated to a peak temperature of 800 °C at a constant heating rate (3 °C·s⁻¹) to mimic an industrial schedule [2].

2.4. Processing of Synchrotron Diffraction Experiments

2.4.1. Phase Transformation Kinetics

A Rietveld analysis [38] was conducted to determine the phase transformation kinetics and the evolution of the dislocation density. Pictures of Debye-Scherrer (DS) rings have been integrated using the Fit2D software. The 1D diffraction pattern was then refined with Fullprof software (V2.05, ILL, Grenoble, France) in a 2θ range from 2.70° to 8.70° using Pseudo-Voigt functions [39]. Only two phases have been considered (ferrite and austenite) as peaks due to cementite that can be observed. The two phases are difficult to de-convolute from the background signal. The minimum detectable austenite mass fraction is about 2% with such a procedure. This value corresponds to the accuracy of the phase fraction measurement [17].

2.4.2. Recovery Kinetics

From the shape of diffraction peaks, it has been possible to estimate the evolution of dislocation density in ferrite using the Williamson-Hall method [23]. Equation (1) permits a correlation to the Full Width Half Maximum (FWHM) of diffraction peaks for a given diffraction angle θ to the parameter ε representing the mean deformation of the material and to a crystallite size D [40]. In our refinement procedure, the FWHM of the diffraction peaks of ferrite have been modeled using Caglioti’s coefficients [38,39]. Hence, considering the FWHM of (110), (200), (211), (220), and (310) ferrite peaks, it has been possible using a linear regression to estimate the evolution of ε and D all along the thermal treatment. The equation relating the FWHM to ε and D is given below.

$$\mathrm{FWHM}\left(\mathsf{\theta }\right)·\cos \mathsf{\theta }=\frac{\mathrm{K}·\mathsf{\lambda }}{\mathrm{D}}+4\sin \mathsf{\theta }·\mathsf{\epsilon }$$

(1)

K is a constant, set to 0.9, and λ is the wavelength of the incident beam. The reader is referred to Reference [23] for more details. In the procedure explained above, the experimental peak broadening has been measured using LaB₆ diffraction patterns and subtracted from the experimental patterns [40]. This procedure has been applied to all recorded patterns up to Ac1 when the austenite transformation starts since diffraction peaks of ferrite and austenite overlap above this temperature. This overlapping leads to a decrease in the confidence index of the refinement procedure.

The dislocation density ρ (m⁻²) was calculated knowing ε and D thanks to Smallman’s formula [41].

$$\mathsf{\rho }=\frac{3\sqrt{2\mathsf{\pi }}\mathsf{\epsilon }}{\mathrm{bD}}$$

(2)

where b is the Burger vector of perfect dislocations in ferrite (b = 2.58 × 10⁻¹⁰ m [3]).

2.4.3. Recrystallization Kinetics—A New Methodology

The detailed observation of DS rings has revealed the appearance of individual diffraction spots all along the rings during the studied annealing sequence temperature above 650 °C. Figure 2a–c show, for instance, the 2D diffraction pattern images captured at 25 °C and 700 °C (full scale and magnified views). In Figure 2c, the image contrast has been improved to distinguish the individual spots despite the high intensity of the DS rings. These spots are presumably due to the new recrystallized grains and their kinetics of apparition should be related to the recrystallization kinetics. Jensen et al. [28,29,30] have shown that it is possible to use these individual diffraction spots to compare the recrystallization processes for different initial grain orientations. Savran et al. [42] has proposed an experiment based on a similar idea to measure the nucleation rate of austenite in low carbon steel. Nevertheless, from our best knowledge, these individual spots have never been exploited to quantify bulk recrystallization kinetics while the density of spots is presumably correlated to the density of new recrystallized grains. It, however, supposes that the gradient of misorientations inside the new recrystallized grains is weak to observe concentrated spots and to be able to deconvolute these spots from the continuous diffraction rings of the studied phase. Therefore, following the inspiring works of Jensen et al., we have developed an original method to estimate bulk recrystallization kinetics.

In practice, our method first consists of integrating radially the DS rings at each azimuthal position since it is more convenient to work in 1D than trying to detect individual spots in 2D images close to intense DS rings. In the studied case, the (200) ring has been investigated in detail as it permits to avoid possible overlap with austenite above Ac1. The integration has been made using Fit2D software in between an inner and an outer circular bound to produce a closed area embedding the whole studied DS ring. The width between inner and circular bounds corresponds to about four times the FWHM of the considered ring. The latter area is then divided into angular sectors. The number of sectors actually determines the angular resolution of the azimuthal integration. The binning rate has been set to 2575 bins in Fit2D software for the treatment of (200) ring. This value has been chosen according to the resolution of the detector (2048 × 2048 pixels) to a coincidence between 1 bin and 1 pixel along the studied ring, i.e., guaranteeing the highest possible resolution. The ring is integrated in the angular range 0–360° with 0° corresponding to the horizontal axis of 2D diffractograms. Figure 2d represents the integrated intensity of the (200) DS at room temperature (black) and at 700 °C (red), respectively. The profile at room temperature shows four periodic main peaks due to the cold-rolling texture. In the following, these main variations of intensity with an azimuthal angle will be called “texture peaks.” Apart from texture peaks, the profile is relatively smooth with limited statistical fluctuations. On the contrary, the profile at 700 °C still shows the four texture peaks but also numerous small fluctuations. The highest fluctuations are found in the vicinity of the 90° and 270° positions. These fluctuations are due to the individual diffraction spots observed in DS rings. In the following, those individual intensity fluctuations will be designated as “recrystallization peaks.”

After azimuthal integration, the number of recrystallization peaks on the considered ring is counted on each 1D diffractogram similar to Figure 2d. To this end, a specific algorithm was developed to identify each recrystallization peak from a mean textured diffraction signal. The procedure is based on local rules without interpolation functions permitting to detect possible recrystallization peaks independently on texture peaks. The algorithm first detects all fluctuations on 1D azimuthal intensity profiles by searching points with lower intensity values on its left and right sides (finally an upward segment followed by a downward segment along the profile) and measure the total height of the detected fluctuation (difference between the maximum intensity value and the lowest value detected on its sides). Fluctuations are then numbered and the statistical distribution of their heights is calculated. A threshold value has also been considered in the algorithm to avoid counting statistical fluctuations of the signal (background noise). This value has been set in order to avoid 90% of statistical fluctuations recorded at room temperature, i.e., in the absence of recrystallization peaks. In such a manner, the purely statistical fluctuations are excluded from recrystallization peaks counting. As a consequence, the method is sensitive to the angular resolution chosen for azimuthal integration. It is, thus, impossible to interpret the absolute number of detected peaks because one recrystallization peak does not necessarily correspond to one new single grain. However, the relative evolution of the recrystallization peak number is believed to be representative of the bulk recrystallization kinetics.

Since the sample is not rotated during the experiment, it is impossible to get diffraction signals from all newly recrystallized grains and, thus, new grains from certain texture fibers will never be in diffraction conditions. To reduce the associated bias, we have conducted our analysis systematically on different rings. In the studied steel, it happens that the deduced evolutions of recrystallization peak densities from these rings are similar. DP steels are, in fact, known to show very limited recrystallization textures contrary to fully ferritic steels or aluminum alloys [2]. As a consequence, this source of uncertainty has been neglected in the present paper but this question is certainly worth investigating and this bias was quantified in the future with more complex diffraction set-ups.

3. Results

According to the literature, the annealing process of cold-rolled ferrite/pearlite steel involves numerous metallurgical mechanisms as recovery/recrystallization of deformed ferrite and pearlite, ripening of carbides below Ac1 temperature (lower limit of the intercritical domain), and the austenite transformation above Ac1. Below Ac1, the recovery processes consist in the reorganization of the dislocation structures and in a decrease in the dislocation density in the deformed grains, which leads to a decrease in the stored strain energy. This phenomenon occurs at a relatively low temperature and is followed by the recrystallization of the ferrite grains (new “defect free” grains) if the remaining stored energy is sufficient. The complexity arises as the recrystallization kinetics is reduced within pearlite structures. The recovery/recrystallization are, thus, highly coupled phenomena in these alloys and the coupling depends on the heating rates and the evolutions of pearlite islands (ripening and coalescence).

In this section, we will show how the diffraction patterns obtained during the in situ experiment have been analyzed by different independent methods to extract the kinetics of austenite transformation, the recovery, and the recrystallization of the ferrite matrix, respectively. This combination enables the time-resolved study of the interactions of these three mechanisms.

3.1. Phase Transformation Kinetics

The evolution of the austenite phase fraction during applied thermal treatment is represented in Figure 3a. It appears that transformation starts at 710 °C (Ac1 = 710 °C) and the austenite phase fraction reaches about 47% at 800 °C. The austenite formation kinetics is relatively slow at the beginning of the transformation up to a temperature of 745 °C. Afterward, the transformation proceeds significantly faster up to the peak temperature due to pearlite fast dissolution presumably.

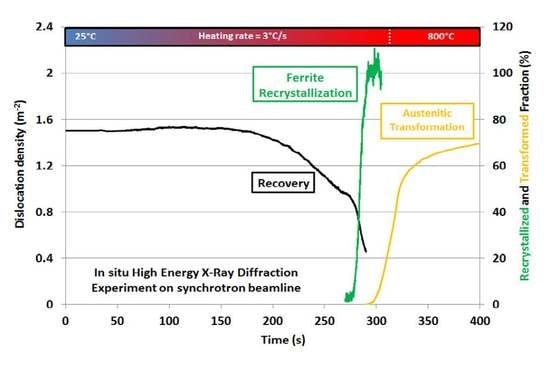
3.2. Recovery Kinetics

The evolution of the density of dislocations deduced from our systematic Williamson-Hall analysis during heating has been plotted in Figure 3b. Even if the accuracy and the validity of Equation (2) can be discussed, it enables highlighting the major evolutions in the studied material. In the studied steel, the initial density ρ₀ before heating is estimated at about 1.5 × 10¹⁵ m⁻², which is consistent with values found by our micromechanical model (see Section 2.1) and valued found in the literature [43] for cold-rolled steel. The evolution of the dislocation density as a function of time is represented in Figure 3b. During heating, it follows three well distinctive stages.

• Stage 1: No evolution—constant density for temperatures lower than 380 °C.
• Stage 2: Decrease in ρ₀ by one-third between 380 °C and 650 °C.
• Stage 3: Sharp decrease up to Ac1 (710 °C). ρ₀ is reduced again by one-third.

Stage 2 corresponds to the temperature range where recovery is expected to occur [2]. Consistently, stage 3 might correspond to the recrystallization process. The Williamson-Hall method, thus, enables detecting the start/end temperatures for recovery of the ferrite matrix with a good precision and provides as reasonable an estimate of the decrease in dislocation density. It seems also possible from this analysis to infer a possible start temperature for recrystallization. This conjunction has also been reported by Reference [27].

3.3. Recrystallization Kinetics

Figure 4a shows the evolution of the counted recrystallization peaks as a function of the temperature (black dots) on recorded (200) DS rings. The evolution of the dislocation density (blue curve) is overlaid for the sake of comparison. With the procedure described above, the number of detected peaks remains close to zero up to 670 °C and suddenly increases to a maximum value of approximatively 250 peaks at 720 °C. The increase shows a sigmoidal shape with a saturation plateau after 720 °C. Above 740 °C, the number of detected peaks decreases again. The weak scattering of the experimental values around the mean evolution clearly sustains our approach. The same work has been conducted on others rings with similar conclusions (same relative trends but not same absolute numbers of peaks).

As expected, stage 3 of the recovery starts when first significant recrystallization peaks appear on diffraction rings. The concomitance between both events is noteworthy and, thus, provides a convincing and precise measure of the recrystallization start temperature for the studied steel in the studied heating conditions (670 °C at 3 °C·s⁻¹).

The evolution of the number of new individual spots on diffraction rings can only be strictly related to the nucleation process on new recrystallized grains, as shown by Savran et al. [42] when studying the first stage of austenite phase transformation. This is also implicitly the hypothesis made by Jensen et al. [28,29,30]. However, if one considers as a first estimate that the growth of new recrystallized grains is limited and, thus, that recrystallization kinetics is dominated by nucleation [44], the relative evolution of new recrystallization peaks is directly correlated to the recrystallized fraction of the studied phase. The assumption that the growth of recrystallized grains in the studied case is limited is confirmed by our complimentary SEM/EBSD observations presented in the next subsection as well by the fact that the shapes of individual spots do not evolve on successive 2D diffraction patterns during heating, which reveals the absence of lattice curvatures in new grains. Since a recrystallization peak cannot be unequivocally attributed to a single grain because of our counting procedure, it is not possible to keep track of the intensity of a single grain.

The number of counted peaks has, thus, been divided by the value found on the plateau between 720 °C and 740 °C (fully recrystallized ferrite state after our SEM observations) to provide a normalized density representative of the bulk recrystallization progress. The evolution deduced from HEXRD measurements is represented in Figure 4b. The deduced function shows a sigmoidal shape as expected from recrystallization kinetics.

Above 740 °C, Figure 4a shows that the number of recrystallization peaks on DS rings decreases. This decrease is due to the phase transformation process (more than 5% of austenite) since austenite phase transformation induces broadening of individual diffraction spots which, in turn, becomes less detectable as recrystallization peaks. Consequently, the number of diffraction peaks cannot be interpreted as straightforwardly as below Ac1.

The austenite transformation starts at nearly 10 °C before the full completion of recrystallization, which means that the interaction between recrystallization and phase transformation is negligible in the studied steel. This result is in good agreement with numerous previous reports on similar steels under similar heating conditions [1,4,5,6,7,8,9].

3.4. Validation by Microstructure Observations

To validate our recrystallization kinetics, the microstructures have been characterized after interrupted heating sequences. The samples were heated in a similar dilatometer at 3 °C·s⁻¹ up to a chosen temperature and then quenched. Figure 5a,b shows the SEM micrographs after etching of samples heated at 700 °C and 800 °C and Figure 5a,b shows the EBSD maps obtained on samples heated at 700 °C and 710 °C, respectively. At 700 °C, the microstructure is partially recrystallized. In Figure 5a, Picral etching reveals boundaries and sub-grains. Non-recrystallized domains contain numerous sub-grains whereas new recrystallized grains have a uniform contrast. In Figure 5c, the ESBD map has been post-treated to represent the Grain Orientation Spread (GOS). As shown by Reference [33], non-recrystallized domains (in green and in red, GOS value higher than 1.5°) present a higher spread than recrystallized grains (in blue, GOS value lower than 1.5°). The recrystallized volume fraction is about 73%. At 710 °C, the same method shown in Figure 5d gives a recrystallized fraction of 87%. The agreement is excellent with the value produced by our in situ method. Lastly, Figure 5b shows the microstructure after phase transformation after metabisulfite etching to reveal martensite from the ferritic matrix. At 800 °C, the ferrite microstructure is clearly fully recrystallized and the volume fraction of martensite is 45%, which is in agreement with our Rietvield analysis. These direct microstructure observations all sustain our new development.

4. Conclusions

In summary, it has been shown that it is possible to study simultaneously the recovery, the recrystallization, and the austenite phase transformation when heating a cold-rolled ferrite pearlite steel using in situ HEXRD experiments. Time-resolved investigations of recovery and phase transformation processes can be conducted by Rietveld analysis combined with the Williamson-Hall theory. For the studied steels, when heated up at 3 °C·s⁻¹, it has been shown that the recovering process starts at 380 °C and the Ac1 temperature is 710 °C. An original method based on the observation of the individual diffraction spots on 2D patterns has been developed to measure the recrystallization kinetics of the studied steel. In fact, new recrystallized grains produce intense diffraction spots that arise from the DS rings. The evolution of the number of individual spots is correlated to the nucleation of new grains and, thus, to the recrystallized fraction as far as the growth process is limited. We have shown in the studied case an excellent agreement between the recrystallized fraction measured by in situ HEXRD and a more conventional technique (GOS calculated by EBSD). The limits and the resolution of the method still needs to be studied but it offers a fantastic opportunity to study in real-time coupled phenomena in steel and other alloys.