Hot Deformation Behavior of a 2024 Aluminum Alloy Sheet and its Modeling by Fields-Backofen Model Considering Strain Rate Evolution
Abstract
:1. Introduction
2. Materials and Methods
3. Results
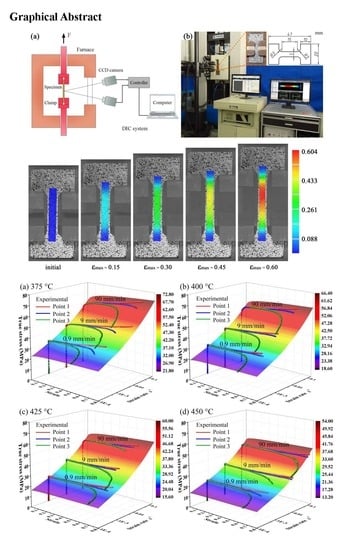
3.1. Non-uniform Flow Behavior
3.1.1. Strain Distribution
3.1.2. Local Stress-Strain Curves
3.1.3. Strain Rate Evolution
3.2. Improved Fields-Backofen Constitutive Model
3.2.1. Improved FB Model with Varied Strain Rates and its Determination
3.2.2. Verification of the Improved FB Models
4. Conclusions
- (1)
- The strain distribution during hot tensile tests was non-uniform on the reduced section of the sample. Concentrated strain distribution was observed when the maximum strain on the specimen was greater than 0.3. The percentage of uniform deformation area decreased linearly as the strain increased.
- (2)
- The local flow stress curves determined by different local points exhibited hardening, steady, and softening behaviors, respectively, resulting from the different strain rate evolutions during the tensile tests. The flow stress exhibited a hardening behavior when the strain rate increased with the proceeding of straining. It kept steady when the strain rate changed slightly. Obvious softening behavior was observed when the strain rate decreased with the increase of strain.
- (3)
- The improved FB constitutive model considering strain rate evolutions of local points showed a good agreement with experimental results. The hardening and softening behavior of the flow stress can be well predicted when varied strain rates of local points were considered in the equation. The improved FB model can describe the deformation behavior for continuously varied strain rate, resulting in an extended application of the model.
Author Contributions
Funding
Conflicts of Interest
References
- Hirsch, J. Recent development in aluminium for automotive applications. T. Nonferr. Metal. Soc. 2014, 24, 1995–2002. [Google Scholar] [CrossRef]
- Bressan, J.D.; Bruschi, S.; Ghiotti, A. Prediction of limit strains in hot forming of aluminium alloy sheets. Int. J. Mech. Sci. 2016, 115, 702–710. [Google Scholar] [CrossRef]
- Abedrabbo, N.; Pourboghrat, F.; Carsley, J. Forming of aluminum alloys at elevated temperatures—Part 1: Material characterization. Int. J. Plast. 2006, 22, 314–341. [Google Scholar] [CrossRef]
- Barnes, A.J. Superplastic Forming 40Years and Still Growing. J. Mater. Eng. Perform. 2007, 16, 440–454. [Google Scholar] [CrossRef]
- Krajewski, P.E.; Schroth, J.G. Overview of Quick Plastic Forming Technology. Mater. Sci. Forum 2007, 551, 3–12. [Google Scholar] [CrossRef]
- Fan, X.; He, Z.; Zheng, K.; Yuan, S. Strengthening behavior of Al–Cu–Mg alloy sheet in hot forming–quenching integrated process with cold–hot dies. Mater. Des. 2015, 83, 557–565. [Google Scholar] [CrossRef]
- El Fakir, O.; Wang, L.; Balint, D.; Dear, J.P.; Lin, J.; Dean, T.A. Numerical study of the solution heat treatment, forming, and in-die quenching (HFQ) process on AA5754. Int. J. Mach. Tools Manuf. 2014, 87, 39–48. [Google Scholar] [CrossRef] [Green Version]
- Shao, Z.; Li, N.; Lin, J.; Dean, T. Formability evaluation for sheet metals under hot stamping conditions by a novel biaxial testing system and a new materials model. Int. J. Mech. Sci. 2017, 120, 149–158. [Google Scholar] [CrossRef] [Green Version]
- Xiao, Z.B.; Huang, Y.C.; Liu, H.; Wang, S.X. Hot Tensile and Fracture Behavior of 35CrMo Steel at Elevated Temperature and Strain Rate. Metals 2016, 6, 210. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, X.M. A critical review of experimental results and constitutive descriptions for metals and alloys in hot working. Mater. Des. 2011, 32, 1733–1759. [Google Scholar] [CrossRef]
- Wang, S.X.; Huang, Y.C.; Xiao, Z.B.; Liu, Y.; Liu, H. A Modified Johnson-Cook Model for Hot Deformation Behavior of 35CrMo Steel. Metals 2017, 7, 337. [Google Scholar] [CrossRef]
- Chen, L.; Zhao, G.; Yu, J. Hot deformation behavior and constitutive modeling of homogenized 6026 aluminum alloy. Mater. Des. 2015, 74, 25–35. [Google Scholar] [CrossRef]
- Sun, Y.; Ye, W.H.; Hu, L.X. Constitutive Modeling of High-Temperature Flow Behavior of Al-0.62Mg-0.73Si Aluminum Alloy. J. Mater. Eng. Perform. 2016, 25, 1621–1630. [Google Scholar] [CrossRef]
- Jia, W.; Xu, S.; Le, Q.; Fu, L.; Ma, L.; Tang, Y. Modified Fields–Backofen model for constitutive behavior of as-cast AZ31B magnesium alloy during hot deformation. Mater. Des. 2016, 106, 120–132. [Google Scholar] [CrossRef]
- Chen, W.; Guan, Y.; Wang, Z. Modeling of Flow Stress of High Titanium Content 6061 Aluminum Alloy Under Hot Compression. J. Mater. Eng. Perform. 2016, 25, 4081–4088. [Google Scholar] [CrossRef]
- Zhang, X.H. Experimental and Numerical Study of Magnesium Alloy during Hotworking Process. Ph.D. Thesis, Shanghai Jiaotong University, Shanghai, China, 1 June 2003. [Google Scholar]
- Lin, Y.; Zhang, K.; He, Z.; Fan, X.; Yan, Y.; Yuan, S. Constitutive Modeling of the High-Temperature Flow Behavior of α-Ti Alloy Tube. J. Mater. Eng. Perform. 2018, 27, 2475–2483. [Google Scholar] [CrossRef]
- Hu, W.; Lin, Y.; Yuan, S.; He, Z. Constitutive models for regression of various experimental stress–strain relations. Int. J. Mech. Sci. 2015, 101, 1–9. [Google Scholar] [CrossRef]
- Belhabib, S.; Haddadi, H.; Gaspérini, M.; Vacher, P. Heterogeneous tensile test on elastoplastic metallic sheets: Comparison between FEM simulations and full-field strain measurements. Int. J. Mech. Sci. 2008, 50, 14–21. [Google Scholar] [CrossRef]
- Liu, W.; Guines, D.; Leotoing, L.; Ragneau, E. Identification of sheet metal hardening for large strains with an in-plane biaxial tensile test and a dedicated cross specimen. Int. J. Mech. Sci. 2015, 101, 387–398. [Google Scholar] [CrossRef]
- Kang, J.; Wilkinson, D.S.; Mishra, R.K.; Yuan, W.; Mishra, R.S. Effect of inhomogeneous deformation on anisotropy of AZ31 magnesium sheet. Mater. Sci. Eng. A 2013, 567, 101–109. [Google Scholar] [CrossRef]
- Yoon, J.I.; Kim, J.G.; Jung, J.M.; Lee, D.J.; Jeong, H.J.; Shahbaz, M.; Lee, S.; Kim, H.S. Obtaining reliable true plastic stress-strain curves in a wide range of strains using digital image correlation in tensile testing. Korean J. Metals Mater. 2016, 54, 231–236. [Google Scholar]
- Agirre, J.; Galdos, L.; Saenz de Argandoña, E.; Mendiguren, J. Hardening prediction of diverse materials using the Digital Image Correlation technique. Mech. Mater. 2018, 124, 71–79. [Google Scholar] [CrossRef]
- Abspoel, M.; Neelis, B.M.; van Liempt, P. Constitutive behaviour under hot stamping conditions. J. Mater. Process. Technol. 2016, 228, 34–42. [Google Scholar] [CrossRef]
- Wang, Z.B.; He, Z.B.; Fan, X.B.; Zhou, L.; Lin, Y.L.; Yuan, S.J. High temperature deformation behavior of friction stir welded 2024-T4 aluminum alloy sheets. J. Mater. Process. Technol. 2017, 247, 184–191. [Google Scholar] [CrossRef]
- Merklein, M.; Lechler, J. Investigation of the thermo-mechanical properties of hot stamping steels. J. Mater. Process. Technol. 2006, 177, 452–455. [Google Scholar] [CrossRef]
- Bariani, P.F.; Bruschi, S.; Ghiotti, A.; Michieletto, F. Deformation of AA6016 Aluminum Alloy Sheets at High Temperature and Strain Rate. Mater. Sci. Forum 2014, 783–786, 114–119. [Google Scholar] [CrossRef]










| Cu | Mg | Mn | Fe | Si | Zn | Ti | Ni | Al |
|---|---|---|---|---|---|---|---|---|
| 4.78 | 1.56 | 0.57 | 0.24 | 0.11 | 0.2 | 0.1 | 0.1 | Bal |
| Temperature (°C) | K | n | m |
|---|---|---|---|
| 375 °C | 93.789 | 0.0346 | 0.139 |
| 400 °C | 89.502 | 0.0305 | 0.153 |
| 425 °C | 81.618 | 0.0228 | 0.164 |
| 450 °C | 74.961 | 0.0144 | 0.180 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Z.; Wang, Z.; Lin, Y.; Fan, X. Hot Deformation Behavior of a 2024 Aluminum Alloy Sheet and its Modeling by Fields-Backofen Model Considering Strain Rate Evolution. Metals 2019, 9, 243. https://doi.org/10.3390/met9020243
He Z, Wang Z, Lin Y, Fan X. Hot Deformation Behavior of a 2024 Aluminum Alloy Sheet and its Modeling by Fields-Backofen Model Considering Strain Rate Evolution. Metals. 2019; 9(2):243. https://doi.org/10.3390/met9020243
Chicago/Turabian StyleHe, Zhubin, Zhibiao Wang, Yanli Lin, and Xiaobo Fan. 2019. "Hot Deformation Behavior of a 2024 Aluminum Alloy Sheet and its Modeling by Fields-Backofen Model Considering Strain Rate Evolution" Metals 9, no. 2: 243. https://doi.org/10.3390/met9020243
APA StyleHe, Z., Wang, Z., Lin, Y., & Fan, X. (2019). Hot Deformation Behavior of a 2024 Aluminum Alloy Sheet and its Modeling by Fields-Backofen Model Considering Strain Rate Evolution. Metals, 9(2), 243. https://doi.org/10.3390/met9020243