3. Experimental Technique
General information on SANS can be found in References [
15,
16]. For studying ferritic/martensitic steels, an external magnetic field of at least 1 T is needed to saturate the magnetization in the sample and separate the nuclear and the magnetic SANS cross-sections, as shown in
Figure 2. The total SANS cross-section is defined as follows:
where
2θ is the full scattering angle, λ the neutron wavelength,
Q = 4πsinθ/λ the modulus of the scattering vector, α the azimutal angle on the detector plane and Ω stands for the solid angle. The ratio of the SANS components measured in the directions perpendicular and parallel to the magnetic field, defined as follows:
is related to the nuclear and magnetic square differences in neutron scattering length density between the defects and the matrix,
and
, respectively [
15,
16].
It can provide information useful to identify the scattering defects: namely, for non-magnetic defects embedded in a fully magnetized matrix, it is equal to 2, while its dependence on
Q can imply the presence of different kinds of defects. In Eurofer97, assuming for the carbides a composition Cr
14Fe
8W
0.7V
0.3C
6 [
17] a nuclear contrast value of 2.13 × 10
20 cm
−4 is found for such precipitates; for micro-voids, the contrast is equal to the scattering length density of Eurofer97-1 itself, that is 5.51 × 10
21 cm
−4, while for helium bubbles it is 4.88 × 10
21 cm
−4 [
16]. Therefore, for comparable values of the corresponding volume fractions, both helium bubbles and micro-voids are expected to give rise to SANS effects one order of magnitude larger than precipitates, however, they are quite difficult to be distinguished from one another. A summary of the SANS set-up and experimental conditions selected to obtain the results analyzed in this paper is included in the next section.
The distributions of the scattering defects are obtained by inverse transformation of the experimental data. Namely, if their volume fraction is low and there is no inter-particle interference, the SANS nuclear and magnetic cross-sections can each be written as:
where
N(
R) is the number per unit volume of defects with a size between
R and
R + d
R,
V their volume,
their form factor and
is the nuclear or magnetic “contrast”.
The volume distribution function
D(R), average defect radius,
<R>, and volume fraction,
f, are defined respectively as follows:
where
Vtot is the total volume of the investigated sample.
N(
R) was determined by the method described in Reference [
18] and successfully utilized for several studies on technical steels, particularly those in References [
19,
20,
21]. This fitting procedure assumes no a priori shape of the defect distribution, representing it by a set of cubic B-spline functions, with knots uniformly distributed in a log
R scale and with the constraint
N(
R) > 0. The number of splines is chosen taking into account the
R-range
Rmin –
Rmax where the size distribution has to be investigated and the shape of the experimentally determined SANS cross-section. Knots spacing,
R-range, and a constant or
Q-dependent background are additional parameters, adjustable for improving the fit. The best-fit distribution is determined within an 80% confidence band. In general, the main difficulties in obtaining the distributions from Equation (3) arise from the fact that the SANS cross-section is measured only on a finite
Q-interval, in a limited number of points, affected by experimental errors. Furthermore, a theoretical model distribution usually is not available for irradiation effects in such technical steels. All this must be taken into account in selecting the fitting parameters, to obtain plausible distributions and, at the same time, reduce their error band as much as possible.
4. Results and Discussion
The SANS measurements were carried out utilizing the D22 instrument at the Institut Max von Laue-Paul Langevin in Grenoble [
22]. First the samples irradiated to 2.7 dpa at 300 °C and to 8.4 dpa at 300 °C were investigated [
10,
11]; subsequently, the sample irradiated to 16.3 dpa at 250 °C was investigated [
12]. To clarify some uncertainties relating to the utilized un-irradiated reference samples [
12] and to obtain a more homogeneous data set in the same experimental conditions, the two samples irradiated at the higher dose levels were recently measured again, together with other similar ones [
13,
14]. A neutron wavelength of 6 Å and sample-to-detector distances of 2 m and 11 m were selected in order to cover a
Q-interval ranging from 3.0 × 10
−3 Å
−1 to 2.6 × 10
−1 Å
−1, corresponding to sizes 2
R~π/
Q varying between 10 Å and 1000 Å approximately. An external magnetic field of 1 T was applied in the horizontal direction, perpendicular to the neutron beam (see
Figure 2). The SANS cross-sections parallel and perpendicular to the applied magnetic field were determined by selecting on the 2D detector plane sectors 15° wide. Each experiment included the measurement of the same un-irradiated Eurofer97 reference sample, to check that the cross-sections of the irradiated samples, obtained in the different experiments, can be quantitatively compared after calibration into physical units.
Figure 3 shows the nuclear SANS cross-sections of the reference sample as measured in the first experiment [
10] and in the latest one [
13]: they are in good agreement, also considering that SANS data had been reduced by two different programs, namely the one described in Reference [
23] for the first experiment and the one described in Reference [
24] for the latest experiment. The experimental errors on the SANS cross-sections were of a few % in all these experiments.
These experimental results are summarized in the overview of
Figure 4.
The nuclear SANS cross-sections of irradiated and un-irradiated reference samples are shown separately for each irradiation condition in
Figure 5 to appreciate the changes with respect to the reference sample more adequately and also because of the differences in
Q range and cross-sections between the 2.5 dpa irradiated sample and the two others. Similar differences are observed when comparing the nuclear plus magnetic SANS cross-sections of these same samples.
A small but well detectable increase in the SANS cross-section is observed after irradiation to 2.5 dpa. In the same
Q range, for the samples irradiated to 8.4 dpa and 16.3 dpa the increase in SANS cross-section is one order of magnitude higher. Furthermore, the wider
Q range available for the measurements of these two samples shows that for approximately
Q < 10
−2 Å
−1 their cross-sections are nearly coincident with one of the reference samples and all follow a
Q−4 behavior (“Porod law” [
15,
16], see also
Figure 4a), determined by defects with sizes outside the experimental
Q window: this behavior is attributed to carbide precipitates larger than approximately 500 Å, generally not affected by irradiation for such temperatures and dose levels [
25]. As shown in
Figure 4b, for the three irradiated samples the
R(
Q) ratio is close to 2 and within the experimental uncertainties introduced by combining the nuclear and nuclear plus magnetic SANS cross-sections as indicated in Equation (2). The slightly higher
R(
Q) value measured for the sample irradiated to 8.4 dpa around approximately
Q = 2.5 × 10
−2 Å
−1, in correspondence to the small “bump” visible in
Figure 4a and
Figure 5b, could be attributed to the presence of a different kind of defect.
The size and volume distribution functions have been determined assuming that the observed SANS effects are determined by micro-voids as those shown in
Figure 1; therefore, taking a nuclear contrast value of 5.51 × 10
21 cm
−4, a spherical form factor was assumed. In the previous papers [
10,
11,
12,
13,
14], such distributions were obtained introducing up to 10 spline functions in order to fit the whole SANS cross-sections at least in the higher
Q-range and corresponding to 2 m sample-to-detector distance. Furthermore, a wide
Rmin – Rmax range had been selected with
Rmin = 1 Å. This approach yielded defect distributions affected by unphysical oscillations and by a large error band, with consequent difficulties in attempting a metallurgical interpretation: this is particularly evident in Figure 2 of Reference [
14]. On the other hand, recent work carried out on SANS data obtained from other irradiated Eurofer97 samples [
21] has shown that more accurate and significant distributions are obtained reducing the number of splines to a maximum of 7, setting
Rmin to the more realistic value of 3 Å and excluding from the fitting procedure those points clearly affected by the “Porod background” at low
Q’s and by uncertainty on the background level at high
Q’s. A constant background of few units in 10
−3 cm
−1 has also been introduced to improve the fit for the points at the higher
Q values, particularly for the data in
Figure 5c. This way to proceed implies an unavoidable degree of arbitrariness, either in the choice of the fitting parameters or in the selection of the points to be excluded from the fit; however, no theoretical model is currently available for such complex samples, therefore at present only an empirical SANS data analysis seems possible. The data shown in
Figure 5 have been analyzed in this way, determining for each irradiated sample the best-fit distributions obtained with and without the subtraction of the reference sample’s cross-section. As the SANS cross-section (Equation (1)) is governed by the square volume of the defects, volume distributions provide metallurgical information that is more significant with respect to the number of distributions, as shown in previous research [
21]. Therefore, the obtained volume distributions as defined in Equation (5) are presented here below.
For the sample irradiated at 300 °C to 2.7 dpa, a good fit with the experimental SANS cross-section is obtained both with and without the subtraction of the reference sample’s cross-section (
Figure 6a); in both cases, it is necessary to exclude from the fit a few points at low
Q’s, probably partly affected by the “Porod background.” The corresponding distributions are shown in
Figure 6b: subtracting the reference sample yields a mono-disperse distribution of very small voids
(<R> = 4.4 Å) with a volume fraction of 0.001. Considering that interatomic distances in such steels are approximately 3 Å, micro-voids of approximately 10 Å in diameter should be considered as very small vacancy clusters that are close to the experimental resolution limit of the SANS and TEM techniques.
Also for the sample irradiated at 300 °C to 8.4 dpa a good fit is obtained both with and without subtraction of the reference sample’s cross-section (
Figure 7a). The corresponding distributions (
Figure 7b) are very similar, with volume fraction and average radius values around 0.007 and 6.5 Å respectively. A secondary population of defects one order of magnitude larger is also observed after subtraction of the reference sample: it is correlated with the cross-section’s trend in the
Q range approximately 3.5–2 × 10
−2 Å
−1 and its size corresponds to the larger micro-voids shown in
Figure 1 and in Reference [
6]. However, as pointed out above, the
R(
Q) value is significantly higher than 2, suggesting the presence of a different kind of defect.
For the sample irradiated at 250 °C to 16.3 dpa, the subtraction of the reference’s sample cross-section is possible only in a restricted
Q range, where the effect of the irradiation is detected (
Figure 5c), but a good fit is anyhow obtained (
Figure 8a). Similar mono-disperse distributions are obtained (
Figure 8b) with volume fraction and average radius values around 0.004 and 12.9 Å, respectively.
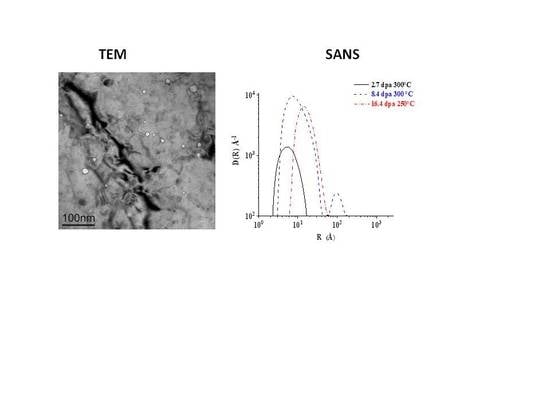
The distributions obtained for these three samples after reference subtraction are compared in
Figure 9;
Table 1 lists the obtained average radii and volume fractions. The uncertainty bands visible in
Figure 6,
Figure 7 and
Figure 8 and the corresponding errors on the values of
Table 1 are smaller than 10%. These errors result from the best fits obtained under the assumptions described here above. An estimate of the uncertainties resulting from different methodological assumptions and choice of the fitting parameters is provided for example by the comparison with the distributions previously obtained for these same samples [
14]. Consistently higher values of volume fraction and lower values of average radii had been obtained with the already mentioned larger error bands and unphysical oscillations (Figure 2 in Reference [
14]): in fact in the previous works, the cross-section considered for the fit was not solely determined by the effect of the irradiation, but partly contaminated by the spurious effects described here above. Furthermore, the previous SANS data analysis lead to some incorrect conclusions about the shape of the distributions, appearing bi-modal as particularly evident in Figure 4 of Reference [
11], with no change in the average radii; however, this result was obtained because spurious effects related to the background noise and asymptotic contribution of large carbide precipitates were included in the fit. On the contrary, genuine information on the irradiation effects is provided by the new distributions presented in this paper, summarized in
Figure 9. They are mono-disperse and the micro-void radius increases with the dose. In fact, after subtraction of the reference samples, an average radius of 4.4 Å is found for 2.7 dpa, 6.6 Å for 8.4 dpa, and 12.9 Å for 16.3 dpa. Furthermore, the previous SANS data analysis did not allow any clear conclusion on the effect of subtracting the reference sample’s cross-section nor a reliable determination of the average radii, while the volume fractions were overestimated. These problems are solved by the new data analysis presented in this paper and summarized in
Table 1.
The obtained results suggest first of all that up to 16.3 dpa only low volume fractions of small micro-voids are produced in Eurofer97 under neutron irradiation at low temperature; this is consistent with resistance to irradiation expected for this steel [
9]. It is difficult to establish clear trends of microstructural damage evolution with dose or temperature, also because only three irradiated samples were investigated—although even for such a limited number a consistent effort was needed for sample transportation and experiment organization, given the high activity of the samples. However, a significant increase of the micro-voids average radius with the dose is observed and, most importantly, well defined mono-disperse distributions are found after subtraction of the reference sample. This is potentially quite useful for modeling purposes of radiation damage evolution in this steel. The secondary population observed in the sample irradiated to 8.4 dpa, consistent with the measured SANS cross-section could be originated by a different kind of defect (see also
Figure 4b) and in this case, the volume distribution should be determined again introducing a model with two different contrast values for two different kinds of defects. No such evidence is provided by the currently available TEM observations [
6].
Additional information on the microstructural evolution in low-temperature neutron irradiated Eurofer97 is obtained comparing the distributions of these samples with the one obtained for a Eurofer97 sample irradiated to 32 dpa at 330 °C at the BOR60 reactor [
13]; also, in this case, the observed SANS effects are tentatively attributed to micro-voids.
Figure 10 shows the volume distribution of this sample re-calculated by the procedure described here above (without reference subtraction) and compared to the distributions shown in
Figure 9 for HFR irradiation at 8.4 dpa and 16.4.
Despite the higher irradiation dose, the obtained average radius (6.5 Å) and volume fraction (0.007) of the BOR60 sample are the same as those found for the 8.4 dpa HFR irradiated sample. It is noted that also in this case, the previous SANS data analysis yielded unclear conclusions concerning the comparison between the HFR and the BOR60 irradiated samples (Figure 6 Reference [
13]). In fact, a more appropriate choice of the fitting parameters provides a well-defined mono-disperse distribution also for the first one. As suggested in Reference [
13], the very low helium production under fast neutron irradiation could partly explain this effect because the helium produced under mixed spectrum plays an important role in stabilizing the micro-voids and promoting their growth. A more systematic investigation of samples irradiated for the same dose and temperature at the two neutron sources would be necessary to come to some conclusions. It is noted that the BOR60 sample also shows a secondary population of very large defects (in addition to a mono-disperse distribution) suggesting that this effect related to the higher irradiation temperature for the higher dose levels; in fact, it was not observed in the sample irradiated to 2.7 dpa at 300 °C, although it was measured in a more limited
Q range.